Глава 2. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
2.1 Зависимые и независимые события. Теоремы сложения и умножения вероятносте.
Событие А называется независимым от события В, если его вероятность не зависит от появления или не появления В, в противном случае событие А называют зависимым от события В.
Вероятность события А, вычисленная в предположении, что событие В произошло, называется условной вероятностью, обозначается 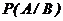 и вычисляется:
и вычисляется:
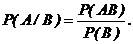 (2.1)
(2.1)
Вероятность появления суммы двух несовместных событий равна сумме вероятностей этих событий
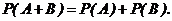 (2.2)
(2.2)
Вероятность появления суммы попарно несовместных событий равна сумме вероятностей этих событий:
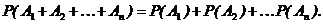 (2.3)
(2.3)
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
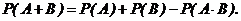 (2.4)
(2.4)
Формула (2.4.) может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий:
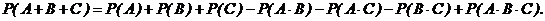 Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
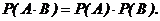 (2.5)
(2.5)
Вероятность появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий: 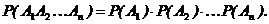
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, при условии, что первое событие произошло:
|
|
|
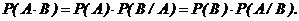 (2.6.).
(2.6.).
Вероятность совместного появления нескольких зависимых событий равна произведению вероятностей одного из них на условные вероятности всех последующих событий, вычисленных в предположении, что все предыдущие события 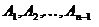 наступили.
наступили.
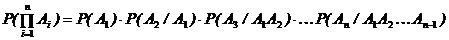
Вероятность наступления события А, состоящего в появлении хотя бы одного из событий 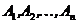 , равна разности между единицей и вероятностью произведения всех противоположных событий
, равна разности между единицей и вероятностью произведения всех противоположных событий 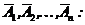
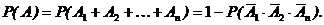 (2.7)
(2.7)
Примечание. Приступая к решению задач на вычисление вероятностей сложных событий, рекомендуется пользоваться следующей схемой:
1) обозначить буквами все события, о которых идет речь в условии задачи;
2) выяснить, совместны или несовместны, зависимы или независимы обозначенные события;
3) выразить сложное событие, о котором идет речь в вопросе задачи, через обозначенные события;
4) выбрать формулу для вычисления нужной вероятности.
Пример 2.1. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что выбранное изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий окажется: а) только одно изделие высшего сорта; б) только два изделия высшего сорта; в) все три изделия высшего сорта.
|
|
|
4Обозначим события:
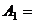 {первое изделие – высшего сорта}
{первое изделие – высшего сорта}
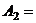 {второе изделие – высшего сорта}
{второе изделие – высшего сорта} 
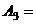 {третье изделие – высшего сорта}
{третье изделие – высшего сорта}
- совместные, независимые;
P(A1)=0,8; P(A2)=0,8; P(A3)=0,8.
а) A = {только одно изделие из трех - высшего сорта}:
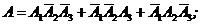
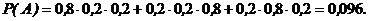
б)B = {только два изделия из трех высшего сорта}:
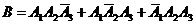 ;
;
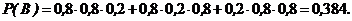
с)С = {все три изделия высшего сорта}:
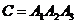 ;
;
 3
3
Пример 2.2.Студент выучил 20 вопросов из 30. Для сдачи зачета необходимо ответить хотя бы на два вопроса из трех заданных. Какова вероятность того, что студент сдаст зачет?
4Обозначим события:
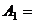 {студент ответил на первый вопрос}
{студент ответил на первый вопрос}
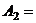 {студент ответил на второй вопрос}
{студент ответил на второй вопрос}
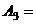 {студент ответил на третий вопрос}
{студент ответил на третий вопрос}
- совместные, зависимые;
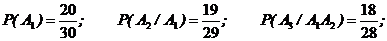
А = {студент сдаст зачет}.
Построим событие А = {студент ответит хотя бы на два вопроса}: 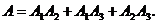
Слагаемые в правой части этого выражения являются совместными, но А можно записать и в виде суммы несовместных слагаемых: 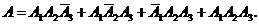
Согласно формул (2.3) и (2.6) будем иметь:
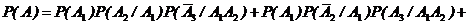
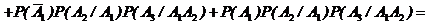
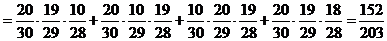 . 3
. 3
Пример 2.3.На трех этапах подготовки прибора к работе вероятности появления независимых друг от друга задержек соответственно равны 0,1; 0,06; 0,05. Какова вероятность того, что прибор будет подготовлен к работе без задержек?
|
|
|
4 Обозначим события:
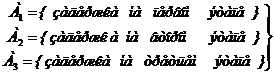 совместны, независимы;
совместны, независимы;
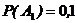 ;
; 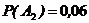 ;
; 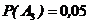 ;
;
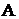 ={подготовка проведена без задержки}.
={подготовка проведена без задержки}.
Тогда 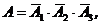 и согласно формуле (2.5)
и согласно формуле (2.5)
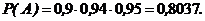 3
3
Пример 2.4. Производится наблюдение за группой состоящей из трех одинаковых объектов. Вероятности обнаружения первого, второго и третьего объектов соответственно равны 0,6 0,8 и 0,7. Найти вероятность того, что обнаружен хотя бы один объект.
4Обозначим события:
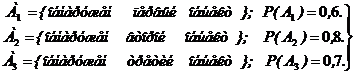 совместны, независимы;
совместны, независимы;
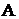 = {обнаружен хотя бы один объект }. Тогда
= {обнаружен хотя бы один объект }. Тогда 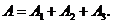
По формуле вычисления вероятности появления хотя бы одного события 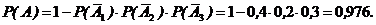 3
3
Пример 2.5.Над изготовлением изделия работают трое рабочих. Качество изделия при передаче следующему рабочему не проверяется. Вероятности того, что первый, второй и третий рабочий допустят брак, соответственно равны 0,2; 0,15; 0,1. Найти вероятность изготовления изделия без брака.
4 Обозначим события: 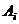 - i –й рабочий допустил брак - совместне, независимые.
- i –й рабочий допустил брак - совместне, независимые.
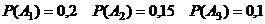 ;
;
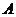 ={получено изделие без брака}.
={получено изделие без брака}.  Тогда
Тогда 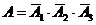 ,
,
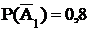 ;
; 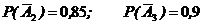 и
и 
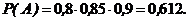 3
3
2.2. Формула полной вероятности. Формулы гипотез (Бейеса).
Пусть событие А может наступить при появлении одного из несовместных событий 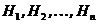 , образующих полную группу и называемых гипотезами. Вероятности гипотез
, образующих полную группу и называемых гипотезами. Вероятности гипотез 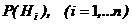 предполагаются известными, причем
предполагаются известными, причем 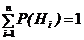 . Тогда вероятность появления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А, вычисленную в предположении, что произошла i – тая гипотеза, т.е.
. Тогда вероятность появления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А, вычисленную в предположении, что произошла i – тая гипотеза, т.е.
|
|
|
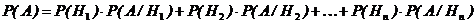 =
=
= 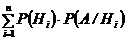 (2.8)
(2.8)
Это равенство называют формулой полной вероятности.
Если событие А произошло, то вероятности гипотез изменятся и могут быть переоценены по формулам Бейеса:
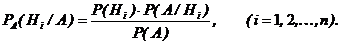 (2.9)
(2.9)
где 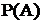 вычисляется в соответствии с формулой (2.8).
вычисляется в соответствии с формулой (2.8).
Пример 2.6. В продажу поступили однотипные изделия с трех заводов. Продукция первого завода содержит 20% изделий с дефектом, второго – 8% и третьего 15%. Какова вероятность приобрести изделие с дефектом, если в магазин поступило 30% изделий первого завода, 50% изделий второго завода и 20% - третьего?
4Обозначим:
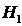 ={изделие произведено первым заводом},
={изделие произведено первым заводом}, 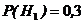 ;
;
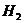 ={изделие произведено вторым заводом},
={изделие произведено вторым заводом}, 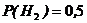 ;
;
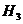 ={изделие произведено третьим заводом},
={изделие произведено третьим заводом}, 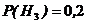 ;
;
А= {купленное изделие имеет дефект}.
Событие А может произойти совместно с одной из гипотез Н 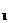 , Н
, Н 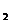 или Н
или Н 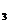 , причем
, причем
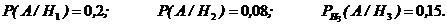
Вероятность события А можно вычислить по формуле полной вероятности:
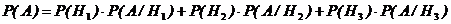 =
=
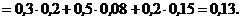 3
3
Пример 2.7. В группе из 12 студентов, пришедших на экзамен, 3 подготовлены отлично, 4 – хорошо, 3 – посредственно и 2 – плохо. В билетах 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный – на 16, посредственно подготовленный – на 10 и плохо подготовленный – на 5. Вычислить вероятность того, что наугад вызванный студент ответит на заданный вопрос.
4Обозначим события:
Н1={вызван отличник} Р (Н1) = 1/4;
Н2={вызван хорошо успевающий} Р (Н2) =1/3;
Н3={вызван посредственно успевающий} Р (Н3) = 1/4;
Н4={вызван плохо успевающий} Р (Н4) = 1/6;
А = {студент ответит на заданный вопрос}.
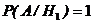 ;
; 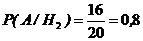 ;
; 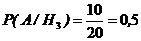 ;
; 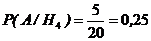 .
.
По формуле полной вероятности находим:
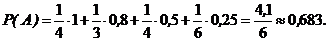 3
3
Пример 2.8. При условии задачи 2.7 определить вероятность того, что студент, ответивший на заданный вопрос, был подготовлен посредственно.
4 Поскольку событие А произошло (студент ответил на заданный вопрос), то вероятность события Н3 изменится и может быть вычислена по формуле Бейеса:
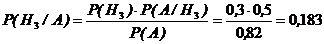 . 3
. 3
Пример 2.9. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55; а ко второму – 0,45. Вероятность того, что изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Изделие при проверке признано стандартным. Найти вероятность того, что его проверил второй товаровед.
4 Обозначим события:
Н1={изделие проверил первый товаровед}, 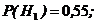
Н2={изделие проверил второй товаровед}, 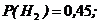
А= {изделие признано стандартным};

Так как событие А произошло, вероятность 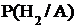 можно вычислить по формуле Бейеса:
можно вычислить по формуле Бейеса: 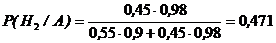 . 3
. 3
Задачи
2.1. Строительная фирма с вероятностью 0,6 может заключить контракт на строительство здания. Согласно контракту, заказчик может произвести оплату одним из 3-х способов: одноразово, равными частями в течение года и с отсрочкой платежа на два года. Вероятности того, что оплата будет произведена первым, вторым или третьим способами, соответственно равны: 0,2; 0,35; 0,4. Определить вероятности того, что фирма: а) получит оплату; б) получит оплату не позже, чем через год; в) не получит оплату.
Ответ: а) 0,95; б) 0,55; в) 0,05.
2.2. Производственная фирма приняла решение о создании инвестиционного фонда. С этой целью она должна в течение трех лет вносить в банк определенные суммы. Вероятности того, что нужные суммы удастся внести в 1-й, 2-й и 3-й год, соответственно равны: 0,6; 0,4; 0,5. Найти вероятность того, что инвестиционный фонд будет создан.
Ответ: 0,12.
2.3. На некотором предприятии 96% изделий признается годными. Из каждой сотни годных изделий в среднем 75 оказывается первого сорта. Найти вероятность того, что изделие, изготовленное на этом предприятии, окажется первого сорта.
Ответ: 0,72.
2.4. По займу ежегодно разыгрываются 6 основных тиражей и один дополнительный, происходящий после основного пятого. Из 100000 серий в каждом основном тираже выигрывают 170 серий, а в каждом дополнительном - 230 серий. Найти вероятность выигрыша на одну облигацию за первые десять лет: а) в основном тираже; б) в дополнительном тираже; в) в каком-либо тираже.
Ответ: а) 0,102; б) 0,023; в) 0,125
2.5. Производившиеся в некотором районе многолетние наблюдения показали, что из 100 000 детей, достигших 10-ти летнего возраста, до 40 лет доживает в среднем 82 277, а до 70 лет - 37977. Найти вероятность того, что если человек достигнет сорокалетнего возраста, то он доживет до 70 лет.
Ответ: 0,4618.
2.6. Из 10 билетов лотереи выигрышных два. Определить вероятность того, что среди взятых наудачу 5 билетов: а) один выигрышный; б) хотя бы один выигрышный.
Ответ: а) 5/9; б) 7/9.
2.7. Рабочий обслуживает 3 станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,9 для второго 0,8 и для третьего 0,85. Найти вероятность того, что в течение часа ни один станок не потребует к себе внимания рабочего.
Ответ: 0,612.
2.8. Вытачивается деталь в виде прямоугольного параллелепипеда. Деталь считается годной, если длина каждого из ребер отклоняется от заданных размеров не более чем на 0,01 мм. Вероятность отклонений, превышающих 0,01 мм, составляет: по длине 0,08; по ширине 0,12; по высоте 0,1 мм. Найти вероятность непригодности детали.
Ответ: 0,271.
2.9. Вероятность того, что изделие некоторого производства удовлетворяет стандарту, равна 0,96. Предлагается упрощенная схема испытаний, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту, и 0,05 для изделий, которые ему не удовлетворяют. Какова вероятность того, что изделие, выдержавшее испытание, удовлетворяет стандарту?
Ответ: 0,9978.
2.10. Монету бросают до тех пор, пока не появится два герба подряд или две решетки. Найти вероятность того, что понадобится не более трех бросков.
Ответ: 3/8.
2.11. Страховая компания установила, что в среднем один из 1000 векселей не подлежит оплате и обязательно является просроченным. Так же известно, что один вексель из 100 подлежащих оплате, просрочен. Компания получила просроченный вексель. Какова вероятность того, что он не подлежит оплате?
Ответ: 0,09.
2.12. На железнодорожную станцию поступает состав из 20 вагонов, направляемых в различные адреса. В первый адрес направляется 5, во второй ‑ 7, а в третий ‑ 8 вагонов соответственно. Вагоны в составе расположены произвольно. Все места вагонов равновероятны. Найти вероятность того, что все вагоны, направляемые в один и тот же адрес, будут стоять рядом.
Ответ: (5!7!8!)/20!.
2.13. В партии из 10 деталей 4 дефектных. Для контроля берут 4. Если среди них окажется более 2 дефектных, то вся партия бракуется. Найти вероятность того, что вся партия будет забракована.
Ответ: 5/42.
2.14. Студент выучил 20 вопросов из 30. Для сдачи зачета необходимо ответить хотя бы на два вопроса из трех заданных. Какова вероятность того, что он сдаст зачет?
Ответ:0,749.
2.15. На полке библиотеки стоят 20 книг. 7 из них – учебники по теории вероятностей. Найти вероятность того, что а) из трех выданных книг не менее двух – учебники по теории вероятностей; б) хотя бы одна выданная книга – учебник по теории вероятностей.
Ответ: а) 0,27; б) 0,025.
2.16.  В лотерее 25 билетов, из которых 6 – выигрышных. Какова вероятность получения выигрыша, имея 3 билета? (Подумайте, что означает выигрыш?)
В лотерее 25 билетов, из которых 6 – выигрышных. Какова вероятность получения выигрыша, имея 3 билета? (Подумайте, что означает выигрыш?)
Ответ: 0, 5787.
2.17. Система, фиксирующая процесс ценообразования, представлена на схеме. Вероятность выхода из строя каждого элемента равна 0,1. Найти вероятности: а) безотказной работы системы; б) выхода .системы из строя.
Ответ: а) 0,975; б) 0,025.
2.18. Пяти радиостанциям разрешено работать на семи радиоволнах. Выбор волны производится случайно. Найти вероятность того, что при работе всех пяти радиостанций будут использованы различные волны.
Ответ: 0,1499.
2.19. Из полного набора костей домино (28) выбирают 5. Найти вероятность того, что среди них будет хотя бы 2 шестерки.
Ответ: 0,3666.
2.20.  Получена партия из восьми изделий одного образца. По данным проверки половины партии, три изделия оказались технически исправными, а одно бракованным. Вычислить вероятность того, что при проверке трех следующих изделий одно из них окажется исправным, а два – бракованными. Предположения о любом количестве бракованных изделий в партии равновозможны.
Получена партия из восьми изделий одного образца. По данным проверки половины партии, три изделия оказались технически исправными, а одно бракованным. Вычислить вероятность того, что при проверке трех следующих изделий одно из них окажется исправным, а два – бракованными. Предположения о любом количестве бракованных изделий в партии равновозможны.
Ответ .0,625.
2.21.  Найти вероятность прохождения сигнала через системы, если вероятность безотказной работы каждого из элементов равна 0,9- для первой схемы и 0,2 – для второй.
Найти вероятность прохождения сигнала через системы, если вероятность безотказной работы каждого из элементов равна 0,9- для первой схемы и 0,2 – для второй.
Ответ: 0,993- для перовой схемы и 0,063 – для второй.
2.22. Детали проходят три операции обработки. Вероятность получения брака на первой операции равна 0,02; на второй – 0,03 и на третьей 0,01. Найти вероятность получения детали без брака после этих трех операций, если получение детали без брака на каждой операции – независимые события.
Ответ: 0,94.
2.23. Из цифр 1, 2, 3, 4, и 5 выбирается одна, а из оставшихся –другая. Найдите вероятность того, что будет выбрана нечетная цифра а) первый раз; б)второй раз; в) оба раза.
Ответ: а) 0,6; б) 0,5; в) 0,3.
2.24. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый и второй вопросы билета, равны 0,9; на третий – 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить: а) на все вопросы; б) хотя бы на два вопроса.
Ответ: а) 0,648; б) 0,953.
2.25. Двое поочередно бросают монету, причем выигрывает тот, у кого раньше появится герб. Определить вероятность выигрыша для каждого игрока.
Ответ: 2/3 ; 1/3.
2.26. Трое поочередно бросают монету, причем выигрывает тот, у кого раньше появится герб. Определить вероятность выигрыша для каждого игрока.
Ответ: 4/7; 2/7; 1/7.
2.27. В жюри из трех человек два члена независимо друг от друга принимают правильное решение с вероятностью 0,8, а третий для принятия решения бросает монету (окончательное решение выносится большинством голосов). С другой стороны, некий судья принимает правильное решение с вероятностью 0,8. Кто с большей вероятностью примет правильное решение: жюри или судья?
Ответ: С одинаковой вероятностью.
2.28. Сколько раз нужно бросить пару игральных костей, чтобы с вероятностью, не меньшей 0,5, можно было надеяться, что хотя бы один раз появится 12 очков?
Ответ: 25.
2.29. Имеются две партии деталей по 12 и 10 штук, причем в каждой партии одна деталь - бракованная. Деталь, взятую наугад из первой партии, переложено во вторую, после чего взята деталь из второй партии. Найти вероятность извлечения бракованного изделия из второй партии.
Ответ: 13/120.
2.30. Для контроля продукции из трех партий деталей взята для испытания одна деталь. Как велика вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованные, а в двух других ‑ все доброкачественные?
Ответ: 2/9.
2.31. Характеристика материала, взятого для изготовления продукции, может находиться в шести различных интервалах с вероятностями: 0,09; 0,16; 0,25; 0,25; 0,16 и 0,9. В зависимости от свойств материала вероятности получения первосортной продукции равны соответственно 0,2; 0,3; 0,4; 0,4; 0,3 и 0,2. Определить вероятность получения первосортной продукции.
Ответ: 0,332.
2.32. Для посева заготовлены семена пшеницы первого сорта, смешанные с небольшим количеством примесей зерен второго, третьего и четвертого сортов. Вероятности того, что наудачу взятое зерно окажется того или иного сорта известны и равны соответственно: 1 сорта ‑ 0,96; 2 сорта ‑ 0,01; 3 сорта ‑ 0,02; 4 сорта ‑ 0,01. Вероятность того, что из зерна вырастит колос, содержащий не менее 50 зерен, равна: 0,50 для зерна 1-го сорта, 0,15 для зерна 2-го сорта, 0,20 для зерна 3-го сорта и 0,05 для зерна 4-го сорта. Найти вероятность того, что колос будет иметь не менее 50 зерен.
Ответ: 0,486.
2.33. Вероятность того, что в некотором производстве изделие удовлетворяет стандарту, равна 0,96. Предлагается упрощенная схема испытаний, которая для изделий, удовлетворяющих стандарту, дает положительный результат с вероятностью 0,98, а для изделий ему не удовлетворяющих ‑ лишь с вероятностью 0,05. Какова вероятность того, что изделие, дважды выдержавшее упрощенное испытание, удовлетворяет стандарту?
Ответ: 0,9428.
2.34. Из первой урны взят шар и опущен во вторую, в которой есть 1 белый и 1 черный шары. После этого из второй урны наугад извлечен 1 шар. Какова вероятность, что он белый?
Ответ: 0,5.
2.35. Из первой урны, содержащей 1 шар, взят шар и опущен во вторую, в которой есть 1 белый и 1 черный шары. После этого из второй урны наугад извлечен 1 шар. Он оказался белым. Какого цвета шар был в первой урне наиболее вероятно?
Ответ: Белый (р=0,5).
2.36. При переливании крови надо учитывать группу крови донора и больного. Человеку, имеющему четвертую группу крови можно перелить кровь любой группы; человеку со второй или с третьей группой крови можно перелить кровь либо той же группы, либо первой; человеку с первой группой можно перелить только кровь первой группы. Среди населения 33,7% имеют первую, 37,5% - вторую, 20,9% - третью и 7,9% - четвертую группу крови. а) Найдите вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора.
Ответ : 0,574.
2.37. Агентство по страхованию автомобилей разделяет водителей по трем классам: класс 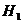 (мало рискует), класс
(мало рискует), класс 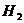 (рискует средне), класс
(рискует средне), класс 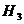 (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежит к классу
(рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежит к классу 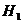 , 50% - к классу
, 50% - к классу 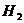 и 20% - к классу
и 20% - к классу 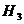 . Вероятность того, что в течение года водитель класса
. Вероятность того, что в течение года водитель класса 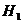 хотя бы в одну аварию равна 0,01, для водителя класса
хотя бы в одну аварию равна 0,01, для водителя класса 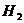 эта вероятность равна 0,02, а для водителя класса
эта вероятность равна 0,02, а для водителя класса 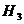 - 0,08. Водитель страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу
- 0,08. Водитель страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу 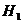 ? К классам
? К классам 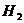 или
или 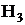 ?
?
Ответ: 0,103; 0,35; 0,55.
2.38. Из двух близнецов первым родился мальчик. Какова вероятность того, что вторым родится тоже мальчик, если среди близнецов вероятность рождения 2 мальчиков и 2 девочек соответственно равна p и q, а для разнополых близнецов вероятность родиться первым для обоих полов одинакова?
Ответ: 2р/( 1 + р – q ).
2.39. Известно, что 96% выпускаемой заводом продукции отвечает стандарту. Упрощенная схема контроля признает годной стандартную продукцию с вероятностью 0,98 и нестандартную с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль отвечает стандарту.
Ответ: 0,998.
2.41. В игре в кости необходимо было для выигрыша получить при бросании трех игральных костей сумму очков, превосходящую 10. Найти вероятности: а) выпадения 11 очков; б) выигрыша.
Ответ: а) 0,125; б) 0,5.
2.42. На фирме работают 8 аудиторов, из которых 3 – высокой квалификации и 5 программистов, из которых 2 – высокой квалификации. В командировку отправляют 3 аудиторов и 2 программистов. Какова вероятность того, что в этой группе окажутся, по крайней мере, 1 аудитор высокой квалификации и хотя бы 1 программист высокой квалификации, если каждый специалист имеет равные шансы поехать в командировку?
Ответ: 0,329
2.43. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе – 0,9 и в третье – 0,8. Найти вероятность следующих событий: а) только одно отделение получит газеты вовремя; б) хотя бы одно отделение получит газеты с опозданием.
Ответ: а) 0,032, б) 0,316.
2.44. На связке 5 ключей. К замку подходит только один ключ. Найти вероятность того, что потребуется не более двух попыток, чтобы открыть замок, если опробованный ключ в дальнейших испытаниях не участвует.
Ответ: 0,4.
2.45. Брак в продукции завода вследствие дефекта А составляет 4%, а вследствие дефекта В– 3,5%. Годная продукция завода 95%. Найти вероятность того, что: а) среди продукции не имеющей дефекта А встретится дефект В; б) среди продукции, забракованной по дефекту А встретится дефект В.
Ответ: а) 0,0104; б) 0,625.
2.46. Пакеты акций, имеющихся на рынке ценных бумаг, могут дать доход владельцу с вероятностью 0,5 для каждого пакета. Сколько пакетов акций различных фирм нужно приобрести, чтобы с вероятностью, не меньшей 0,96875, можно было ожидать доход хотя бы по одному пакету акций?
Ответ: Не менее 5 пакетов.
2.47. Из n экзаменационных билетов студент подготовил только m (m<n). В каком случае вероятность вытащить «хороший» для него билет выше: когда он берет наудачу билет первым или вторым, … , k-м по счету среди сдающих экзамен?
Ответ: вероятность одинакова: 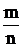 .
.
2.48. Для малого предприятия вероятность обанкротиться за время t равна 0,2. Найти вероятность того, что из 8 малых предприятий за время t сохранятся: а) два: б) более двух?
Ответ: а) 0,717; б) 0,999.
Дата добавления: 2018-05-13; просмотров: 4320; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
