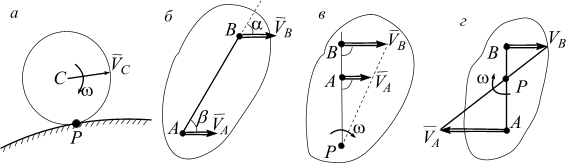
Частные случаи вычисления МЦС
Рассмотрим частные случаи вычисления точки МЦС.
1. Если плоское движение осуществляется путем качения без скольжения однородного цилиндрического тела по поверхности другого тела, причем второе тело неподвижно, то точка касания Р имеет в данный момент времени скорость, равную нулю, следовательно, является МЦС (рис. 2.32, а), т. е. тело мгновенно вращается относительно точки касания Р. Пример– качение колеса по рельсу.
|
|
Рис. 2.32
2. Если скорости точек А и В тела параллельны друг другу, причем линия АВ не перпендикулярна к 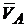 и
и 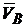 (рис. 2.32, б), то восстанавливая перпендикуляры к скоростям, выясним, что точка МЦС находится в бесконечности, тогда
(рис. 2.32, б), то восстанавливая перпендикуляры к скоростям, выясним, что точка МЦС находится в бесконечности, тогда 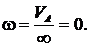 Из общей теоремы кинематики имеем
Из общей теоремы кинематики имеем 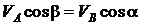 (
( 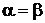 ), тогда VВ = VА. Следовательно, скорости всех точек тела в данный момент равны между собой по модулю и по направлению, т. е. тело движется мгновенно поступательно. Примгновенно поступательном движении угловая скорость тела равна нулю, угловое ускорение не всегда равно нулю.
), тогда VВ = VА. Следовательно, скорости всех точек тела в данный момент равны между собой по модулю и по направлению, т. е. тело движется мгновенно поступательно. Примгновенно поступательном движении угловая скорость тела равна нулю, угловое ускорение не всегда равно нулю.
3. Если скорости точек А и В тела параллельны друг другу и при этом 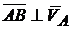 , то положение точки МЦС определяется построениями, показанными на рис. 2.32, в, г; тело имеет мгновенно вращательное движение вокруг точки МЦС(точка Р). Известно, что модули скоростей точек тела пропорциональны их расстояниям от точки МЦС, т. е.
, то положение точки МЦС определяется построениями, показанными на рис. 2.32, в, г; тело имеет мгновенно вращательное движение вокруг точки МЦС(точка Р). Известно, что модули скоростей точек тела пропорциональны их расстояниям от точки МЦС, т. е.
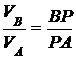 .
.
4. Если на перпендикуляре к вектору скорости есть точка, скорость в которой равна нулю, то эта точка будет точкой МЦС.
|
|
|
|
| Рис. 2.33 |
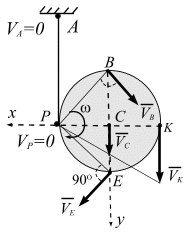
На рис. 2.33 приведен пример маятника Максвелла – на диск радиусом  намотана нерастяжимая нить, конец которой закреплен в точке А. Свяжем декартову систему координат
намотана нерастяжимая нить, конец которой закреплен в точке А. Свяжем декартову систему координат  с центром диска. Скорость в точке С параллельна оси
с центром диска. Скорость в точке С параллельна оси  . На оси
. На оси 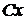 скорость в точке
скорость в точке  равна нулю (
равна нулю ( 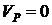 ). Точка Р МЦС. Модули скоростей точек диска связаны соотношением
). Точка Р МЦС. Модули скоростей точек диска связаны соотношением
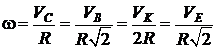 .
.
Теорема. Ускорение какой-либо точки тела при его плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении тела вокруг полюса.
Если А – полюс, то ускорение любой точки М плоской фигуры по теореме
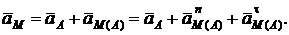
здесь 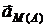 – ускорение точки М в её вращении вместе с фигурой вокруг полюса А (рис. 2.34, а, б), которое, в свою очередь, складывается из касательного и нормального ускорений.
– ускорение точки М в её вращении вместе с фигурой вокруг полюса А (рис. 2.34, а, б), которое, в свою очередь, складывается из касательного и нормального ускорений.
Касательная составляющая ускорения (рис. 2.34, а, в) направлена ^ АМ в сторону дуговой стрелки  и равна
и равна 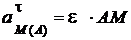
Нормальная составляющая ускорения (рис. 2.34, а, в) направлена по нормали, т. е. по АМ к полюсу А, и равна 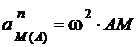 .
.
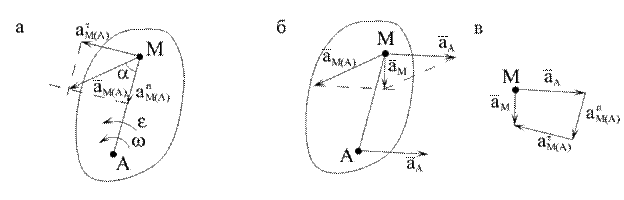
Рис. 2.34
Содержание контрольных работ для студентов на тему «плоское движение твердого тела» дано в приложении (контрольная работа 2, задачи 1 и 2).
Пример 2.7.
Исходные данные: кривошип ОА длиной 60 см вращается ускоренно относительно оси О и приводит в движение ролик 1 радиусом  см, который катится без скольжения по неподвижному колесу 2 (рис. 2.35). Параметры вращения кривошипа в данный момент времени
см, который катится без скольжения по неподвижному колесу 2 (рис. 2.35). Параметры вращения кривошипа в данный момент времени 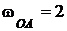 с-1,
с-1,
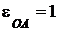 с-2.
с-2.
|
|
|
Требуется: определить угловую скорость  и угловое ускорение
и угловое ускорение 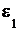 ролика, вычислить скорость и ускорение точки В, находящейся на ролике на расстоянии 10 см от точки А.
ролика, вычислить скорость и ускорение точки В, находящейся на ролике на расстоянии 10 см от точки А.
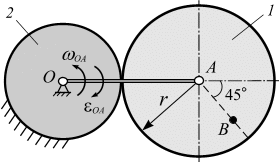
Рис. 2.35
Решение. Кривошип ОА совершает вращательное движение относительно оси, проходящей через неподвижный центр О. Скорость и ускорение точки А кривошипа вычисляют по формулам:
 см/с;
см/с;
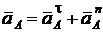 .
.
Подвижный ролик движется плоскопараллельно. Вычислим  и
и 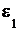 подвижного ролика. Плоское движение ролика можно привести к мгновенно-вращательному движению относительно мгновенного центра скоростей (МЦС), этим центром является точка касания Р (рис. 2.36).
подвижного ролика. Плоское движение ролика можно привести к мгновенно-вращательному движению относительно мгновенного центра скоростей (МЦС), этим центром является точка касания Р (рис. 2.36).
Запишем уравнение связи между движениями кривошипа и ролика. Точка А одновременно принадлежит кривошипу ОА и ролику 1. Следовательно, перемещение точки А:
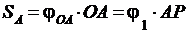 , т. е.
, т. е. 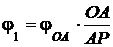 .
.
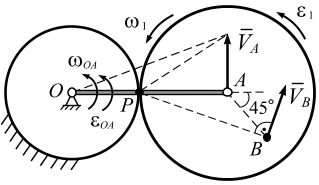
Рис. 2.36
Угловая скорость и угловое ускорение ролика 1 тогда вычисляются:
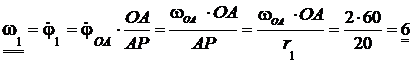 с-1;
с-1;
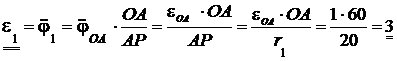 с-2.
с-2.
Угол вращения ролика относительно точки Р (точка МЦС) совпадает с углом вращения кривошипа (рис. 2.36). Направления вращения  и
и 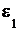 ролика 1 совпадают, отмечаем их дуговыми стрелками; следовательно, движение ролика 1 является ускоренным, как и кривошипа ОА.
ролика 1 совпадают, отмечаем их дуговыми стрелками; следовательно, движение ролика 1 является ускоренным, как и кривошипа ОА.
|
|
|
Скорость точки В.
Точка В находится на ролике 1, следовательно, её скорость определяется как скорость точки, вращающейся вокруг МЦС, т. е. точки Р:
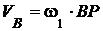 .
.
Из геометрии задачи определим по теореме косинусов расстояние ВР:

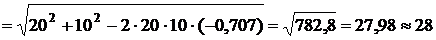 см.
см.
Тогда скорость точки В:
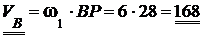 см/с.
см/с.
Вектор 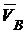 перпендикулярен отрезку ВР и направлен в сторону вращения
перпендикулярен отрезку ВР и направлен в сторону вращения  ролика (рис. 2.36).
ролика (рис. 2.36).
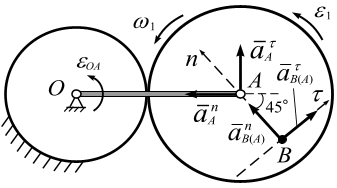
1. Ускорение точки В.
| 
| ||
|
а б Рис. 2.37
| |||
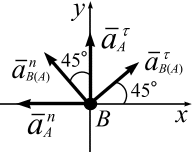
Ускорение точки В складывается из ускорения полюса и ускорения точки В при её вращении вместе с роликом вокруг этого полюса. За полюс примем точку А, т. к. её ускорение известно.
Тогда ускорение точки В запишется (рис. 2.37, а)
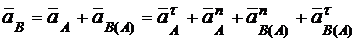 .
.
Здесь:
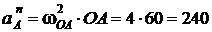 см/с2 - нормальная составляющая ускорения полюса, направлена от точки А к центру О;
см/с2 - нормальная составляющая ускорения полюса, направлена от точки А к центру О;
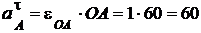 см/с2 - касательная составляющая ускорения полюса, направлена перпендикулярно
см/с2 - касательная составляющая ускорения полюса, направлена перпендикулярно 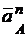 в сторону углового ускорения кривошипа ОА -
в сторону углового ускорения кривошипа ОА - 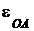 ;
;
|
|
|
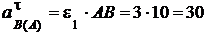 см/с2 - ускорения точки В при её вращении относительно полюса А; вектор
см/с2 - ускорения точки В при её вращении относительно полюса А; вектор 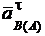 перпендикулярен АВ и направлен в сторону дуговой стрелки
перпендикулярен АВ и направлен в сторону дуговой стрелки 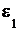 ;
;
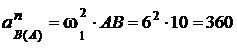 см/с2, вектор
см/с2, вектор 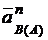 направлен по отрезку АВ от точки В к точке А.
направлен по отрезку АВ от точки В к точке А.
Выражение для расчета ускорения точки В записано в векторной форме. Для аналитических вычислений необходимо спроецировать это векторное равенство на две оси координат, тогда теорема примет вид
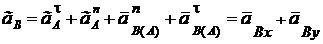 , где
, где
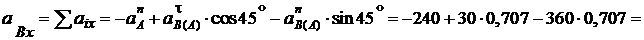
= – 473,31 см/с2;
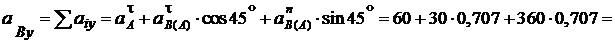
= 335,73 см/с2.
Модуль ускорения точки В вычислим по формуле:
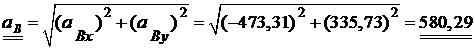 см/с2.
см/с2.
Для определения направления вектора полного ускорения точки В строится параллелограмм на его проекциях 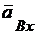 и
и 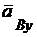 , диагональ этого параллелограмма и будет вектором ускорения точки В.
, диагональ этого параллелограмма и будет вектором ускорения точки В.
Ответ: 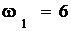 с-1,
с-1,  с-2;
с-2; 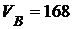 см/с;
см/с; 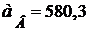 см/с2.
см/с2.
Пример 2.8.
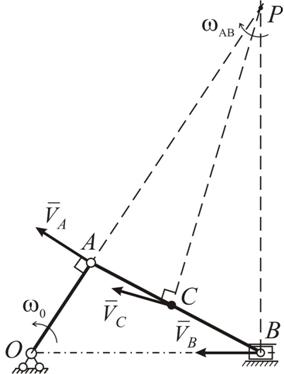
В кривошипно-шатунном механизме кривошип ОА вращается замедленно относительно центра О с угловой скоростью 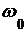 и угловым ускорением
и угловым ускорением 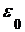 (рис. 2.38) и приводит в движение шатун АВ.
(рис. 2.38) и приводит в движение шатун АВ.
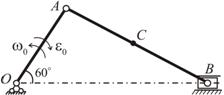
Рис. 2.38
Исходные данные:ОА = 35 см; АС = 40 см; w0= 4 с-1; e0 = 8 с-2; Ð(ОАВ) = 900.
Для заданного положения механизма вычислить:
1. скорости точек А, В, С и угловую скорость шатуна АВ;
2. ускорения точек А, В, С и угловое ускорение шатуна АВ.
Решение
В кривошипно-шатунном механизмекривошип ОА вращается относительно центра О, шатун АВ движется плоскопараллельно, ползун В движется поступательно.
1. Скорости точек и угловая скорость шатуна.
Точка А одновременно принадлежит и кривошипу ОА, и шатуну АВ. Рассматривая вращение кривошипа, скорость точки А рассчитываем по формуле
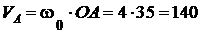 см/с.
см/с.
Вектор скорости  перпендикулярен кривошипу ОА и направлен в сторону угловой скорости кривошипа (рис. 2.39).
перпендикулярен кривошипу ОА и направлен в сторону угловой скорости кривошипа (рис. 2.39).
| ||
| Рис. 2.39 |
Рассмотрим движение шатуна АВ. Заменим плоское движение шатуна АВ мгновенно-вращательным относительно мгновенного центра скоростей (МЦС). Вектор скорости точки В шатуна направлен вдоль направляющих ползуна, в данном случае - по горизонтали. Для нахождения МЦС восстановим перпендикуляры к построенным векторам скоростей  и
и 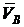 , на их пересечении будет находиться МЦС шатуна - точка Р (рис. 2.39).
, на их пересечении будет находиться МЦС шатуна - точка Р (рис. 2.39).
Направление мгновенного вращения шатуна АВ вокруг МЦС - 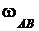 - определяем по направлению вращения вектора
- определяем по направлению вращения вектора 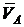 относительно точки Р.
относительно точки Р.
Величина угловой скорости шатуна и скорости точек рассчитывается из выражения:
 .
.
Если положение кривошипно-шатунного механизма фиксировано и начерчено в масштабе, то расстояния ВР и СР измеряются с чертежа линейкой. В общем случае рассматривают геометрию задачи (рис. 2.39).
Рассмотрим треугольники ОАВ и ОРВ:
из 
 см;
см;
из 
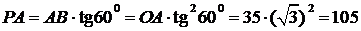 см,
см,
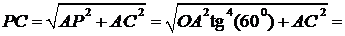
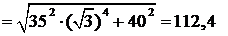 см.
см.
Тогда
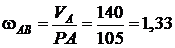 с-1;
с-1;
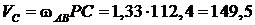 см/с.
см/с.
Вектор скорости  перпендикулярен отрезку РС и направлен в сторону мгновенного вращения шатуна
перпендикулярен отрезку РС и направлен в сторону мгновенного вращения шатуна 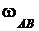 (рис. 2.39).
(рис. 2.39).
Скорость точки В можно вычислить из выражения 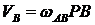 (для этого надо определить РВ), или удобнее воспользоваться первым следствием теоремы о скорости точки плоской фигуры: проекции скоростей точек А и В на прямую (АВ) равны:
(для этого надо определить РВ), или удобнее воспользоваться первым следствием теоремы о скорости точки плоской фигуры: проекции скоростей точек А и В на прямую (АВ) равны:
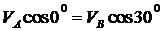 ,
,
тогда  см/с.
см/с.
2. Ускорения точек и угловое ускорение шатуна.
Определим ускорение точки А. Так как движение кривошипа ОА вращательное, то

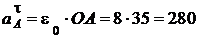 см/с2;
см/с2;
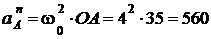 см/с2;
см/с2;
 см/с2.
см/с2.
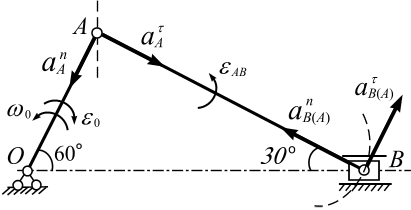
Рассчитываем ускорение точки В ползуна. Для этого рассмотрим её в движении с шатуном АВ. Так как ускорение точки А уже найдено, то принимаем точку А за полюс, тогда по теореме
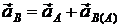 ,
,
или 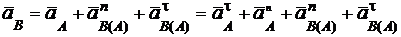 ,
,
здесь (рис. 2.40, а): вектор 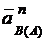 направлен по шатуну АВ от точки В к точке А; вектор
направлен по шатуну АВ от точки В к точке А; вектор 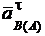 располагаем перпендикулярно шатуну АВ (направление выбираем произвольно, т. к. направление eАВ пока неизвестно):
располагаем перпендикулярно шатуну АВ (направление выбираем произвольно, т. к. направление eАВ пока неизвестно):
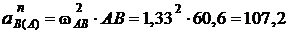 см/с2,
см/с2,
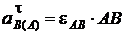 .
.
Прикладываем векторы 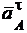 ,
, 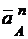 ,
,  ,
, 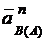 к точке В (рис. 2.40, б).
к точке В (рис. 2.40, б).
| 
|
а б
Рис. 2.40
Ускорение точки В определяется векторным уравнением:
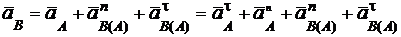 . (а)
. (а)
Таким образом, получили векторное равенство с двумя неизвестными:  и
и 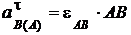 .
.
Вычислить  и
и 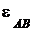 можно двумя способами - аналитическим и геометрическим. Рассмотрим каждый из указанных способов.
можно двумя способами - аналитическим и геометрическим. Рассмотрим каждый из указанных способов.
Аналитический способ. Начало декартовой системы координат совместим с точкой В, одну из осей выбираем перпендикулярно одной из неизвестных, например, ось 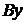 перпендикулярна оси направляющих ползуна (т. е.
перпендикулярна оси направляющих ползуна (т. е. 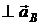 ), тогда ось
), тогда ось 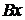 – вдоль направляющих ползуна (рис. 2.40, б). Вектор ускорения ползуна
– вдоль направляющих ползуна (рис. 2.40, б). Вектор ускорения ползуна 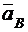 направлен вдоль оси
направлен вдоль оси 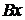 , поэтому проекция вектора
, поэтому проекция вектора 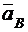 на ось
на ось 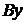 равна нулю. Из (а) получаем:
равна нулю. Из (а) получаем:
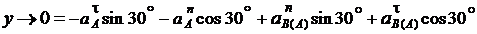 ;
;
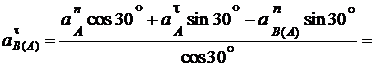
 см/с2;
см/с2;
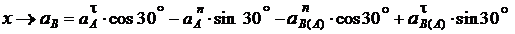
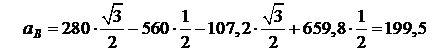 см/с2.
см/с2.
Знаки (+) у 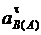 и аВ означают, что направления этих векторов, указанные на рис. 2.40, верны.
и аВ означают, что направления этих векторов, указанные на рис. 2.40, верны.
Вычисляем угловое ускорение шатуна:
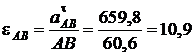 с-2,
с-2,
направление 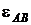 определяется вращением вектора
определяется вращением вектора 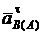 относительно полюса А, т. е. получаем против хода часовой стрелки (рис. 2.40, а).
относительно полюса А, т. е. получаем против хода часовой стрелки (рис. 2.40, а).
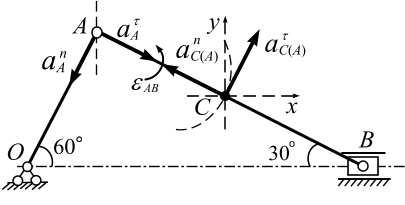
Вычислим ускорение точки С (рис. 2.41).
По теореме ускорение точки С:
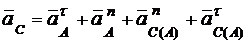 , (б)
, (б)
здесь (рис. 2.41, а): вектор 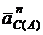 направлен по шатуну АВ от точки С к точке А; вектор
направлен по шатуну АВ от точки С к точке А; вектор 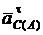 перпендикулярно шатуну АВ по найденному направлению eАВ вокруг полюса А.
перпендикулярно шатуну АВ по найденному направлению eАВ вокруг полюса А.
 (см/с2),
(см/с2),
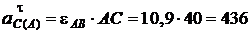 (см/с2).
(см/с2).
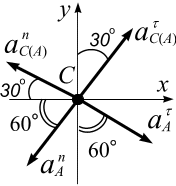
Сводим вектора 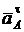 ,
, 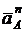 ,
, 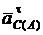 ,
,  в точку С (рис. 2.41 б).
в точку С (рис. 2.41 б).
| 
|
а б
Рис. 1.41
Спроецируем записанное векторное равенство (б) на оси  и Сy
и Сy
(рис. 2.41, б):

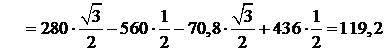 см/с2;
см/с2;
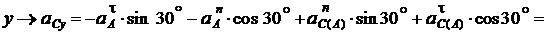
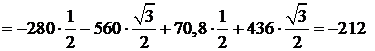 см/с2.
см/с2.
Модуль ускорения точки С:
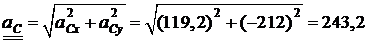 см/с2.
см/с2.
Ответ: 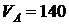 см/с;
см/с; 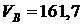 см/с;
см/с;  см/с;ωАВ = 1,33 с-1;
см/с;ωАВ = 1,33 с-1;
аА = 626,1 см/с2; аВ = 199,5 см/с2; аС = 243,2 см/с2; eАВ = 10,9 с-2.
СТАТИКА
Основные элементы статики
Сила ( 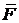 ) – векторная величина (рис. 3.1). Под действием силы тело
) – векторная величина (рис. 3.1). Под действием силы тело
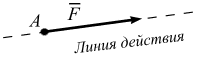
| совершает движение. Сила характеризуется величиной (модулем), направлением (линией действия) и точкой приложения А (рис. 3.1). Одно из важнейших свойств силы – сила скользящий вектор, т. е. действие силы на твердое тело не изменится от переноса вектора силы вдоль своей линии действия. |
| Рис. 3.1 |
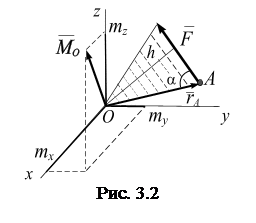 Моментом силы
Моментом силы 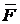 относительно центра О называется вектор
относительно центра О называется вектор  , равный векторному произведению радиуса вектора
, равный векторному произведению радиуса вектора 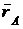 , соединяющего центр О с точкой приложения силы А исилы
, соединяющего центр О с точкой приложения силы А исилы 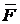 :
:
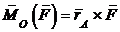 [Н∙м]. (3.1)
[Н∙м]. (3.1)
Вычислим модуль 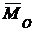 :
:
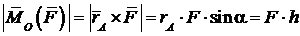 ,
,
здесь 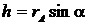 .
.
Пусть 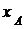 ,
, 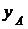 ,
, 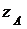 – координаты радиус-вектора
– координаты радиус-вектора 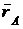 ;
; 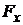 ,
, 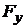 ,
, 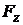 – координаты силы
– координаты силы 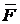 ,тогда(рис. 3.2)
,тогда(рис. 3.2)
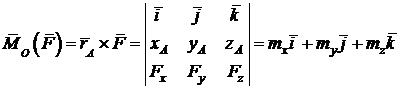 ,
,
|
| Рис. 3.3 |
здесь
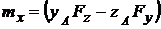 ;
; 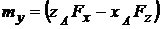 ;
;
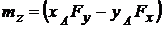 . (3.2)
. (3.2)
Модуль момента 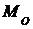 , если известны
, если известны 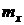 ,
, 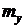 и
и 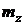 ,
,
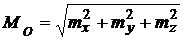 . (3.3)
. (3.3)
Направление вектора 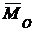 определяется направляющими косинусами (рис. 3.3).
определяется направляющими косинусами (рис. 3.3).
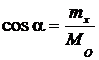 ,
, 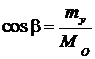 ,
,  . (3.4)
. (3.4)
Проекции вектора 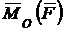 на оси координат
на оси координат  –-
–- 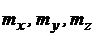 , называют моментами силы
, называют моментами силы 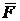 относительно осей
относительно осей 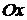 ,
, 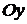 ,
, 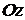 соответственно.
соответственно.
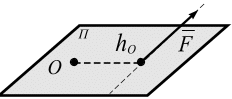
Для плоской системы сил моментом силы относительно моментной точки О называют величину, равную произведению силы F на плечо h, взятому с соответствующим знаком(рис. 3.4)
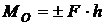 .
.
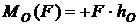
| 
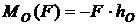
| ||
| а б Рис. 3.4 | |||
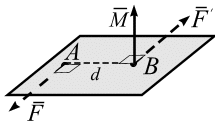
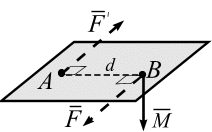
Пара сил. Система сил  , состоящая из двух параллельных сил, равных по модулю, направленных в противоположные стороны и не лежащих на одной линии действия, называется парой сил (рис. 3.5).
, состоящая из двух параллельных сил, равных по модулю, направленных в противоположные стороны и не лежащих на одной линии действия, называется парой сил (рис. 3.5).
Кратчайшее расстояние между линиями действия пары (d) называется плечом пары (рис. 3.5). Пара сил не имеет равнодействующей. Плоскость, проходящая через векторы пары сил, называется плоскостью действия пар. Момент пары сил является вектором, равным
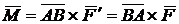 . (3.5)
. (3.5)
Модуль пары сил соответствует площади параллелограмма, построенного на векторах пары
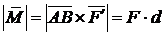 .
.
Момент пары – свободный вектор (может быть приложен к любой точке).
Модуль момента парысил 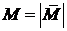 положительный, когда пара стремится повернуть тело против часовой стрелки (рис. 3.5, а), и отрицательный – по ходу часовой стрелки (рис. 3.5 б).
положительный, когда пара стремится повернуть тело против часовой стрелки (рис. 3.5, а), и отрицательный – по ходу часовой стрелки (рис. 3.5 б).
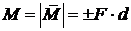 . (3.6)
. (3.6)
| 
| ||
| а б Рис.3.5 | |||
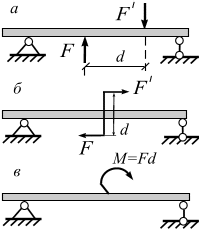
На практике пару сил (рис. 3.6, а) изображают или в виде двух параллельных сил (рис. 3.6, б), или дуговой стрелкой по направлению вращения пары (рис. 3.6, в).
|
| Рис. 3.6 |
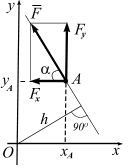
Теорема Вариньона о моменте равнодействующей (для плоской системы сил): если рассматриваемая плоская система сил приводится к равнодействующей, то момент этой равнодействующей относительно какой-либо точки равен алгебраической сумме моментов всех сил данной системы относительно самой точки.
|
| Рис. 3.7 |
Применим теорему Вариньона для случая на рис. 3.7. Момент силы 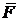 относительно точки О можно определить как
относительно точки О можно определить как 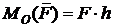 , или воспользоваться теоремой. Так как сила
, или воспользоваться теоремой. Так как сила 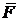 является равнодействующей для системы сил (
является равнодействующей для системы сил ( 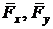 ), то
), то
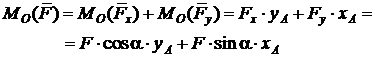
Связи и их реакции
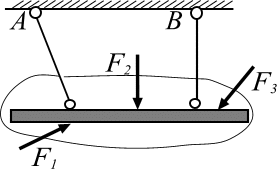
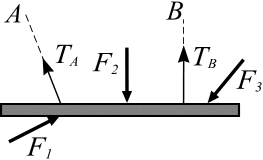
Гибкая невесомая нерастяжимая нить. Невесомый стержень, шарнирно закрепленный по концам.Связь в виде гибкой невесомой нерастяжимой нити (троса, каната и т. д.) или невесомого стержня, шарнирно закрепленного по концам (рис. 3.8, а), не дает телу удаляться от точек подвеса в единственном направлении – вдоль нити или стержня. Выделим замкнутой кривой тело, равновесие которого определяем, отбросим гибкие связи и заменим их действие силами реакций связей (  и
и  ), направим силы реакций связей вдоль нитей (стержня) к точкам ее (его) подвеса (рис. 3.8, б).
), направим силы реакций связей вдоль нитей (стержня) к точкам ее (его) подвеса (рис. 3.8, б).
| 
|
а б
Рис. 3.8
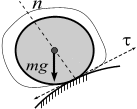
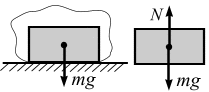
Гладкая поверхность (плоскость) или опора. Гладкая поверхность не дает телу перемещаться только в направлении общей нормали к поверхностям соприкасающихся тел в точке их касания (рис. 3.9, а, б). Выделим замкнутой кривой тело, равновесие которого определяем (рис. 3.9, а), отбросим связь (поверхность) и заменим ее действие силой реакции связи ( 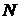 ), которая направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке (рис. 3.9, б). В результате на тело будут действовать две силы – вес тела
), которая направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке (рис. 3.9, б). В результате на тело будут действовать две силы – вес тела  и реакция опоры
и реакция опоры 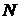 .
.
| 
|
а б
Рис. 3.9
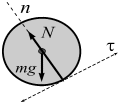
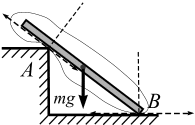
Когда одно из соприкасающихся тел касается другого тела в точке (рис. 3.10), то реакция поверхности направлена по нормали к другой поверхности.
| 
|
а б
Рис. 3.10
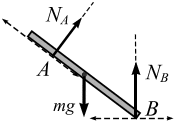
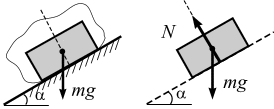
Когда одно из тел лежит на поверхности другого тела (рис. 3.11, а, б), то реакция поверхности направлена по нормали к другой поверхности и проходит через точку центра тяжести тела.
| 
|
а б
Рис.3.11
| Шарнирное соединение, или шарнир,представляет собой устройство (С), связывающее два тела А и В (рис. 3.12, а) и позволяющее телам поворачиваться в плоскости вокруг оси, перпендикулярной этой плоскости. Осевая линия будет осью шарнира. Шарнирное соединение накладывает 2 связи. Следовательно, выделяя тела А и В (разрезая шарнир), | а | 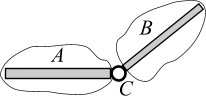
|
| б | 
| |
| Рис. 3.12
| ||
действие связи заменяют реакциями связи  слева от сечения и
слева от сечения и  справа от сечения С, равных по модулю и противоположных по направлению (рис. 3.12, б).
справа от сечения С, равных по модулю и противоположных по направлению (рис. 3.12, б).
| 
| 
|
| а б в Рис. 3.13 | ||
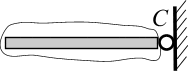
Если балка соединена с гладкой поверхностью шарниром (рис. 3.13, а), то, отбрасывая связь, принято заменять ее реакцией 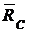 (рис. 3.13, б), которую можно раскладывать на два нормальных направления: горизонтальное
(рис. 3.13, б), которую можно раскладывать на два нормальных направления: горизонтальное  и вертикальное
и вертикальное  , рис. 3.13, в. Тогда:
, рис. 3.13, в. Тогда:  ,
, 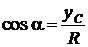 .
.
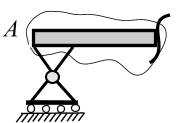
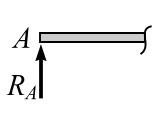
Шарнирно-подвижная опора. Эта опора (рис. 3.14, а) допускает перемещение тела, опертого на эту опору, в направлении, параллельном опорной плоскости, и вращение тела в плоскости относительно шарнира. В строительной документации такую опору принято изображать в виде короткого стержня (рис. 3.14, б) с шарнирами на концах (опорная связь). Реакция опоры 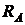 направлена перпендикулярно опорной поверхности
направлена перпендикулярно опорной поверхности
(рис.3.14, в).
| 
| 
|
| а б в Рис. 3.14 | ||
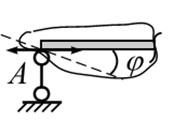
Шарнирно-неподвижная опора.Эта опора (рис. 3.15, а) допускает вращение тела, опертого на эту опору в плоскости, относительно шарнира и не допускает линейных перемещений. Линия действия реакции опоры проходит через ось шарнира под углом 
(рис. 3.15, б).
| а | 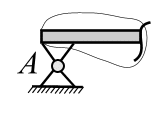
| б | 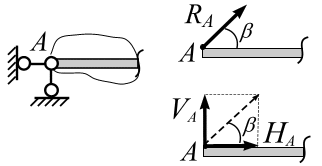
|
| а б в
Рис. 3.15 | |||
Реакция этой опоры содержит две неизвестные – модуль 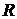 и угол
и угол  . На практике часто, но не всегда, принято раскладывать
. На практике часто, но не всегда, принято раскладывать 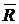 на два ортогональных направления: горизонтальное
на два ортогональных направления: горизонтальное  и вертикальное
и вертикальное 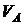 , которые обозначаются двумя опорными стержнями – носителями этих двух составляющих (рис. 3.15, в). Тогда
, которые обозначаются двумя опорными стержнями – носителями этих двух составляющих (рис. 3.15, в). Тогда 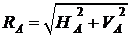 ,
, 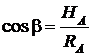 .
.
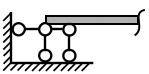
Реакции заделки.Крепление балки АВ, один конец которой заделан в стену, называют заделкой в точке А (рис. 3.16), или консолью.

| 
| 
| |||
| а б в Рис. 3.16 | |||||
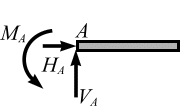
Жесткое закрепление, или заделка, не допускает поворота опорного сечения и его перемещения по горизонтали и вертикали, т. е. на это сечение наложено три связи. В такой опоре возникают три реакции: 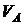 ,
, 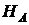 и реактивный момент
и реактивный момент 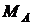 (рис. 3.16, в).
(рис. 3.16, в).
Распределенные нагрузки
Прямоугольно-распределенная нагрузка. Пусть на участке аб, длина которого 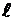 (рис. 3.17, а), равномерно распределена нагрузка интенсивностью
(рис. 3.17, а), равномерно распределена нагрузка интенсивностью 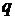 . Распределенную нагрузку заменяем сосредоточенной силой –
. Распределенную нагрузку заменяем сосредоточенной силой – 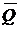 , направленной параллельно силам и приложена в середине отрезка аб:
, направленной параллельно силам и приложена в середине отрезка аб:
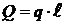 .
.

| 
|
| а | б |
| Рис. 3.17 | |
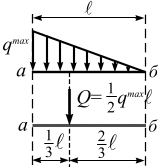
Треугольно-распределенная нагрузка. На участок аб (рис. 3.17, б), длина которого 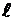 , приложена треугольно-распределенная нагрузка интенсивностью
, приложена треугольно-распределенная нагрузка интенсивностью 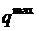 . Равнодействующая
. Равнодействующая 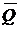 треугольно-распределенной нагрузки направлена параллельно
треугольно-распределенной нагрузки направлена параллельно 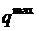 , приложена в точку, которая делит отрезок аб в соотношении
, приложена в точку, которая делит отрезок аб в соотношении 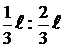 .
. 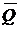 расположена ближе к большей интенсивности и равна
расположена ближе к большей интенсивности и равна
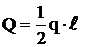 .
.
Дата добавления: 2018-05-12; просмотров: 973; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!