ПРИМЕНЕНИЕ МОДЕЛЕЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ

В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ

 

 

Подходы по формированию уравнений множественной регрессии

 

Множественная регрессия – это уравнение связи с несколькими независимыми переменными, т.е.

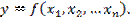                                                    (4.1)

где  y – зависимая переменная (результативный признак);

x₁, x₂, …, x_n - независимые переменные (факторы).

Для построения уравнения множественной регрессии чаще всего используются следующие функции:

 линейная –

                             степенная – 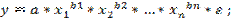                          (4.2)

                             экспонента –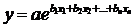

                             гипербола – .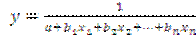

 

 Для оценки параметров уравнения множественной регрессии также используется МНК, сущность которого заключается в составлении системы нормальных уравнений, их преобразований и последующего нахождения параметров регрессии.

На практике часто используют другой подход по определению параметров множественной регрессии, сущность которого заключается в построении на начальном этапе исследования уравнения регрессии в стандартизированной форме и дальнейших его преобразований в ходе последующих этапов.

Уравнение множественной регрессии в стандартизованной форме имеет вид:

 

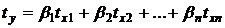,                                (4.3)

где 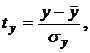 - стандартизованные переменные;

    - стандартизованные коэффициенты регрессии.

Особенностью уравнения вида (4.3) является то, что к нему применимы положения метода наименьших квадратов.

Стандартизованные коэффициенты регрессии определяются из следующей системы уравнений:

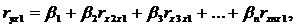
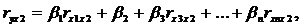                                (4.4)

………………………………………………………….

    

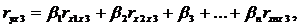
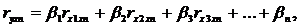
где r_yx1, r_yx2,… r_yxn, r_x1x2, r_x3x2,… r_xnx1 – частные коэффициенты линейной корреляции;

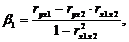
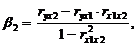
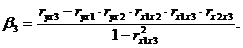  (4.5)

Связь коэффициентов множественной регрессии b_i  со стандартизованными коэффициентами β_i описывается соотношением:

                                                       (4.6)

где σ_xi, σ_y – средние квадратические отклонения соответственно факторов x_i и результативного фактора y.

Из выражения (4.6) получаем формулу перехода от коэффициентов β_i к коэффициентам b_i, необходимую для построения уравнений регрессии в естественной форме

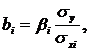                                                       (4.7)

Параметр a применительно к уравнению множественной линейной регрессии (4.2) определяется по формуле (4.8):

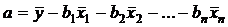.                         (4.8)

Таким образом, на основе проведенных вычислений определяются все составляющие уравнения множественной регрессии в естественной форме (4.2)

.                               

 

Оценка тесноты взаимосвязи факторов множественной регрессии

 

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (R_yx1x2…xn), для определения которого используется выражение 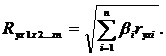(4.9):

                                      (4.9)

Кроме того, используя рекуррентные выражения (4.10)-(4.12), могут дополнительно рассчитываться частные коэффициенты множественной корреляции, которые оценивают влияние фактора x_i  на  y  при неизменном уровне других:

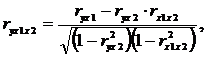                                                    (4.10)                           

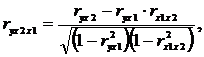                                           (4.11)

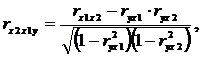                                            (4.12)

где r_yx1x2, r_yx2x1, r_x2x1y– частные коэффициенты множественной корреляции (показывают степень влияния одного фактора x на результативный фактор y при фиксированном значении другого фактора x, а также степень влияния одного фактора x на другой фактор x при фиксированном значении результативного фактора y). Значения частные коэффициентов множественной корреляции изменяются в пределах от -1 до + 1.

Для характеристики относительной силы влияния факторов x_i на y могут рассчитываться средние (частные) коэффициенты эластичности (4.13), показывающие, на сколько % в среднем изменится анализируемый показатель (у) с изменением на 1% каждого фактора при фиксированном значении других факторов:

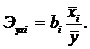                                                       (4.13)

С целью оценки адекватности модели также используют общий критерий Фишера (F-критерий), проверяющий основную гипотезу (H₀) о статической значимости уравнения множественной регрессии и показателя тесноты связи (R_yx1x2…xn). Для этого используется формула (4.14):

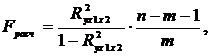                                       (4.14)

где m - число независимых факторов регрессии (для примера 4.1 m = 2 (x₁, x₂);

По таблицам F – критерия (приложение А) находится значение F_табл

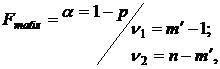                                          (4.15)

 где 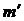- число коэффициентов (параметров) уравнения регрессии ( 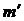=3 (a, b_1, b₂).

Основная гипотеза(H₀) принимается, если F_табл < F_расч; в этом случае с вероятностью  p = 1 – 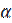 = 0,95 делается заключение о статистической значимости уравнения в целом и показателя тесноты связи R_yx1x2…xn, которые сформировались под воздействием факторов x₁, x₂,… x_n.  

Частные F-критерии - F_x1 и  F_x2 оценивают статическую значимость присутствия факторов x₁ и x₂ в уравнении множественной регрессии. Кроме того, F_x1 оценивает целесообразность включения в уравнение фактора x₁ после того, как в него был включен фактор x₂. Соответственно F_x2 указывает на целесообразность включения в модель фактора x₂ после фактора x₁.

Расчетные значения частных критериев определяются по формулам (4.16) и (4.17):

                              (4.16)

                              (4.17)

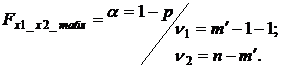                    (4.18)

В данном случае основная гипотеза(H₀) принимается(является статистически значимой) такжепри условии, что F_табл < F_расч.

Примечание: при обосновании объема исследуемой выборки (n) считается оптимальным наличие 6-7 точек наблюдения на каждый фактор уравнения множественной регрессии.

Ниже приведены примеры применения многомерного корреляционно – регрессионного анализа.

 

---

Дата добавления: 2018-05-12; просмотров: 341; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!