Пример 6.8.3-1. Найти минимум функции Q(x,y) методом ГДШ.

Пусть Q(x,y) = x² +2y²; x₀ = 2;y₀ = 1.

Проверим достаточные условия существования минимума:

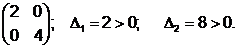
Проделаем одну итерацию согласно алгоритму.

1.Q(x₀,y₀) = 6.

2.При х = x₀ и y = y₀ ,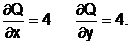

3.Шаг l_k = l₀ = 0,5

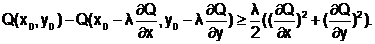
Таким образом, 4 < 8, следовательно, условие сходимости не выполняется и требуется, уменьшив шаг (l=l /2), повторять п.п.3-4 до выполнения условия сходимости. То есть, полученный шаг используется для нахождения следующей точки траектории спуска.

Метод наискорейшего спуска

Суть метода состоит в следующем. Из выбранной точки (x₀,y₀) спуск осуществляют в направлении антиградиента до тех пор, пока не будет достигнуто минимальное значение целевой функции Q(x, y) вдоль луча (рис. 6.8.4-1). В найденной точке луч касается линии уровня. Затем из этой точки спуск проводится в направлении антиградиента (перпендикулярном линии уровня) до тех пор, пока соответствующий луч не коснется в новой точке проходящей через нее линии уровня, и т.д.

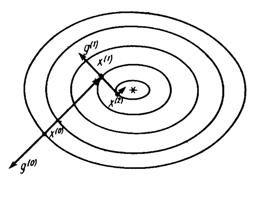
Рис. 6.8.4-1

Выразим целевую функцию Q(x, y) через шаг l. При этом представим целевую функцию на определенном шаге как функцию одной переменной, т.е. величины шага

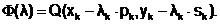
Величина шага на каждой итерации определяется из условия минимума :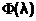

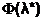= min( 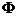(l)) l_k = l*(x _k, y _k), l >0.

Таким образом, на каждой итерации выбор шага l_k предполагает решение задачи одномерной оптимизации. По способу решения этой задачи различают:

· аналитический метод (НСА);

· численный метод (НСЧ).

В методе НСА значение шага получают из условия 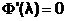, а в методе НСЧ величину l_k находят на отрезке [0;1] c заданной точностью, используя один из методов одномерной оптимизации.

Пример 6.8.4-1. Найти минимум функции Q(x,y)=x² + 2y²с точностью e=0.1, при начальных условиях: x₀=2; y₀=1.

Проделаем одну итерацию методом НСА.

Выразим целевую функцию через величину l:

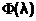=(x-2lx)²+2(y-4ly)² = x²-4lx²+4l²x²+2y²-16ly²+32l²y².

Из условия 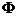¢(l)=0 найдем значение l*: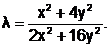

Полученная функция l=l(x,y) позволяет найти значение l. При x=2 и y=1 имеем l=0.3333.

Вычислим значения координат следующей точки:

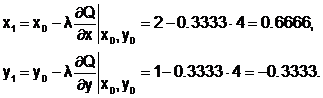
Проверим выполнение критерия окончания итераций при k=1:

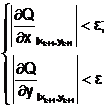
Поскольку |2*0.6666|>0.1 и |-0.3333*4|>0.1 , то условия окончания процесса итераций не выполнены, т.е. минимум не найден. Поэтому следует вычислить новое значение l при x=x₁ и y=y₁ и получить координаты следующей точки спуска. Вычисления продолжаются до тех пор, пока не выполнятся условия окончания спуска.

Отличие численного метода НС от аналитического состоит в том, что поиск значения l на каждой итерации происходит одним из численных методов одномерной оптимизации (например, методом дихотомии или методом золотого сечения). При этом в качестве интервала неопределенности служит диапазон допустимых значений l - [0;1].

Проблема оврагов. Метод покоординатного спуска

К сожалению, выбор антиградиента в качестве направления спуска не всегда является удачным. Особенно ярко это проявляется для овражных функций.

Градиентный метод сходится достаточно быстро, если для минимизируемой функции поверхности уровня близки к сферам (при m=2 линии уровня близки к окружностям).

Действительно, известно, что градиентный метод сходится очень медленно, если поверхности уровня минимизируемой функции сильно вытянуты в некоторых направлениях.

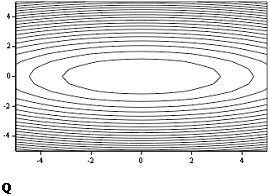
В двумерном случае рельеф соответствует поверхности U=Q(x₁,x₂) и напоминает рельеф местности с оврагом. Поэтому эти функции называют «овражными» (рис.6.8.5-1).

Вдоль направлений, характеризующих «дно оврага», «овражная» функция меняется незначительно, а в других направлениях, характеризующих «склон оврага», происходит резкое изменение значений функции.

Если начальная точка Х₀ попадает на «склон оврага» , то направление градиентного спуска оказывается почти перпендикулярным «дну оврага» и очередное приближение Х₁ попадает на противоположный «склон оврага».

Следующий шаг в направлении ко «дну оврага» возвращает приближение Х₂на противоположный «склон оврага» и т.д.

В результате вместо того, чтобы двигаться вдоль оврага (в направлении точки минимума), траектория спуска совершает зигзагообразные скачки поперек «оврага».

Рис. 6.8.5-1

Один из существенных недостатков градиентного метода связан с его чувствительностью к погрешностям вычислений. Особенно сильно этот недостаток сказывается в малой окрестности точки минимума, где антиградиент, задающий направление поиска, мал по модулю. Поэтому эффективность градиентного метода на завершающей стадии существенно ниже, чем на начальной стадии.

Проблему «оврагов» позволяют решать специально разработанные «овражные» и другие методы спуска, например, метод покоординатного спуска.

В методе покоординатного спуска в качестве очередного направления спуска выбирают направление одной из координатных осей. Наиболее известным является метод циклического покоординатного спуска.

Рассмотрим очередной n+1 цикл одного из вариантов этого метода, считая, что приближение к минимуму функции Q(X)=Q(x₁, … x_m) уже найдено Х_n.

1-й шаг. На первом шаге проводят спуск по координате x₁. Значения остальных координат x₂= x₂⁽ⁿ⁾, x₃= x₃⁽ⁿ⁾ , … , x_m = x_m⁽ⁿ⁾ фиксируют, а x₁⁽ⁿ⁾выбирают из условия:

Q(x₁⁽ⁿ⁺¹⁾ , x₂⁽ⁿ⁾ … x_m⁽ⁿ⁾) = min Q(x₁, x₂⁽ⁿ⁾ … x_m⁽ⁿ⁾)

x₁

Фактически решается задача минимизации функции одной переменной.

Q(x1) = min Q(x1, x2(n) … xm(n) ).

2-шаг. На втором шаге производится спуск по координате x₂. Значения остальных координат x₁= x₁⁽ⁿ⁾, x₃= x₃⁽ⁿ⁾ , … , x_m = x_m⁽ⁿ⁾ фиксируют, а x₂⁽ⁿ⁺¹⁾выбирают как решение задачи одномерной оптимизации

Q(x₁⁽ⁿ⁺¹⁾ , x₂⁽ⁿ⁺¹⁾, x₃⁽ⁿ⁾ … x_m⁽ⁿ⁺¹⁾) = min Q(x₁⁽ⁿ⁺¹⁾, x₂, x₃⁽ⁿ⁾ … x_m⁽ⁿ⁾).

x₂

Аналогично осуществляют следующие шаги.

m-й шаг. На последнем шаге координату x_m⁽ⁿ⁺¹⁾ определяют из условия

Q(x₁⁽ⁿ⁺¹⁾ , x₂⁽ⁿ⁺¹⁾, … x_m_-1⁽ⁿ⁺¹⁾,x_m⁽ⁿ⁺¹⁾) = min Q(x₁⁽ⁿ⁺¹⁾, … x_m_-1⁽ⁿ⁺¹⁾,x_m).

x₂

В результате получается очередное приближение x⁽ⁿ⁺¹⁾ к точке минимума.

Далее цикл метода снова повторяется. Каждый цикл метода состоит из m шагов (т.е. по количеству переменных). Т.к. на k-том шаге очередного цикла значение координаты x_k⁽ⁿ⁺¹⁾ определяют из условия минимизации функции f по направлению x_k, то необходимо, чтобы в точке (x₁⁽ⁿ⁺¹⁾ , x₂⁽ⁿ⁺¹⁾, … x_k_-1⁽ⁿ⁺¹⁾, x_k, x_k₊₁⁽ⁿ⁺¹⁾, …x_m⁽ⁿ⁺¹⁾) производная 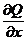обращалась в ноль.

На рисунке изображена графическая иллюстрация циклического покординатного спуска для случая m=2.

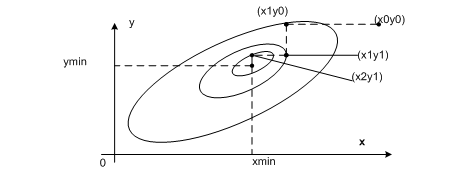
Рис. 6.8.5-2

Дата добавления: 2018-05-12; просмотров: 310; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 11 12 13 141516 Следующая ⇒

Мы поможем в написании ваших работ!