Определение рабочих отметок вершин
Осуществляем по формуле:
hрi= Hki- Hi , м (1.5)
h 1 = 36,22-35,44= +0,78 м,
h 2 = 36,16-35,27= +0,89м,
h 3 = 36,09-35,26= +0,83м,
h 4 = 36,03-34,71= +1,32м,
h 5 = 36,42-36,66=-0,24 м,
h 6 = 36,35-36,50=-0,15 м,
h 7 = 36,29-35,95=+0,34 м,
h 8 = 36,22-35,17=+1,05 м,
h 9 = 36,61-37,93=-1,32 м,
h 10 = 36,55-37,46=-0,91 м,
h 11 = 36,48-36,44=+0,04 м,
h 12 = 36,42-35,61=+0,81 м,
Если h i меньше 0, то мы имеем дело с выемкой, если же hi> 0 - с насыпью. Красные, черные и рабочие отметки приведены в таблице 2 расчета по программе "TSP" и на рисунке 5 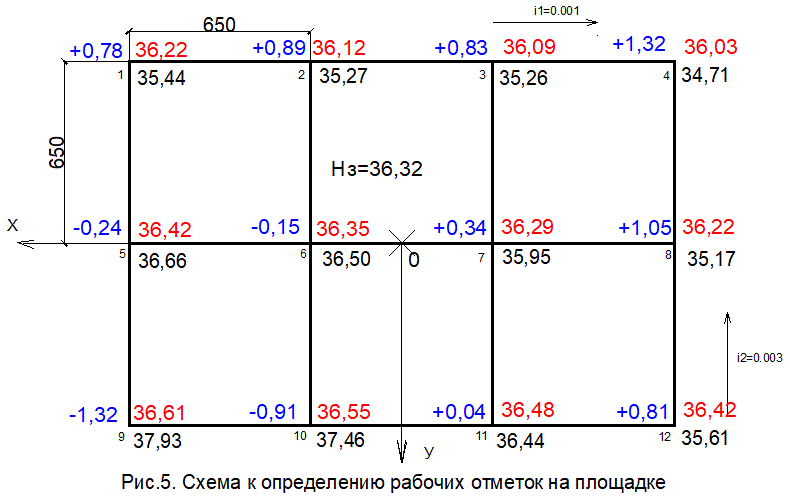 .
.
Построение линии нулевых работ (л.н.р.)
Л.н.р. представляет собой линию пересечения проектной плоскости с поверхностью земли. Л.н.р. пресекает ту сторону квадрата или треугольника, на концах которой рабочие отметки имеют разный знак. Положение л.н.р. на стороне квадрата аналитическим осуществляется по формуле (рис.6):
| 1 |
| 5 |
| h5 |
| h1 |
| L1-5 |
| а = 65 |
Рис.6. Схема к определению положения л.н.р. аналитическим или графическим способом
L i-j= (h i·а)/(|h i|+|h j|) , м (1.6)
где: L i-j - расстояние от вершины с номером i до точки, принадлежащей Л.Н.Р. (рис. 6), м;
h i - рабочая отметка вершины с номером i, м;
h j - рабочая отметка вершины j на другом конце пересекаемой л.н.р. стороны, м;
а - длина стороны квадрата, м.
Например, для стороны 1– 5
 L1-5= |0,78|·65/(|-0,24|+|0,78|) = 49.70 м,
L1-5= |0,78|·65/(|-0,24|+|0,78|) = 49.70 м,
L6-7= |-0,15|·65/(|-0,15|+|0,34|) = 19.90 м,
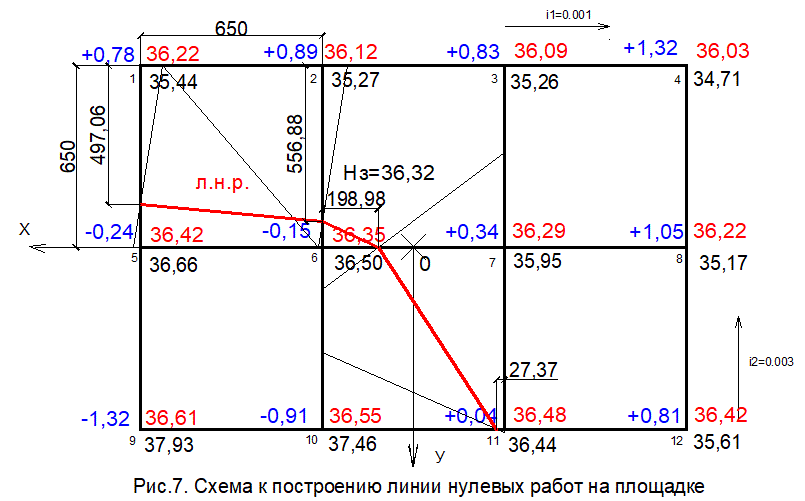
Удобно использовать для определения точек нулевых работ средуAutoCad, то есть использовать графический способ определения точек.При построении л.н.р. полученные на сторонах точки соединяем между собой прямыми.Схема определения линии нулевых работ приведена на рисунке 7.
Определение частных объемов
Определение частных объемов целых квадратов и треугольников (не пересекаемых л.н.р.)
а) при определении объемов способом квадратных приз:
h1 h2
V3= a2(h1 + h2 + h3+h4)/4 ,м3 (1.7)
a где: h1, h2, h3,h4 - рабочие отметки в вершинах квадрата, м. a – сторона квадрата, м.
Для квадрата №3 на рисунке 8
V3кв=652*(0,83+1,32+1,05+0,34)/4=3739,13м3
h3h4
Рис. 8. Схема целого квадрата
б) при определении объемов способом треугольных призм (рис. 9):
| a |
| h1 |
| h2 |
| h3 |
| |
Vn = a2(h1 + h2 + h3)/6 , м3 (1.8)
где: h1, h2, h3 - рабочие отметки в вершинах треугольника, м.
Рис.9. Схема целого треугольника
Определение объемов переходных квадратов и треугольников, пересекаемых л.н.р.
а) при определении объемов способом квадратных призм.
При переходном квадрате 1-го типа (рисунок 10) вначале по формуле 1.7 находим балансовый объем V n. Затем находим объем треугольной части квадрата по формуле:
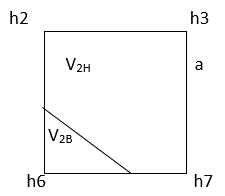
V2В= (a2*h63)/((|h6|+|h2|)*(|h6|+|h7)*6) , м3(1.9)
где: h6 - рабочая отметка, принадлежащая треугольной части квадрата, м;
h2, h7 – рабочие отметки вершин, располагаемых по сторонам квадрата напротив вершин с отметкой h6, м
a – сторона квадрата, м.
Рис. 10. Схема переходного квадрата 1-го типа
На заключительном этапе находим объем пятиугольной части квадрата V2Н:
V2Н=V2кв-V2В (1.10)
V2кв=652*(0,89+0,83-0,15+0,34)/4=2017.44м3
V2В= 652*(-0,15)3/((0,89+0,15)*(0,15+0,34)*6)=-4,66м3
V2Н=2017,44-(-4,66)=2022,10 м3
При переходном квадрате 2-го типа (рисунок 11) объемы насыпи и выемки определяются по выражения:
+h1 a +h2
Vi= (a2/4)*((h12/(|h1|+|h5|)*(h22 /(|h2|+|h6|))м3 (1.11)
V1Н
где: h1, h2, h5,h6 - рабочие отметки в вершинах треугольника, м., a – сторона квадрата, м.
V1В
-h5-h6
Рис.11. Схема переходного квадрата 2-го типа
Для квадрата №1 объемы выемки и насыпи равны:
V1Н= (652/4)*((0,78)2/(0,78+0,24)+((0,89)2/(0,89+0,15))=1434,50м3
V1В= (652/4)*((-0,24)2/(0,78+0,24)+((-0,15)2/(0,15+0,89))=-82,50м3
Объемы остальных фигур приведены в таблице 4 расчета по программе "TSP"
б) при определении объемов способом треугольных призм.
Вначале по формуле 1.7 находим балансовый объем V n. Затем находим объем треугольной части треугольника по формуле:
Vn3 = a2·h13 / [(|h1| + |h2|)* (|h1| + |h3|)·6 ] , м3 (1.12)
| Рис.12. Схема переходноготреугольника |
| h1 |
| h2 |
| h3 |
| Vn4 |
| Vn3 |
| "n" |
| л.н.р. |
Объем четырехугольной части треугольника будет равен:
Vn4 = Vn - Vn3 (1.13)
Дата добавления: 2018-05-12; просмотров: 2498; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
