Основные теоремы электродинамики

Лекция № 3. Дифференциальные операции в скалярных и векторных полях

Учебные вопросы лекции:

Дивергенция.

Ротор.

Основные теоремы электродинамики.

Введение

Из предыдущей лекции установлено, что векторные и скалярные поля определяются различными способами, при этом их графическое изображение раскрывает их математическую сущность. Очевидно, что между этими полями существует взаимосвязь, поскольку они отражают разные представления одного и того же электромагнитного поля.

В качестве связующих инструментов между скалярными и векторными полями выступают дифференциальные векторные операторы, отображающие одни поля на другие.

В данной лекции подробно раскрываются дифференциальные характеристики, наглядно описывающие поля в бесконечно малых физически участках пространства, которые упрощенно будем называть точками поля.

Дивергенция векторного поля

Анализ векторных полей в отличие от скалярных полей является более трудной задачей, поскольку векторные поля имеют более сложную структуру. Это связано с характером поведения векторных линий в различных точках пространства. В векторном поле могут существовать точки пространства, в которых векторные линии могут начинаться или заканчиваться. Если какая либо точка пространства является началом векторных линий, то говорят, что в этой точке пространства находится источник векторного поля. Точка же пространства, в которой заканчиваются векторные линии, называется стоком. Например, для электрического поля источниками и стоками являются, соответственно, положительные и отрицательные заряды. Чем больше векторных линий начинается в данной точке пространства, тем мощнее, обильнее находящийся в этой точке пространства источник.

Из приведенных рассуждений следует, что в некоторых точках векторного поля может наблюдаться расходимость силовых линий от источника, а в других – наоборот сходимость линий к стоку. В связи с этим, для количественной оценки векторного поля в различных точках пространства в теории поля введена скалярная функция, называемая дивергенция (от латинского слова divergentia – расхождение, расходимость). Заметим, что вся терминология пришла из гидродинамики, поэтому для наглядности можно представлять себе поле скоростей при течении жидкости, например, в ванне. Тогда источник – это водопроводный душ, от которого расходятся струи воды, а сток – устройство слива, куда сходятся все струи воды.

Итак, в данном вопросе рассмотрим еще одну, имеющую большую значимость в теории поля, дифференциальную операцию 1-го порядка – дивергенцию. В противоположность операции градиента, превращающего скалярное поле в векторное поле, дивергенция действует на векторные поля, а результатом преобразования получается скалярное поле.

Введем математическое описание дивергенции. Для этого сформулируем задачу: необходимо получить дифференциальный оператор, осуществляющий преобразование (отображение) векторного поля сил, определенного в некотором пространстве V, в поле скалярных величин, характеризующих наличие или отсутствие в точках пространства V источников или стоков поля.

В предыдущей лекции была получена интегральная характеристика векторного поля – поток Ф, определяющая величину (силу) поля в замкнутом объеме V ограниченном замкнутой поверхностью S. Получение поля скалярных величин, определяющих для каждой точки поля расходимость или сходимость входящих и исходящих линий, возможно за счет операции дифференцирования этой интегральной характеристикиФпо объемуV для каждой точки пространства.

Таким образом, математически дивергенция – это дифференциальный оператор 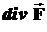, отображающий векторное поле на скалярное, то есть осуществляющий операцию дифференцирования, в результате применения которой к векторному полю получается скалярное поле.

Дивергенция векторного поля определяется производной по объему:

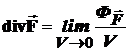, , (1)

где 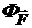– поток векторного поля через любую поверхность площадью S, ограничивающую объём V, при условии, что поверхность находится внутри сферы радиусом, стремящимся к нулю.

Если векторное поле дифференцируемо в некоторой области, тогда в трёхмерном декартовом пространстве дивергенция будет определяться скалярным произведением оператора набла и вектора поля :

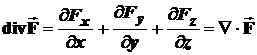, (2)

где – векторный дифференциальный оператор набла.

Физический смыслдивергенции векторного поля состоит в том, что эта характеристика показывает то, в какой степени данная точка пространства (точнее достаточно малая окрестность точки) является источником или стоком этого поля:

- если 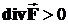, тогда точка поля является источником или истоком (см. рис. 1, а);

- если 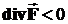, тогда точка поля является стоком (см. рис. 1, б);

- если 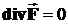, тогда стоков и источников нет, либо они компенсируют друг друга (см. рис. 1, в);.

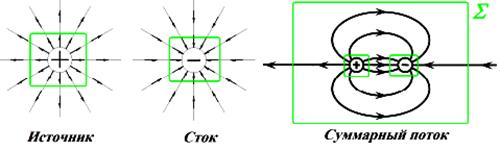
а) б) в)

Рис. 1 – Дивергенция

Простейшей моделью, поясняющей суть дивергенции, может служить озеро постоянной единичной глубины со всюду постоянной горизонтальной скоростью течения воды, не зависящей от глубины. В этой модели родники, бьющие из дна озера, будут давать положительную дивергенцию поля скоростей течения, а подводные пещеры, то есть стоки, куда вода утекает – отрицательную дивергенцию.

Дивергенция вектора плотности тока даёт минус скорость накопления заряда в электродинамики, так как заряд сохраняется, то есть не исчезает и не появляется, а может только переместиться через границы какого-то объёма, чтобы накопиться в нём или уйти из него; а если и возникают или исчезают где-то положительные и отрицательные заряды, то только в равных количествах.

Геометрическая интерпретация. Если в качестве векторного поля (на двумерном пространстве) взять совокупность направлений наискорейшего спуска на земной поверхности, то дивергенция покажет местоположение вершин и впадин, причём на вершинах дивергенция будет положительна (направления спуска расходятся от вершин), а на впадинах отрицательная (ко впадинам направления спуска сходятся).

Свойства дивергенции вытекают из обычных правил дифференцирования, к ним относятся:

1) Линейность: для любых векторных полей F и G и для всех вещественных чисел a и b имеет место равенство

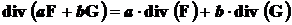. (3)

Если φ — скалярное поле, а F — векторное, тогда:

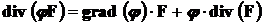. (4)

2) Свойство, связывающее векторные поля F и G, заданные в трёхмерном пространстве, с ротором:

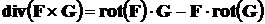. (5)

3) Дивергенция от градиента есть лапласиан:

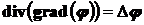. (6)

4) Дивергенция от ротора:

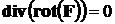. (7)

Таким образом, в данном вопросе установлено, что векторные поля силы преобразуются в скалярные поля дифференциальным оператором дивергенция, который математически представляет собой скалярное произведение векторного оператора набла на вектор силы. Дивергенция определяет, в какой степени точка пространства является источником или стоком этого поля.

Ротор

В предыдущей лекции установлено, что циркуляция С характеризует вращательную способность векторного поля вдоль некоторой замкнутой кривой L в некотором объеме V. Очевидно, что характеризовать завихрённость поля непосредственно циркуляцией нельзя, поскольку поле может быть очень неоднородным, и степень его завихрённости будет изменяться от точки к точке. Таким образом, стоит задача определить «локальную» завихрённость поля в каждой точке пространства, или по-другому переопределить векторное поле сил в векторное поле вихрей.

Для решения этой задачи необходимо уменьшать размеры контура L, стягивая его в точку, т.е. L ® 0, тогда циркуляция С тоже будет стремиться к 0. Поэтому для характеристики степени завихрённости поля вводят понятие плотности циркуляции, определяя её как предел, к которому стремится отношение циркуляции вектора 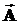по контуру L, к площади DS, ограниченной этим контуром, когда данный контур стягивается к рассматриваемой точке пространства M (в этом случае DS ®0). В результате получен векторный дифференциальный оператор над векторным полем, имеющий смысл плотности циркуляции. Полученный вектор пока условно назовем ротором:

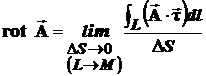. (8)

Вычисляя этот предел, получим уже некоторое конечное, отличное от нуля число. Это значение будет зависеть от ориентации контура L в поле. Например, как уже говорилось ранее, от ориентации турбины в жидкости. Изменяя ориентацию турбины, можно получить максимальное и минимальное значения циркуляцииС (соответствующие двум противоположным ориентациям турбинки, при этом одно из них будет положительным, а другое отрицательным), а также при некоторой ориентации турбина вообще перестанет вращаться, что соответствует С=0. Данные обстоятельства показывают, что всё многообразие значений плотности циркуляции векторного поля может быть, вообще говоря, представлено в виде проекции некоторого вектора 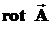на вектор нормали 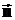к площадке контура L (см. рис. 2).

Рис. 2 – Вихревое поле и его ротор

Данный вектор называется ротором или вихрем векторного поля 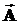(от французского (или английского) слова rotation – вращение, или лат. roto – вращаюсь). Он по абсолютной величине будет численно равен максимальному значению плотности циркуляции вектора 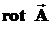в рассматриваемой точке пространства М, и направлен в сторону, соответствующую направлению нормали к контуру L, при которой плотность циркуляции принимает это максимальное значение.

Математически ротор представляет собой вектор, проекция которого 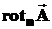на каждое направление вектора нормали 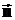есть предел отношения циркуляции векторного поля по контуру L, являющемуся краем плоской площадки ΔS, перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:

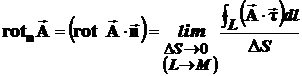, (9)

где еще раз уточним 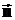– нормаль к площадке DS, согласованная с направлением обхода контура Lправилом правого винта (буравчика) как на рис. 5.

В трёхмерной декартовой системе координат ротор векторного поля вычисляется следующим образом:

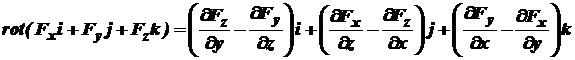, (10)

где i, j и k – единичные орты (векторы) для осей x, y и z соответственно.

Для удобства запоминания можно условно представлять ротор в матричном виде как векторное произведение, формально представляющее векторное произведение как определитель:

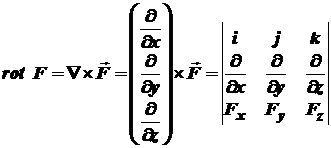. (11)

Физический смысл ротора в гидродинамики заключается в том, что дает представление о вращении брошенной в поток маленькой пылинки (увлекаемой потоком с собой, без его заметного возмущения) или о вращении помещённого в поток с закреплённой осью маленького колеса (турбины) с прямыми (не винтовыми) лопастями. Если то или другое при взгляде на него вращается по часовой стрелки, то это означает, что вектор ротора поля скорости потока в данной точке имеет проекцию в направлении от наблюдателя. Следует иметь в виду, что завихренность поля (вращательная компонента) может быть обусловлена не только искривлением векторных линий (завихрённость «в чистом виде»), как при вытекании воды из ванны, или в примере е), но и поперечной неоднородностью поля, когда векторные линии прямые, как в случае течения воды в реке (см. рис. 6). В этом случае, как показано на рис. 3, турбина будет вращаться по часовой стрелке по причине неоднородности поля скоростей движения воды в реке, т.к ее течение более быстро в верхних слоях, чем в нижних.

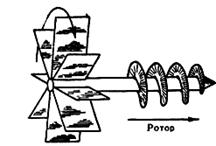
Рис. 3 – Пример образования и физический смысл ротора

Основные свойства ротора:

1) Дивергенция ротора векторного поля равна нулю:

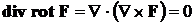, (12)

то есть поле не имеет источников. При этом верно и обратное: если поле F бездивергентно, оно есть поле ротора некоторого потенциального поля G (векторного потенциала):

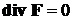
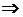
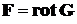. (13)

2) Если поле F потенциально, то его ротор равен нулю в любой точке поля, то есть поле F является безвихревым:

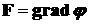
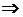
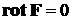. (14)

Верно и обратное: если поле безвихревое, то оно потенциально для некоторого скалярного поля j.

3) Ротор от ротора равен градиенту дивергенции минус лапласиан:

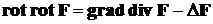. (15)

Кроме того ротор, как и все дифференциальные операторы имеют свойство линейности, т.е. для любых векторных полей Fи Gи для любых постоянных чисел aи b выполняется равенство:

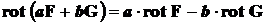. (16)

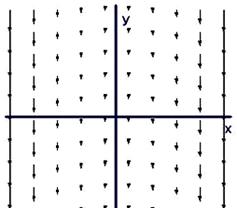
Рассмотрим векторное поле F, зависящее от координат xи yтак: 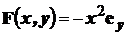. Его график приведен на рис. 4, а).

Анализ графика на рис. 4 а) показывает, что не наблюдается никакого вращения, но, посмотрев по внимательнее видно, что по краям оси х сила поля больше, чем в середине. Если установить маленькое колесо с лопастями в правой стороне, то больший поток на этой стороне заставил бы колесо вращаться по часовой стрелке, что соответствует ввинчиванию в направлении -z. Если расположить колесо в левой части поля, то больший поток на его левой стороне заставил бы колесо вращаться против часовой стрелки, что соответствует ввинчиванию в направлении +z.

а) б)

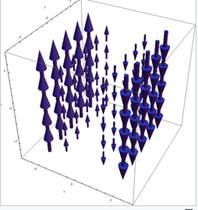
Рис. 4 – Векторное поле и его ротор

Проверим полученные выводы с помощью вычисления:

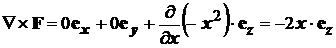Действительно, ввинчивание происходит в направлении +z для отрицательных x, и –z для положительных x, как и ожидалось. При этом ротор не одинаков в каждой точке, как видно на рис. 4, б).

В заключение этого вопроса рассмотрим ряд примеров векторных полей, приведенных на рис. 5, и для закрепления учебного материала определим, где их дивергенцию и роторы равны нулю, а где нет. При решении данных задач, прежде всего, нужно обратить внимание на контуры интегрирования, заметив, что они выбраны так, чтобы вдоль каждой из сторон, проекция векторов поля имела одно и тоже значение (причём для двух сторон в случаях а, б, г, д она равна 0).

Рис. 5 Примеры векторных полей

Ответы:

a) , 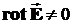вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. ротор не равен нулю. Сравните с рекой.	б) 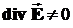, 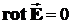Явно виден источник поля. Дивергенция не равна нулю. Поле центрально - симметричное. Поэтому ротор равен 0.	в) , 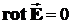вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Проекции векторов поля на противоположные стороны контура разных знаков, но одинаковы по абсолютной величине, и поэтому при сложении линейных интегралов они уничтожают друг друга. Поэтому ротор равен нулю.
г) , 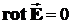вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор убывает по мере удаления от центра поля (за пределами рисунка) поэтому ротор может быть равен 0.	д) , 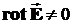вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор не убывает, поэтому линейный интеграл по левой стороне контура не компенсируется таким же интегралом по правой. Поэтому ротор не равен нулю.	е) 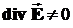, 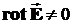Явно виден сток поля. Поэтому дивергенция не равна 0. Так же и ротор не равен нулю, поскольку циркуляция вдоль указанного контура не равна 0, так как проекции векторов поля на все стороны контура одного знака (отрицательны) и при сложении (интегрировании) не компенсируют друг друга.

Подводя итог, ещё раз отметим, что ротор характеризует степень завихрённости векторного поля, его «вращательную составляющую» в каждой точке пространства.

Через понятие ротор принято выражать одно из уравнений Максвелла, описывающее закон электромагнитной индукции Фарадея. Данный закон говорит, что ротор электрического поля равен скорости изменения магнитного поля, взятой с обратным знаком, а ротор напряжённости магнитного поля равен сумме плотностей тока обычного и тока смещения.

Основные теоремы электродинамики

Дата добавления: 2018-05-12; просмотров: 1270; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!