Интегральные характеристики векторных полей
Лекция № 2. Элементы векторного анализа
Учебные вопросы лекции:
Умножение векторов.
Интегральные характеристики векторных полей.
Градиент. Операторы Гамильтона (набла) и Лапласа.
Введение
Максвелл, создавая математическую формулировку уравнений электромагнитного поля, строил свою теорию на понятиях и элементах векторного анализа, использовав компактную кватернионную запись своих уравнений.
В дальнейшем английский ученый Оливер Хэвисайд переформулировал уравнения Максвелла в терминах трехмерных векторов напряжённостей электрического и магнитного полей, электрической и магнитной индукций, придав им современный вид в элементах векторного анализа.
Применение векторного анализа в теории ЭМП связано с рядом преимущества векторных методов описания перед традиционными координатными методами:
1) Компактность. Одно векторное уравнение объединяет несколько координатных, и его исследование чаще всего можно проводить непосредственно, не заменяя векторы на их координатную запись.
2) Инвариантность. Векторное уравнение не зависит от системы координат и без труда переводится в координатную запись в любой удобной системе координат.
3) Наглядность. Дифференциальные операторы векторного анализа и связывающие их соотношения обычно имеют простое и наглядное физическое толкование.
Поскольку основным математическим аппаратом при расчете ЭМП является векторный анализ, включающий в себя понятия: скаляр, вектор и тензор, то для успешного освоения этого аппарата необходимо глубокое понимание основ векторного анализа, кратко излагаемого в данном учебном вопросе.
|
|
|
Умножение векторов
Из курса векторной алгебры известно, что существует три вида произведения векторов:
- скалярное произведение, результатом которого является скалярная величина,
- векторное произведение, результатом которого является новый вектор,
- смешанное произведение векторов, результатом которого является скалярная величина.
Все эти результаты векторного умножения имеют различный физический смысл, поэтому в теории ЭМП применение этих операций на практике является целесообразным для определения различных характеристик поля.
С помощью векторов в теории ЭМП отображаются силовые характеристики поля, такие как силы  Кулона, Лоренца, Ампера, электрическая
Кулона, Лоренца, Ампера, электрическая 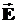 и магнитная
и магнитная 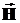 напряженности, электрическая
напряженности, электрическая 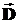 и магнитная
и магнитная 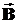 индукции, а также радиус-вектор
индукции, а также радиус-вектор 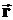 , вектор перемещения
, вектор перемещения 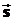 или векторы бесконечно малого радиуса и перемещения drи ds.
или векторы бесконечно малого радиуса и перемещения drи ds.
Рассмотрим типовые ситуации (см. рис. 1) применения различных видов умножения векторов при решении различных физических задачах теории ЭМП.
|
|
|
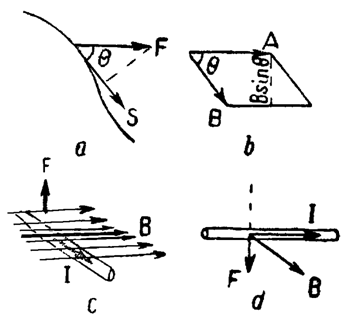
Рис. 3 – Типовые ситуации применения различных видов умножения векторов
Ситуация 1, приведенная на рис. 1 a), демонстрирует случай, когда в результате действия силы поля  на некоторое тело происходит его перемещение на расстояние
на некоторое тело происходит его перемещение на расстояние 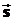 . Из курса механики известно, что произведение силы на расстояние перемещения имеет физический смысл работыA, совершаемой силой поля. Математически это определяется скалярным произведением векторов
. Из курса механики известно, что произведение силы на расстояние перемещения имеет физический смысл работыA, совершаемой силой поля. Математически это определяется скалярным произведением векторов  и
и 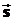 с учетом угла qмежду их направлениями, т.е.
с учетом угла qмежду их направлениями, т.е.
 . (1)
. (1)
В этом случае, как следует из выражения (1), работа, совершённая силой поля, определяется скалярным произведением вектора силы на вектор перемещения, что геометрически соответствует умножению модуля вектора перемещения s на проекцию Fs вектора силы  на вектор
на вектор 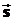 .
.
Случаи, когда для решения физической задачи используется векторное произведение векторов, продемонстрированы на рис. 1 b), 1 c), 1 d). Так на рис. 1 b) показано то, что векторное произведение имеет геометрический смысл, заключающийся в том, что модуль полученного вектора 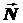 равен площади параллелограмма, образованного исходными векторами
равен площади параллелограмма, образованного исходными векторами  и
и 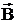 , т.е.
, т.е.
|
|
|

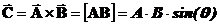 . (2)
. (2)
Векторное умножение,например, используется при определении силы Ампера, действующей на находящийся в магнитном поле проводник с током. Если магнитное поле (см. рис. 1 с) по величине и направлению определяется вектором В, а ток (который предполагается постоянным), вектором I, то сила, действующая на проводник длинной 1 м, будет характеризоваться вектором F, который перпендикулярен как к вектору В, так и к вектору I. Величина вектора F находится из выражения

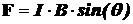 . (3)
. (3)
В выражении (3) результат умножения представляет собой вектор. Однако с первого взгляда неясно, почему площадь на рис. 1 b) представляет собой векторную величину. Понятно только, что поверхность должна быть ориентирована в пространстве. Поэтому условились представлять площадь вектором, направление которого нормально к поверхности, а длина пропорциональна величине площади. Таким образом, площадь на рис. 1 с) изображается вектором, перпендикулярным к плоскости чертежа.
Естественно возникает вопрос о знаке результирующего вектора, что в уравнении (3) показывает, куда направлена сила – вверх или вниз? С тем, чтобы устранить двузначность в математической постановке задачи, условились, что в векторном произведении знак результирующего вектора определяется порядком, в котором записаны векторы, входящие в произведение. Этот способ является достаточно удобным и определённым для установления направления векторного произведения. Однако, выразить словами соответствующие соотношения несколько затруднительно. Обычно правило знака запоминают, располагая определённым образом пальцы правой руки, или пользуясь вращением, так называемого правовинтового винта.
|
|
|
Итак, произведение двух векторов [АВ] само представляет собой вектор величины АВ sin(q), имеющий направление, нормальное к плоскости, в которой лежит как вектор А, так и вектор В, при чём знак направления таков, что если поворачивать правый винт (буравчик), как показано на рис. 2 от А к В (на угол меньший 180°), то он будет ввинчиваться по направлению, определяемому направлением вектора произведения.
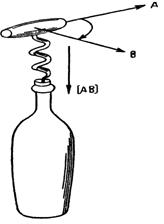
Рис. 2 – Правило правового буравчика (винта)
В соответствии с этим правилом уравнение (3) даёт направление силы. Причём вектор [АВ], характеризующий площадь, изображённую на рис. 1 b), направлен вниз относительно плоскости параллелограмма, тогда как произведение [ВА] соответствует вектору, направленному вверх относительно плоскости параллелограмма. Сказанное представляет собой только иллюстрацию общего правила, согласно которому [ВА] = –[АВ]. Это означает, что рассматриваемая операция векторного умножения не подчиняется основному закону коммутативности обычной алгебры, который говорит, что ab = bа.
Для того, чтобы в вести выражение, однозначно и строго определяющее векторное произведение воспользуемся единичным вектором n, представляющим собой вектором единичной длины, который нормален к плоскости в которой расположены векторы А и В, и имеет такое направление, что образует правовинтовую систему с этими векторами. Таким образом, векторное произведение определяется выражением
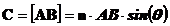 , (4)
, (4)
где А и В представляют собой скалярные величины векторов А и В, q - угол между векторами, т.е. результат векторного произведения представляет собой произведение скаляра, равного площади параллелограмма, на единичный вектор, который служит для указания направления нормали к плоскости векторов А и В, и, следовательно, точно определяет направление векторного произведения.
До сих пор, вектора в лекции рассматривались абстрактно без привязки к координатам пространства. Известно, что положение любой точки в пространстве можно определить, используя декартовы координаты на основании известных методов аналитической геометрии. При этом длина и направление любого вектора выражается с помощью проекций вектора на три оси координат. Тогда любой вектор А может быть описан как имеющий три взаимно перпендикулярных скалярных компоненты (проекции): Ах по направлению х, Ау по направлению у и Аz по направлению z.
Для придания этим скалярным проекциям направленности вводится система из трех ортонормированных векторов или ортов i, j, k, т.е. векторов единичной длины, направленных вдоль оси декартовой системы координат, следовательно, являющихся ортогональными (перпендикулярными) друг к другу.
Свойства единичных векторов представлены системой уравнений (5), содержащей некоторые скалярные и векторные произведения этих векторов:
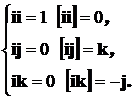 (5)
(5)
Из выражений (5) следует, скалярное произведение одноименных ортов равно единице, а разноименных ортов равно нулю, тогда как векторное произведение одноименных ортов наоборот рано нулю, а разноименных образует третий орт, что подтверждает их ортогональность.
Теперь любой вектор А можно представить в следующем виде:
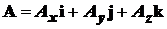 , (6)
, (6)
это означает, что А равен сумме вектора длиной Ах, направленного по х, вектора длиной Аунаправленного по у, и вектора длиной Аг, направленного по z.
Системы координат имеют существенное значение для векторного анализа, и полезно выразить некоторые наиболее важные векторные операции с помощью компонент декартовой системы координат. Так скалярное произведение векторов в декартовой системе координат равно
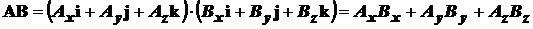 . (7)
. (7)
Векторное произведение каких-либо двух векторов может быть представлено аналогичным образом:
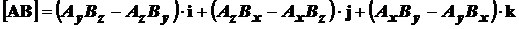 . (8)
. (8)
Соотношения для векторного произведения удобно выразить в матричной форме в виде определителя (детерминанта), что делает лёгким его запоминание
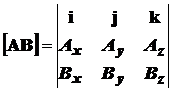 . (9)
. (9)
Если развернуть этот детерминант в соответствии с обычными правилами, то он окажется идентичным с уравнением (8).
Векторное произведение двух векторов само является вектором, поэтому можно найти его произведение на какой-то другой вектор. При этом второе умножение может соответствовать либо скалярному, либо векторному произведению, т.е. [AB]×C или [[AB]C]. Очевидно, что эти произведения различны и должны быть рассмотрены отдельно.
Если А, В и С являются какими-то тремя векторами, как показано на рис. 3, то тройное скалярное произведение [AB]×C даёт скалярную величину, равную объёму параллелепипеда, в котором А, В и С образуют рёбра.
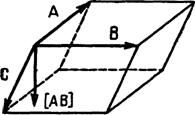
Рис. 3 – Геометрический смысл смешанного тройного произведения векторов
Это становится очевидным, если учесть, что векторное произведение [АВ] дает площадь верхушки параллелепипеда, а смешанное произведение [AB]C является произведением этой площади на нормальную компоненту ребра С. Объём того же самого параллелепипеда можно определить, умножая площадь, ограниченную векторами В и С, на нормальную компоненту А, так что [AB]C =[BC]Aи аналогично каждое из этих произведений равно [CA]B.
В свою очередь, результатом тройного векторного произведения [A[BC] является вектор, который, как следует из рис. 3, лежит в той же плоскости, что и векторы А и В. Его можно развернуть через скалярные произведения векторов в виде формулы Лагранжа следующим образом:
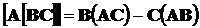 . (10)
. (10)
Доказательство этого положения Лагранжа может быть легко выполнено, если выразить обе части выражения через компоненты (проекции) по осям прямоугольных координат. Запомнить формулу Лагранжа можно по мнемоническому правилу «бац минус цаб».
Интегральные характеристики векторных полей
Векторным полем называется часть пространстваV (или все пространство), в каждой точке M ÎV которого задано какое-либо физическое явление, характеризуемое векторной величиной 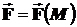 – силой поля. В общем случае векторное поле принимает разные значения в разных точках пространства. В каждой точке пространства вектор поля имеет определенную величину (модуль) и определенное (за исключением тех случаев, когда поле обращается в ноль) направление в этом пространств.
– силой поля. В общем случае векторное поле принимает разные значения в разных точках пространства. В каждой точке пространства вектор поля имеет определенную величину (модуль) и определенное (за исключением тех случаев, когда поле обращается в ноль) направление в этом пространств.
Если в пространстве V введена декартова прямоугольная система координат, то задание вектор-функции поля 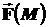 cводится к заданию трех скалярных функций:
cводится к заданию трех скалярных функций:
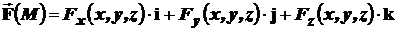 . (11)
. (11)
Простейшими геометрическими характеристиками векторных полей являются векторные линии и векторные трубки.
Векторными линиями поля 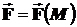 называются линии (кривые), в каждой точке Mкоторых направление касательной совпадает с направлением поля в этой точке. Векторной трубкой называется поверхность, образованная векторными линиями, проходящими через точки некоторой лежащей в поле замкнутой кривой C, не совпадающей (хотя бы и частично) с какой – либо векторной линией. Пример векторной трубки, образованной площадкой с замкнутой кривой С1, в которой векторные линии, проходящие через С1 целиком лежат внутри трубки, изображен на рис. 4.
называются линии (кривые), в каждой точке Mкоторых направление касательной совпадает с направлением поля в этой точке. Векторной трубкой называется поверхность, образованная векторными линиями, проходящими через точки некоторой лежащей в поле замкнутой кривой C, не совпадающей (хотя бы и частично) с какой – либо векторной линией. Пример векторной трубки, образованной площадкой с замкнутой кривой С1, в которой векторные линии, проходящие через С1 целиком лежат внутри трубки, изображен на рис. 4.

Рис. 4 – Векторная трубка
Если поле задано формулой (11), то уравнение векторных линий дается системой дифференциальных уравнений
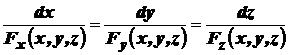 . (12)
. (12)
Методы решения этой системы (12) рассматриваются в теории дифференциальных уравнений.
Векторное поле  называется плоским, если в специально подобранной системе координат оно имеет вид:
называется плоским, если в специально подобранной системе координат оно имеет вид:
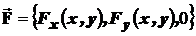 . (13)
. (13)
Система уравнений (12) для таких полей имеет вид
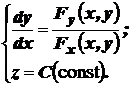 (14)
(14)
Таким образом, векторные линии плоского поля – это кривые, лежащие в плоскостях, параллельных плоскости OXY.
При расчете и анализе электромагнитных полей используют интегралылинейные (по кривой линии), а также интегралы по объему и по поверхности, ограничивающей этот объем. С помощью этих интегралов определяются интегральные (макроскопические) характеристики поля: циркуляция и поток, т.е. характеристики, наглядно описывающие поле в некотором конечном объеме или линейном участке пространства.
Поток векторного поля. Сила векторного поля в некотором объеме пространства может быть измерена количеством силовым линий, пронизывающих поверхность, ограничивающую этот объем. При этом совокупность силовых линий, пронизывающих некоторую поверхность по аналогии с гидродинамикой принято называть потоком поля.
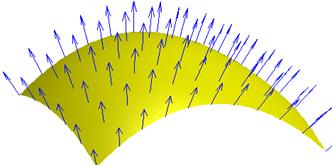
Введем понятие потока векторного поля и его математическое описание. Пусть в некоторой области пространства V, в которой определено векторное поле  , имеется односторонняя ориентированная поверхность S, на которой расположено поле единичных положительных нормалей
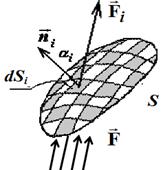
, имеется односторонняя ориентированная поверхность S, на которой расположено поле единичных положительных нормалей 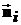 (см. рис. 5). Разобьем эту поверхность, как на рис. 5 б, на бесконечно малые кусочно-гладкие площадки площадью dSi, через каждую из которые проходит только одна силовая линия поля
(см. рис. 5). Разобьем эту поверхность, как на рис. 5 б, на бесконечно малые кусочно-гладкие площадки площадью dSi, через каждую из которые проходит только одна силовая линия поля  . Умножив вектор нормали
. Умножив вектор нормали 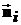 к точке i пространства на скалярную величину dS, получим вектор
к точке i пространства на скалярную величину dS, получим вектор 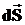 элементарной площадки.
элементарной площадки.
а) б)
Рис. 5 – Пояснение потока векторного поля
Тогда количество силовых линий поля, пересекающих элементарную площадку dSi, определятся скалярным произведением векторов, т.е.
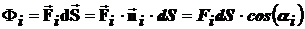 , (15)
, (15)
где 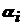 - угол в точки i между вектором нормали
- угол в точки i между вектором нормали 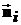 и вектором поля
и вектором поля 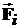 .
.
Добавляя к поверхности S вторую отрицательно ориентированную сторону и обобщая выражение (15) на всю двухстороннюю поверхность S, просуммировав по всем элементарным площадкам, получаем поток векторного поля
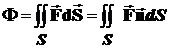 . (16)
. (16)
Таким образом, поток векторного поля  через двустороннюю ориентированную поверхность Sопределяется поверхностным интеграломпервого рода по поверхностиS от скалярного произведения вектора нормали к выбранной поверхности и вектора-функции поля. В случае замкнутой поверхности ее ориентируют, направляя нормаль изнутри области (V) наружу. Сторона с положительным направлением нормали называется положительной стороной поверхности.
через двустороннюю ориентированную поверхность Sопределяется поверхностным интеграломпервого рода по поверхностиS от скалярного произведения вектора нормали к выбранной поверхности и вектора-функции поля. В случае замкнутой поверхности ее ориентируют, направляя нормаль изнутри области (V) наружу. Сторона с положительным направлением нормали называется положительной стороной поверхности.
Существует другая форма записи поверхностного интеграла. Если связать вектор 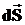 элементарной площадки с проекциями поверхности S на координатные плоскости через направляющие косинусы в следующем виде:
элементарной площадки с проекциями поверхности S на координатные плоскости через направляющие косинусы в следующем виде:
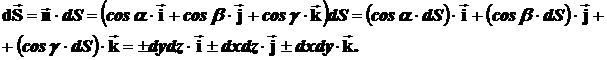
Если использовать координатную запись 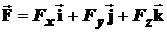 , то скалярное произведение в координатной форме примет вид
, то скалярное произведение в координатной форме примет вид
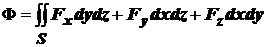 . (17)
. (17)
Это означает, что поток векторного поля может быть выражен и через поверхностный интеграл второго рода. В этом случае интегрирование производится по проекциям на координатные плоскости. В таком интеграле необходимо выбирать знак каждого слагаемого в зависимости от знака соответствующей координаты нормали.
Поток имеет все свойства поверхностного интеграла, при этом наиболее существенными являются:
- линейность, т.е. суммарный поток от нескольких векторных полей равен сумме потоков, создаваемых каждым полем в отдельности;
- аддитивность, т.е. если область V разделить произвольным образом на несколько элементарных областей, каждая из которыхограниченна локальной замкнутой поверхностью, то поток вектора через внешнюю поверхность равен сумме потоков через локальные замкнутые поверхности;
- поток меняет знак при изменении стороны поверхности, так как меняется ориентация единичных нормалей.
Физическая интерпретация заключается в том, что поток векторного поля, проходящий сквозь замкнутую поверхность, определяет количество жидкости, протекающей в единицу времени через эту поверхность в положительном направлении (отсюда общий термин «поток»).
Таким образом, установлено, что поток векторного поля определяет его величину (силу) в замкнутом объеме V ограниченном поверхностью S, следовательно, служит одновременно некоторым «индикатором» наличия поля в данной области пространства.
Циркуляция векторного поля. Термин циркуляция позаимствован из гидродинамики, в которой он использовался для расчета движения жидкости по замкнутому каналу. Рассмотрим сущность этой характеристики в рамках теории ЭМП. Пусть некоторой в области пространства V имеется векторное поле 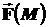 , отграничим эту области гладкой непрерывной линией (кривой) L. Представим, что к каждой точке M кривой L проведен единичный касательный (тангенциальный) вектор
, отграничим эту области гладкой непрерывной линией (кривой) L. Представим, что к каждой точке M кривой L проведен единичный касательный (тангенциальный) вектор  по заданному направлению обхода (правому или левому, как показано на рис. 6). Ориентация кривой L в пространстве V таково, что между вектором поля
по заданному направлению обхода (правому или левому, как показано на рис. 6). Ориентация кривой L в пространстве V таково, что между вектором поля 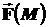 и вектором
и вектором  имеется угол a(M).
имеется угол a(M).

Рис. 6 – Пояснение циркуляции векторного поля
Введем характеристику поля, отражающую его интенсивность и направленность по отношению к точкам кривой L. Такой характеристикой для конкретной точки поля M служить скалярное произведение вектора-функции 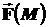 на некоторое бесконечно малое направление
на некоторое бесконечно малое направление 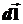 , совпадающее с единичным касательным вектором
, совпадающее с единичным касательным вектором  (см. рис. 6), т.е.
(см. рис. 6), т.е.
 . (18)
. (18)
Данная характеристика, представляет собой элементарную работу, совершаемую силой поля при перемещении точки вдоль произвольного контура L на малое расстояние dl. Например, работа электрического поля по перемещению единичного заряда.
Тогда обобщая на замкнутую кривую и применяя линейное интегрирование, получим циркуляцию векторного поля:
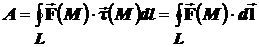 . (19)
. (19)
Таким образом, в теории ЭМП циркуляцией называется линейный интеграл векторного поля первого рода по замкнутой ориентированной кривой. Физический смысл циркуляции заключается в подсчете работы сил поля при перемещении материальной точки вдоль линии L.
Как и поток, циркуляцию можно представить иным образом. С учетом того, что произведение единичного касательного вектора 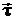 на перемещение dl даёт изменение (приращение) радиуса-вектора точки M, т.е.
на перемещение dl даёт изменение (приращение) радиуса-вектора точки M, т.е. 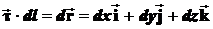 , тогда циркуляция равна:
, тогда циркуляция равна:
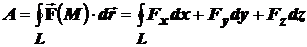 . (20)
. (20)
Следовательно, циркуляция может быть выражена и через криволинейный интеграл второго рода по координатам.
Циркуляция, как криволинейный интеграл, обладает следующими свойствами:
1) аддитивность, т.е. циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности;
2) меняет знак при изменении направления вдоль кривой L, это следует из того, что вектор  меняется на противоположенный, т.е. на
меняется на противоположенный, т.е. на 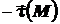 ;
;
3) знак работы зависит от направленности движения и сил поля, если векторы  коллинеарные, то работа А>0.
коллинеарные, то работа А>0.
Обычно говорят, что циркуляция характеризует вращательную способность поля. Имеется в виду следующее. Если векторные линии поля замкнуты, то, циркуляция по ним в направлении поля положительна, при этом в гидродинамической интерпретации частицы жидкости крутятся по этим замкнутым линиям. Из данного представления становиться ясно, что именно циркуляция жидкости заставляет вращаться гребное колесо (турбину) (см. рис. 7). Пусть теперь линии тока произвольны, вообразим в объёме V замкнутый контур L. Если в результате движения жидкости этот контур будет вращаться, то поле обладает вращательной способностью, абсолютная величина циркуляции будет определять угловую скорость вращения (чем больше циркуляция, тем выше скорость), а ее знак покажет, совпадает ли направление вращения с направлением интегрирования.

Рис. 7 – Пример образования и физический смысл циркуляции
Итак, если векторное поле является силовым, то циркуляция численно равна работе силового поля по замкнутому контуру.
В теории электромагнитного поля циркуляция выступает в качестве критерия потенциальности векторного поля. Если циркуляцияполя (совершаемая им работа) численно равна нулю, то такие поля называются консервативными или потенциальными, например электростатическое поле, гравитационное поле. В противном случае, когда циркуляция не равна нулю, поля называют вихревыми. Примером вихревых полей являются переменные электрические и магнитные поля. Более подробно данный критерий будет рассматриваться в последующих лекциях.
Итак, циркуляция поля представляет собой меру векторного поля, отражающею его интенсивность и направленность, характеризующая работу поля по замкнутому контуру, а также является критерием потенциальности поля.
Дата добавления: 2018-05-12; просмотров: 1203; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
