Переходные и частотные характеристики.
Переходные характеристики находят, решая уравнения динамики системы (элемента системы) при подаче на вход соответствующего возмущения при заданных начальных условиях.
Динамические свойства линейных САУ могут быть описаны не только уравнениями, но и графическими характеристиками. В ТАУ применяются два типа таких характеристик – переходные и частотные. В условиях реальной эксплуатации САУ часто возникает необходимость определить реакцию на периодические сигналы, т.е. определить сигнал на выходе САУ, если на один из входов подается периодически сигнал гармонической формы. Для этого используют частотные характеристики. Частотные характеристики могут быть получены экспериментальным или аналитическим путем.
Рисунок 37
Таким образом, частотные характеристики описывают установившиеся вынужденные колебания на выходе, вызванные гармоническим воздействием на входе.
Если на ввод подано гармоническое воздействие
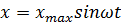, (50)
Где 
– амплитуда, 
– угловая частота этого воздействия. По окончании переходного процесса на выходе будут существовать гармонические колебания с той же частотой, что и входные колебания, но отличающиеся в общем случае по амплитуде и фазе
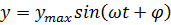(51)
Здесь 
– амплитуда выходных установившихся колебаний, 
– фазовый сдвиг между выходными и входными колебаниями.
|
|
|
При фиксированной амплитуде входных колебаний амплитуда и фаза установившихся колебаний на выходе зависят от частоты колебаний. Если постепенно увеличивать от нуля частоту колебаний и определять установившиеся значения амплитуды и фазы выходных колебаний для разных частот, можно получить зависимость от частоты отношения амплитуд
(52)
и сдвига фаз выходных и входных установившихся колебаний. Эти зависимости называются соответственно 
- амплитудно-частотной характеристикой (АЧХ) и 
–фазо-частотной характеристикой (ФЧХ). Амплитудную и фазовую частотные характеристики можно объединить в одну амплитудно-фазовую частотную характеристику (АФЧХ), используя и в качестве полярных координат. АФЧХ можно строить и в прямоугольной системе координат – в комплексной плоскости.
Переходная или временная характеристика (функция) представляет собой реакцию на выходе, вызванную подачей на вход ступенчатого воздействия.
Единичное ступенчатое воздействие (единичная ступенчатая функция, функция включения Хевисайда) – это воздействие (рисунок 38), которое мгновенно возрастает от нуля до единицы и далее остается неизменным.
|
|
|
Единичное ступенчатое воздействие обозначается 1(t) и может быть описано следующим равенством:
Рисунок 38
При ступенчатом изменении функции на произвольную величину А, отличную от единицы, используют произведение 
.
Примером ступенчатого воздействия может явиться воздействие, оказываемое на систему регулирования напряжения резким сбросом или подключением нагрузки на генератор.
Наряду с переходной характеристикой применяется импульсная переходная (временная) характеристика или функция, называемая весовой функцией (функция веса). Эта характеристика представляет собой реакцию на единичный импульс. Единичный импульс (единичная импульсная функция или дельта-функция) – это математическая идеализация предельно короткого импульсного сигнала. Единичный импульс – это импульс, площадь которого равна единице при длительности равной нулю и высоте равной бесконечности.
Единичная импульсная функция 
(дельта - функция Дирака) обозначает бесконечно короткий (по длительности) и бесконечно большой по амплитуде импульс с единичной площадью:
|
|
|
= 
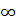при t=0 и 
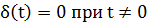при этом согласно определению
(53)
Импульсная переходная характеристика обозначается w(t), а единичный импульс – δ(t). Таким образом,
w(t) – это y(t) при x(t) = δ(t). Математически дельта-функция записывается так:
(54)
Функцию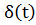 
можно представить как предельное значение прямоугольного импульса (рисунок 39) с длительностью 
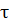и амплитудой 
при 
, при этом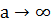 
, 
.
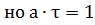Практически за импульсные воздействия можно принимать воздействия, сообщающие системе за время, значительно меньшее продолжительности переходного процесса, конечное количество энергии.
Рисунок 39
Дельта-функцию можно определить и как производную от единичного ступенчатого воздействия : 
(55)
Дельта-функция просто связана с единичной ступенчатой функцией:
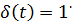- единичная ступенчатая функция; Отсюда следует, что весовая функция является первой производной переходной функции.
Гармоническая функция описывает величины, изменяющиеся во времени по гармоническому закону (рисунок 40).
|
|
|
Вещественная форма записи гармонической функции:
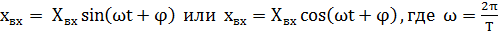(56)
– амплитуда,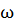 
– круговая частота, 
– начальная фаза,
– период колебаний.
Рисунок 40
Реакция объекта на единичный скачок называется переходной функцией (переходной характеристикой) и обозначается h(t).Таким образом, h(t) – это выражение для y(t) при x(t)=1(t).
Переходная функция показывает, как изменяется во времени выходная величина при подаче на вход единичного возмущающего воздействия. То есть, переходной функцией называется реакция предварительно невозбужденного устройства на единичное ступенчатое воздействие (предполагается, что объект в начальный момент времени находится в состоянии покоя, то есть все переменные состояния равны нулю и внутренняя энергия также нулевая).
Импульсной функцией (импульсной характеристикой) g(t) называется реакция предварительно невозбужденного устройства на единичное импульсное воздействие 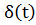. Часто импульсную функцию называют функцией веса.
Дата добавления: 2018-05-12; просмотров: 1753; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!