Симплекс метод с алгебраическими преобразованиями

Министерство образования и науки Российской Федерации

ФГБОУ ВО «Тульский государственный университет»

Технический колледж им. С.И. Мосина

 

Курсовая работа

По дисциплине «Математическое моделирование»

На тему: «Реализация симплекс-метода при отрицательных свободных членах»

 

 

 

Выполнил,

студент гр. 3-090203                                                                 УльяненкоС.С.

 

Проверил:                                                                    Воронцова Н.В.

 

 

Тула 2018

I. Теоретическая часть.

Общая постановка задачи.

 

Симплексный метод – это вычислительная процедура, основанная на принципе последовательного улучшения решений при переходе от одной базисной точки (базисного решения) к другой. При этом значение целевой функции улучшается.

Базисным решением является одно из допустимых решений, находящихся в вершинах области допустимых значений. Проверяя на оптимальность вершину за вершиной симплекса, приходят к искомому оптимуму. На этом принципе основан симплекс-метод.

Симплекс – это выпуклый многоугольник в n-мерном пространстве с n+1 вершинами, не лежащими в одной гиперплоскости (гиперплоскость делит пространство на два полупространства).

Например, линия бюджетных ограничений делит блага на доступные и недоступные.

Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число итераций (шагов), кроме случаев «зацикливания».

Суть симплекс-метода заключается в направленном переборе вершин ОДР с целью определения координат такой вершины, в которой целевая функция достигает экстремума. Введем несколько определений.

Опорным решением системыограничений называется такое решение, когда для системы ограничений в допустимом каноническом виде все свободные переменные равны нулю.

Вырожденное опорное решение-опорное решение, в котором одна или несколько базисных переменных равны нулю.

Допустимое опорное решение-опорное решение, в котором все базисные переменные≥ 0.

Решение симплекс-метода табличным методом

 

Оптимальное решение ЗЛП будет соответствовать одному из допустимых опорных решений. В симплекс-методе, начиная с допустимого опорного решения, расположенного в вершине многогранника ОДР, переходят к соседней вершине, сохраняя допустимость решения.

Для удобства формулировки правил метода запишем допустимую каноническую форму ЗЛП в ином виде, называемом стандартной формой. Например:

;

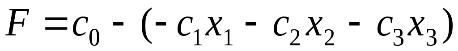Для упрощения реализации симплекс-метода на ЭВМ его представляют в табличной форме. В этом случае каждое опорное решение соответствует новой симплекс-таблице. Каждая строка таблицы соответствует либо строке целевой функции, либо строке одного из ограничений. Пример таблицы для случая семи переменных для стандартной формы записи приведен ниже.

свободн. член x1 x2 x3 F c0 -c1 -c2 -c3 x4 b1 a11 a12 a13 x5 b2 a21 a22 a23 x6 b3 a31 a32 a33 x7 b4 a41 a42 a43

В симплекс-таблице вводится понятие разрешающего элемента -элемента, лежащего на пересечении разрешающего столбца (соответствующего новой базисной переменной) и разрешающей строки (соответствующей новой свободной переменной) при процедуре замены базиса. Замена базиса необходима для перехода к следующему опорному решению.

В симплекс-методе требуется иметь исходное допустимое опорное решение. Иногда такое решение получить легко. Например, если существует ограничение вида с положительной правой частью, то дополнительные переменные, используемые при записи ограничений в виде равенств, образуют допустимое опорное решение, в котором все переменные проектирования равны нулю, а дополнительные переменные являются базисными. Однако во многих задачах существуют ограничения вида³0 и = 0, для которых начальное опорное решение может быть недопустимым. Поэтому применению симплекс-метода в общем случае должен предшествовать этап поиска допустимого решения. Рассмотрим один из вариантов алгоритма симплекс-метода с учетом этапа поиска допустимого решения.

Алгоритм симплекс-метода

1-й этап:нахождение допустимого опорного решения.

Шаг 1.Ограничения неравенства приводятся к виду ограничений ра-венств. Задача записывается в стандартной форме.

Шаг 2.Для каждого ограничения, имеющего отрицательный свободный член, просматриваются знаки коэффициентов при свободных переменных. Если отсутствует хотя бы один отрицательный коэффициент, то ограничения несовместны. Если во всех ограничениях свободные члены неотрицательны, то опорное решение является допустимым и необходимо переходить ко второму этапу (этапу нахождения оптимального решения).

Шаг 3.Для ограничения, имеющего отрицательный свободный член, выбирается свободная переменная с отрицательным коэффициентом. Эта переменная будет новой базисной переменной. Если отрицательных коэффициентов более одного, то в качестве новой базисной переменной можно выбрать любую, имеющую отрицательный коэффициент (выбор переменной в этом случае скажется на числе замен базиса, но не на конечном результате). Пусть это будет переменнаяx_l. Если ограничений с отрицательным свободным членом более одного, то можно для анализа коэффициентов выбрать любое.

Шаг 4.Для выбора новой свободной переменной рассматривается отношениеb_j/a_jlдля всех ограничений, причемb_jиa_jlдолжны иметь одинаковый знак. Находится минимальное отношение. Новой свободной переменной будет та базисная переменная, для ограничения которой отношениеb_j/a_jlоказалось минимальным. В этом случае разрешающий элемент таблицы будет находиться на пересечении столбца, соответствующего переменнойx_lи строки, соответствующей ограничению, для которого получено минимальное отношение.

Шаг 5.Делается замена базиса. Для пересчета значений элементов симплекс-таблицы после смены базиса введем в таблицу следующие обозначения:

Своб. член x1 x2 ... xi F a11 a12     a1l xi+1 a21 a22     a2l ... ... ... ... ... ... xn ak1 ak2     akl

С учетом введенных обозначений после смены базиса все элементы таблицы могут быть пересчитаны по следующим выражениям с учетом того, что arp-разрешающий элемент (r, q -строка,p, s -столбец).

при q=r; s=p,n-номер итерации(смены базиса);

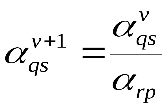при q=r;s p, s= ;

при q r;s=p;q= ;

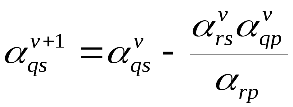для остальных элементов.

Шаг 6. Возвращаемся на шаг 2.

2-й этап:нахождение оптимального решения.

Шаг 1.Проверяется признак оптимальности решения.

Признаки оптимального решения:

а) целевая функция будет иметь максимальное значение в том случае, когда в строке (выражении) целевой функции в стандартной форме записи все коэффициенты при свободных переменных положительны (свободный член не рассматривается);

б) целевая функция будет иметь минимальное значение в том случае, если в строке целевой функции в стандартной форме все коэффициенты при свободных переменных отрицательны;

в) если в выражении целевой функции в стандартной форме все коэффициенты при переменных одного знака и при этом есть хотя бы один нулевой коэффициент, то полученное решение является альтернативным, т. е. будет другой набор переменных, доставляющих целевой функции такое же значение.

Если признак оптимальности выполняется, то решение найдено. Значения свободных переменных равны нулю, значения базисных переменных равны свободным членам соответствующих ограничений, значение целевой функции равно свободному члену целевой функции. Если признак оптимальности не выполняется, то переходим к шагу 2.

Шаг 2.В соответствии с правилом выбора новой базисной переменной одну из свободных переменных переводим в базисные.

Правило выбора свободной переменной, переводимой в базис

При поиске максимума (минимума) функции, записанной в стандартной форме, в базис должна переводиться переменная, имеющая отрицательный (положительный) коэффициент в выражении целевой функции в стандартной форме. Если имеется более одного отрицательного (положительного) коэффициента c_j, то выбирают переменную, имеющую больший по абсолютной величине отрицательный (положительный) коэффициентc_j.

Шаг 3.В соответствии с правилом выбора переменной, переводимой из базисной в свободные, определяем новую свободную переменную.

Сформулируем правило выбора переменной, переводимой из базисных в свободные.

Для выбора новой свободной переменной x_iнеобходимо рассмотреть отношениеb_j /a_ijдля всех ограничений ( 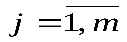), ( ), 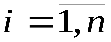из этих отношений выбрать минимальное, а в качестве новой свободной переменной выбирать базисную переменную, для ограничения которой получено минимальное отношениеb_j /a_ij. Отношениеb_j/a_ijнеобходимо рассматривать только для положительныхa_ij. Если минимум достигается более чем для одного индексаj, то из базиса исключается любая из переменных, соответствующихj-м ограничениям.

Если ни один из a_ijне является положительным, то получение нового допустимого решения невозможно, т.е. при поиске минимума целевая функция не ограничена снизу, а при поиске максимума-не ограничена сверху (признак неограниченности целевой функции).

Шаг 4.Осуществляется замена базиса аналогично шагу 5 первого этапа.

Шаг 5.Переходим к шагу 1.

2 практияеская часть

2.1 постаноская задачи

Пример 2.Найти при ограничениях

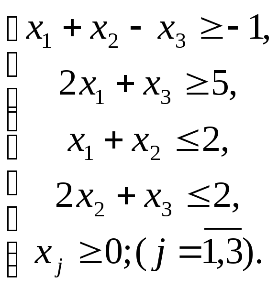
Введем дополнительные переменные и перейдем в ограничениях к знакам “=”.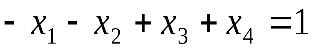

; ; ; ; , .

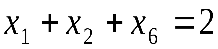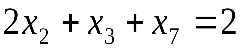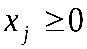Запишем задачу в стандартной форме и представим ее в виде симплекс-таблицы:

;	Cв. чл. x1 x2 x3 F 0 -2 2 1 x4 1 -1 -1 1 x5 -5 -2 0 -1 x6 2 1 1 0 x7 2 0 2 1

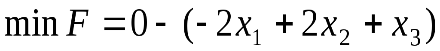
Признак несовместности ограничений не выполняется. Допустимое решение не найдено, так как свободный член для ограничения x₅равен-5. Для получения допустимого решения произведем смену базиса. В качестве разрешающего столбца выберемx₁; разрешающей строки –x₆(так как 2/1 <-5/-2). Разрешающий элемент подчеркнут. Строим новую симплекс-таблицу.

 

 

	Cв. чл. x6 x2 x3   F 4 2 4 1 x4 3 1 0 1 x5 -1 2 2 -1 x1 2 1 1 0 x7 2 0 2 1					Допустимое реше-ние не найдено. Произведем сле-дующую замену базиса.	Cв. чл. x6 x2 x5 F 3 4 6 1 x4 2 3 2 1 x3 1 -2 -2 -1 x1 2 1 1 0 x7 1 2 4 1
	Cв. чл.	x2	x7	x5
F	1	-2	-2	-1
x4	1/2	-4	-3/2	-1/2
x3	2	2	1	0
x1	3/2	-1	-1/2	-1/2
x6	1/2	2	1/2	1/2

	Cв. чл.	x6	x7	x5
F	3/2	1	-3/2	-1/2
x4	3/2	2	-1/2	½
x3	3/2	-1	½	-1/2
x1	7/4	1/2	-1/4	-1/4
x2	1/4	1/2	¼	¼

 

 

Признак оптимальности удовлетворяется. Решение задачи:

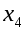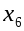min F=1; =3/2; =0; =2; =1/2; =0; =1/2;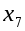

 

Симплекс метод с алгебраическими преобразованиями

 

Решим алгебраическими преобразованиями тот же пример, что и в предыдущем параграфе. Следует отметить, что при решении этой разновидностью симплекс метода лучше не записывать функцию цели в виде 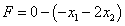, так как при этом легко запутаться в знаках. Но в этом случае пункт алгоритма, определяющий критерий оптимальности, будет модифицирован следующим образом.

Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с положительными (отрицательными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным - решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с положительными (отрицательными) коэффициентами, перейти к новому базисному решению.

Пример. Найти максимум функции 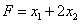при ограничениях

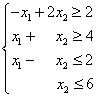
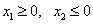
Решение.

Шаг I. Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений

.

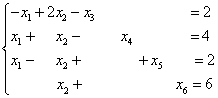
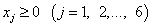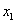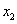Введённые добавочные переменные принимаем за основные, так как в этом случае базисное решение системы легко находится. Тогда и - неосновные переменные.

Выразив основные переменные через неосновные, получим

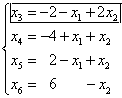
Следовательно, данному разбиению переменных на основные и неосновные соответствует базисное решение , которое является недопустимым (две переменные отрицательны), а поэтому оно не оптимальное. От этого базисного решения перейдём к улучшенному.

Чтобы решить, какую переменную следует перевести из неосновных в основные, рассмотрим любое из двух имеющихся уравнений последней системы с отрицательными свободными членами, например второе. Оно показывает, что в основные переменные можно перевест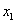и и 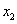, так как в этом уравнении они имеют положительные коэффициенты (следовательно, при их увеличении, а это произойдёт, если переведём любую из них в основные переменные, переменная увеличится).

Попробуем перевести в основные переменную 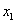. Чтобы установить, какую переменную следует перевести из основные в неосновные, найдём абсолютную величину наименьшего отношения свободных членов системы к коэффициентам при 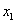. Имеем 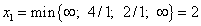. Оно получено из третьего уравнения, показывающего, что в неосновные нужно перевести переменную 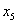, которая в исходном базисном решении положительна. Следовательно, полученное базисное решение, как и исходное, содержит две отрицательные компоненты, т. е. при переходе к такому базисному решению улучшения не произойдёт.

Если же перевести в основные переменную 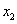, то наименьшее отношение свободных членов к коэффициентам при 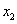составит 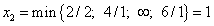. Оно получено из первого уравнения, в котором свободный член отрицателен. Следовательно, переводя 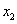в основные, а в неосновные переменные, мы получим базисное решение, в котором число отрицательных компонент на единицу меньше, чем в исходном. Поэтому остановимся на этой возможности: переводим 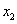в основные, а в неосновные переменные. Поэтому в приведённой выше системе уравнений выделенным оказалось первое уравнение.

Шаг II.

Основные переменные 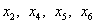, неосновные переменные .

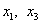Выразим новые основные переменные через новые неосновные, начиная с выделенного на шаге I уравнения. В результате получим

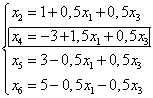
Следовательно, имеем новое базисное решение 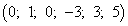, которое также является недопустимым, а поэтому не оптимальным. Но в нём, как мы и предвидели, только одна переменная отрицательна (а именно ).

От полученного базисного решения необходимо перейти к другому. Рассмотрим уравнение с отрицательным свободным членом, т. е. второе уравнение. Оно показывает, что в основные переменные можно перевест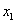и и . Переведём в основные переменные 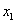. Найдём наименьшее из абсолютных величин отношений свободных членов системы к коэффициентам при 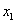. Имеем 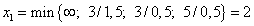. Значит, в неосновные переменные нужно перенести . Так как наименьшее отношение получено из второго уравнения, то его выделяем. В новом базисном решении уже не окажется отрицательных компонент, т. е. оно является допустимым.

В особых случаях решение завершается на II шаге: это, например, случаи, когда максимум целевой функции - бесконечность и когда система не имеет ни одного решения.

Шаг III.

Основные переменные: 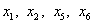, неосновные переменные: . Выразив основные переменные через неосновные, получим

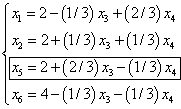
Новое базисное решение имеет вид 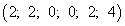. Является ли оно оптимальным, можно установить, если выразить линейную форму через неосновные переменные рассматриваемого базисного решения. Сделав это, получим 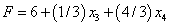. Так как мы ищем максимум линейной формы, а нашли лишь одно допустимое решение, то продолжим перебор.

Переводим в число основных переменную , имеющую больший положительный коэффициент. Находим 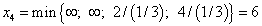. Это наименьшее отношение получено из третьего уравнения системы, поэтому его выделяем. Оно показывает, что при 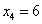переменная 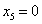и поэтому перейдёт в число неосновных.

В некотором особом случае решение завершается на III шаге: это случай, когдаоптимальное решение - не единственное.

Шаг IV.

Основные переменные: 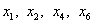, неосновные переменные: 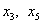. Выразив основные переменные через неосновные, получим

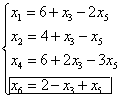
Линейная форма, выраженная через те же неосновные переменные, примет вид 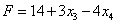. Продолжим перебор для поиска максимума.

Увеличение линейной формы возможно при переходе к новому базисному решению, в котором переменная является основной. Находим 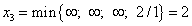. Это наименьшее отношение получено из четвёртого уравнения системы и показывает, что при переменная 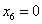и переходит в число неосновных.

Шаг V.

Основные переменные: 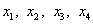, неосновные переменные: . Выразив основные переменные через неосновные, получим

Линейная форма, выраженная через неосновные переменные нового базисного решения, имеет вид . Критерий оптимальности для случая максимизации линейной формы выполнен. Следовательно, базисное решение 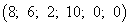является оптимальным, а максимум линейной формы

 

Приложение

 

using System;

usingSystem.Collections.Generic;

usingSystem.Linq;

usingSystem.Text;

usingSystem.Threading.Tasks;

 

namespace Simplex

{

public class Simplex

{

   //source - симплекстаблицабезбазисныхпеременных

double[,] table; //симплекстаблица

 

int m, n;

 

List<int>basis; //список базисных переменных

 

public Simplex(double[,] source)

   {

       m =source.GetLength(0);

       n = source.GetLength(1);

table = new double[m, n + m - 1];

basis = new List<int>();

 

for (inti = 0; i< m; i++)

{

for (int j = 0; j <table.GetLength(1); j++)

{

if (j < n)

table[i, j] = source[i, j];

else

table[i, j] = 0;

           }

           //выставляем коэффициент 1 перед базисной переменной в строке

if ((n + i) <table.GetLength(1))

           {

table[i, n + i] = 1;

basis.Add(n + i);

}

       }

 

       n = table.GetLength(1);

   }

 

   //result - в этот массив будут записаны полученные значения X

public double[,] Calculate(double[] result)

   {

intmainCol, mainRow; //ведущиестолбецистрока

 

while (!IsItEnd())

       {

mainCol = findMainCol();

mainRow = findMainRow(mainCol);

basis[mainRow] = mainCol;

 

double[,] new_table = new double[m, n];

 

for (int j = 0; j < n; j++)

new_table[mainRow, j] = table[mainRow, j] / table[mainRow, mainCol];

 

for (inti = 0; i< m; i++)

{

if (i == mainRow)

continue;

 

for (int j = 0; j < n; j++)

new_table[i, j] = table[i, j] - table[i, mainCol] * new_table[mainRow, j];

}

table = new_table;

       }

 

       //заносим в result найденные значения X

for (inti = 0; i<result.Length; i++)

       {

int k = basis.IndexOf(i + 1);

if (k != -1)

result[i] = table[k, 0];

else

result[i] = 0;

       }

 

return table;

   }

 

private bool IsItEnd()

   {

bool flag = true;

 

for (int j = 1; j < n; j++)

       {

if (table[m - 1, j] < 0)

           {

flag = false;

break;

           }

       }

 

return flag;

   }

 

privateintfindMainCol()

   {

intmainCol = 1;

 

for (int j = 2; j < n; j++)

if (table[m - 1, j] < table[m - 1, mainCol])

mainCol = j;

 

returnmainCol;

   }

 

privateintfindMainRow(intmainCol)

   {

intmainRow = 0;

 

for (inti = 0; i< m - 1; i++)

if (table[i, mainCol] > 0)

           {

mainRow = i;

break;

           }

 

for (inti = mainRow + 1; i< m - 1; i++)

if ((table[i, mainCol] > 0) && ((table[i, 0] / table[i, mainCol]) < (table[mainRow, 0] / table[mainRow, mainCol])))

mainRow = i;

 

returnmainRow;

   }

 

 

}

}

 

---

Дата добавления: 2018-05-12; просмотров: 1269; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!