ВАРИАНТЫ ОТВЕТОВ
1)  2)
2) 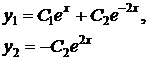
3)  4)
4) 
ВАРИАНТ № 3
ЗАДАНИЕ № 1.
Установите соответствие между номером уравнения и его типом
1)  2)
2) 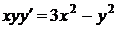
3) 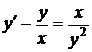 4)
4) 
___ уравнение с разделяющимися переменными,
___ однородное дифференциальное уравнение,
___ уравнение в полных дифференциалах,
___ уравнение Бернулли
___ уравнение, приводящееся к однородному.
ЗАДАНИЕ № 2.
Дано уравнение первого порядка 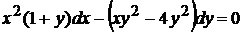 в форме, содержащей дифференциалы. Приведите его к виду, разрешенному относительно производной.
в форме, содержащей дифференциалы. Приведите его к виду, разрешенному относительно производной.
| Ответ |
ЗАДАНИЕ № 3.
Дано дифференциальное уравнение  тогда функция
тогда функция  является его решением при
является его решением при  равном:
равном:
| Ответ |
ЗАДАНИЕ № 4.
Общий интеграл дифференциального уравнения  имеет вид
имеет вид
ВАРИАНТЫ ОТВЕТОВ:
1)  2)
2) 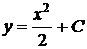 3)
3) 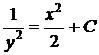 4)
4) 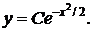
ЗАДАНИЕ № 5.
Укажите интегральную кривую решения задачи Коши для обыкновенного дифференциального уравнения 
ВАРИАНТЫ ОТВЕТОВ: 1) D 2) C 3) A 4) B
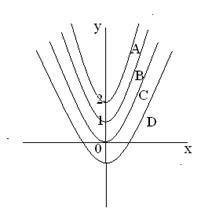
ЗАДАНИЕ № 6.
Дано дифференциальное уравнение второго порядка 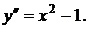 Тогда общее решение уравнения имеет вид
Тогда общее решение уравнения имеет вид
ВАРИАНТЫ ОТВЕТОВ:
1)  2)
2) 
3) 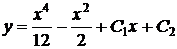 4)
4) 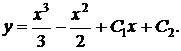
ЗАДАНИЕ № 7.
Решение задачи Коши 
 имеет вид
имеет вид
ВАРИАНТЫ ОТВЕТОВ:
1)  2)
2)  3)
3) 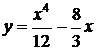 4)
4) 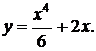
ЗАДАНИЕ № 8.
Дано дифференциальное уравнение второго порядка  тогда его общее решение имеет вид:
тогда его общее решение имеет вид:
| Ответ |
ЗАДАНИЕ № 9.
Дано дифференциальное уравнение второго порядка  тогда его общее решение имеет вид
тогда его общее решение имеет вид
ВАРИАНТЫ ОТВЕТОВ:
1)  2)
2)  3)
3) 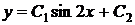
4) 
ЗАДАНИЕ № 10.
Корни характеристического уравнения равны:
 тогда фундаментальная система решений линейного однородного дифференциального уравнения будет иметь вид
тогда фундаментальная система решений линейного однородного дифференциального уравнения будет иметь вид
ВАРИАНТЫ ОТВЕТОВ:
1) 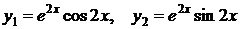
2) 
3) 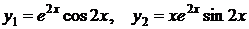
4) 
ЗАДАНИЕ № 11.
Корни характеристического уравнения равны  тогда общее решение линейного однородного дифференциального уравнения будет иметь вид:
тогда общее решение линейного однородного дифференциального уравнения будет иметь вид:
| Ответ |
ЗАДАНИЕ № 12.
Известна фундаментальная система решений однородного линейного дифференциального уравнения: 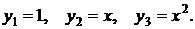 Тогда частное решение уравнения, удовлетворяющее начальным условиям
Тогда частное решение уравнения, удовлетворяющее начальным условиям
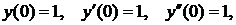 равно:
равно:
ВАРИАНТЫ ОТВЕТОВ:
1) 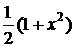 2)
2)  3)
3)  4)
4) 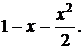
ЗАДАНИЕ № 13.
Дано линейное однородное дифференциальное уравнение с постоянными коэффициентами 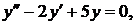 тогда его общее решение имеет вид:
тогда его общее решение имеет вид:
| Ответ |
ЗАДАНИЕ № 14.
Функция  является общим решением линейного однородного дифференциального уравнения с постоянными коэффициентами, тогда его характеристическое уравнение имеет вид
является общим решением линейного однородного дифференциального уравнения с постоянными коэффициентами, тогда его характеристическое уравнение имеет вид
ВАРИАНТЫ ОТВЕТОВ:
1) 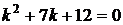 2)
2)  3)
3)  4)
4)  .
.
ЗАДАНИЕ № 15.
Частному решению линейного неоднородного дифференциального уравнения  по виду его правой части соответствует функция
по виду его правой части соответствует функция
ВАРИАНТЫ ОТВЕТОВ:
1) 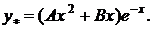 2)
2)  3)
3)  4)
4) 
ЗАДАНИЕ № 16.
Дано линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 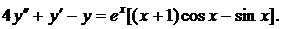 Записать вид частного решения с неопределенными коэффициентами
Записать вид частного решения с неопределенными коэффициентами
| Ответ |
ЗАДАНИЕ № 17.
Дано линейное неоднородное дифференциальное уравнение с постоянными коэффициентами  В каком виде следует искать частное решение неоднородного уравнения методом вариации произвольных постоянных ?
В каком виде следует искать частное решение неоднородного уравнения методом вариации произвольных постоянных ?
| Ответ |
ЗАДАНИЕ № 18.
Решение краевой задачи 
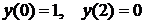 имеет вид
имеет вид
ВАРИАНТЫ ОТВЕТОВ:
1)  2)
2) 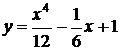 3)
3) 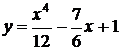 4)
4)  .
.
ЗАДАНИЕ № 19.
Дано дифференциальное уравнение  и начальное условие
и начальное условие  Тогда первые три члена разложения его решения в степенной ряд имеют вид
Тогда первые три члена разложения его решения в степенной ряд имеют вид
Дата добавления: 2018-05-12; просмотров: 857; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
