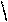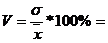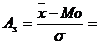Задача для самостоятельной работы
Дисциплина «Статистика»
Лабораторная работа №4
ТЕМА 3: СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ И ИХ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
Теоретическая часть
Статистическое описание совокупности было бы неполным, если ограничиваться лишь показателями центральной тенденции: средними величинами, модой и медианой, которые являются равнодействующими изменяющихся значений признака.
В одних случаях значение признака концентрируется возле некоторого центра тесно, в других случаях наблюдается значительное рассеивание, хотя средняя величина может быть одинаковой.
В связи с этим средняя величина не дает исчерпывающей характеристики изучаемой совокупности. Возникает необходимость изучения характера рассеивания признака (вариации признака).
Вариация наблюдается и в пределах однородной совокупности или однородной группы. Изучение вариации предполагает использование следующих приемов: построение вариационного ряда (ряда распределения), его графическое изображение и исчисление основных характеристик распределения. Вариационные ряды бывают дискретные и интервальные.
Дискретный ряд распределения — это ряд, в котором варианты выражены целым числом. Примером может служить распределение рабочих по тарифным разрядам:
| Тарифный разряд | Число рабочих, чел. |
| 1-й | 10 |
| 2-й | 20 |
| 3-й | 40 |
| 4-й | 60 |
| 5-й | 50 |
| 6-й | 20 |
| Всего | 200 |
Интервальный ряд распределения — это ряд, в котором значения признака заданы в виде интервала. Например, распределение рабочих по разрядам можно представить в виде интервального ряда:
| Тарифный разряд | Число рабочих, чел. |
| 1-2-й | 30 |
| 3-4-й | 100 |
| 5-6-й | 70 |
| Всего | 200 |
Для признака, имеющего прерывное изменение и небольшое количество значений, применяется построение дискретного ряда, который состоит из двух граф: значений признака и численности единиц с определенным значением признака, т. е. вариант и частот. Вариационный ряд иногда дополняют графами накопленных частот и частостей, рассчитанных путем деления частоты каждого интервала на их общую сумму.
ПОКАЗАТЕЛИ ВАРИАЦИИ (КОЛЕБЛЕМОСТИ) ПРИЗНАКА
Для характеристики размера вариации признака используются абсолютные и относительные показатели. К абсолютным показателям вариации относятся:
· размах колебаний;
· среднее линейное отклонение;
· среднее квадратическое отклонение;
· дисперсия;
Размах колебаний (размах вариации)
,
где 
, 
— соответственно максимальное и минимальное значения признака.
Величина показателя зависит от величины только двух крайних вариант и не учитывает степени колеблемости основной массы членов ряда.
Среднее линейное отклонение (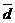 
) и среднее квадратическое отклонение ( 
) показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.
Среднее линейное отклонение определяется по формулам:
а) для несгруппированных данных (первичного ряда)
б) для вариационного ряда
Среднее квадратическое отклонение ( ) и дисперсия ( 
) определяются так:
а) для несгруппированных данных
;
;
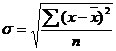б) для вариационного ряда
;
;
Формула для расчета дисперсии может быть преобразована:
,
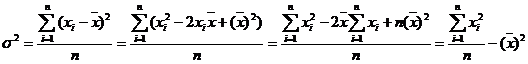т.е. дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины. Следовательно,
.
Среднее квадратическое отклонение по своей величине всегда превышает значение среднего линейного отклонения в соответствии со свойством мажорантности средних.
При сравнении вариации различных признаков в одной и той ж совокупности или же при сравнении вариации одного и того же признака в нескольких совокупностях с различной величиной средней арифметической используются относительные показатели вариации: коэффициент осцилляции, относительное отклонение, коэффициент вариации.
Наиболее объективным показателем является коэффициент вариации:
 |
который применяют не только для сравнения вариации, но и для характеристики однородности совокупности. Распределение считается близким к нормальному, а совокупность однородна, если коэффициент вариации не превышает 33%.
Для сравнительного анализа степени асимметрии нескольких распределений рассчитывается относительный показатель асимметрии (As):
Величина показателя асимметрии As может быть положительной и отрицательной. Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии. Отрицательный знак показателя асимметрии говорит о наличии левосторонней асимметрии. Чем больше абсолютная величина коэффициента, тем больше степень скошенности. Принято считать, что если коэффициент ассиметрии меньше 0,25 — ассиметрия незначительная, если свыше 0,5 — ассиметрия значительная.
Решение типовой задачи
| Задача 4.1 | |||||||||||||||||||||||||||||
| По приведенным ниже данным о квалификации рабочих цеха требуется: | |||||||||||||||||||||||||||||
| - построить дискретный ряд распределения; | |||||||||||||||||||||||||||||
| - дать графическое изображение ряда; | |||||||||||||||||||||||||||||
| - вычислить показатели центра распределения, показатели вариации и формы распределения. | |||||||||||||||||||||||||||||
| Тарифные разряды 24 рабочих цеха: | |||||||||||||||||||||||||||||
| 3 | 5 | 2 | 5 | 4 | 4 | 5 | 4 | 3 | 5 | 6 | 3 | 3 | 5 | 3 | 4 | 4 | 2 | 6 | 6 | 3 | 4 | 2 | 3 | ||||||
| Решение. | |||||||||||||||||||||||||||||
| 1. Дискретный ряд распределения имеет вид: | |||||||||||||||||||||||||||||
| Распределение рабочих цеха по квалификации | |||||||||||||||||||||||||||||
| Тарифный разряд, x | Число рабочих, f | Накопленная частота, S | |||||||||||||||||||||||||||
| 1 | 0 |
| |||||||||||||||||||||||||||
| 2 | 3 | 3 | |||||||||||||||||||||||||||
| 3 | 7 | 10 | |||||||||||||||||||||||||||
| 4 | 6 | 16 | |||||||||||||||||||||||||||
| 5 | 5 | 21 | |||||||||||||||||||||||||||
| 6 | 3 | 24 | |||||||||||||||||||||||||||
| 7 | 0 |
| |||||||||||||||||||||||||||
| Итого | 24 | — | |||||||||||||||||||||||||||
| 2. На рис. 4.1 представлено графическое изображение построенного дискретного вариационного ряда в виде полигона частот. | |||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
| Рис. 4.1. Полигон распределения рабочих цеха по квалификации | |||||||||||||||||||||||||||||
| Полигон частот замыкается, для этого крайние вершины соединяются с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе (в данном случае х = 1 и х = 7). | |||||||||||||||||||||||||||||
| 3. К показателям центра распределения относятся: средняя арифметическая, мода и медиана. | |||||||||||||||||||||||||||||
| Средняя арифметическая взвешенная - | |||||||||||||||||||||||||||||
|
| ∑x*f | = | 2 | * | 3 | + | 3 | * | 7 | + | 4 | * | 6 | + | 5 | * | 5 | + | 6 | * | 3 | = | |||||||
| ∑f | 3 | + | 7 | + | 6 | + | 5 | + | 3 | ||||||||||||||||||||
| = | 94 | = | 3,9 | разряда. | |||||||||||||||||||||||||
| 24 | |||||||||||||||||||||||||||||
| Мода - | |||||||||||||||||||||||||||||
| Мо = | 3 | -му разряду (3-й разряд встречается 7 раз, т.е. это наибольшая частота). | |||||||||||||||||||||||||||
| Номер медианы - | |||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
| , где n - число членов ряда. | |||||||||||||||||||||||||||||
| N Me = | 24 | + | 1 | = | 12,5 | ; | |||||||||||||||||||||||
| 2 | |||||||||||||||||||||||||||||
| Медиана - | |||||||||||||||||||||||||||||
| Ме = | 4 | -му разряду (так как номера 12 и 13 соответствуют 4-му разряду). | |||||||||||||||||||||||||||
| К показателям вариации относятся: |
| ||||||||||||||||||||||||||||
| среднее линейное отклонение | ( d ), | ||||||||||||||||||||||||||||
| среднее квадратическое отклонение | ( σ ), | ||||||||||||||||||||||||||||
| коэффициент вариации | ( V ). | ||||||||||||||||||||||||||||
| Для расчета показателей ряда распределения удобно использовать вспомогательную таблицу: | |||||||||||||||||||||||||||||
| Расчет показателей вариации | |||||||||||||||||||||||||||||
| Тарифный разряд, x | Число рабочих, f |
| ІdІ * f | d2 * f | |||||||||||||||||||||||||
| 2 | 3 | -1,9 | 5,8 | 11,02 | |||||||||||||||||||||||||
| 3 | 7 | -0,9 | 6,4 | 5,88 | |||||||||||||||||||||||||
| 4 | 6 | 0,1 | 0,5 | 0,04 | |||||||||||||||||||||||||
| 5 | 5 | 1,1 | 5,4 | 5,87 | |||||||||||||||||||||||||
| 6 | 3 | 2,1 | 6,3 | 13,02 | |||||||||||||||||||||||||
| Итого | 24 | — | 24,3 | 35,83 | |||||||||||||||||||||||||
|
|
| = | ∑│d│*f | = | 24,3 | = | 1,0 | разряда; | |||||||||||||||||||||
| ∑f | ∑f | 24 | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
| 35,83 | = | 1,22 | разряда; | ||||||||||||||||||||||||||
| 24 | |||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
| 1,22 | *100%= | 31,2% | |||||||||||||||||||||||||||
| 3,9 | |||||||||||||||||||||||||||||
| Следовательно, | |||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
| Как видно на рис. 4.1., распределение рабочих по тарифному разряду несимметрично, поэтому определяется показатель асимметрии: | |||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||
| 3,9 | - | 3 | = | 0,75 | . | ||||||||||||||||||||||||
| 1,22 | |||||||||||||||||||||||||||||
| Следовательно, | |||||||||||||||||||||||||||||
Задача для самостоятельной работы
| Задача 4.1 | |||||||||||||||||||||||
| По приведенным ниже данным о квалификации рабочих цеха требуется: | |||||||||||||||||||||||
| - построить дискретный ряд распределения; | |||||||||||||||||||||||
| - дать графическое изображение ряда; | |||||||||||||||||||||||
| - вычислить показатели центра распределения, показатели вариации и формы распределения. | |||||||||||||||||||||||
| Тарифные разряды 24 рабочих цеха: | |||||||||||||||||||||||
| 5 | 5 | 6 | 5 | 6 | 6 | 3 | 6 | 6 | 6 | 6 | 6 | 6 | 5 | 6 | 5 | 3 | 2 | 6 | 3 | 4 | 4 | 5 | 3 |
Дата добавления: 2018-05-12; просмотров: 622; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!