Что такое комплексный чертеж и каковы правила его применения.
Введение………………………………………………………………………………………………...2 1.1 Как образуются дополнительные форматы чертежей....................................................................2 1.2 Что называется сопряжением, уклоном и конусностью…...............................................................3 1.3 Что такое комплексный чертеж и каковы правила его применения…............................................5 1.4 На какие виды делятся аксономентрические проекции в зависимости от направления лучей....6 1.5 Какое изображение называется видом и сколько их может быть..................................................7 1.6 Что такое разрез, с какой целью он выполняется…........................................................................9 1.7 Как делятся разрезы в зависимости от числа секущих плоскостей, участвующих в разрезе....10 1.8 Какое изображение называется сечением, какое оно бывает.......................................................13 1.9 Что такое технический рисунок, и чем он отличается от художественного...............................16 1.10 Какие виды конструкторской документации установлены гостом ГОСТ 2.102. – 68…………17 1.11 Составьте таблицу: «Виды резьб»…………………………………………………………………19 1.12 Выполните таблицу: «Условные графические обозначения в кинематических схемах»...…...20 2. Список используемой литературы…………………………………..………………………………26
Введение
Инженерная графика - это наука создания проекционных изображений, которая состоит из двух частей: начертательной геометрии и технического черчения.
|
|
|
Как образуются дополнительные форматы чертежей.
Формат чертежа - это лист бумаги определенного размера. Существует государственный стандарт ГОСТ 2.301-68 в котором прописаны размеры форматов необходимых для использования при выполнении чертежей и других документов, используемых в конструкторской документации.
Форматы делятся на основные и дополнительные. К основным форматам относят формат с размерами сторон 1189 х 841 мм (площадь 1 м2) и другие форматы полученные путем последовательного деления предыдущего основного формата на две равные части - линией, параллельной меньше стороне предыдущего формата. Размеры сторон формата площадью 1м2 выбраны таким образом, чтобы при делении пополам большей стороны формата получится прямоугольник, подобный исходному. Дополнительные форматы образуются увеличением коротких сторон основных форматов на величину, кратную их размерам.
Обозначение основных форматов состоит из букв А и арабской цифры от 0 до 5. Обозначение дополнительных форматов состоит из обозначения основного формата и его кратности. Предельные отклонения сторон форматов - в пределах от 1,5 до 3 мм в зависимости от размера стороны. Размеры основных и дополнительных форматов приведены ниже в таблице.
|
|
|
Обозначения и размеры сторон основных и дополнительных форматов
по ГОСТ 2.301-68
| Основные форматы | Дополнительные форматы | ||
| Обозначение | Размеры сторон, мм | Обозначение | Размеры сторон, мм |
| А0 | 841 х 1189 | А0 х 2 А0 х 3 | 1189 х 1692 1189 х 2523 |
| А1 | 594 х 841 | А1 х 3 А1 х 4 | 841 х 1783 841 х 2378 |
| А2 | 420 х 594 | А2 х 3 А2 х 4 А2 х 5 | 594 х 1261 594 х 1682 594 х 2102 |
| А3 | 297 х 420 | А3 х 3 А3 х 4 А3 х 5 А3 х 6 А3 х 7 | 420 х 891 420 х 1189 420 х 1486 420 х 1783 420 х 2080 |
| А4 | 210 х 297 | А4 х 3 А4 х 4 А4 х 5 А4 х 6 А4 х 7 А4 х 8 А4 х 9 | 297 х 630 297 х 841 297 х 1051 297 х 1261 297 х 1471 297 х 1682 297 х 1892 |
| А5 | 148 х 210 | - | - |
| Примечание. Формат А5 допускается применять при необходимости. | |||
1.2 Что называется сопряжением, уклоном и конусностью.
В очертаниях различных геометрических форм часто встречаются плавные переходы от одной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, как правило, дуги окружности называется сопряжением.
Построение сопряжений основано на следующих положениях геометрии.
Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной t к окружности (рис. 1, а). Радиус окружности r, проведенный в точку касания К, перпендикулярен к касательной прямой.
|
|
|
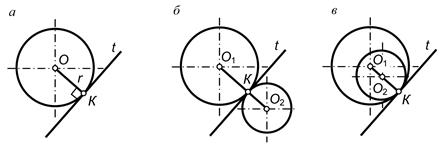Рис. 1
Переход от одной окружности к другой окружности в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную. Точка касания К и центры окружностей O1 и О2 лежат на одной прямой. Если центры окружностей лежат по разные стороны от касательной t, то касание называется внешним (рис. 16, б); если центры O1 и О2находятся по одну сторону от общей касательной — соответственно внутренним (рис. 1, в).
В теории сопряжений применяются следующие термины (рис. 2):
· центр сопряжения — точка О, равноудаленная от сопрягаемых линий;
· точки сопряжения К1и К2 — точки касания двух сопрягаемых линий;
· дуга сопряжения К1К2— это дуга окружности, с помощью которой выполняется сопряжение;
· радиус сопряжения R — это радиус дуги сопряжения.
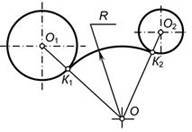Рис. 2
В общем случае построение сопряжения двух линий при заданном радиусе сопряжения состоит из следующих этапов:
1) построение множества точек, находящихся на расстоянии радиуса сопряжения от первой из сопрягаемых линий;
2) построение множества точек, находящихся на расстоянии радиуса сопряжения от второй из сопрягаемых линий;
|
|
|
3) определение на пересечении центра сопряжения;
4) определение точки сопряжения на первой из сопрягаемых линий;
5) определение точки сопряжения на второй из сопрягаемых линий;
6) проведение дуги сопряжения в интервале между точками сопряжения.
Уклон — это величина, характеризующая наклон одной прямой линии к другой прямой.
Уклон отрезка АВ задают отношением катетов прямоугольного треугольника АВС (рис. 3, а) или в процентах (рис. 3, б)
Если уклон задается в процентах, например, 15% (рис. 3, б), то длину одного из катетов принимают равной 100%, а другого - 15%. Уклон 15% есть уклон 1: 5. По ГОСТ 2.307- 68 перед размерным числом, определяющим уклон, наносят условный знак, острый угол которого направлен в сторону уклона.
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле С=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: С = (D-d)/h.
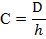
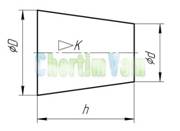
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
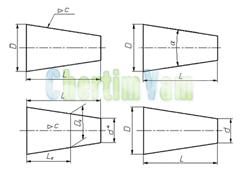
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах. Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25'16", десятичной дробью 0,2 и в процентах 20. Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы - 30, 45, 60, 75, 90 и 120°.
Что такое комплексный чертеж и каковы правила его применения.
Комплексным чертежом называется изображение предмета двумя или несколькими его ортогональными проекциями с сохранением проекционной связи.
Условие обратимости выполняется ортогональным проецированием объекта на две (П1, П2) или три (П1, П2, П3) взаимно перпендикулярные плоскости проекций (см. рисунок 5).
Плоскость П1 называют горизонтальной плоскостью проекций, П2 — фронтальной, П3 — профильной.
Прямые пересечения плоскостей проекций называют осями проекций X,Y,Zили координатными осями; цифрой О обозначена точка пересечения всех трех осей проекций (начало координат).
В 3-х мерном пространстве положение точки определяется с помощью прямоугольных координат X,Y,Z: X –абсцисса, Y -ордината, Z –аппликата.
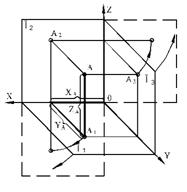Рисунок 5
Рассмотрим образование комплексного чертежа на примере простейшего элемента пространства — точки.
Для построения проекций точки А проведем через нее три проецирующие прямые, перпендикулярные соответствующим плоскостям проекций. Точки А1, А2, А3 пересечения проецирующих прямых с плоскостями проекций будут искомыми проекциями точки А.
Для получения плоского (комплексного) чертежа горизонтальная плоскость проекций П1 совмещается с фронтальной плоскостью проекций П2путем вращения вокруг оси Х. Профильная плоскость П3 совмещается с фронтальной плоскостью проекций П2 путем вращения вокруг оси Z. На рисунке показано направление вращения.
Комплексный чертеж точки представлен на рисунке 6.
Прямые линии, соединяющие проекции две точки и перпендикулярные осям проекций (X,Y,Z)называют линиями проекционной связи.
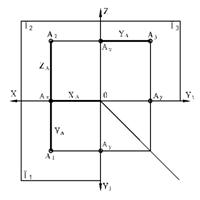Рисунок 6
Комплексный чертеж обладает следующими свойствами:
— две проекции точки определяют ее положение в пространстве;
— две проекции точки лежат на одной линии связи, перпендикулярной оси проекций;
— по двум проекциям точки можно построить третью;
— удаление точки от плоскости П1 определяет координата Z, от плоскости П2 — Y, от плоскости П3 — X.
Способом параллельного проецирования можно получить аксонометрические проекции.
Дата добавления: 2018-05-12; просмотров: 5944; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!