Кинематика входного звена. Свяжем системы координат XOY c точкой О.

Министерство образования Республики Беларусь

Министерство образования и науки Российской Федерации

 

Учреждение образования

БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ

Кафедра «Автоматизированные системы управления»

 

 

С.К. Крутолевич Н.М. Щербо

 

ЭКСПЕРТНЫЕ СИСТЕМЫ

 

 

Лабораторный практикум

 

для студентов специальности

"Автоматизированные системы обработки информации"

 

Могилев 2013

    Данный лабораторный практикум содержит 12 лабораторных работ, выполнение которых закрепляет материал, изложенный в электронном конспекте лекций по дисциплине «Экспертные системы» С.К. Крутолевич, Н.М. Щербо, Могилев 2013.

 Для выполнения лабораторных работ необходимо получить у преподавателя файл “№варианта”.xls с индивидуальной базой исходных данных.

 

 

Лабораторная работа №1 Проведение математического моделирования.

Случайные события. Определение вероятности.

 

Цель Разработка программного обеспечения  для моделирования процесса возникновения случайных событий

 

Теоретический материал

 

Теория вероятностей рассматривает не все случайные эксперименты, а только те, которые имеют свойство статистической устойчивости. Прежде чем объяснить это свойство, введем некоторые основные понятия.

Случайный эксперимент определяется совокупностью условий, в которых он проводится, и совокупностью всех возможных результатов. Проведение случайного эксперимента предполагает выполнение определенного комплекса условий. Случайный эксперимент, т. е. проведение опыта и получение соответствующего результата, называют еще испытанием.

Считается, что часть условий, определяющих случайный эксперимент, остается постоянной по объективным и субъективным причинам. Наряду с постоянными условиями на результаты случайного эксперимента оказывает влияние также и ряд объективных факторов, поведение которых не известно или известно частично. Постоянные условия определяют именно то среднее, о котором можно говорить уверенно, то, что устанавливается закономерно в случайных явлениях. Постоянные условия дают возможность повторения случайного эксперимента произвольное число раз, при этом выявляется средняя закономерная тенденция. Переменные факторы (условия) определяют случайное, непредсказуемое в случайном эксперименте. Отсюда, говоря о повторении опыта при одинаковых условиях, нужно иметь в виду, что неизменными остаются условия только первой группы — постоянные.

При обработке некоторой детали на станке можно поддерживать постоянными скорость и глубину резания, подачу, марку материала и т. д. Однако однородность материала, первоначальные размеры заготовки, вибрации станка и т. д. изменяются в определенных не всегда известных нам пределах. Поэтому при подобном опыте возможны различные конечные результаты, которые нельзя предсказать до его проведения. Благодаря постоянным условиям опыта можно определить в среднем, какая часть продукции будет годной, а какая нет. Однако из-за переменных факторов до обработки данной детали нельзя сказать будет она годной или нет.

Любой факт (исход, результат), который может появиться или не появиться при проведении опыта, называется в теории вероятностей случайным событием. Например, в рассмотренном эксперименте возможны следующие исходы: обработанная деталь окажется годной или негодной. Это два случайных события, каждое из которых может наступить или не наступить в результате проведенного опыта. Случайное событие чаще всего обозначают прописными латинскими буквами А, В, С, D и т. д.

В качестве случайного события можно рассматривать работоспособность дискеты, время до отказа вычислительной техники.

Теперь объясним понятие статистическая устойчивость. Это необходимое свойство изучаемых в теории вероятностей случайных экспериментов. Пусть А одно из возможных событий данного случайного эксперимента, этот эксперимент повторен n раз и при этом событие А появилось m раз.

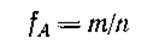
(1.1)

Величина f_A называется относительной частотой появления события А. Если повторить несколько раз серию, состоящую из n одинаковых опытов, то в общем случае величина f_A не будет постоянной. Ее численные значения будут различными также и при разных значениях n. Свойство устойчивости в данном случае состоит в том, что при большом n относительная частота f_A начинает слабо колебаться около некоторого постоянного числа.

При многократном наблюдении за одним или несколькими случайными экспериментами можно заметить, что некоторые события появляются чаще, а другие реже. Это значит, что одни имеют большую возможность появления, а другие меньшую. Например, если многократно подбрасывать две игральные кости и подсчитывать сумму появляющихся очков, то можно заметить, что некоторые суммы, например 6, 7, 8, появляются чаще, а другие, например 2, 3, 11, 12 — реже.

Мерой объективной возможности появления данного случайного события А является его вероятность Р(А). Вероятность появления данного события —• объективная величина, которая существует независимо от экспериментатора. Она определяется полной совокупностью условий, при которых может появиться данное событие. Сказанное здесь математически не объясняет понятия вероятность, так как оно не определяет ее количественно. Исчерпывающей математической формулировки этого понятия все еще не существует. Важное значение для теории и практики имеют приведенные дальше определения этого фундаментального понятия.

В основе классического определения вероятности лежит одно элементарное понятие о равновозможных событиях, которое не подлежит определению. Если в данном случайном эксперименте имеем равновозможные события, то при его многократном повторении можно ожидать, что эти события появятся равное число раз. Типичные примеры равновозможных событий дает подбрасывание игральной кости или монеты.

Если возможные события некоторого случайного эксперимента не могут быть разложены на более простые, то их называют элементарными событиями этого эксперимента. Классическое определение вероятности связано с тем случаем, когда все элементарные события являются равновозможными и при любом опыте появляется только одно из них.

Пусть интересующий нас случайный эксперимент имеет n равновозможных элементарных событий и пусть при появлении m из них наступает и событие А. Тогда можно сказать, что из всех n возможных элементарных событий m благоприятствуют появлению события А. При этом вероятность Р(А) будет равна отношению числа элементарных событий, которые благоприятствуют событию A, к числу всех возможных элементарных событий:

 

Р(А)=m/n

 

Это так называемое классическое определение понятия вероятности.

 

Пример  В коробке, состоящей из десяти дискет, есть три негодные. Определить вероятность того, что из четырех случайно отобранных две окажутся негодными.

Решение. Число всех возможных способов выбрать четыре дискеты из десяти равно числу сочетаний С⁴₁₀, образованных из десяти элементов по четыре. Тогда число всех возможных

элементарных событий Сkn=n!/(k!(n-k)!)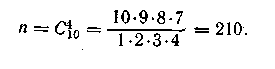

Число элементарных событий, которые благоприятствуют событию А, т. е. взятию четырех дискет, две из которых будут негодными, определим так: две негодные дискеты можем взять из трех негодных С²₃ = 3 различными способами. Оставшиеся, две дискеты из четырех должны быть годными, их можно взять из 10 — 3=7 годных дискет С²₇ = 21 различными способами. Этот 21 способ можно сочетать с любым из трех способов взятия двух из трех негодных дискет, т. е. число элементарных событий, которые благоприятствуют событию А, будет m= 3*21 = 63. Тогда искомая вероятность

 

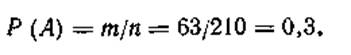
Практическое задание

 

Разработать программное обеспечение, для вычислительного эксперимента.

В коробке, состоящей из n дискет,  k—негодные. Определить вероятность события А, что из d случайно отобранных b окажутся негодными.

Числовые значения переменных k, d и b в индивидуальном задании.

Реализованный пример на листе “Lr1” файла MISPR_Т1.xls.

В модуле1 данного файла  находится программа генерации случайных событий «LR1» и программа определения частоты появления случайного события «Частота».

Порядок выполнения работы:

1. Определить вероятность события А, используя формулы сочетаний.

2. Разработать алгоритм и программу для моделирования данного эксперимента со своими исходными данными.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы моделирующей данный эксперимент.

3.1.2. Представить график частоты появления события А от числа опытов.

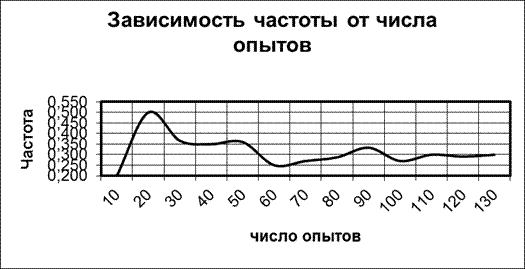
3.1.3. В заключении указать при каком числе опытов выполняется условие, что  |f_A-P(A)|<№вар/100

 

4. Ответить на контрольные вопросы

4.1 Дать определение «относительной частоте появления событий»

4.2 Дать определение «вероятности появления событий»

4.3 Определить вероятность достоверного и невозможного события.

 

 

Лабораторная работа №2

Разработка системы автоматизированного проектирования для кинематического анализа и синтеза рычажного механизма.

 

Цель: Разработка программного обеспечения СППР на основе имитационного моделирования рычажных механизмов.

 

Теоретический материал.

 

Целью кинематического анализа является определение координат точек рычажного механизма. Необходимо, задавая положение входного звена ОА через угол 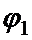определить координаты центров кинематических пар.

Кинематический анализ начинается с входного звена, продолжается с первой присоединенной структурной группы и завершается анализом второй присоединенной структурной группы.

Перед началом геометрического анализа механизмов вспомним некоторые формулы, для решения треугольника.

Прямоугольный треугольник. АВС, С=π/2.

АС=АВ*cos(A), BC=АВ*sin(A), BC=AC*tg(A).

Произвольный треугольник АВС

	A+B+C=p
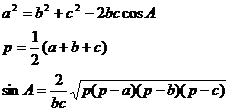
Рис. 1 Решение треугольника

 

Кинематика входного звена. Свяжем системы координат XOY c точкой О.

	Входное звено ОА образует с системой координат прямоугольный треугольник ОАК. При этом известна длина звена ОА и входной угол 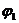. Координаты точки А определяются по формулам. ;
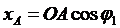Рис. 2 Решение входного звена.

 

Структурная группа первого вида. Перед решением структурной группы первого вида должны быть известны координаты внешних точек А и С. Цель решения найти координаты точки В.

	1 Определим расстояние АС 2 Определим угол между осью Х и лучом СА. 3 Определим угол С треугольника АСВ, угол φ3 между осью Х и лучом СВ и координаты точки В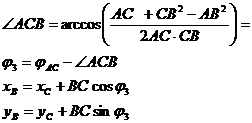
Рис. 3 Решение структурной группы первого вида

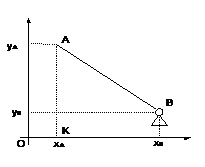
Структурная группа второго вида.

 Для облегчения вывода удобно совместить одну из осей координат с направляющей.

Известны координаты внешней точки А и положение направляющей, вдоль которой перемещается точка В. Данная направляющая задает одну из координат точки В. Необходимо определить вторую координату точки B.

	В прямоугольном треугольнике АВK определяется угол А. Затем расстояние КВ и координату х точки В. В данном случае Yb=0
Рис. 4 Решение структурной группы второго вида

 

Структурная группа третьего вида.

В данной группе координаты внешней вращательной кинематической пары А и внутренней поступательной кинематической пары А’ совпадают. Поэтому их отмечают одной буквой. Координаты второй внешней вращательной пары О₁ также заданы. Требуется найти угол между звеном О₁А и координатной осью 0Х.

.

 

	Из треугольника АВK определяется величина угла АВК. Искомый угол φ3 дополняет АВК по величины π
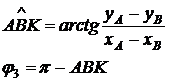
Рис. 5 Решение структурной группы третьего вида

 

 

Структурная группа пятого вида.

В данной группе координаты внешней вращательной кинематической пары А и внутренней поступательной кинематической пары А’ совпадают. Поэтому их отмечают одной буквой. Одна из координат второй внешней поступательной пары С также задана. Требуется найти вторую координату точки С.

	Вторая координата точки С совпадает с координатой точки А. YC=const, XC=XA
Рис. 6 Решение структурной группы пятого вида

 

Порядок выполнения работы:

1. В соответствии с заданной схемой механизма необходимо составить математическую модель определения координат: центров кинематических пар от угла поворота φ входного звена от оси ОХ.

2. Разработать алгоритм и программу для моделирования данного эксперимента со своими исходными данными. Угол φ изменяется от 0 до 2π. При этом механизм совершает один цикл движения.

Вариант механизма выбирается из приложения 1 в конце лабораторного практикума.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить математическую модель моделирующей данный эксперимент.

3.1.2. Представить блок схему программы

3.1.3. Привести распечатки различных положений механизма.

4. Ответить на контрольные вопросы

4.1 Дать определение «кинематическая пара»

4.2 Дать определение «число степеней свободы»

 

Работа № 3 Множества и события

    Цель Разработка программного обеспечения для определения относительной частоты появления случайного события, используя математический аппарат теории множеств.

 

Теоретический материал

Отдельные элементарные события данного случайного эксперимента можно рассматривать как элементы некоторого множества. Тогда совокупность всех возможных исходов данного эксперимента будет представлять собой множество I элементарных исходов. Это множество в теории вероятностей называется также пространством, (множеством) элементарных событий.

Обычно представляет интерес какая-либо комбинация элементарных событий, называемая случайным событием. Например, при подбрасывании игральной кости пространство элементарных событий имеет шесть элементов: 1, 2, 3, 4, 5, 6. Случайное событие — появление четного числа точек будет комбинацией только трех элементов: 2, 4 и 6 указанного пространства. Всякое случайное событие можно рассматривать как подмножество (подпространство). Отдельные элементарные события можно рассматривать как элементарные подмножества.

Если отдельные элементарные события равновозможны и число элементов в пространстве I конечно, то вероятность события А можно определить как отношение числа элементов подпространства А к числу элементов пространства I, т. е.

 

Р(А) = m(А)/n(I).     3.1

 

Пространства I и Ф также можно рассматривать как события, вероятности которых согласно формуле (1.15) будут

(3.2)

 

Следовательно, пространство I элементарного события и его пустое подпространство Ф являются достоверным и невозможным событием соответственно.

Если А случайное событие, то 0 < m(A) < m(I) и согласно формуле (3.1)

 0 < Р(А) < 1. Это соответствует классическому определению вероятности.

Если элементарные события пространства I не являются равновозможными, то изложенное здесь остается в силе, но необходимо отдельные элементарные события брать с соответствующим весом. Веса можно брать пропорциональными относительной частоте соответствующего элементарного события. Сумма всех весов должна быть равна единице.

Событие, состоящее в появлении хотя бы одного из событий А и В в данном опыте, называется суммой событий A и В и обозначается С₁ = A + В (читается так: С₁ равно A или В). Появление события С₁ означает появление A или В, или A и В вместе. Событие С₁ {2, 4, 5, 6} в примере 1.4 будет суммой A {2, 4, 6} и В {4, 5, 6}.

Событие, состоящее в появлении обоих событий A и В в данном опыте, называется произведением событий A и В и обозначается С ₂ = AВ (читается так: С₂ равно A и В).

Событие С₂ {4, 6 } является произведением событий A и В, соответствующих множествам A и В в примере 1.4.

События А и ‾А, для которых выполнены равенства A+‾А =I и A‾А = Ф, называются противоположными. Первое равенство показывает, что в любом опыте будет появляться одно из противоположных событий, второе — что в одном и том же опыте они появиться одновременно не могут.

Два события А и В называются несовместимыми, если их появление в одном и том же опыте невозможно, т. е. если АВ = Ф. Если эти события могут появиться в одном опыте, то они совместимы. Например, события А {2, 4, 6} и В {4, 5, 6} примера 1.4 совместимы, так как появление очков 4 и 6 означает появление A и Б.

 

Теоремы сложения и умножения вероятностей

 

Пусть имеются два несовместимых события A и  В, каждое из которых может осуществиться в m(А) и m(В) элементарных событиях. Если разделить обе части равенства на общее число элементарных событий, то получим

 

 

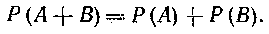
Равенство ( ) выражает сущность так называемой теоремы сложения вероятностей несовместимых событий.

Аналогично из равенства (1.13) можем получить равенство

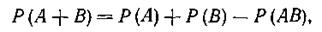
которое выражает сущность теоремы сложения вероятностей совместимых событий.

Если полная группа событий состоит только из двух противоположных событий A и ‾А, то равенство ( ) принимает вид

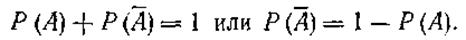
Если вероятность данного события В не зависит от появления или не появления другого события А, т. е.

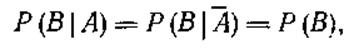
то будем считать, что событие В независимо от события А. В противоположном случае событие В зависимо от А. Свойство независимости событий взаимно, т. е. если Р (В|А ) = Р (В), то и Р (А|B) =Р(А).

Определить условную вероятность данного события, исходя из классического определения, нетрудно.

Пусть данный случайный эксперимент имеет n равновозможных элементарных событий и пусть А и В представляют собой какие-либо комбинации этих событий. На основе событий А и В можем образовать полную группу несовместимых событий: АВ, А‾В, ‾АВ и ‾А‾В.

 Пусть каждому из этих событий благоприятствует соответственно элементарные события n₁, n₂, n₃, и n₄.  Тогда их вероятности будут

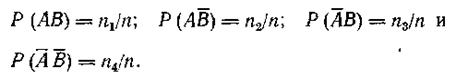
Для выполнения условия 1.26 необходимо, чтобы

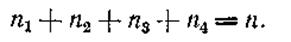
Так как событие А появляется только при появлении событий АВ и А‾В, то ему будут благоприятны n₁ + n₂ из всех n. Аналогично событию В будут благоприятны n₁ + n₃. Тогда можем записать:

При условии, что событие A появилось, n₁ + n₂ элементарных событий, которые были благоприятны событию A, образуют множество равновозможных элементарных событий, при появлении одного из которых возможно появление события В. При этом число элементарных событий, благоприятных событию В, уже будет n₁. Тогда можно записать

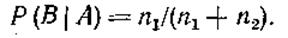
Сравнивая Р(АВ) из (1.30) с Р(А) из (1.31) и Р (В|А) из(1.32), получаем

Аналогично получаем равенство

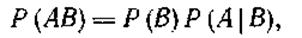
т. е. вероятность произведения двух совместимых событий равна произведению вероятности одного события, независимо какого, и условной вероятности другого.

Из формулы (1.33) можем определить, если Р (А) <> 0, условную вероятность

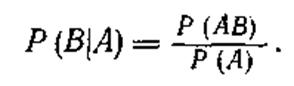
Если Р (А) = 0, то условная вероятность становится неопределенной.

В этих выражениях все условные вероятности заменяются безусловными.

 

Формула полной вероятности

Пусть имеется полная группа попарно несовместимых событий А₁, А ₂, ., А_n и событие В может появляться совместно с любым из событий этой группы. Пусть известны вероятности Р (A_i) и Р (B|Ai), где i = 1,2, . . ., п. Определим безусловную вероятность Р (В) события В. Для определения этой вероятности рассмотрим группу событий:

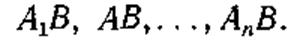
Эти события являются несовместимыми, но не образуют полной группы, так как в данном опыте может не появиться ни одно из них, а появится событие А_i‾_:В (i = 1, 2, ., n).

Отсюда ясно видно, что появление события В означает появление любого из несовместимых событий, т. е.

Тогда, используя теорему сложения вероятностей, получим

Если для каждого слагаемого в правой части (1.40) используем теорему умножения вероятностей, то для Р (В) получим

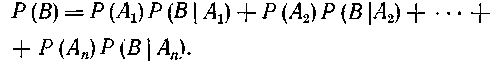
Эта формула называется формулой полной вероятности.

В ряде случаев в теории и практике представляет интерес определение вероятности события A_i (i = 1, 2, . . ., n) при условии, что в опыте появилось событие В, т. е. определение условной вероятности Р (А_i|В). Вероятность Р (А_i|В). называют апостериорной (послеопытной).

Согласно теореме умножения вероятностей можно записать

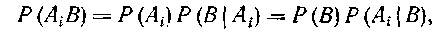
откуда

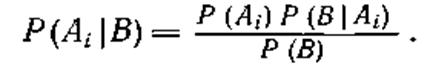
Эта известная формула Байеса находит применение в различных областях.

 

Пример 1 В партии, состоящей из 20 изделий, имеется три негодных. Из партии взяты наугад последовательно два изделия без возвращения.

Определить вероятность Р (А) того, что первое изделие будет негодным. Определить безусловную вероятность Р (В) того, что второе изделие будет негодным.

Решение. Пользуясь классическим определением вероятности, получим Р (А) = 3/20.

Событие В (второе изделие негодное) может наступить с любым из противоположных событий А и ‾А, которые образуют полную группу несовместимых событий, т. е. для Р (В) может быть применена формула полной вероятности.

Имея в виду, что Р (А) = 3/20; Р (‾А) = 17/20; Р (В|А) = 2/19; Р (В| ‾А) =3/19 и получаем

Отсюда, безусловная вероятность взятия негодного изделия при условии, что взятое перед ним изделие не возвращается, остается постоянной.

Пример 2. Блоки питания изготовляются на трех различных предприятиях: на первом изготовляется 20, на втором — 30 и на третьем — 50% . Первое предприятие гарантирует, что 90% деталей будут работать безотказно не менее 1000 ч, второе, что 95% деталей и третье, что 97%. До истечения 1000 ч работы блок питания выходит из строя. Определить вероятность изготовления этой детали каждым из предприятий.

Решение. ОбозначимА₁, А₂, и А₃ события того, что один случайно выбранный блок изготовлен соответственно на первом, втором и третьем предприятиях.

Вероятность того, что случайно выбранный блок выйдет из строя до истечения 1000 ч, согласно условию задачи будет

 

Искомыми вероятностями будут Р (А₁|В), Р (A₂|B) и Р(А₃|В). События A₁, A₂ и А₃ образуют полную группу несовместимых событий, а событие В может появиться только совместно с некоторым из них, т. е. условия использования формул полной вероятности и Байеса выполнены. Тогда согласно (1.42)

Видно, что вероятность события (гипотезы) A₁ до опыта была Р (A₁) = 0,2, а после опыта, когда уже известно, что событие В наступило, вероятность этой гипотезы уже Р (А₁|В) = 0,4. Таким образом, формула Байеса дает возможность после опыта сделать переоценку вероятности рассматриваемых гипотез.

 

 

Практическое задание

Используя в качестве источника данных интернет (например onliner.by) составить базу данных из выбранной предметной области (Приложение Б).

Индивидуальная БД представляет собой таблицу в 30  строк. В качестве столбцов выступают показатели качества и цена. Не менее 6 параметров качества. Обязательно включить параметр «Остаточная стоимость через 2-3 года»

 

Пример БД «Велосипеды»

	База фактов в реальных величинах
№	Модель	Число передач	Высота подъема руля	Диаметр колес	Вес, кг	Остаточная стоимость через 2-3 года	Цена, RR
	Номер параметра качества	1	2	3	4	5	6
1	Schwinn Sierra	7,00	80,00	26,00	13,6	0,50	29350
2	Orbera Carpe H40	24,00	75,00	28,00	13,0	0,50	19400
3	Giant Escape 2	3,00	80,00	28,00	14,5	0,70	22375
4	Merida Speeder T3	27,00	90,00	26,00	13,2	0,70	25188
5	Orbera Dude A10	1,00	50,00	26,00	10,2	0,60	37526

 

  Введем обозначение следующих элементарных событий:

А1-первый параметр в диапазоне 0..1/4 от размаха параметра.

А2- первый параметр в диапазоне 1/4…2/4 от размаха параметра.

А3- первый параметр в диапазоне 2/4…3/4 от размаха параметра.

А4- первый параметр в диапазоне 3/4. . 1 от размаха параметра.

Аналогично события B1, B2, B3,B4 – для второго параметра, С1, C2 C3 C4 – для третьего; D1, D2, D3, D4 для третьего; F1, F2, F3,F4 для четвертого; J1…J4-для пятого и H1..H4 для шестого параметра

Считая все события равновероятными, используя свойства множеств определить вероятность появления события G, выраженного через события G=f(Ai,Bi,Ci,Di,Fi,Ji).

 Уравнение события G представлено в приложении

 

Порядок выполнения

1. Разработать программу для определения количества элементов в соответствующем множестве и определить вероятности появления всех элементарных событий.

2. Определить вероятность события G, используя теоремы сложения и умножения вероятностей.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2. Представить вероятности элементарных событий.

3.1.3. Представить формулу и результаты определения вероятности события G.

4. Ответить на контрольные вопросы

4.1 Дать определения «пересечения и дополнения множеств»

4.2 Дать определения «коммутативного, ассоциативного и дистрибутивного законов»

4.3. Дать определение теоремы сложения вероятностей несовместимых событий.

4.4. Дать определение теоремы сложения вероятностей совместимых событий.

4.5. Дать определение условной вероятности и формулы Байеса. Определить вероятность нахождения показателей качества на заданном уровне при определенном целевом уровне.

 

Работа №4 Числовые характеристики случайных величин

Цель Разработка программного обеспечения для определения статистических характеристик случайной величины.

 

Теоретический материал

 

Часто при изучении явления или процесса не нужно знать подробно случайные величины, которые его описывают, т. е. знать законы распределения этих величин, а вполне достаточно знать некоторые их особые численные значения и характеристики. Такими характеристиками являются моменты, квантили и числовые характеристики. При этом одни числовые характеристики полностью совпадают с некоторыми моментами, а другие являются их функциями.

Понятие «момент» широко используется в механике для описания распределения масс и площадей (статические моменты, моменты инерции и т. д.). Аналогичным образом это понятие используют в теории вероятностей для описания распределения значений случайной величины. При этом в теории вероятностей чаще всего используют начальные и центральные моменты и реже абсолютные. Для всех видов моментов существует так называемый порядок соответствующего момента.

Начальный момент k-го порядка случайной величины X обозначается m_k [X]. Для дискретных случайных величин его определяют по формуле

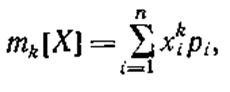
где n—число возможных значений X; x_i;— i-е значение X; р_i — вероятность, с которой X принимает численное значение x_i.

В теории и практике чаще всего используют первый начальный момент m₁[X ]. Если из X вычесть m₁ [X ], то получим так называемую центрированную случайную величину

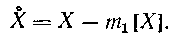
Начальные моменты центрированной случайной величины X называют центральными моментами нецентрированной случайной величины X, обозначают μ_k[X] и для дискретных случайных величин

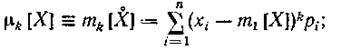
Из центральных моментов чаще всего используют второй μ₂ [X], который совпадает с так называемой дисперсией σ²[X] случайной величины X. Первый центральный момент всех случайных величин равен нулю, т. е. μ₁ [X]=0.

Числовые характеристики случайной величины делятся на следующие группы:

1) определяющие положение случайной величины;

2) определяющие рассеивание случайной величины;

3) связанные с симметрией и степенью заострения кривой распределения случайной величины.

К первой группе характеристик относятся: среднее значение, мода и медиана. Из этих характеристик самую важную роль в теории вероятностей играет среднее значение m₁[X], которое называют также математическим ожиданием. Математическое ожидание данной случайной величины совпадает с ее первым начальным моментом, который вычисляют по формуле (2.10) или (2.11), если положить k = 1.

Математическое ожидание является центром, около которого группируются в той или другой степени возможные значения данной случайной величины.

Модой М случайной величины X называют ее численное значение, которому соответствует самая большая вероятность для дискретных случайных величин и максимум плотности распределения f(x) — для непрерывных.

Если плотность распределения f(x) имеет только одну моду (один максимум), распределение называют одномодальным. В дальнейшем будем рассматривать только одномодальные распределения.

 

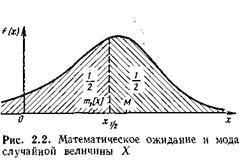
Медианой называют численное значение x_1/2 случайной величины, для которого выполнено условие

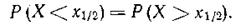
Для непрерывных случайных величин медиана равна абсциссе точки, ордината которой делит площадь под кривой распределения на две равные части.

Если для дискретных случайных величин нельзя найти численное значение, которое удовлетворяет условию, то определяют такие соседние значения х_k, и x_k+1, для которых выполняются неравенства

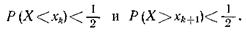
Тогда медианой будет среднее арифметическое этих двух соседних значений: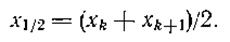

Если распределение симметрично относительно m₁[X], то медиана и математическое ожидание совпадают. Если при этом распределение одномодальное и x_1/2, совпадает с М и m₁[X] то мы имеем дело с широко используемым в теории и практике нормальным распределением.

Ко второй группе числовых характеристик случайной величины относятся: размах, дисперсия, среднее квадратичное отклонение и коэффициент вариации. Реже используется так называемое среднее арифметическое отклонение.

Размах R равен разности между самым большим и самым малым значениями X, т. е.

 

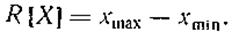
Дисперсия σ²[X] данной случайной величины равна математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания:

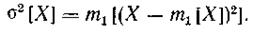
Дисперсия является основной характеристикой рассеивания Данной случайной величины относительно математического ожидания. Само название «дисперсия» означает «рассеивание». Из формулы (2.16) видно, что дисперсия совпадает со вторым центральным моментом М₂ [X].

Для дискретных случайных величин

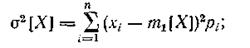
Дисперсию можно представить через первый и второй начальные моменты:

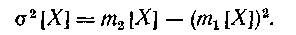
Так как дисперсия представляет собой сумму положительных слагаемых, которые являются квадратами отклонений случайной величины от математического ожидания, то малая дисперсия будет показывать, что эти слагаемые.(отклонения) малы и, следовательно, мало рассеивание. Наоборот, большая дисперсия показывает, что по крайней мере одно из отклонений велико и, следовательно, рассеивание большое. Это показывает, что, действительно, дисперсия может служить мерой степени рассеивания. Однако при использовании дисперсии имеется одно неудобство — ее размерность равна квадрату размерности изучаемой случайной величины, поэтому более удобной характеристикой рассеивания считается так называемое среднее квадратичное отклонение σ[X], которое определяют по формуле

При сравнении степени рассеивания двух случайных величин Х1 и Х2 необходимо иметь в виду также их математические ожидания m1[Х1] и m2[Х2]. Если они равны между собой, то сравнение можно проводить по σ² [Х1] и σ² [Х2] или по соответствующим средним квадратичным отклонениям. Если m1[Х1] не равно m2[Х2], то приходится использовать так называемый коэффициент вариации V [X], который определяют по формуле (в %)

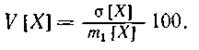
Коэффициент вариации является относительной мерой рассеивания. Характеристики рассеивания σ[X] и V [X] являются основными критериями для оценки качества и надежности работы различных технических устройств.

 

К третьей группе числовых характеристик относятся асимметрия и эксцесс. Значения некоторой случайной величины X могут быть распределены симметрично или асимметрично относительно математического ожидания m₁ [X]. Степень асимметрии (несимметрии) данного распределения характеризуют коэффициентом асимметрии γ₁[X], который вычисляют как отношение третьего центрального момента μ₃ [X] к σ[X], возведенному в третью степень:

Использование μ₃ [X] для определения степени асимметрии основывается на следующем. Как мы уже видели, первый центральный момент μ₁[X] всегда равен нулю. Это делает первый и все четные центральные моменты негодными для характеристики степени асимметрии. Нечетные центральные моменты третьего и более высокого порядков равны нулю только при симметричных распределениях. Так как с увеличением порядка центрального момента возрастает сложность его вычисления, логично при определении степени асимметрии использовать самый простой из них, т. е. третий центральный момент.

При γ₁ > 0 говорим о положительной (левой) асимметрии, а при γ₁ < 0 — об отрицательной (правой) асимметрии.

Эксцесс γ₂ [X] данного распределения характеризует степень его заостренности и вычисляется по формуле

 

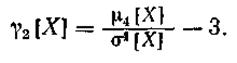
Основой для определения степени заостренности данного распределения является нормальное распределение при одной и той же дисперсии обоих распределений, При нормальном распределении. отношение четвертого центрального момента к σ⁴ [X] равно трем. Таким образом, эксцесс нормального распределения равен нулю.

Из всех рассмотренных до сих пор числовых характеристик самое большое приложение при исследовании и испытании имеют математическое ожидание, дисперсия, среднее квадратичное отклонение и коэффициент вариации.   Значительную информацию о распределении случайной величины дают и ее квантили. Квантили задают вероятность попадания случайной величины в интервал. Например α-квантиль х_α определяется из условия

 

 

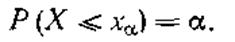
Практическое задание

Разработать программное обеспечение для определения статистических характеристик распределения параметров качества объектов предметной области (лабораторная работа 3).

 

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2 Представить значения

- оценки математического ожидания с помощью среднего значения,

- оценки математического ожидания с помощью медианы,

- оценки математического ожидания с помощью моды,

-оценки дисперсии и среднего квадратичного отклонения,

- оценки коэффициента вариации,

- оценки асимметрии и эксцесса.

 

4. Ответить на контрольные вопросы

4.1. Дать определение дискретной и непрерывной случайной величины и указать способы их задания.

4.2. Дать определение начального момента k-го порядка случайной величины.

4.3 Указать числовые характеристики определяющие положение случайной величины

4.4 Указать числовые характеристики определяющие рассеивание случайной величины

4.5 Указать числовые характеристики связанные с симметрией и степенью заострения кривой распределения случайной величины.

4.6 Дать определение репрезентативной выборке.

4.7 Дать определения несмещенной и состоятельной оценки характеристик случайной величины.

4.8 Сравнить эффективность оценки математического ожидания с помощью среднего значения и медианы.

 

 

Работа № 5 Законы распределения случайной величины

 

Цель Разработка программного обеспечения для определения статистических законов распределения характеристик случайной величины

 

Теоретический материал

 

Любая случайная величина полностью определяется законом распределения, который имеет две формы.

Для дискретных случайных величин — это ряд распределения и функция распределения, а для непрерывных — функция распределения и плотность распределения.

Ряд распределения содержит все возможные значения дискретной случайной величины и соответствующие им вероятности.

Функция распределения F(х) выражает вероятность Р того, что случайная величина X принимает значение меньшее данного действительного числа х, т. е.

 и имеет следующие свойства:

1) численные значения F (х) принадлежат интервалу [0, 1 ]:

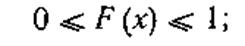
2) функция F(х) неубывающая, т. е. если x2 > х1 то F(х2) > F(x1)>;

3) если возможные значения случайной величины X принадлежат интервалу [а, b], то F(х) = 0 при х <= а и F(х) = 1 при х >= b.

Первое свойство связано с самим определением функции распределения как вероятности.

Второе свойство доказывается, если используются несовместимые события: случайная величина X принимает значение меньше х1 и случайная величина X принимает значение больше или равное. х1 и меньше х2.

Тогда событие: «случайная величина X принимает значение меньше х2” является суммой двух написанных выше несовместимых событий, поэтому можем записать равенство

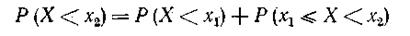
или

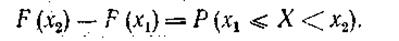
Видно, что вероятность того, что случайная величина X попадает в интервал (х1, х2), равна приращению функции распределения в этом интервале. Из этого равенства следует также, что вероятность того, что непрерывная случайная величина примет определенное численное значение, равна нулю. В этом. легко, убедиться, если подставить х2= х1, при этом получим

 

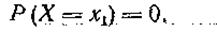Отсюда

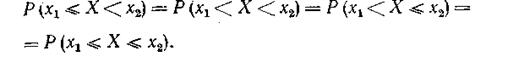
Из Р(X=x1) = 0 не следует, что событие X = х1 невозможно, т. е. что случайная величина X не может принимать численное значение x1, которое является одним из ее возможных численных значений.

Третье свойство функции распределения становится очевидным из-за того, что событие X < x1 <a невозможно, т. е. F(х1) = 0, а событие X < х2 >= b  является достоверным (так как возможные значения X меньше х2 ),т. е. F(х2) = 1.

Если возможные значения непрерывной случайной величины X принадлежат интервалу (-∞, +∞), третье свойство принимает вид

 

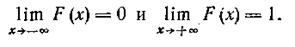
Рассмотренные свойства дают возможность получить представление о характере графика функции распределения. Например, из первого свойства следует, что этот график расположен между осью абсцисс (у = 0) и параллельной ей прямой с уравнением у = 1. Для дискретных случайных величин график функции распределения имеет ступенчатый характер, для непрерывных — монотонно неубывающий.

Плотность распределения f(x) — вторая форма закона распределения непрерывных случайных величин является первой производной функции распределения

Поэтому f(х) называется еще дифференциальной функцией. Если известна f(х), то согласно формуле Ньютона—Лейбница

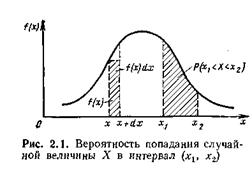
т. е. вероятность попадания непрерывной случайной величины X в интервал (х1, х2) равна значению определенного интеграла от плотности распределения f(х), вычисленному в пределах от х1 до х2. Геометрически это означает, что вероятность попадания X в интервал (х1, х2) равна площади криволинейной трапеции, ограниченной сверху графиком плотности распределения f(х), снизу осью абсцисс х, а с боков вертикальными прямыми х = х1 и х = х2 (рис. 2.1).

	Если подставим 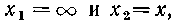то получим

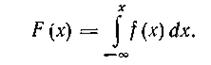
Отсюда вытекает второе название функции F(х)— интегральная функция.

При достаточно малом dх вероятность попадания непрерывной случайной величины X в интервал (х, х + dх) приблизительно равна площади прямоугольника с основанием dх и высотой f(х) (см. рис. 2.1).

Величина f(х) их называется элементарной вероятностью. Так как вероятность — безразмерная величина, то размерность плотности распределения f(х) обратна размерности случайной величины X.

Плотность распределения f(х) имеет следующие свойства:

1) она неотрицательна, т. е. f(х) > 0;

2) несобственный интеграл от f(х) в пределах от -∞до +∞ равен единице, т. е.

Если возможные значения X принадлежат интервалу (а, Ь), то (2.8) принимает вид

Таким образом, видно, что полная площадь, ограниченная графиком f(х) и осью абсцисс, равна единице.

Принято график плотности распределения f(х) называть кривой распределения.

Нормальный закон распределения, известный так же как закон Гаусса, находит широкое применение в различных областях познания. Он играет исключительно важную роль в теории вероятностей, теории ошибок, математической статистике и т. д. Именно для случая нормального распределения разработаны наиболее полно различные статистические методы.

Чрезвычайно широкое приложение нормального закона основывается на центральной предельной теореме. Согласно этой теореме, если имеем n независимых случайных величин Х1, Х2, . . ., Хn с конечными математическими ожиданиями и дисперсиями, то при n -›∞ закон распределения суммы или среднеарифметического значения данных случайных величин неограниченно стремится к нормальному, независимо от их закона распределения, достаточно только, чтобы между случайными величинами Х1, Х2, . . ., Хn не было доминирующих относительно влияния на сумму.

На практике считается, что распределение суммы 10—20 одинаково распределенных случайных величин достаточно близко к нормальному закону. В частном случае, когда случайные величины распределены по закону равной вероятности в интервале [0, 1], даже при n = 6 получается приемлемое приближение к нормальному закону.

Главной особенностью нормального закона является то, что это предельный закон, к которому стремятся остальные законы распределения при определенных условиях. Нормальный закон можно использовать и тогда, когда известен истинный закон распределения, но приближенное представление через нормальный закон удобнее для работы.

Плотность распределения при нормальном законе задают следующей формулой:

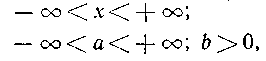
где а и Ь — действительные постоянные, принимающие в каждом случае конкретные значения.

Видно, что распределенная по нормальному закону случайная величина X может изменяться в интервале (-∞, +∞). Встречающиеся на практике случайные величины обычно изменяются в каких-либо конечных интервалах. Это обстоятельство не мешает использованию нормального закона для описания таких случайных величин.

Эта возможность базируется на том, что в конечный интервал длиной 6σ[X] и серединой, совпадающей с m₁ [X], практически попадают все возможные значения распределенной по нормальному закону случайной величины X. В этом мы убедимся дальше.

Постоянные а и b плотности распределения называются параметрами нормального закона и однозначно определяют его.

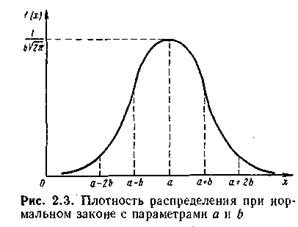
График плотности распределения нормального закона имеет вид, показанный на рис. 2.3.

 

Он симметричен относительно вертикали, отстоящей от начала координат на расстоянии а, имеет максимум в точке х = а, который равен 1/b√(2p), и перегибы в точках х = а — Ь и х = а + Ь. Математическое ожидание m₁[X ] распределенной по нормальному закону случайной величины X можно определить по формуле:

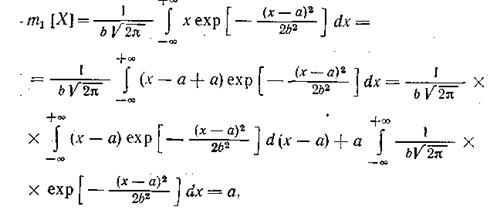
т. е. параметр а нормального закона равен математическому ожиданию m₁[X ] случайной величины X. Аналогично получается

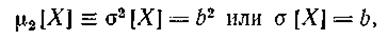
т. е. параметр b нормального закона равен среднему квадратичному отклонению σ[X ] соответствующей случайной величины X.

То, что данная случайная величина X распределена по нормальному закону с математическим ожиданием m₁[X ] и средним квадратичным отклонением σ[X] = Ь, можно записать так: X ~ N (а, Ь).

На рис. 2.4 показана кривая распределения нормального закона для различных значений а и Ь. Изменение параметра а приводит только к перемещению кривой распределения, не изменяя ее формы, поэтому данный параметр называется также центром распределения.

 

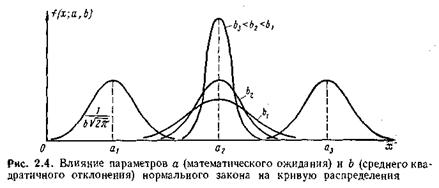
При изменении параметра Ь форма кривой распределения также не изменяется, но изменяется ее масштаб по обеим координатным осям . С уменьшением значения этого параметра увеличивается доля значений случайной величины X, сосредоточенных в окрестности точки х = а, т. е. в окрестности m₁[X ].

Одной из задач, часто решаемых с помощью этого закона распределения, является задача определения вероятности попадания случайной величины X в данный интервал [х1, х2]. “та вероятность

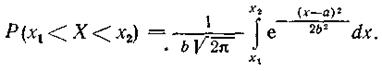
Определенный интеграл в правой части нельзя вычислить точно, так как соответствующий неопределенный интеграл не выражается конечным числом элементарных функций. Для приближенного вычисления интеграла приходится численно интегрировать функцию f(x) или воспользоваться стандартной функцией листа Excel НОРМРАСП(x;среднее;стандартное_откл;интегральная).

Параметры функции: x — значение, для которого строится распределение; Среднее— оценка значения m₁[X ]=а.; Стандартное_откл— оценка значения σ[X] = Ь; Интегральная— логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

 

Для самостоятельного вычисления значения функции F(x) необходимо проинтегрировать функцию f(x) с помощью правила трапеций в интервале от x1=a-3b до x2=x.

 

Практическое задание.

 

Используя индивидуальную базу данных определить характеристики закона нормального распределения.

 

    Порядок выполнения работы

1. Разработать программу для определения

1.1 среднего значения параметров качества;

1.2 среднего квадратичного отклонения параметров качества;

1.3 плотности распределения параметров качества ;

1.4 численного интегрирования функции f.

 

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

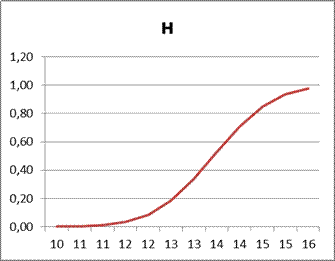
3.1.2. Представить графики функции распределения и плотности параметров качества. (Пример Графики распределения веса велосипедов)

 

 

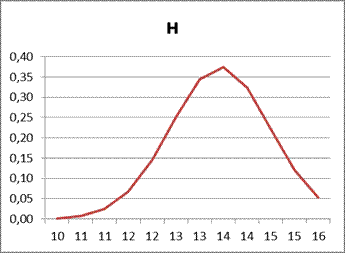
4. Ответить на контрольные вопросы

4.1. Дать определение функции распределения и указать три ее основных свойств.

4.2 Дать определение плотности распределения.

4.3. Записать формулу Ньютона—Лейбница и дать ее геометрическое толкование

4.4 Записать формулу плотности экспоненциального распределения и указать смысл постоянной λ

4.5 Записать формулу плотности при нормальном законе распределения и пояснить смысл, входящих в нее величин.

4.6 Дать определение понятию «квантили случайной величины»

4.7 Показать как изменяется кривая распределения нормального закона для различных значений а и b.

Лабораторная работа № 6 Задача принятия решения на основе многокритериальной оптимизации.

 

Цель Изучения выбора вариантов с использованием множества Парето.

 

Теоретический материал.

 

В задаче принятия решения назовем пару (Ω, Ρ),

где Ω – множество вариантов (альтернатив),

  Р – принцип оптимальности.

Решением задачи является множество 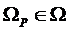, получающееся в соответствии с принципом оптимальности Р.   Отсутствие хотя бы одного из элементов (Ω, Ρ) лишает задачу смысла.

Математическим выражением принципа оптимальности Р служит функция выбора С_р, которая со всеми подмножествами 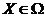 его часть С_р(х). Таким образом, решением исходной задачи является С_р(Ω).

Задача принятия решения различается в зависимости от информации о множестве Ω и принципе оптимальности Р:

1) Общая задача принятия решения: Ω, Р – неизвестны, необходимо 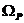 получить в процессе самого решения.

2) Задача с известными Ω называется задачей выбора.

3) Задача, в которой Ω, Ρ – известны называется общей задачей оптимальности.

Во многих задачах при моделировании критерия приходится назначать много критериев. Оказывается, что изменение одного критерия, несёт за собой изменение другого критерия. Существует принципиальная трудность в оценке двух или более вариантов. Особенно если их оценивать безусловно.

Векторная оптимизация:

1) Безусловная оптимизация, когда пытаются определить безусловно лучшее решение, но после этапа безусловной оптимизации можно отсеять заведомо невыгодные решения, т. е. безусловно сравнённые и худшие, поэтому несравнимые, но и не плохие остаются, и мы получаем эффективное множество – множество Парето.

2) Для нахождения наилучшего решения приходится вводить некоторые условия, например, предпочтения или приходится выбирать из всех важных критериев, какой из них самый ценный.

Определение множества Парето

Непрерывный случай.

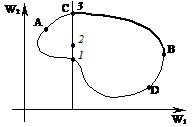Если 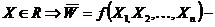множество точек, в котором небольшое улучшение  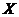влечёт за собой небольшое изменение . Пусть есть два показателя .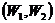

Сравним безусловную пару вариантов: третий безусловно лучше второго и первого. На дуге  находятся лучшие точки при 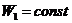, а на дуге  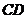лучшие точки при 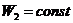. Поэтому точками множества Парето будут являться точки находящиеся на дуге .

 

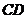 Порядок выполнения работы.

В качестве исходного материала используется таблица параметров качества и цены заданной предметной области (Лабораторная работа №3)

1. Нормирование показателей качества Xi. Нормирование производиться для устранения влияния размерности и диапазона изменения показателя на целевую функцию качества. После нормирования все показатели качества имеют диапазон изменения от 0 до 1. Значение 0 соответствует худшему из возможных значений, а 1- лучшему.

Нормирование производиться по формулам.

1 Если качество возрастает с увеличением значения параметра	2 Если качество уменьшается с увеличением значения параметра
Xni = (Xi - Xmin) / (Xmax - Xmin)	Xni = (Xmax - Xi) / (Xmax - Xmin)
Где Xni-нормированное значение Xi показателя качества, Xmax, Xmin максимальное и минимальное значение Xi показателя качества

2. Выбираются значения персональных оценок весовых коэффициентов. Весовые оценки выбираются в соответствии с приоритетами лица принимающего решение.

№	Сумма оценок	Число передач	Высота подъема руля	Диаметр колес	Вес, кг	Остаточная стоимость через 2-3 года
	1	0,5	0,2	0,1	0,1	0,1

 

3. Определяем значение целевой функции качества F

 

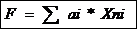для каждого из возможных вариантов выбора, где  ai – весовые коэффициенты, Xni - нормированные значения параметров качества.

4. Составляем множество Парето, т.е. выбираем варианты, где с увеличение цены возрастает и качество. Например, для велосипедов

Модель	Функция качества	Цена, RR
Schwinn Sierra 7	0,266757	10977
KHS	0,429306	13566
Trek Atwood	0,539419	15140
Marin Muirwoods	0,624268	16500
Schwinn Sportera	0,737602	18132
Orbea Anayet	0,83402	35420

 

Содержание отчета

1.Таблица нормированных значений параметров качества.

2. График распределения вариантов выбора в координатах цена-качество

 

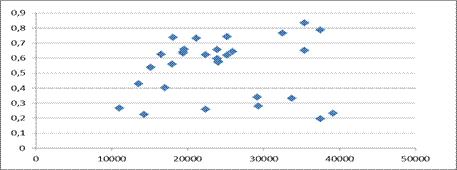
3.Парето оптимальное множество.

 

Контрольные вопросы.

1. Дать определение понятию эффективное множество Парето

2.  Как формировалась функция качества изделия.

 

Работа №7 Оценка вероятности безотказной работы оборудования

 

Цель Разработка программного обеспечения для оценки надежности имеющегося оборудования и принятия решения о его замене.

 

Теоретический материал

 

Принцип практической уверенности

В теории вероятностей и математической статистике чрезвычайно важную роль играют так называемые практически невозможные и практически достоверные события.

Практически невозможным называется такое событие, вероятность которого очень близка к нулю (например, 0,1; 0,05; 0,001 и т. д.).

Практически достоверным называется такое событие, вероятность которого очень близка к единице (например, 0,9; 0,95; 0,99; 0,999 и т. д.).

Очевидно, что если событие А практически невозможное, то его противоположное событие А будет практически достоверным.

Если вероятность одного случайного события 0,4, то предсказать с уверенностью результат опыта при однократном проведении невозможно, но если вероятность события 0,99 или 0,01 это уже становится возможным. В данном случае используем так называемый принцип практической уверенности, сформулировать который можно так: если вероятность появления данного события А очень мала (очень велика), можно быть практически уверенным в том, что при однократном проведении соответствующего опыта событие А не появится (появится). Конечно в таком случае имеется известный риск: событие, которое считаем практически невозможным, может наступить и привести к очень неблагоприятным последствиям. Вероятность α, при которой данное событие можно считать практически невозможным, называется уровнем значимости, а вероятность γ, при которой событие можно считать практически достоверным, называется доверительной вероятностью.

Вопрос о том, насколько мала (велика) должна быть вероятность появления данного события А, чтобы оно считалось практически невозможным (достоверным), выходит за рамки математической теории и в любом отдельном случае решается в соответствии с конкретными условиями и прежде всего со степенью риска, который возникает при появлении (непоявлении) данного невозможного (достоверного) события.

Например, если вероятность «поломки «мышки» в течение одной рабочей смены» равна 0,1. то можно это событие считать невозможным, т. е. пренебречь его появлением и начать работу. Риск в этом случае главным образом связан с уменьшением производительности. Если же вероятность отказа в системе жесткого диска в банке равна 0,1, то совершенно недопустимо считать это событие практически невозможным. В данном случае риск намного больше. Еще больший риск имеется, если принять за практически невозможное событие «отказ бортового компьютера самолета», даже если его вероятность равна 0,001.

Чем больше риск при появлении пренебрегаемого события, тем при меньшей вероятности а нужно считать данное событие практически невозможным. Однако слишком малые численные значения а не всегда оправданы, так как они связаны с удорожанием

При решении технических задач общего характера, где последствия наступления практически невозможных событий не связаны с большими авариями и тяжелыми потерями, принимается  а = 0,1; 0,05 и 0,01 (аналогично у = 0,9; 0,95 и 0,99).

Способы математического описания характеристик надежности

Безотказность объектов можно оценивать следующими основными показателями: средним временем безотказной работы (наработкой на отказ); вероятностью безотказной работы Р (t); интенсивностью отказов λ (t); параметром потока отказов Ω (t).

Среднее время безотказной работы невосстанавливаемых объектов (наработку на отказ) по данным испытаний их на надежность определяют по формуле

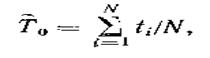
где ti — время исправной работы i-го объекта; N — общее число испытуемых объектов.

Для расчета Т₀ необходимо знать продолжительность исправной работы всех испытуемых объектов.

Наработка до момента отказа t является случайной величиной. Закон ее распределения определяется плотностью вероятности f(t). В тех случаях, когда объекты изготовляют в условиях установившегося производства, а отказы возникают в связи с постепенным изменением параметров при изнашивании и старении, время безотказной работы объектов изменяется по нормальному закону.

Плотность распределения вероятности времени безотказной работы объекта при нормальном распределении описывается уравнением

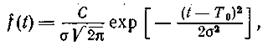
где С — нормирующий множитель; σ — среднее квадратичное отклонение.

Таким образом, нормальный закон характеризуется двумя параметрами: Т₀ и σ. Ввиду ограниченного числа испытаний по полученным данным можно найти лишь статистические оценки этих характеристик и затем с заданной вероятностью α найти доверительные границы, внутри которых должны находиться Т₀ и σ .

При испытаниях фиксируется время наступления отказа: каждого из N объектов, за которыми установлено наблюдение.

В этом

 

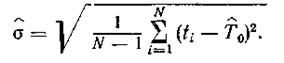
Доверительные границы Т₀ для нормального закона распределения находят из выражений:

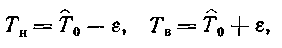
где Тн — нижняя доверительная граница; Тв — верхняя доверительная граница; ε — мера точности, которую определяют из выражения

 

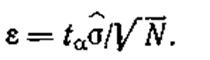
Значения коэффициента tα даны в таблице

Число опытов	Уровень  надежности
	0,8	0,9	0,95	0,98	0,99	0,909
2	3,08	6,31	12,71	31,8	63,7	636,6
3	1,886	2,92	4,3	6,96	9,92	31,6
4	1,638	2,35	3,18	4,54	5,84	12,94
5	1,533	2,13	2,77	3,75	4,6	8,61
6	1,476	2,02	2,57	3,36	4,03	8,86
7	1,44	1,943	2,45	3,14	4,71	5,96
8	1,415	1,895	2,36	3	3,5	5,4
9	1,397	1,86	2,31	2,9	3,36	5,04
10	1,383	1,833	2,26	2,82	3,25	4,78
11	1,372	1,812	2,23	2,76	3,17	4,59
12	1,363	1,796	2,2	2,72	3,11	4,49
13	1,356	1,782	2,18	2,68	3,06	4,32
14	1,35	1,771	2,16	2,65	3,01	4,22
15	1,345	1,761	2,14	2,62	2,98	4,14
16	1,341	1,753	2,13	2,6	2,95	4,'07
17	1,337	1,746	2,12	2,58	2,92	4,02
18	1,333	1,74	2,11	2,57	2,9	3,96
19	1,33	1,734	2,1	2,55	2,88	3,92
20	1,328	1,729	2,09	2,54	2,86	3,88
21	1,325	1,725	2,09	2,53	2,84	3,85
22	1,323	1,721	2,08	2,52	2,83	3,82
23	1,321	1,717	2,07	2,51	2,82	3,79
24	1,319	1,714	2,07	2,5	2,81	3,77
25	1,318	1,711	2,06	2,49	2,8	3,74
26	1,316	1,708	2,06	2,48	2,79	3,72
27	1,315	1,076	2,06	2,48	2,78	3,71
28	1,314	1,703	2,05	2,47	2,77	3,69
29	1,313	1,701	2,05	2,47	2,76	3,67
30	1,311	1,699	2,04	2,46	2,76	3,66
31	1,31	1,697	2,04	2,46	2,75	3,65
41	1,303	1,684	2,02	2,42	2,7	3,55
61	1,296	1,671	2	2,39	2,66	3,46
121	1,289	1,658	1,98	2,36	2,62	3,37

 

Вероятность безотказной работы изделий при нормальном законе распределения

P(t)= 1 – Ф(t).

Гарантированную долговечность определяют по уравнению

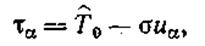
где u_α — квантиль нормального распределения, отвечающий заданному уровню вероятности. Для нормального закона приведены в таблице

Значения квантиля при уровне надежности a.

α	0,9	0,95	0,99	0,999
uα	1,282	1,645	2,326	3,090

 

Практическое задание.

 

Используя индивидуальную базу данных имеющегося оборудования и характеристики закона распределения времени безотказной работы оценить его состояние. Пример реализован на листе «LR5» файла MISPR_Т2.xls.

Порядок выполнения работы

1. Разработать программу для определения:

1.1 доверительных границ;

1.2 вероятности безотказной работы и гарантированную долговечность. табличные данные u_α — квантиль установить в зависимости от категории отдела 1) 0,9, 2) 0,95и 3) 0,99.

1.3 заключения о необходимости замены оборудования в виде списка, отсортированного по мере уменьшения вероятности отказа.

2. Определить вероятность отказа для всех видов оборудования и сравнить ее с гарантированной долговечностью.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2. Представить таблицу с оценкой вероятности отказа для всех видов оборудования и рекомендаций о ее замене.

 

4. Ответить на контрольные вопросы

4.1 Записать формулу определения вероятности попадания случайной величины X в данный интервал [х1, х2] при нормальном законе распределения.

4.2 Записать уравнение плотность распределения вероятности времени безотказной работы объекта при нормальном распределении.

4.3 Дать определение гарантированной долговечности.

4.4 Дать определение вероятности безотказной работы.

 

 

Работа №8. Разработка диагностической СППР на основе нормального законов распределения случайных величин.

 

Цель. Разработка программного обеспечения, для диагностической СППР, на основе нормального законов распределения случайных величин.

 

Теоретический материал.

Вывод данной СППР основывается на обработке законов распределения диагностических параметров. Под диагностическим параметром понимают величину, которую можно измерить и значение которой влияет на диагноз. Например в медицине это возможные анализы. Обучение такой СППР основывается на базе данных, где каждая запись представляет набор диагностических параметров и точный диагноз (причину неисправности).

Журнал диагностики

	Диагностические параметры			Точный диагноз
№	Ток потребления А	Высоковольтное напряжение КВт	Частота развертки Мг	Неисправный блок
1	18	22	30	высоковольтный блок
2	12	15	25	высоковольтный блок
3	11	15	25	высоковольтный блок
4	15	29	10	блок развертки
5	14	29	9	блок развертки
6	14	27	9	блок развертки
7	9	21	15	блок питания
8	10	23	16	блок питания
9	8	19	14	блок питания

 

Из приведенного журнала диагностики видно, что при определенных значениях диагностических параметрах неисправен высоковольтный блок, при других блок развертки и.т.д.

Если определить законы распределения диагностических параметров для каждой неисправности, то можно выяснить наиболее вероятный диагноз (причину неисправности).

 

Порядок выполнения работы

1. Определение характеристик нормального закона распределения диагностических параметров.

Индивидуальная база  данных представляет таблицу «Журнал диагностики мониторов» на листе «BD” файла №варианта.xls.

Первых три столбца, представляют числовые значения диагностируемых параметров в момент выхода монитора из строя. В четвертом указана причина поломки монитора. Пример реализован на листе «LR8» файла MISPR_Т2.xls.

Пронормируем значения диагностических параметров, что позволит унифицировать их диапазон изменения от 0 до 1. (См. лаб.раб. №6)

Необходимо произвести выборку по каждой причине неисправности и определить среднее значение и отклонение параметра.

Таблица 1. Статистические характеристики законов распределения диагностических величин по каждой из неисправностей
	Ток		Напряжение		Частота
Диагноз	М ток	s ток	М напряжение	s нпряжение	М частота	s частота
1 высоковольтный блок	0,8	0,1	0,6	0,2	0,4	0,3
2 блок развертки	0,5	0,3	0,5	0,1	0,6	0,2
3 блок питания	0,3	0,2	0,4	0,1	0,8	0,1

 

Используя данные из таблицы построить графики плотности распределения диагностических параметров для каждой из неисправностей.

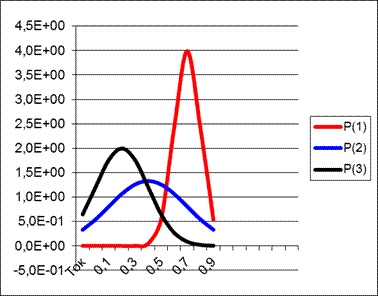Неисправен высоковольтный блок	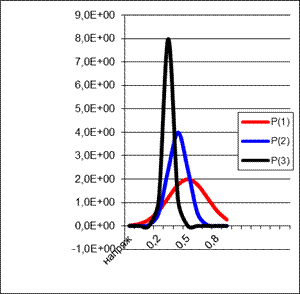Неисправен блок развертки
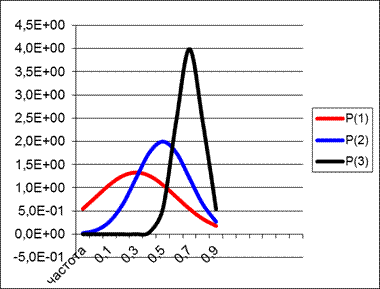Неисправен блок питания

 

Данные графики являются знаниями СППР.

 

В таблице 5 вводятся значения диагностических величин. В таблице 6 производиться вычисления плотности вероятности каждой из неисправностей по данным из таблицы 5. Для окончательной оценки плотности вероятностей суммируются. В таблице 7 представлен блок формирования заключения о наиболее вероятной неисправности монитора.

 

Порядок выполнения работы

1. Разработать программное обеспечение для определения:

1.1 плотности распределения возможных диагнозов по каждой из входных величин.

2. Определить вероятность по каждому диагнозу и сформулировать заключение о наиболее вероятной неисправности.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы.

4. Ответить на контрольные вопросы

4.1 Записать формулу определения индекса вероятности.

 

 

Работа №9. Разработка СППР на основе произвольного закона распределения случайной величины.

 

Цель. Разработка программного обеспечения, для СППР о приобретении необходимого количества расходных материалов, на основе произвольных статистических законов распределения случайных величин.

Индивидуальная база данных представляет таблицу «Журнал замены расходных материалов» на листе «BD” файла №варианта.xls. В нем указаны даты установки и замены катриджей в организации. Также используются данные об установки катриджей в принтеры из таблицы «Существующий парк»

Пример реализован на листе «LR7» файла MISPR_Т2.xls.  

В таблице 1 скопированы данные из «Журнала замены расходных материалов». Определен срок службы каждого катриджа. После чего данные отсортированы по возрастанию.

В таблице 2 определено число групп для обработки данных (2.51), определена ширина каждого класса (2.52). Далее в соответствии с таблицей 2.1 произведена группировка опытных данных. После определения количества элементов в каждой группе стало возможным определить относительную частоту. График относительной плотности распределения fэкс(x)представлен на рис.1, а экспериментальная функция распределения на рис.2. Очевидно, что данное распределение не может быть описано с помощью нормального закона распределения.

В Таблице 3 приведены результаты параболической сплайн интерполяции данных fэкс(x). На каждом этапе коэффициенты a_i,j определяются в соответствии с формулами (2.55). Красным цветом выделен коэффициент a₁₀, значение которого необходимо подобрать. В модуле1 находить функция f(x), которая производит вычисления fрасч(х). Вычисление функции Fтабл. производиться путем численного интегрирования fрасч(х) методом прямоугольников. При интегрировании необходимо подобрать значение Δх таким образом, чтобы конечное значение Fтабл=1. Так в ячейку О38 внесено значение 0,485. На рис.3 представлен график f(x), а на рис. 4 представлен график функции распределения F(x) и его аппроксимация с помощью метода листа «Линия тренда». Полученное уравнение реализовано в функции FF(x).

В таблице 4 первая колонка является копией данных из таблицы «Существующий парк» об установки катриджей в принтеры. Во вторую введена дата окончания расчетного периода, а третья отражает время работы катриджей на  дату окончания расчетного периода. В четвертой определяется вероятность замены каждого катриджа. 

Сумма этих вероятностей и определяет наиболее вероятное количество деталей, вышедших из строя. В данном случае это 22 катриджа.

 

    Порядок выполнения работы

1. Разработать программное обеспечение для определения:

1.1 функции распределения замены расходных материалов

2. Определить количество заменяемых деталей за отчетный период.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы.

4. Ответить на контрольные вопросы

4.1 Записать формулу функции распределения замены расходных материалов

 

Работа №8

Определение значения коэффициента корреляции

 

Используя данные из журнал анализа качества выпускаемой продукции определить значения коэффициентов корреляции между :

1) стоимостью закупаемого в отдел оборудования S и себестоимостью выпускаемой продукции С;

2) стоимостью закупаемого в отдел оборудования S и потерями на ремонт продукции в течении гарантийного срока R;

3) долей работников с высшим образованием K и себестоимостью выпускаемой продукции С;

4) долей работников с высшим образованием K и потерями на ремонт продукции в течении гарантийного срока R.

    Порядок выполнения работы

1. Разработать программу для определения:

1.1 коэффициента корреляции (3.4);

1.2 расчетного значения коэффициента Стьюдента (3.7) его сравнения с табличным значением и формулировкой заключения о пригодности линейной модели.

2. Определить коэффициенты корреляции по четырем зависимостям

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2. Представить таблицу со значениями найденных коэффициентов, расчетных и табличных значений параметра Стьюдента.

4. Ответить на контрольные вопросы

4.1 Записать формулу определения коэффициента корреляции и пояснить смысл всех переменных.

4.2 Записать формулу выборочных дисперсий и пояснить смысл всех переменных.

4.3. Дать определение понятию «значимость коэффициента корреляции»

4.4 Как определить табличное значение параметра Стьюдента.

Работа №9

Определение линейной регрессионной модели

 

Используя данные из журнал анализа качества выпускаемой продукции определить значения коэффициентов линейной регрессионной модели по каждому из отделов между :

1) стоимостью закупаемого в отдел оборудования S и себестоимостью выпускаемой продукции С;

2) стоимостью закупаемого в отдел оборудования S и потерями на ремонт продукции в течении гарантийного срока R;

3) долей работников с высшим образованием K и себестоимостью выпускаемой продукции С;

4) долей работников с высшим образованием K и потерями на ремонт продукции в течении гарантийного срока R.

    Порядок выполнения работы

1. Разработать программу для определения:

1.1 системы уравнений (3.8) используя БД;

1.2 решения системы уравнений (3.8) методом Крамера

1.3 расчетного значения коэффициента Фишера (3.11) его сравнения с табличным значением и формулировкой заключения о пригодности линейной модели.

1.4 определения коэффициента детерминации.

2. Определить линейные модели по четырем зависимостям по каждому из отделов.

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2. Представить таблицу со значениями найденных коэффициентов, расчетных и табличных значений параметра Фишера.

4. Ответить на контрольные вопросы

4.1 Дать пояснения к методу наименьших квадратов и выводу формул (3.8).

4.2 Записать формулу расчетного критерия Фишера и пояснить смысл его составляющих.

4.3. Дать определение понятию «адекватность линейной модели»

4.4 Как определить табличное значение параметра Фишера.

4.5 Дать определение коэффициента детерминации.

Работа №10

Принятие решений по линейной регрессионной модели

 

Используя полученные линейные модели определить по каждому из отделов:

1) стоимость оборудования для снижения затрат на гарантийный ремонт в два раза по сравнению с его средним значением;

2) долю работников с высшим образованием для снижения затрат на гарантийный ремонт в два раза по сравнению с его средним значением

    Порядок выполнения работы

1. Разработать программу для определения:

1.1 необходимых значений входных переменных.

1.2 интервальных оценок ожидаемой величины со степенью 0.95. (3.14), (3.15) и (3.16)

2. Определить значения входных переменных по каждому из отделов..

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2. Представить таблицу со значениями входных переменных и интервальных оценок.

4. Ответить на контрольные вопросы

4.1 Дать пояснения интервальной оценки (3.14)

4.2 Дать пояснения интервальной оценки (3.15)

4.3 Дать пояснения интервальной оценки (3.16)

 

 

Работа №11

Определение линейной регрессионной модели с двумя входными факторами

 

Используя данные из журнал анализа качества выпускаемой продукции определить значения коэффициентов линейной регрессионной модели по каждому из отделов между :

1) стоимостью закупаемого в отдел оборудования S, долей работников с высшим образованием K и себестоимостью выпускаемой продукции С;

2) стоимостью закупаемого в отдел оборудования S, долей работников с высшим образованием K и потерями на ремонт продукции в течении гарантийного срока R;

    Порядок выполнения работы

1. Разработать программу для определения:

1.1 системы уравнений (3.18) используя БД;

1.2 решения системы уравнений (3.8) методом Крамера

1.3 расчетного значения коэффициента Фишера (3.11) его сравнения с табличным значением и формулировкой заключения о пригодности линейной модели.

2. Определить линейные модели по четырем зависимостям по каждому из отделов..

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2. Представить таблицу со значениями найденных коэффициентов, расчетных и табличных значений параметра Фишера.

4. Ответить на контрольные вопросы

4.1 Дать пояснения к методу наименьших квадратов и выводу формул (3.8).

4.2 Записать формулу расчетного критерия Фишера и пояснить смысл его составляющих.

4.3. Дать определение понятию «адекватность линейной модели»

4.4 Как определить табличное значение параметра Фишера.

4.5 Дать определение коэффициента детерминации.

Работа №12

Принятие решений по линейной регрессионной модели

 

Используя полученные линейные модели определить по каждому из отделов:

1) найти коэффициент эластичности по каждому из входных факторов;

    Порядок выполнения работы

1. Разработать программу для определения:

1.1. коэффициентов эластичности

2. Определить значения коэффициентов эластичности по каждой входной  величине по каждому из отделов..

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2. Представить таблицу со значениями коэффициентов эластичности

4. Ответить на контрольные вопросы

4.1 Дать пояснения коэффициенту эластичности и принятию решений на его основе.

 

 

Работа №13

Определение нелинейной регрессионной модели с двумя входными факторами

 

Используя данные из журнал анализа качества выпускаемой продукции определить значения коэффициентов нелинейной регрессионной модели по каждому из отделов между :

1) стоимостью закупаемого в отдел оборудования S, долей работников с высшим образованием K и себестоимостью выпускаемой продукции С;

2) стоимостью закупаемого в отдел оборудования S, долей работников с высшим образованием K и потерями на ремонт продукции в течении гарантийного срока R;

    Порядок выполнения работы

1. Разработать программу для определения:

1.1 системы уравнений (3.18) используя БД;

1.2 решения системы уравнений (3.8) методом Крамера

1.3 расчетного значения коэффициента Фишера (3.11) его сравнения с табличным значением и формулировкой заключения о пригодности линейной модели.

2. Определить линейные модели по четырем зависимостям по каждому из отделов..

3. Составить отчет

3.1 Содержание отчета

3.1.1. Представить блок схему программы

3.1.2. Представить таблицу со значениями найденных коэффициентов, расчетных и табличных значений параметра Фишера.

4. Ответить на контрольные вопросы

4.1 Дать пояснения к методу наименьших квадратов и выводу формул (3.8).

4.2 Записать формулу расчетного критерия Фишера и пояснить смысл его составляющих.

4.3. Дать определение понятию «адекватность линейной модели»

4.4 Как определить табличное значение параметра Фишера.

4.5 Дать определение коэффициента детерминации.

 

 

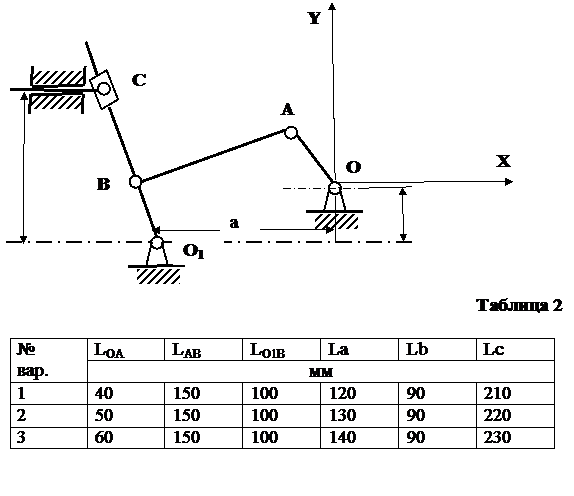
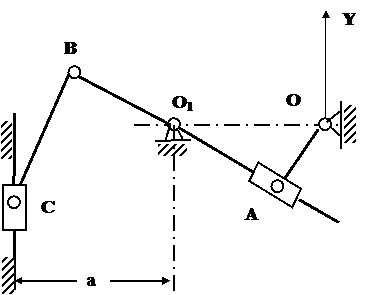
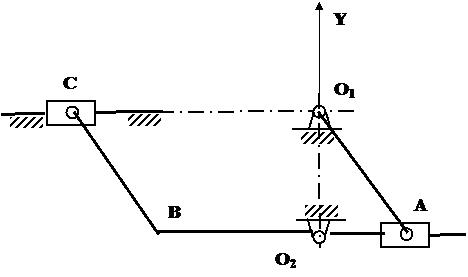
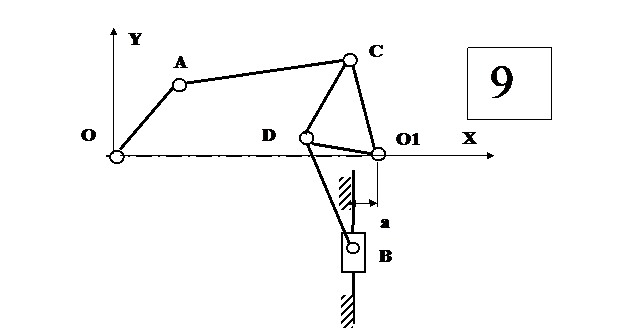
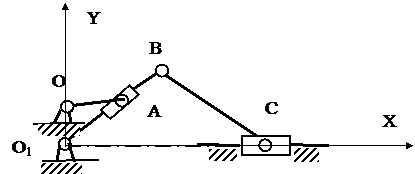
Приложение 1

Схемы механизмов

 

6

Таблица 1 № вар. LOA LAC LOO1 LOB LO1A LO1D LCD LAT мм 1 60 120 100 150 100 130 60 50 2 80 300 250 350 150 100 60 200 3 50 160 150 200 100 120 40 80

8

Таблица 2 № вар. LOA LOO1 LO1B LBC La мм 1 100 200 120 80 130 2 80 150 100 70 120 3 150 300 200 140 250

X

Таблица 1 № вар. LOA= LAM= LMT LAB LOO1 LBC LO1C LCD LDE мм 1 80 250 360 125 120 220 40 2 90 250 510 225 135 200 50 3 100 300 590 250 150 230 50

10

Таблица 2 № вар. LO1O2 LO1A LO2B LBC мм 1 120 250 200 600 2 60 200 180 500 3 110 240 220 600

X

Таблица 1 № вар. LOA LAC LOO1 LCO=LDO1 LDC LDB La мм 1 60 180 225 120 140 250 100 2 70 200 260 150 170 300 100 3 80 250 300 150 190 350 150

12

Таблица 2 № вар. LOA LO1B LBC LOO1 мм 1 80 140 400 40 2 100 160 450 30 3 250 400 1000 100

Таблица 1 № вар. LOA LAT=LO1D LO1C LCB La Lb мм 1 140 65 50 150 5 15 2 240 120 150 400 15 40 3 180 85 100 300 10 30   Дата добавления: 2018-05-12; просмотров: 299; Мы поможем в написании вашей работы! Поделиться с друзьями: Мы поможем в написании ваших работ! . . © 2014-2024 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (1.216)