Практикум по вычислительной математике

Лабораторные работы для Mathcad 2001i Professional

Лабораторная работа № 1
Обращение матриц

 

Задача.1. Данную квадратную матрицу A разбить на произведение двух треугольных матриц T1 и T2. 2. Для каждой из полученных матриц (T1 и T2) найти обращенную (T1^-1 и T2^-1соответственно), т.е. такую, чтобы произведение исходной матрицы и обращенной давало единичную (например, T1*T1^-1=E). Произведение обращенных матриц должно давать обращенную матрицу
 A (T2^-1*T1^-1=A^-1). т.е. необходимо посчитать A^-1, перемножив T1^-1 и T2^-1,и посчитать A^-1 с помощью функций MathCAD. Результаты сравнить.

Решение.1. Задается исходная матрица A и треугольные матрицы T1 и T2, т.к. в матрицах T1 и T2 коэффициенты неизвестны, то необходимо указать, что эти матрицы зависят от коэффициентов. C клавиатуры вводится имя матрицы, знак присваивания вводится нажатием клавиши  на панели Evaluation или клавишей “:”, матрица вводится нажатием клавиши  на панели Matrix.  Количество строк и столбцов задается равным 4. Ввод нижнего индекса осуществляется с помощью клавиатуры следующим образом: нажимается клавиша “[”, вводится индекс, заканчивается ввод нажатием клавиши “→”. (Нумерация элементов матриц и векторов в MathCAD начинается с нуля).

Теперь выражаются формулы для расчета элементов треугольных матриц. Для этого необходимо посчитать произведение T1 и T2в символьном (аналитическом) виде. Ниже введенных матриц выводится это произведение. С клавиатуры вводится выражение T1(b)*T2(b), вводится оператор символьного вывода нажатием клавиши  на панели Symbolic, нажимается “Enter”.

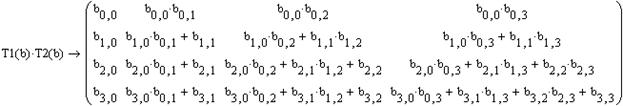
Далее из уравнения  T1(b)*T2(b)=A каждый элемент полученного символьного произведения матриц должен быть равен соответствующему элементу матрицы A. Например, для нулевого столбца необходимо реализовать цикл i от 0 до 3, и всем присвоить b_i,0=a_i,0. Это действие выполняется в столбик. С клавиатуры вводится имя циклически изменяемой переменной, знак присваивания, пределы изменения нажатием клавиши  на панели Matrix. Ниже операция присваивания. Для проверки можно вывести значения найденных величин. Знак численного вывода вводится клавишей  на панели Evaluation.

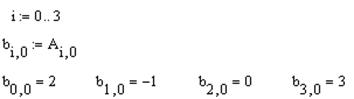
Аналогичным образом вычислить самостоятельно значения остальных коэффициентов для:

j от 1 до 3 b_0,j:=A_0,j/b_0,0 в нулевой строке;

i от 1 до 3 b_i,1:= A_i,1-b_i,0*b_0,1 в первом столбце;

 j от 2 до 3 b_1,j:= (A_1,j-b_1,0*b_0,j)/ b_1,1 в первой строке;

i от 2 до 3 b_i,2:= A_i,2-b_i,0*b_0,2-b_i,1*b_1,2 во втором столбце;

b_2,3:= (A_2,3-b_2,0*b_0,3-b_2,1*b_1,3)/ b_2,2 ;         b_3,3:= A_3,3- 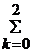b_3,k*b_k,3.

Скобки можно ввести c клавиатуры или клавишей  на панели Calculator. Операция суммирования вводится клавишей  на палении Calculus. Теперь производится вывод треугольных матриц и проверка правильности нахождения их элементов.

Если произведение получилось равным исходной матрице A, то элементы найдены верно.

2. Обращение матрицы T1. Вводится новая матрица TT1.

.

Производится символьное умножение.

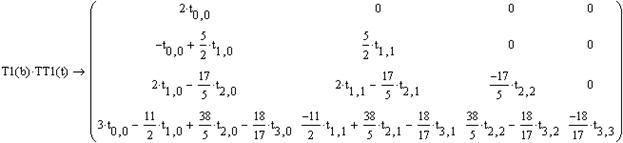
Вычисляются коэффициенты обращенной матрицы сначала на главной диагонали затем вниз от нее:

1) для i от 0 до 3 t_i,i=1/b_i,I ;

2) для i от 1 до 3 t_i,i-1=-t_i-1,i-1*b_i,i-1/b_i,I ;

3) для i от 2 до 3 t_i,i-2=-(t_i-2,i-2*b_i,i-2+t_i-1,i-2*b_i,i-1)/b_i,I ;

4) t_3,0= -( 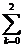b _3,k*t _k,0)/b_3,3 .

Проверка правильности вычислений.

Матрицу T2 обратить самостоятельно. Обращенную матрицу представить в виде

Если символьно перемножить T2 и TT2, получится матрица вида (при выполнении работы не выводить):

.

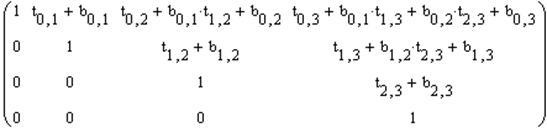Из условия, что все ее элементы, лежащие выше главной диагонали, должны быть равны нулю, и, зная все коэффициенты b_i,j, вывести формулы для нахождения неизвестных коэффициентов t_ij. Использовать циклы и знак суммирования.

Для обращения матрицы с помощью MathCAD на свободном месте документа вводится имя матрицы, знак обращения клавишей  на панели Matrix, и знак численного вывода.

Лабораторная работа №2
Решение системы нелинейных уравнений

 

Задача.Данную систему нелинейных уравнений решить несколькими методами. 1) методом итераций; 2) методом Ньютона; 3) с помощью функций MathCAD. Результаты сравнить. Каждый пункт задания выполнять в отдельном документе. Точность решения принять равной 10^-3.

Решение.1. Задаются уравнения. C клавиатуры вводится имя переменной, в которую заносится уравнение, вводится левая часть, ставится знак равенства клавишей  на панели Boolean, вводится правая часть. Греческие буквы вводятся с помощью панели Greek. Возведение в степень осуществляется с помощью знака “^” (10^-3) или клавиши  на панели Calculator.

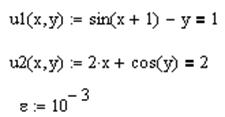
Теперь выражаются искомые переменные. Их надо выразить обе, по одной из каждого уравнения. Получатся две функции, каждая из которых будет зависеть только от одной переменной. С клавиатуры вводится имя функции, ставится знак присваивания, на панели Symbolic нажимается клавиша , слева от появившейся функции «■solve, ■» пишется имя уравнения, справа – выражаемая переменная. Нажимается ввод.

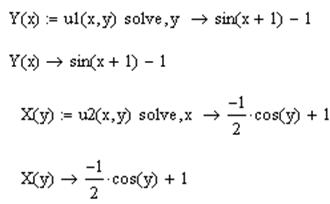
Далее графическим способом определяются начальные приближения. Для построения графика на панели Graph нажимается клавиша , появляется шаблон графика. Для горизонтальной оси (под графиком) вводится «x,X(y)», для вертикальной оси (слева от графика) – «Y(x),y». При вводе этих значений появятся поля для ввода предельных значений абсциссы и ординаты, которые можно не указывать (по умолчанию – от -10 до 10), но потом их можно будет изменить. Нажимается «Enter».

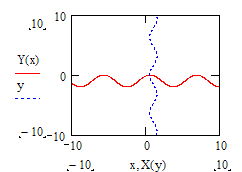
Для более точного определения координаты точки пересечения графиков требуется: а) щелкнуть по графику левой клавишей мышки (войти в график); б) на панели Graph нажать клавишу , откроется окно X-Y Zoom;
в) расположить это окно так, чтобы оно не закрывало рисунок; г) держа нажатой левую клавишу мыши, выделить на графике область пересечения графиков (в полях окна X-Y Zoom отобразятся координаты выделенной области); д) нажать последовательно клавиши  и  в окне X-Y Zoom; е) теперь, когда область пересечения графиков функций увеличена, необходимо войти в график и нажать клавишу  на панелиGraph; ж) Открывшееся окно X-Y Trace расположить так, чтобы оно не закрывало рисунок; з) левой клавишей мыши щелкнуть в месте пересечения графиков. В полях окна X-Y Trace появятся значения координат в месте щелчка. Эти координаты следует взять в качестве начального приближения .Окно X-Y Trace можно закрыть.

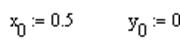
Далее организовывается итерационный цикл.

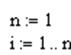
Такие циклы MathCAD обрабатывает только в числовом виде, поэтому , искомым переменным необходимо сначала присвоить числовые значения, например нулевые, затем просчитать значения итерационные.

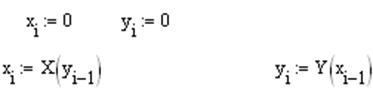
После этого цикла оценивается погрешность и выводятся все найденные значения. Знак квадратного корня ставится нажатием клавиши  на панели Calculator. Возведение в квадрат можно поставить нажатием клавиши  на той же панели.

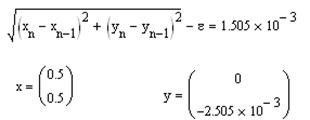
Если выведенная разность отрицательна, то точность достигнута, если она положительна, то необходимо вернуться к началу цикла (n:=..) и увеличить значение n на единицу (Например, вместо n:=1 написать n:=2). И так до тех пор, пока не будет достигнута точность.

2. Для решения методом Ньютона создается новый документ, а в уравнениях системы все слагаемые переносятся в одну сторону и уравнения системы задаются как функции двух переменных.

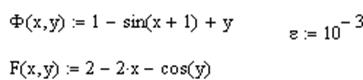
Задаются еще две функции и начальные приближения. Числитель и знаменатель каждой дроби ставится так: вводится знак определителя нажатием клавиши  на панели Matrix, внутри него ставится матрица 2х2. Оператор дифференцирования вводится нажатием клавиши 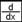 на панели Calculus.

Как и в первом методе организуется итерационный цикл, оценивается погрешность и выводятся найденные значения. Если точность не будет достигнута, то в начале цикла n увеличивается на 1.

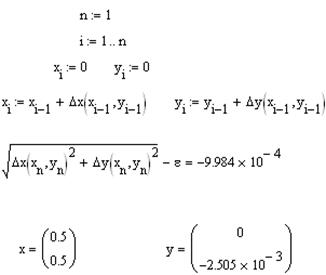
3. И наконец, система уравнений решается с помощью функций MathCAD. В новом документе задаются начальные приближения;

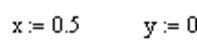
Пишется ключевое слово   и ниже него система уравнений;

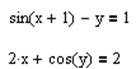
После этого решение находится с помощью функции Find:

.

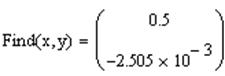Лабораторная работа №3
Построение уравнений регрессии

 

Задача.Для данного набора точек на плоскости построить методом наименьших квадратов кривую, наименее от них отклоняющуюся, нескольких видов: 1) полиномиальная регрессия; 2) гиперболическая регрессия;
3) степенная регрессия; 4) показательная регрессия. Для данного набора точек в пространстве построить методом наименьших квадратов поверхность, наименее от них отклоняющуюся, нескольких видов: 5) линейная регрессия;
6) экспоненциальная регрессия; 7) квадратичная регрессия. Для каждой кривой (поверхности) рассчитать остаточную дисперсию. Посмотреть, в каком случае она будет минимальной.

Решение.1. Полиномиальная регрессия представляется в виде . Дисперсия для нее рассчитывается как .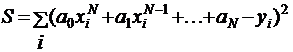

Для определения коэффициентов a_i, при которых отклонение будет минимальным, необходимо по каждому из них взять производную:

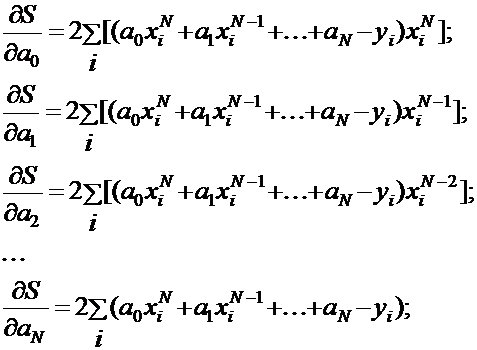
и приравнять ее к нулю для получения системы уравнений:

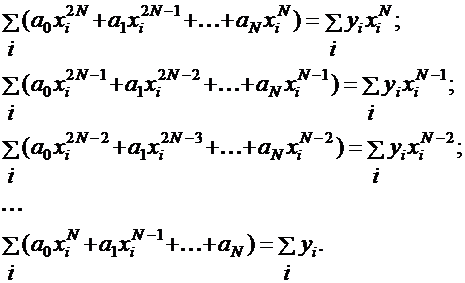
Для решения задачи в MathCAD сначала требуется задать векторы точек:

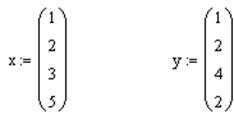
Затем определить количество точек и степень полинома.

Коэффициенты левой и правой частей системы уравнений вычисляются в двойном цикле.

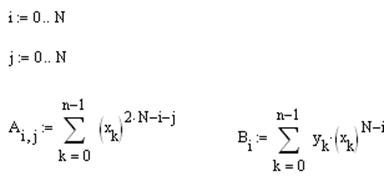
Решается система уравнений.

Теперь задается полином.

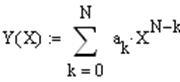
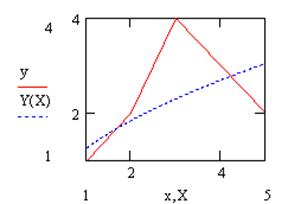
Далее строится график и рассчитывается остаточная дисперсия.

Формула для расчета остаточной дисперсии для всех случаев на плоскости будет одинаковой.

2. Гиперболическая регрессия представляется в виде 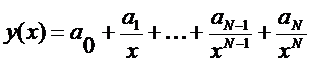. Реализовать самостоятельно.

3. Построение уравнения степенной регрессии выполняется в новом документе. Сначала, как в первом случае, задаются векторы точек и вычисляется их количество.

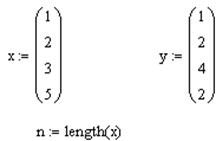
Степенная регрессия представляется в виде 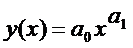. Для нее дисперсия рассчитывается по формуле 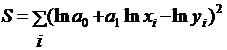, которая получается логарифмированием обеих частей. Если взять производные по коэффициентам и приравнять их к нулю, получится система уравнений:

ее коэффициенты в MathCAD вычисляются по формулам:

.

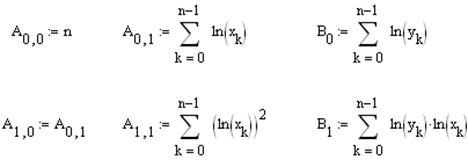Решается система уравнений.

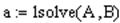
В результате решения системы были найдены величины ln(a₀) и a₁, поэтому необходимо посчитать значение a₀:

,

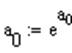теперь можно посмотреть найденные величины:

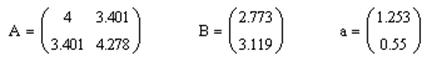
Задается степенная функция.

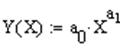
Строится график и рассчитывается остаточная дисперсия.

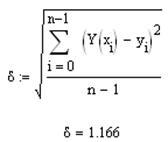
4. Показательная регрессия представляется в виде 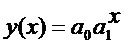. Реализовать самостоятельно.

5. Линейная регрессия в пространстве представляется в виде . Дисперсия для нее вычисляется по формуле 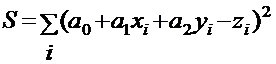. Для определения коэффициентов a_i берутся частные производные:

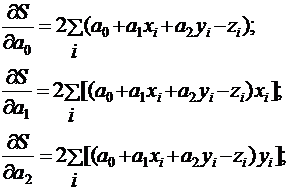
которые приравниваются к нулю. Получается система уравнений:

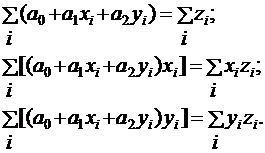
Исходные данные для построения поверхности задаются в виде векторов и определяется количество точек.

Коэффициенты системы в MathCAD вычисляются по формулам:

.

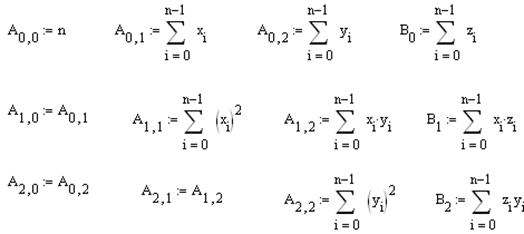Теперь решается система уравнений и выводятся найденные величины.

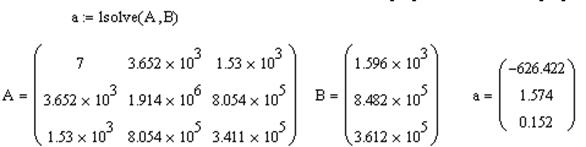
Далее задается уравнение поверхности.

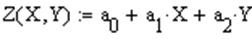
Строится ее график. На панели Graph нажимается клавиша   и внизу появившегося шаблона пишется Z. График можно вращать, водя по нему указатель мыши при нажатой левой клавише.

И, наконец, находится остаточная дисперсия.

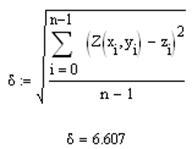
6. Экспоненциальная регрессия представляется в виде 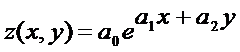. Формула дисперсии получается логарифмированием обеих частей и суммированием по всем точкам:

Снова берутся производные по коэффициентам a_i и приравниваются к нулю:

Снова задаются исходные данные для построения поверхности и количество точек.

В MathCAD коэффициенты этой системы вычисляются по формулам:

.

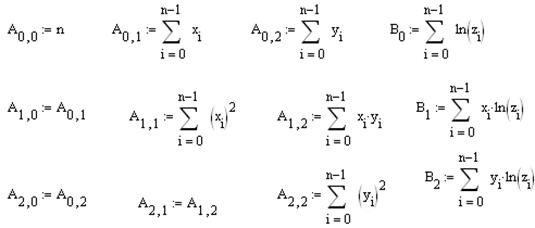Потом решается система:

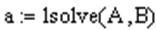
В результате решения системы были найдены величины ln(a₀), a₁, a₂; поэтому необходимо посчитать значение a₀:

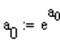
Теперь можно посмотреть найденные величины.

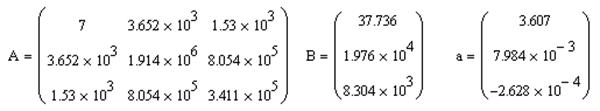
Задается уравнение поверхности.

.

Рассчитывается остаточная дисперсия:

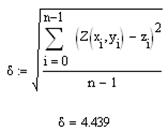
7. Квадратичная регрессия для двух переменных представляется в виде: 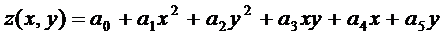. Реализовать самостоятельно.

 

Лабораторная работа № 4
Разложение функций в ряд Фурье пополиномам Лежандра

 

Задача.Разложить в ряд Фурье по полиномам Лежандра функции: 1) полиномиальную непрерывная функция, 2) неполиномиальную функцию, непрерывную на [-1;1], 3) функцию, имеющую  разрыв 1-го рода. Для каждого разложения посчитать среднеквадратичное отклонение и среднеквадратичное уклонение, построить графики.

Решение.1. Сначала задается раскладываемая функция, требуемая точность и формула для вычисления коэффициентов разложения, в которую входит встроенная функция Leg(n,x), возвращающая полином Лежандра n-ой степени, который вычисляется по формуле 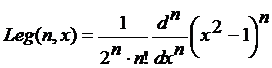. Определенный интеграл в последнем выражении вводится нажатием клавиши  на панели Calculus.

Далее определяется максимальное число слагаемых, необходимых для наилучшего приближения функции. Вводится имя переменной, ставится знак присваивания. Далее вводится программный модуль. Для него требуются четыре строки. Для добавления строк служит клавиша  на панели Programming, т.е. к имеющейся одной необходимо добавить еще три. Для этого данная клавиша нажимается трижды. Внутри программного модуля знак присваивания «←» вводится нажатием клавиши  панели Programming.На третьей строке модуля стоит цикл с предусловием. Он вводится нажатием клавиши   на панели Programming. В теле цикла добавляется еще одна строка.

Вычисляется среднеквадратичное отклонение:

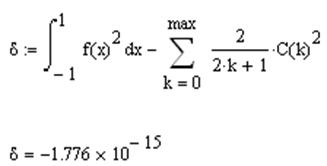
Составляется разложение функции:

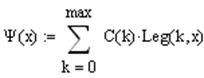
Потом находится среднеквадратичное уклонение:

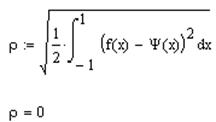
И, наконец, строится график.

2. Для неполиномиальной непрерывной функции алгоритм будет таким же. Выполнить самостоятельно.

3. Функция, имеющая 1 разрыв 1-го рода задается так: вводится ее имя, ставится знак присваивания, добавляется одна строка. В начале каждой строки задается значение функции, нажатием клавиши  на панели Programming вводится условный оператор. Логические операторы сравнения «≤» и «≥» вводятся нажатием клавиш  и  соответственно на панели Boolean.Например:

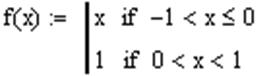
Точность вычислений взять равной 10^-2. Далее весь алгоритм такой же, как в первом случае. Реализовать самостоятельно.

Лабораторная работа № 5
Решение дифференциального уравнения второго порядка

 

Задача.Решить дифференциальное уравнение второго порядка с краевыми условиями методом прогонки. Построить график.

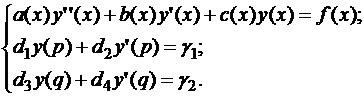
Решение.Перед тем как решать уравнение методом прогонки, над его левой частью необходимо выполнить некоторые преобразования. В MathCAD ее можно представить в виде функции:

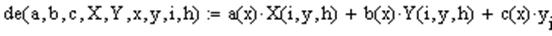
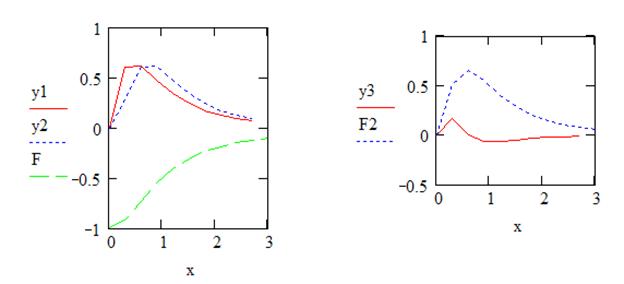
где X(i,y,h)=y’’ и Y(i,y,h)=y’. Первая и вторая производные задаются через апроксимационные формулы:

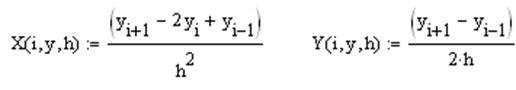
После чего левая часть принимает вид:

.

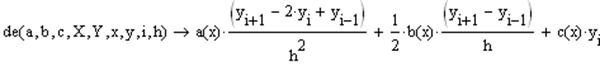Теперь осуществляется приведение к общему знаменателю.

.

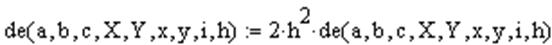Далее необходимо относительно h (шага по x) раскрыть скобки. С клавиатуры вводится имя функции, знак присваивания, на панели Symbolic нажимается клавиша , слева от появившейся функции  «■expand, ■» вводится имя выражения, в котором раскрываются скобки, справа - имя переменной. Нажимается ввод. Внимание! Новая функция уже не зависит отXи Y.

.

Приводятся подобные. С клавиатуры вводится имя функции, знак присваивания, на панели Symbolic нажимается клавиша , слева от появившейся функции  «■ collect, ■» вводится имя выражения, в котором приводятся подобные, справа через запятую - имена переменных, по которым собираются подобные. Нажимается ввод.

.

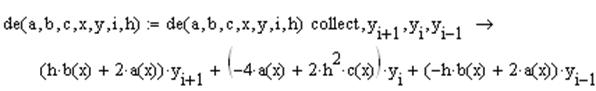Получен окончательный вид левой части. Теперь можно ввести условие задачи:

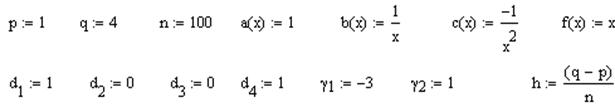
После этого в цикле вычисляются пошаговые значения x и коэффициенты трехдиагональной матрицы:

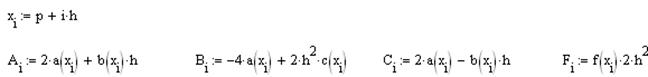
Определяются начальные прогоночные коэффициенты:

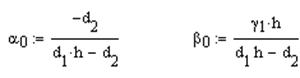
После чего в цикле находятся все остальные прогоночные коэффициенты:

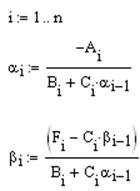
Теперь можно определить значение функции в конце интервала.

Далее в обратном цикле вычисляются все значения искомой функции.

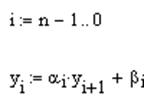
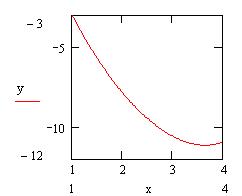
Строится график.

 

Лабораторная работа № 6
«Аппроксимации»

 

1. Кусочно-линейная аппроксимация

Задача: Построить по заданным точкам ломанную линию.

Решение: Задается набор точек, и вычисляется их количество.

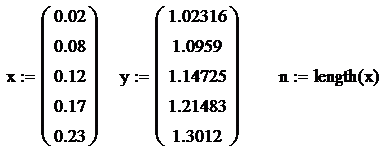
Каждые две соседние точки соединяются прямыми вида y=ax+b, для каждой из которых находятся коэффициенты a и b.

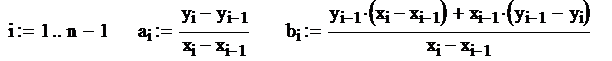
Задается функция

.

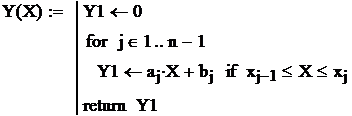Строится график

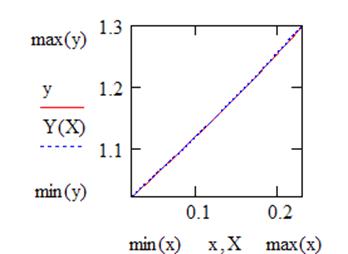
2. Кусочно-квадратичная аппроксимация

Лабораторная работа № 7
Решение СЛАУ с помощью LU разложения

 

Задача. Решить систему линейных алгебраических уравнений с помощью LU разложения.

Решение. Задается матрица коэффициентов A, вектор правой части B, а также матрицы L и U, которые будут в дальнейшем разложением исходной матрицы A. C клавиатуры вводится имя матрицы, знак присваивания вводится нажатием клавиши 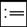 на панели Evaluation или клавишей [:], матрица вводится нажатием клавиши  на панели Matrix.Количество строк и столбцов задается равным 4. Ввод нижнего индекса осуществляется с помощью клавиатуры следующим образом: нажимается клавиша [ [], вводится индекс, заканчивается ввод нажатием клавиши [→]. (Нумерация элементов матриц и векторов в MathCAD начинается с нуля).

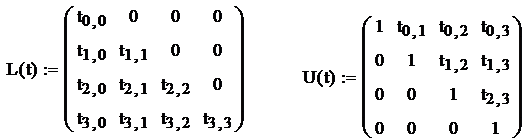
Теперь выражаются формулы для расчета элементов треугольных матриц. Для этого необходимо посчитать произведение L и Uв символьном (аналитическом) виде. Ниже введенных матриц выводится это произведение. С клавиатуры вводится выражение L(t)*U(t), вводится оператор символьного вывода нажатием клавиши  на панели Symbolic, нажимается Enter.

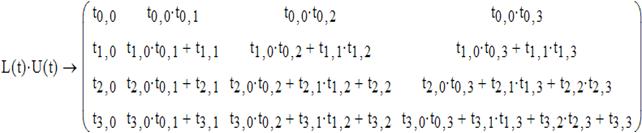
Далее из уравнения L(t)*U(t)=Aприравниваемкаждый элемент полученного символьного произведения соответствующему элементу матрицы A.

Например, для нулевого столбца необходимо реализовать цикл для i от 0 до 3, и в нем присвоить t_i,0=A_i,0. Это действие выполняется в одной строке. С клавиатуры вводится имя циклически изменяемой переменной, знак присваивания, пределы изменения нажатием клавиши  на панели Matrix. Ниже операция присваивания. Для проверки можно вывести значения найденных величин. Знак численного вывода водится клавишей  на панели Evaluation.

.

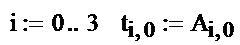Аналогичным образом вычисляются значения остальных коэффициентов для:

j от 1 до 3 t_0,j:=A_0,j/t_0,0 и t_i,1:= A_j,1-t_j,0*t_0,1;

 j от 2 до 3 t_1,j:= (A_1,j-t_1,0*t_0,j)/t_1,1 и t_i,2:= A_j,2-t_j,0*t_0,2-t_j,1*t_1,2;

, ,

.

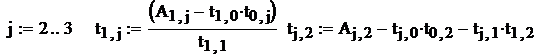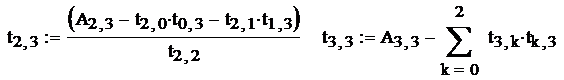Скобки можно ввести c клавиатуры или клавишей  на панели Calculator. Операция суммирования вводится клавишей  на палении Calculus.

.

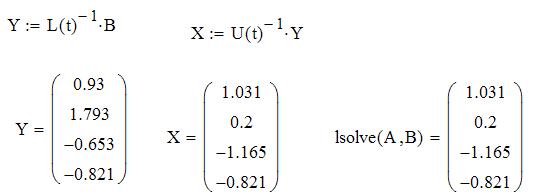Лабораторная работа № 8
Численное интегрирование

 

Задача. Найти определенный интеграл от функции различными способами.

Решение. Зададим функцию и пределы интегрирования.

       

 

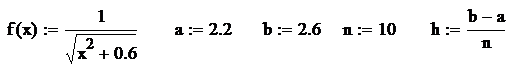
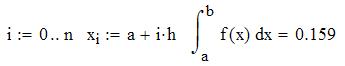
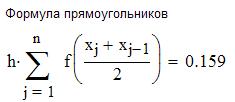
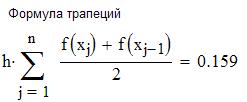
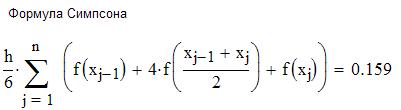
Лабораторная работа № 9
Обращение клеточной матрицы

 

 

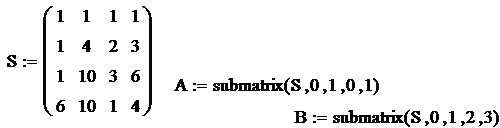
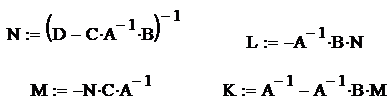
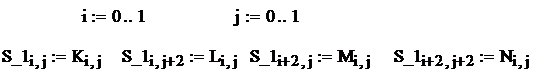
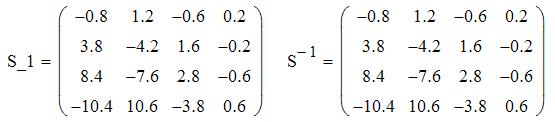
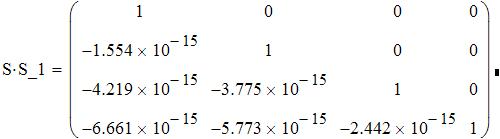
Лабораторная работа № 10
Метод итераций

 

.

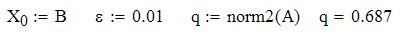
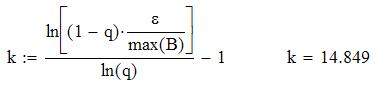
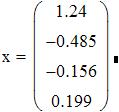Лабораторная работа № 11
Метод прогонки

 

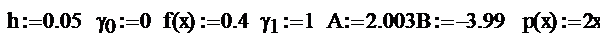
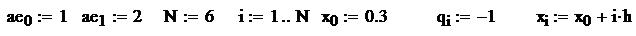
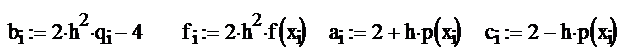
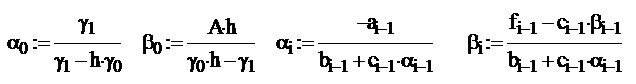
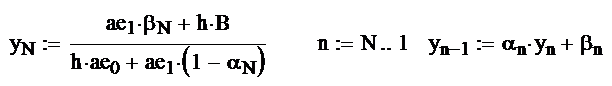
Лабораторная работа № 12
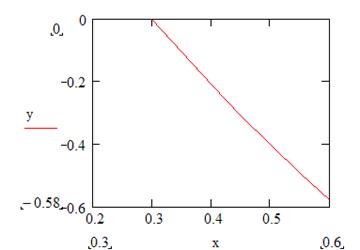
Метод Рунге-Кутта

 

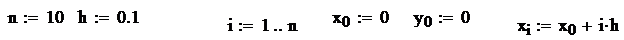
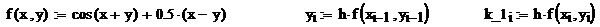
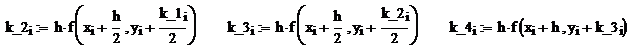
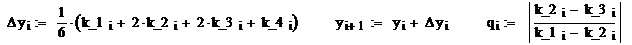
Лабораторная работа № 13
Метод сеток для уравнения теплопроводности

 

 

 

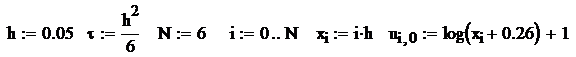
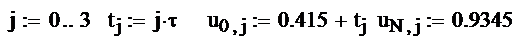
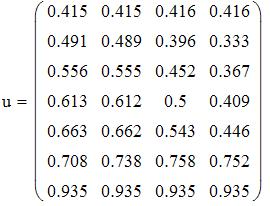
Лабораторная работа № 14
Полином Лагранжа

 

 

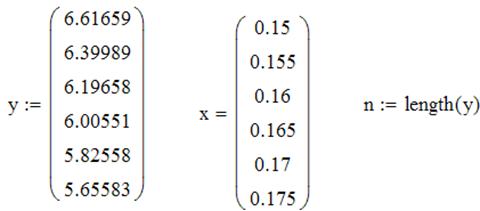
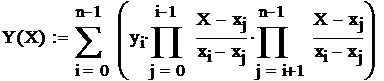
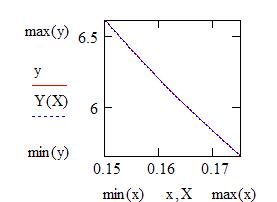
Лабораторная работа № 15
Численное дифференцирование

---

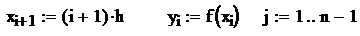
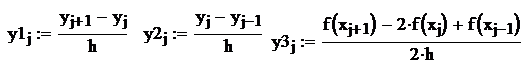
Дата добавления: 2018-05-12; просмотров: 517; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

⇐ Предыдущая891011121314151617Следующая ⇒

---

Мы поможем в написании ваших работ!