Раздел 1. Структура оптимизационной модели. Классификация моделей.
Российский государственный университет им. И. Канта
Математические методы и модели в управлении и финансах
Учебное пособие для студентов всех форм подготовки, обучающихся по специальностям и направлениям на экономическом факультете РГУ
Калининград
200Х
Учебное пособие содержит теоретический и практический материал курса, задания для контрольных работ, методические рекомендации по их выполнению, а также список рекомендуемой литературы.
Составитель: к.э.н., доц. С. Э. Солдатова
Печатается по решению редакционно-издательского Совета Российского государственного университета им. И. Канта
© Издательство РГУ, 200Х
СОДЕРЖАНИЕ
Введение………………………………………………….
Раздел 1. Структура оптимизационной модели. Классификация моделей.
Раздел 2. Линейное программирование.
Раздел 3. Нелинейное программирование
Раздел 4. Динамическое программирование
Раздел 5. Основы теории игр
Раздел 6. Основы теории управления запасами
Раздел 7. Основы теории систем массового обслуживания
Заключение
Задания для индивидуальной и самостоятельной работы
Список литературы
Введение
Настоящее учебное пособие является вспомогательным средством изучения научных и учебных дисциплин, базирующихся на курсах математического программирования и исследования операций. Его основное содержание – математические модели и алгоритмы поиска оптимальных управленческих решений.
|
|
|
Содержание пособия связано с теоретическими и прикладными курсами, включенными в учебные планы подготовки специалистов, бакалавров и магистрантов на экономическом факультете РГУ им. И. Канта. Его концептуальная основа базируется на экономической теории, прикладная ориентация задается теорией принятия решений, а спектр возможных приложений охватывает разнообразные сферы деятельности выпускника экономического факультета, например, построение математической модели объекта, принятие текущих или перспективных решений в сфере планирования, финансов и т.д.
Управление любой организационной системой предполагает, что при решении возникающих проблем субъект управления сталкивается с достаточно большим количеством альтернатив. Для рационализации процесса поиска и обоснования наиболее приемлемого (а, возможно и оптимального) решения субъект управления должен располагать определенными алгоритмами. Применение математически обоснованных алгоритмов требует умения представлять управляемый процесс или ситуацию в виде математической модели.
В рассматриваемом курсе поиск оптимального управленческого решения трактуется как решение многомерной экстремальной задачи с ограничениями, то есть задачи на экстремум функции многих переменных с ограничениями на область изменения этих переменных. Функция, экстремальное значение которой требуется найти, именуется целевой или критерием оптимальности. Экономические возможности формализуются в виде системы ограничений, имеющих вид равенств или неравенств. Моделирование экономического процесса или управляемого объекта в таком виде означает, что все параметры, характеризующие как сам процесс, так и внешние условия должны быть количественно определены, измерены.
|
|
|
Основная цель пособия – содействовать развитию профессиональных компетенций, связанных с математическим описанием объекта управления и количественным обоснованием выбора наиболее эффективных управленческих решений. В русле ее реализации решались следующие задачи:
- ознакомить читателей с математическим аппаратом, применяемым в моделировании экономических и управленческих ситуаций;
- проиллюстрировать применение основных методов построения моделей экономических и управленческих ситуаций на примерах;
|
|
|
- показать возможности выбора оптимальных управленческих решений с помощью математического программирования и исследования операций.
Автор полагает, что в результате изучения пособия читатель получит возможность:
- овладеть навыками самостоятельной аналитической, проектной и исследовательской деятельности, основанными на математической подготовке;
- приобрести умения:
- формулировать и решать задачи, возникающие в ходе профессиональной деятельности, используя методы математики и исследования операций;
- выбрать необходимые математические методы исследования, исходя из задач конкретного проекта;
- обрабатывать полученные результаты, анализировать и осмысливать их с учетом имеющихся данных;
- ставить и решать задачи в области своей профессиональной компетенции, опираясь на навыки математического моделирования;
- системно анализировать тенденции и конкретные ситуации в области общего, стратегического и функционального менеджмента, используя математические модели;
- владеть методическим аппаратом, позволяющим исследовать, анализировать и прогнозировать явления в области менеджмента и финансов с помощью математических моделей;
|
|
|
- разрабатывать и реализовывать междисциплинарные проекты, связанные с задачами менеджмента, используя математические модели.
Структура пособия задается требованиями, заложенными в образовательные программы подготовки специалистов, бакалавров и магистров на экономическом факультете РГУ. Логика изложения материала определяется последовательностью, заложенной в традиционные курсы математического программирования и исследования операций.
Раздел 1. Структура оптимизационной модели. Классификация моделей.
Абсолютное большинство проблемных ситуаций в управлении, экономике или финансовой сфере предполагают наличие множества альтернативных вариантов их решения. Рациональный подход к управлению, основанный на фундаментальном экономическом тезисе об ограниченности ресурсов, требует выбора наилучшего ( оптимального ) из возможных решений. Использование математических инструментов и методов, при наличии определенных предпосылок, позволяет превратить поиск оптимальных решений в целенаправленный и экономный процесс.
Обязательным предварительным условием использования математического алгоритма поиска оптимального решения является представление проблемной ситуации в виде математической модели. Модель должна отражать целевую установку лица, принимающего решение, а также структуру проблемной ситуации, в которой выделяются две категории факторов – подконтрольных и неподконтрольных лицу, принимающему решение. Само решение воплощается в выборе качественных и количественных характеристик управляемых, подконтрольных факторов, однако сам выбор изначально предполагает наличие ограничений в виде совокупности внешних, неуправляемых и неподконтрольных факторов.
Математическим описанием совокупности управляемых факторов в оптимизационной модели является вектор инструментальных переменных, для обозначения которого мы будем использовать символ x. Элементами данного вектора будут инструментальные переменные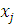 
, каждая из которых соответствует количественному значению некоторого подконтрольного фактора. Число этих факторов будем обозначать символом n.Таким образом, можно записать
x =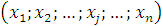 
Целевую установку лица, принимающего решение, обозначим как целевую функцию, или критерий оптимальности. Обозначим ее как Z=f(x).Естественно, в модели должно четко обозначаться направление желательного изменения Z – максимизация либо минимизация.
Наконец, совокупность внешних факторов мы обозначим как систему ограничений, которая может включать равенства и неравенства. Число таких факторов условимся обозначать m, а каждое отдельное ограничение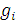 
(x).
Таким образом, имеем
( 
.
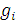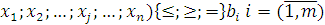В данном выражении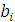 
обозначают численное значение ограничивающего фактора.
Итак, в структуре оптимизационной модели должны быть представлены три элемента: 1) вектор инструментальных переменных; 2) целевая функция; 3) система ограничений.
К определению вида модели имеют отношение следующие критерии:
1) характеристики управляемого объекта: более абстрактные (производство, распределение ресурсов или заданий) или более определенные ( запасы, потоки заявок на обслуживание);
2) характеристики значений переменных модели: случайные или строго определенные;
3) характеристики функций, описывающих модель: линейные или нелинейные;
4) подход к поиску оптимального решения: путем последовательных итераций; по шагам; с учетом возможной реакции оппонента и т.п.
По первому критерию выделяют типы моделей, разработанных для четко определенных специальных сфер принятия решений: модели управления запасами, модели систем массового обслуживания.
По второму критерию различают детерминированные и недетерминированные модели. Если ни одна из переменных модели не может принимать случайных значений, то модель является детерминированной, в противном случае – недетерминированной. В группе детерминированных моделей выделяют с применением третьего критерия модели линейного программирования и модели нелинейного программирования, а с применением четвертого критерия – модели динамического программирования. Отдельные модели управления запасами также являются детерминированными. Недетерминированные модели можно подразделить на модели с неопределенностью и вероятностные (стохастические) модели. В моделях с неопределенностью вероятность наступления того или иного значения переменной величины не поддается оценке. Такая особенность присуща некоторым видам математических игр. Стохастическими можно признать модели систем массового обслуживания, основную часть моделей управления запасами, некоторые математические игры.
На основе четвертого критерия можно различать: модели с итерационным способом приближения к оптимуму (модели линейного программирования); модели с пошаговым способом выбора оптимума (модели динамического программирования); модели, основанные на учете ответной реакции оппонента (математические игры).
Очевидно, что перечисленные критерии базируются на различных логических основаниях. К сожалению, научное сообщество пока не приняло единой основы классификации оптимизационных моделей. В данном пособии изложение основано на использовании принципа перехода от рассмотрения детерминированных моделей ( разделы 2-4) как более простых и абстрактных к моделям недетерминированным ( разделы 5-7). Вместе с тем неоднородность существующего классификационного подхода вынуждает отступать от данного принципа в некоторых частных моментах.
Раздел 2.
Линейное программирование
1.
2.
Дата добавления: 2018-05-02; просмотров: 1139; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!