Ускорение точки при движении по окружности

Предмет физики. Связь физики с другими науками. Границы применимости классической Мир, окружающий нас, материален: он состоит из вечно существующей и непрерывно движущейся материи. Материей в широком смысле слова называется все, что реально существует в природе (Вселенной) и может быть обнаружено человеком посредством органов чувств или с помошью специальных приборов. Например, процессы жизнедеятельности организмов, изучаемые биологией, всегда сопровождаются механическими, электрическими, внутриатомными и другими физическими процессами (но, конечно, не сводятся к этим процессам). Таким образом, можно сказать, что предмет исследования физики составляют общие закономерности явлений природы. Этим, однако, не исчерпывается связь физики с другими науками. Физика позволяет создавать приборы и вырабатывать методы исследования, необходимые для успешного развития всех естественных и прикладных наук. Трудно переоценить значение, которое имели, например, микроскоп в развитии биологии, телескоп — в астрономии, спектральный анализ — в химии, рентгеновский анализ — в медицине и т. п. Все естественные и прикладные науки широко и плодотворно применяют теперь метод меченых атомов, электронную аппаратуру и другие физические приборы и методы исследования. Кинематика материальной точки. Скорость и ускорение произвольно движущейся материальной точки. Кинема́тика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение. Движение любого объекта в кинематике изучают по отношению к некоторой системе отсчета, включающей: Тело отсчета; Систему измерения положения тела в пространстве (систему координат); Прибор для измерения времени (Часы).Материальная точка — тело, размерами которого по сравнению с характерными расстояниями данной задачи можно пренебречь. Ско́рость (часто обозначается , от англ. velocity или фр. vitesse) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора этой точки: Здесь — модуль скорости, — направленный вдоль скорости единичный вектор касательной к траектории в точке . Ускоре́ние (обычно обозначается , в теоретической механике ) — производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления). Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени: .

Ускорение точки при прямолинейном движении

Если вектор 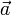не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:

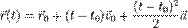Ускорение точки при движении по окружности

Вектор ускорения

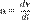при движении точки по окружности можно разложить на два слагаемых (компоненты):

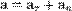Тангенциальное ускорение — 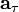направлено по касательной к траектории (обозначается иногда 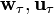и т.д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.

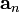Центростремительное или Нормальное ускорение — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда 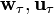итд). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:

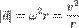Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:

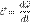Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.

3. Кинематика вращательного движения материальной точки.

Если в процессе движения абсолютно твердого тела (рис.2.1) его точки А и В остаются неподвижными, то и любая точка С тела, находящаяся на прямой АВ, также должна оставаться неподвижной. В противном случае расстояния АС и ВС должны были бы изменяться, что противоречило бы предположению об абсолютной твердости тела. Поэтому движение твердого тела, при котором две его точки Аи В остаются неподвижными, называют вращением тела вокруг неподвижной оси, а неподвижную прямую АВ называют осью вращения.

Рассмотрим произвольную точку М тела, не лежащую на оси вращения АВ. При вращении твердого тела расстояния М А и МВ и расстояние ρ точки М до оси вращения должны оставаться неизменными. Таким образом, все точки тела, вращающегося вокруг неподвижной оси, описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны этой оси. Движение абсолютно твердого тела, закрепленного в одной неподвижной точке, называют вращением тела вокруг неподвижной точки - центра вращения. Такое движение абсолютно твердого тела в каждый момент времени можно рассматривать как вращение вокруг некоторой оси, проходящей через центр вращения и называемой мгновенной осью вращения тела. Положение мгновенной оси относительно неподвижной системы отсчета и самого тела с течением времени может изменяться.

4. Динамика материальной точки. Законы Ньютона.

Теперь приступим к изучению следующего раздела механики - динамики, которая изучает движение материальных тел под действием приложенных к ним сил. Классическая динамика базируется на 3 основных законах, называемых законами Ньютона. Приведем формулировки этих законов, данные самим Ньютоном, в переводе академика А.Н. Крылова.

Закон 1. Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного прямолинейного движения, пока оно не понуждается приложенными силами изменить это состояние.

Закон 2. Изменение количества движения пропорционально приложенной силе и происходит по направлению прямой, по которой эта сила действует.

Закон 3. Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг с другом равны и направлены в противоположные стороны.

Первый закон называют законом инерции. Изолированная материальная точка, не взаимодействующая с другими материальными объектами, находится в состоянии покоя или равномерного прямолинейного движения. Это свойство тел сохранять свое первоначальное состояние называют инерцией. Мы из жизненного опыта знакомы со свойством инерции покоя тела, но в реальных условиях трудно наблюдать проявление свойства инерции равномерного движения тела, т.к. невозможно изолировать тело от взаимодействия с другими телами. Для этого необходимо абстрактно представить такие условия, когда отсутствуют внешние воздействия на движущееся тело. Только такая система отсчета, в которой закон инерции соблюдается, называется инерциальной системой отсчета. Инерциальная система отсчета связана с эвклидовым пространством, т.к. только в однородном и изотропном пространстве и в силу однородности времени переход материальной точки из одной точки в момент времени в точку 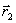в момент времени 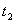не изменяет характеристики движения тела, в частности, и его скорость.

Очевидно, что понятие инерциальной системы является идеализацией, абстрактной моделью реальности. Возможность замены той или иной реальной системы этой моделью - инерциальной системой - определяется величиной взаимодействий и степенью точности измерений.

Второй закон является основой классической механики. Поскольку количество движения, определенное Ньютоном, как произведение массы тела на его скорость, т.е. 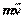, то математическая формулировка закона выражается формулой:

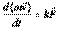. (2.1)В области нерелятивистских скоростей масса тела является величиной постоянной, поэтому имеем

, (2.2) или используя определение ускорения, имеем 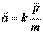. (2.3)В средней школе формулировку второго закона Ньютона дают в соответствии с формулой (2.3). Ускорение движения материальной точки совпадает по направлению с приложенной к ней силой, по модулю пропорционально модулю силы и обратно пропорционально массе материальной точки. Если все величины взять в международной системе единиц СИ, то второй закон Ньютона выразится векторным уравнением:

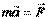(2.4)На основе этой формулы определяют единицу измерения силы в системе единиц СИ – ньютон, равный .На основе выражения (2.4) заключаем, что сила является причиной ускорения движения тела. При отсутствии действующей силы ускорение равно нулю 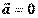и тело движется равномерно с постоянной скоростью 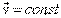или покоится . Таким образом, в качестве математического следствия из второго закона следует закон инерции, сформулированный первым законом Ньютона.

Из (2.3) следует, что с увеличением массы при неизменной силе ускорение уменьшается, а, следовательно, и изменение скорости движения уменьшается, т.е. инертность тела увеличивается. Отсюда выводится заключение, что масса является мерой инертности тела.

Изучение природы сил не входит в задачу классической механики, она определяется в других разделах физики. Классическая механика исходит из механической концепции взаимодействий тел, действующих между телами. Простым примером механической силыявляется взаимодействие двух тел при непосредственном соприкосновении их, происходящих при их столкновении, т.е. при ударе друг о друге. В природе наблюдается и другие примеры взаимодействия тел, находящихся на некотором расстоянии друг от друга, примером служит взаимодействие Земли и Солнца. В этом случае вводится понятие силового поля, которое производит взаимодействие тел, находящихся на расстоянии, при чем это взаимодействие распространяющихся мгновенно (представление дальнодействия Ньютона). Силовое поле задается в каждой точке пространства силой, которая может зависеть от времени . Это силовое поле не материальный объект, а вспомогательное математическое понятие. В механике считают, что взаимодействуют материальные точки через пустоту без помощи никакого-либо переносчика взаимодействия. Такое механическое рассмотрение распространяется на силы гравитационных взаимодействий и сил электромагнитных взаимодействий. К механическим силам так же относят и силы упругости, трения исопротивления среды, действующие на материальные тела.

При таком общем рассмотрении второй закон Ньютона записывают в виде

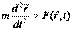, (2.5)дифференциального уравнения второго порядка, которое при задании определенных начальных условий описывает конкретное механическое явление. Поэтому этот закон именуют как основной закон механики.

Третий закон Ньютона, или закон равенства действия и противодействия, удобно формулировать следующим образом: силы, с которыми две материальные точки действуют друг на друга, расположены по прямой, соединяющей эти точки, равны по модулю и противоположны по направлению. Эти силы являются центральными. Для центральной силы линия силы всегда проходит через центр – точку, в котором находится источник силы. Обозначая вектор силы, с которой точка 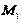действует на точку , через 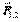, а силы, с которой точка 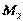действует на точку 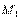, через 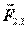, по третьему закону Ньютона имеем:

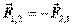. (2.6)

Необходимо отметить, что эти силы приложены к разным телам, и нельзя говорить о равнодействующей этих сил.

Закон сохранения импульса в классической механике.

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

Рассмотрим выражение определения силы

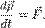
Перепишем его для системы из N частиц:

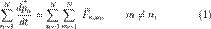
где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона, силы вида 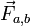и будут равны по абсолютному значению и противоположны по направлению, то есть 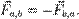Тогда после подстановки полученного результата в выражение (1) правая часть будет равна нулю, то есть:

или

Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит: 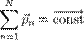(постоянный вектор).

То есть суммарный импульс системы частиц есть величина постоянная. Нетрудно получить аналогичное выражение для одной частицы.

Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы.

Также стоит подчеркнуть, что изменение импульса зависит не только от действующей на тело силы, но и от продолжительности её действия.

Инерциальные системы отсчета. Принцип относительности Галилея.

При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы винерциальных системах отсчёта

протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

Отсюда следует, что все законы природы одинаковы во всех инерциальных системах отсчёта.[1]

Различают принцип относительности Эйнштейна (который приведён выше) и принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов классической механики, подразумевая применимость преобразований Галилея, оставляя открытым вопрос о применимости принципа относительности к оптике и электродинамике.

Математически Г. п. о. выражает инвариантность (неизменность) уравнений механики относительно преобразований координат движущихся точек (и времени) при переходе от одной инерциальной системы к другой — преобразований Галилея.

Пусть имеются две инерциальные системы отсчёта, одну из которых, Σ, условимся считать покоящейся; вторая система, Σ', движется по отношению к Σ с постоянной скоростью u так, как показано на рисунке. Тогда преобразования Галилея для координат материальной точки в системах Σ и Σ' будут иметь вид:

x' = x - ut, у' = у, z' = z, t' = t (1)

(штрихованные величины относятся к системе Σ', нештрихованные — к Σ). Т. о., время в классической механике, как и расстояние между любыми фиксированными точками, считается одинаковым во всех системах отсчёта.

Из преобразований Галилея можно получить соотношения между скоростями движения точки и её ускорениями в обеих системах:

v' = v - u, (2)

a' = a.

В классической механике движение материальной точки определяется вторым законом Ньютона:

F = ma, (3)

где m — масса точки, a F — равнодействующая всех приложенных к ней сил. При этом силы (и массы) являются в классической механике инвариантами, т. е. величинами, не изменяющимися при переходе от одной системы отсчёта к другой. Поэтому при преобразованиях Галилея уравнение (3) не меняется. Это и есть математическое выражение Г. п. о.

Г. п. о. справедлив лишь в классической механике, в которой рассматриваются движения со скоростями, много меньшими скорости света. При скоростях, близких к скорости света, движение тел подчиняется законам релятивистской механики Эйнштейна (см.Относительности теория), которые инвариантны по отношению к другим преобразованиям координат и времени — Лоренца преобразованиям(при малых скоростях они переходят в преобразования Галилея).

Работа и кинетическая энергия.

Кинети́ческая эне́ргия — энергиямеханической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Единица измерения в системе СИ — Джоуль.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленнаядвижением.

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

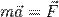
— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы 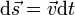. Учитывая, что 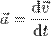, Получим:

Если система замкнута, то есть 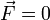, то 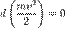, а величина

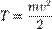
остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины и направления силы(сил) и от перемещения точки(точек) тела или системы.[1]. Работа силы (сил) над одной точкой

Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше в этом параграфе будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения[3]:

Потенциальное поле сил. Силы консервативные и неконсервативные.

Введем определение: стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называется потенциальным, а сами силы - консервативными.

Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными. К числу таких сил принадлежит, например, сила трения, так как работа этой силы зависит в общем случае от пути.

Покажем, что в потенциальном поле работа сил поля на любом замкнутом пути равна нулю. Действительно, любой замкнутый путь (рис. 5.5) можно разбить произвольно на две части: 1а2 и 2b1.

Потенциальная энергия. Примеры. Закон сохранения энергии в механике.

Сила называется потенциальной, если существует скалярная функция, известная как потенциальная энергия и обозначаемая Ep, такая что

Если все силы, действующие на частицу консервативны, и Ep является полной потенциальной энергий, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:

Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы

является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированнойфизической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии. Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.

Связь между потенциальной энергий и силой.

Для установления этой связи вычислим элементарную работу 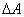, совершаемую силами поля при малом перемещении 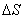тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой 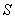. Эта работа равна

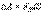где 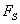- проекция силы 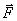на направление 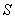.Поскольку в данном случае работа совершается за счет запаса потенциальной энергии 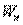, она равна убыли потенциальной энергии 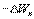на отрезке оси :

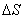Из двух последних выражений получаем 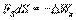Откуда 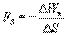Последнее выражение дает среднее значение 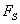на отрезке 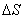. Чтобыполучить значение 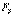в точке нужно произвести предельный переход: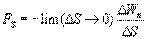

Так как может изменяться не только при перемещении вдоль оси 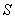, но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от 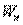по :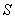

Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:

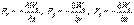Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:

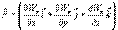в математике вектор 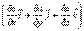,где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом 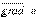.Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком

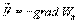
Движение твердого тела. Закон вращения твердого тела вокруг неподвижной оси.

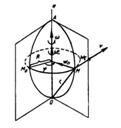Вращением вокруг неподвижной оси называется такое движение твердого тела, при котором во все время движения две его точки остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на оси вращения. Положение вращающегося твердого тела определяется одним параметром - углом φ между начальным положением АМ0О некоторой плоскости, связанной с телом и проходящей через ось, и ее положением АМО в данный момент времени (рис. 1).

Рисунок 1.

Закон вращательного движения: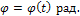

Проекция вектора угловой скорости на ось и определяется зависимостью: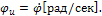

Угловая скорость ω рад/сек связана с числом оборотов в минуту n зависимостями: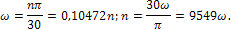

Проекция вектора угловой скорости на ось u определяется зависимостью

Скорость и ускорение точки М вращающегося твердого тела определяются соотношениями (рис. 1):

или в скалярной форме:

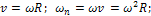
Частные случаи:

1) равномерное вращение (ε=0):

2) равнопеременное вращение (εu=const):

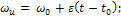
Момент импульса твердого тела. Закон сохранения момента импульса.

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.

Закон сохранения момента импульса есть проявление изотропности пространства.

Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.
Это один из фундаментальных законов природы.
Аналогично для замкнутой системы тел, вращающихся вокруг оси z: 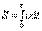отсюда 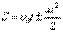или .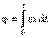

Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения.
Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.
Очень нагляден закон сохранения момента импульса в опытах с уравновешенным гироскопом – быстро вращающимся телом, имеющим три степени свободы

Кинетическая энергия вращающегося тела. Работа сил при вращении тела вокруг неподвижной оси.

Кинетическая энергия – величина аддитивная. Поэтому кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек, на которые это тело можно мысленно разбить: 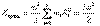, (6.4.1)

Если тело вращается вокруг неподвижной оси z с угловой скоростью 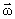, то линейная скорость i-й точки , Ri – расстояние до оси вращения. Следовательно, , (6.4.2)

Сопоставив (6.4.1) и (6.4.2), можно увидеть, что момент инерции тела I является мерой инертности при вращательном движении, так же как масса m – мера инерции при поступательном движении.
В общем случае движение твердого тела можно представить в виде суммы двух движений – поступательного со скоростью vc и вращательного с угловой скоростью ω вокруг мгновенной оси, проходящей через центр инерции. Тогда полная кинетическая энергия этого тела , (6.4.3)

Здесь Ic – момент инерции относительно мгновенной оси вращения, проходящей через центр инерции.

Моменты инерции некоторых тел. Свободные оси.

Момент инерции — скалярнаяфизическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Для того чтобы сохранить положение оси вращения твердого тела с течением времени неизменным, используют подшипники, в которых она удерживается. Однако существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения). Можно доказать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела).

Теорема Штейнера.

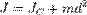где JC — известный момент инерции относительно оси, проходящей через центр масс тела,

J — искомый момент инерции относительно параллельной оси, m — масса тела, d — расстояние между указанными осями.

Момент инерции, по определению: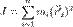

Радиус-вектор можно расписать как разность двух векторов: ,

где — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид: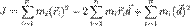

Вынося за сумму , получим:

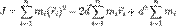
Так как старая ось проходит через центр масс, то по определению центра масс. Тогда

Откуда и следует искомая формула: ,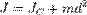

где JC — известный момент инерции относительно оси, проходящей через центр масс тела.

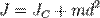
Основные представления молекулярно-кинетической теории. Масса и размеры молекул. Понятие о статистическом методе.

Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ.

В основе молекулярно-кинетической теории лежат три основных положения:

Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными, т.е. состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

Атомы и молекулы находятся в непрерывном хаотическом движении.

Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Наиболее ярким экспериментальным подтверждением представлений молекулярно-кинетической теории о беспорядочном движении атомов и молекул является броуновское движение. Это тепловое движение мельчайших микроскопических частиц, взвешенных в жидкости или газе. Оно было открыто английским ботаником Р. Броуном в 1827 г. Броуновские частицы движутся под влиянием беспорядочных ударов молекул. Из-за хаотического теплового движения молекул эти удары никогда не уравновешивают друг друга. В результате скорость броуновской частицы беспорядочно меняется по модулю и направлению, а ее траектория представляет собой сложную зигзагообразную кривую . Теория броуновского движения была создана А. Эйнштейном в 1905 г. Экспериментально теория Эйнштейна была подтверждена в опытах французского физика Ж. Перрена, проведенных в 1908–1911 гг.

Атомная единица массы (а.е.м.) - 1,6.10-27кг - единица массы, равная 1/12 массы изотопа углерода с массовым числом 12.

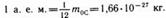, где m0 - масса молекулы (атома); m0С - масса атома углерода (изотоп 12С) - относительная атомная масса - определяется по таблице Менделеева!

Относительная молекулярная масса сложного вещества определяется как сумма относительных атомных масс всех атомов, входящих в состав данного вещества.

Опытные газовые законы. Уравнение Менделеева-Клапейрона.

Уравнение состоянияидеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температуройидеального газа. Уравнение имеет вид:

где 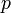— давление, 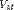— молярный объём, 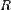— универсальная газовая постоянная 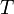— абсолютная температура,К.

Так как 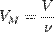, где 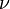— количество вещества, а , где 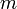— масса, 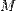— молярная масса, уравнение состояния можно записать:

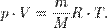Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде: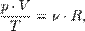

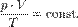
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

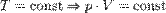— закон Бойля — Мариотта. 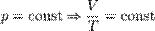— Закон Гей-Люссака.

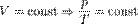— закон Шарля (второй закон Гей-Люссака, 1808 г.)

Основное уравнение молекулярно-кинетической теории газ зов и его следствия.

Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура).

В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.

Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона.

Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

Внутренняя энергия газа. Число степеней свободы молекулы.

Внутренняя энергия — это кинетическая энергия хаотического (теплового) движения частиц системы (молекул, атомов, ядер, электронов) и потенциальная энергия взаимодействия этих частиц.
Внутренняя энергия идеального газа есть сумма кинетических энергий его частиц (энергией взаимодействия частиц пренебрегаем).

Число степеней свободы — это число независимых переменных, полностью определяющих положение молекулы как системы атомов в пространстве.

Газ		одноатомный	двухатомный	трехатомный
Число степеней свободы	поступательных	3	3	3
	вращательных	—	2	3
	всего	3	5	6

Закон Больцмана о равномерном распределении энергии по степеням свободы молекулы:
На каждую степень свободы молекулы приходится в среднем одинаковая энергия
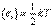, где
— постоянная Больцмана, 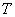— абсолютная температура газа.

Таким образом, средняя кинетическая энергия одной молекулы газа , где
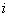— сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы.
.
На колебательную степень свободы приходится вдвое большая энергия потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы.

Внутренняя энергия газа, содержащего 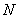частиц, количеством 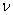молей и массой :
.

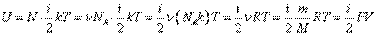Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам. Уравнение Майера.

Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии длятермодинамических систем.

Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, английского физика Дж. П. Джоуля и немецкого физика Г. Гельмгольца[1]. Согласно первому началу термодинамики, термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника.

Рассмотрим несколько частных случаев:

Если δQ > 0, то это означает, что тепло к системе подводится.

Если δQ < 0, аналогично — тепло отводится.

Если δQ = 0, то система не обменивается теплом с окружающей средой и называется адиабатически изолированной.

Обобщая: в конечном процессе 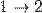элементарные количества теплоты могут быть любого знака. Общее количество теплоты, которое мы назвали просто Q — это алгебраическая сумма количеств теплоты, сообщаемых на всех участках этого процесса. В ходе процесса теплота может поступать в систему или уходить из неё разными способами.

При отсутствии работы над системой и потоков энергии-вещества, когда δA' = 0, δQ = 0, dN = 0, выполнение системой работы δA приводит к тому, что ΔU < 0, и энергия системы U убывает. Поскольку запас внутренней энергии U ограничен, то процесс, в котором система бесконечно долгое время выполняет работу без подвода энергии извне, невозможен, что запрещает существование вечных двигателей первого рода.

Первое начало термодинамики:при изобарном процессе

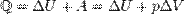при изохорном процессе (A = 0)

при изотермическом процессе (ΔU = 0)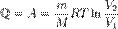

Здесь 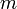— масса газа, — молярная масса газа, — молярная теплоёмкость при постоянном объёме, 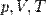— давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.

Cp = Cv + R
Оно показывает, что расширение моля идеального газа при постоянном давлении и изменении его температуры на 1 Кельвин требует дополнительного, по сравнению с изобарическим расширением, количества теплоты, необходимого для совершения работы. Это значение равно универсальной газовой постоянной....;)

Теплоемкость идеального газа. Физический смысл универсальной газовой постоянной.

Теплоемкость идеального газа — это отношение тепла, сообщенного газу, к изменению температуры δТ, которое при этом произошло.

Молярная теплоемкость — теплоемкость 1 моля идеального газа.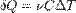

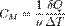
В уравнение состояния идеального газа (уравнение Менделеева — Клапейрона) .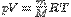

входит универсальная газовая постоянная R. Она, как известно, равна произведению двух других постоянных — числа Авогадро NA и постоянной Больцмана k: .

Постоянные NA и k имеют ясный смысл: NA — это число молекул или атомов в единице количества вещества, то есть моле; k — постоянная, определяющая связь между температурой в Кельвинах и температурой в единицах энергии. Но определенные физический смысл (быть может, многим он покажется неожиданным) имеет и комбинация NA и k — постоянная R.

Представим себе, что 1 моль идеального газа находится в сосуде с подвижным поршнем и что подводом тепла к нему или отводом тепла от него его температуру изменяют на 1 кельвин. Благодаря тому, что сосуд закрыт подвижным поршнем, давление газа будет оставаться постоянным (нравным внешнему давлению).

Напишем уравнение состояния газа до и после нагревания:до нагревания ,после нагревания 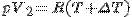, где ΔT = 1 К.

Вычтя первое равенство из второго, мы получим .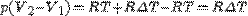

Левая часть этого равенства представляет собой работу, совершаемую силой давления газа (или внешней силой против силы давления), когда при постоянном давлении р объем газа увеличивается (или уменьшается) от V1 до V2. Следовательно, газовая постоянная R равна работе, которую совершает 1 моль идеального газа, расширяясь при нагревании на 1 К при постоянном давлении.

Разумеется, при изобарном охлаждении 1 моля газа на 1 К такую же работу совершает внешняя сила, действующая на поршень.

22. Процессы с газами. Работа газа при различных процессах.

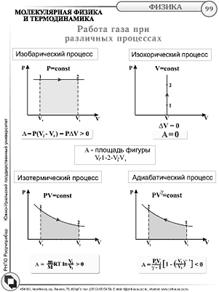Адиабатический процесс. Уравнение адиабаты.

Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии. Серьёзное исследование адиабатических процессов началось с XVIII века[1].

Основное уравнение термодинамики для адиабатического процесса

Для адиабатического процесса первое начало термодинамики в силу отсутствия теплообмена (ΔQ = 0) системы со средой имеет вид[4][5]

,где: — изменение внутренней энергии тела, 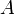— работа, совершаемая системой

— теплота, полученная системой

Основное уравнение термодинамики применительно к адиабатическому процессу записывается в дифференциалах как ,

где 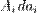— дифференциальное выражение для работы, ai — внешние параметры, Ai — соответствующие им внутренние параметры.

Энтропия системы в обратимом адиабатическом процессе не меняется[6]: .

Круговые процессы (циклы). Тепловые и холодильные машины. К.п.д. тепловой машины.

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно .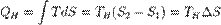

Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику .

Отсюда коэффициент полезного действия тепловой машины Карно равен .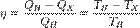

Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины, будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Например, КПД идеального цикла Стирлинга равен КПД цикла Карно.

Цикл Карно. К.п.д. идеальной тепловой машины.

Пусть тепловая машина состоит из нагревателя с температурой TH, холодильника с температурой TX и рабочего тела.

Цикл Карно состоит из четырёх стадий:

Изотермическое расширение (на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуру TH, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты QH. При этом объём рабочего тела увеличивается.

Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

Изотермическое сжатие (на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуру TX, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты QX.

Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия:

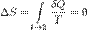при δQ = 0.Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия).

Энтропия. Второе начало термодинамики.

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не должна равняться 0.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Энтропи́я (от греч. ἐντροπία — поворот, превращение) в естественных науках — мера порядка системы, состоящей из единого элемента. В частности, встатистической физике — меравероятности осуществления конкретного макроскопического состояния; в теории информации — мера конкретизации какого-либо опыта (испытания), который должен иметь разные исходы, а значит и качество информации; в исторической науке, для экспликациифеноменаальтернативности истории (инвариантности и вариативности исторического процесса).

Статистический смысл второго начала термодинамики. Энтропия и вероятность.

Число столкновений и длина свободного пробега молекул в газе.

Средние скорости молекул, газа очень велики - порядка сотен метров в секунду при обычных условиях. Однако процесс выравнивая неоднородности в газе вследствие молекулярного движения протекает весьма медленно. Это объясняется тем, что молекулы при перемещении испытывают соударения с другими молекулами. При каждом соударении скорость молекулы изменяется по величине и направлению. Вследствие этого, скорость, с которой молекула диффундирует из одной части газа в другую, значительно меньше средней скорости молекулярного движения. Для оценки скорости движения молекул вводится понятие средней длины свободного пробега. Таким образом, средняя дли свободного пробега - это среднее расстояние, которое проходит молекула от столкновения до столкновения.

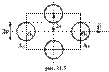Для определения вычислим сначала среднее число соударений 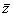выбранной молекулы с другими молекулами за единицу времени. Будем считать, что молекула после соударения продолжает двигаться по прямой со средней скоростью движения .

Молекулы, с которыми соударяется выбранная молекула, в первом приближении считаем неподвижными и принимаем их за сферические тела радиуса r. Пусть выбранная молекула движется вправо из положения 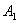в положение 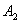по прямой 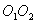(рис.11.3). При своем движении она испытывает соударения с теми неподвижными молекулами, центры которых лежат не дальше чем 2r от траектории 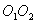. Иными словами, движущаяся со средней скоростью молекула в течении одной секунды столкнется со всеми молекулами, центры которых находятся в объеме ограниченном цилиндром с радиусом 2r и длиной , т.е. .

Если концентрация молекул n , то внутри рассмотренного цилиндра находится число молекул, равное

Это число 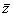и определяет среднее число соударений за единицу времени.

Предположение о том, что все молекулы, кроме одной, неподвижны, является, конечно не верным. В действительности все молекулы движутся, и возможность соударения двух частиц зависит от их относительной скорости. Поэтому вместо среднеарифметической скорости должны входить средняя относительная скорость молекул . Если скорости молекул распределены по закону Максвелла, то, как можно показать, средняя относительная скорость двух молекул однородного газа в раз превышает . Таким образом, среднее число соударений должно быть увеличено в раз

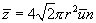(11.7)Средний путь, проходимый молекулой за единицу времени, численно равен . Поэтому средняя длина свободного пробега равна или 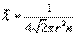(11.8)

Таким образом, средняя длина свободного пробега не зависит от температуры газа, т.к. с ростом температуры одновременно возрастают 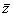и , и . При подсчете числа соударений и средней длины свободного пробега молекул за модель молекулы было принято шарообразное упругое тело. В действительности каждая молекула представляет собой сложную систему элементарных частиц и при рассмотрении упругого соударения молекул имелось в виду, что центры молекул могут сблизиться до некоторого наименьшего расстояния. Затем возникает силы отталкивания которые вызывают взаимодействие, подобное взаимодействию при упругом ударе. Среднее расстояние между центрами молекул, взаимодействующих, как при упругом ударе, называют эффективным диаметром 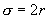. Тогда (11.9)

Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы реального газа.

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:

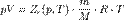где p — давление; V - объем T — температура; Zr = Zr (p,T) — коэффициент сжимаемости газа; m - масса; М —молярная масса; R — газовая постоянная.

Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

где

V — объём,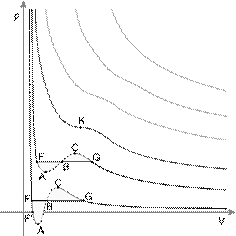

Изотермыреального газа (схематично)

Синие — изотермы при температуре ниже критической. Зелёные участки на них — метастабильные состояния.

Участок левее точки F — нормальная жидкость.
Точка F — точка кипения.
Прямая FG — равновесие жидкой и газообразной фазы.
Участок FA — перегретая жидкость.
Участок F′A — растянутая жидкость (p<0).
Участок AC — аналитическое продолжение изотермы, физически невозможен.
Участок CG — переохлаждённый пар.
Точка G — точка росы.
Участок правее точки G — нормальный газ.
Площади фигуры FAB и GCB равны.

Красная — критическая изотерма.
K — критическая точка.

Голубые — сверхкритические изотермы

Свойства электрического заряда. Закон Кулона. Закон сохранения электрического заряда. Работа по перемещению заряда в электростатическом поле.

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Электрический заряд обычно обозначается буквами q или Q.Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:Существует два рода электрических зарядов, условно названных положительными и отрицательными.

Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. На основании многочисленных опытов Кулон установил следующий закон:

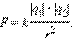Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда.

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:q1 + q2 + q3 + ... +qn = const.

Коэффициент k в системе СИ обычно записывают в виде: где 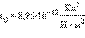– электрическая постоянная.

В системе СИ элементарный заряд e равен:e = 1,602177·10–19 Кл ≈ 1,6·10–19 Кл.При перемещении пробного заряда q в электрическом поле электрическиесилы совершают работу. Эта работа при малом перемещении 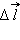равна (рис. 1.4.1):

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Электрическое поле. Напряженность

Электрическое поле — одна из составляющих электромагнитного поля; особый вид материи, существующий вокруг тел или частиц, обладающихэлектрическим зарядом, а также в свободном виде при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может наблюдаться благодаря его силовому воздействию на заряженные тела. Электрическое поле обладает энергией. Плотность этой энергии определяется величиной поля и может быть найдена по формуле

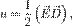где E — напряжённость электрического поля, D — индукция электрического поля.

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношениюсилы действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q: .

Теорема Остроградского-Гаусса для поля в вакууме.

Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. 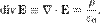Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона (см. ниже). Формула однако также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте ее логичнее называть законом Гаусса[2].

Примеры применения теоремы Остроградского Гаусса.

Являясь (вкупе с уравнением о нулевой циркуляции электрического поля) основным полевым уравнением электростатики (вместе эти два уравнения в диффененциальной форме эквивалентны уравнению Пуассона — основному и единственному дифференциальному уравнению классической теории для электростатического потенциала.

В электродинамике теорема Гаусса (закон Гаусса) также остается (полностью в том же виде) одним из главных уравнений — одним из четырех уравнений Максвелла.

В некоторых ситуациях теорема Гаусса может быть использована для прямого и легкого вычисления электростатического поля непосредственно. Это ситуации, когда симметрия задачи позволяет наложить на напряженность электрического поля такие дополнительные условия, что вместе с теоремой Гаусса этого хватает для прямого элементарного вычисления (без применения двух обычных общих способов — решения уравнения в частных производных или лобового интегрирования кулоновских полей для элементарных точечных зарядов).

Именно таким способом с использованием теоремы Гаусса может быть выведен и сам закон Кулона (см. выше).

Конкретные примеры такого применения теоремы Гаусса разобраны здесь ниже.В них используются следующие величины и обозначения:Объёмная плотность заряда 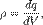где dV — (бесконечно малый) элемент объема,

Поверхностная плотность заряда 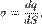где dS — (бесконечно малый) элемент поверхности.

Линейная плотность заряда

где dl — длина бесконечно малого отрезка. (Первая используется для зарядов, непрерывно распределенных по объему, вотрая — для распределенных по поверхности, третья — для распределенных по одномерной линии (кривой, прямой).

Потенциал электростатического поля.

Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда (для любой системы единиц; подробнее о единицах измерения — см. ниже). Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда: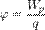

Напряжённость электростатического поля 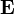и потенциал 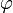связаны соотношением

или обратно

В СИ за единицу разности потенциалов принимают вольт (В). Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в одинкулон нужно совершить работу в один джоуль: 1В = 1 Дж/Кл (L²MT−3I−1).

Электрическое поле в веществе. Типы диэлектриков.

Диэлектриками называются вещества, которые в обычных условиях практически не проводят электрический ток, их удельное сопротивление в 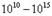раз больше, чем у металлов. Согласно представлениям классической физики, в диэлектриках, в отличие от проводников, нет свободных носителей заряда, которые могли бы под действием электрического поля создавать ток проводимости.

К диэлектрикам относятся все газы; некоторые жидкости (дистиллированная вода, масла, бензол); твердые тела (стекло, фарфор, слюда). Термины "диэлектрик" и "диэлектрическая постоянная" были введены в науку в 1837 г. M. Фарадеем. Если диэлектрик внести в электрическое поле, то это поле и сам диэлектрик претерпевают существенные изменения

Теорема Остроградского-Гаусса для поля в диэлектрике. Электрическое смещение.

В неоднородной диэлектрической среде 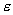имеет различные значения, изменяясь на границах диэлектриков скачкообразно (претерпевая разрыв). Это затрудняет применение формул, описывающих взаимодействие зарядов в вакууме. Что касается теоремы Гаусса, то в этих условиях она вообще теряет смысл. В самом деле, благодаря различной поляризуемости разнородных диэлектриков напряженности поля в них будут различными. Поэтому различно и число силовых линий в каждом диэлектрике (рис.14.6).

Часть линий, исходящих из зарядов, окруженных замкнутой поверхностью, будет заканчиваться на границе раздела диэлектриков и не пронижет данную поверхность. Это затруднение можно устранить, введя в рассмотрение новую физическую характеристику поля – вектор электрического смещения 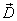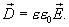(14.8)

Вектор 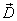направлен в ту же сторону, что и 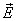. В отличие от напряженности поля 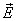вектор 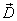имеет постоянное значение во всех диэлектриках. Поэтому электрическое поле в неоднородной диэлектрической среде удобнее характеризовать не напряженностью 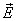, а смещением 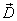. С этой целью вводится понятие линий вектора 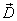и потока смещения, аналогично понятию силовых линий и потока напряженности

или 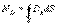(14.9)Используя теорему Гаусса 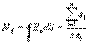домножим обе части на

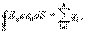
С учетом (14.8) получаем 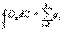(14.10)

Это уравнение выражает теорему Гаусса для вектора электрического смещения: полный поток вектора электрического смещения через произвольную замкнутую поверхность равен сумме свободных зарядов, заключенных в этой поверхности.

Проводники в электрическом поле.

Вещество или материальное тело, в котором имеются заряды, способные переносить электрический ток, называется проводником. В металлах переносчиками тока служат свободные (т.е. не привязанные к атомам) электроны, в электролитах — ионы, в плазме — и электроны, и ионы. Для электростатических явлений поле внутри проводника равно нулю:

E→in ≡ 0 .Механизм исчезновения электрического поля в проводниках связан со смещением свободных зарядов ровно настолько, чтобы как раз компенсировать внешнее электрическое поле, если таковое имеется. При изменении внешнего поля свободные заряды в проводнике перераспределяются, а в момент перераспределения в проводнике течет ток. Пример такой компенсации внутри проводящей пластины изображен на рис. 1.25.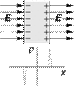

Проводящая пластина в однородном электрическом поле и распределение плотности заряда в объёме проводника. В плазме толщина заряженного слоя на поверхности составляет несколько радиусов Дебая, в металле — несколько длин Ферми.

Поскольку E→in = 0, то и плотность заряда внутри проводника также равна нулю:ρin = 1 4π divE→in ≡ 0.

Заряды, компенсирующие внешнее поле, могут размещаться только на поверхности проводника. В связи с этим говорят, что проводник квазинейтрален. По аналогии с объёмной плотностью заряда ρ = limΔV →0Δq∕ΔV , поверхностную плотность определяют, как предел отношения заряда на физически малом участке поверхности Δq к площади этого участка ΔS:σ = limΔS→0Δq∕ΔS .

Все точки проводника имеют одинаковый потенциал, так как gradϕin = −E→in = 0. Поверхность проводника также эквипотенциальна. Следовательно, электрическое поле перпендикулярно к ней. Этот факт иногда формулируют в виде равенства нулю тангенциальной (касательной к поверхности проводника) проекции внешнего электрического поля E→t =[[n→,E→],n→]:E→t = 0.

Здесь и далее n→ обозначает внешнюю нормаль к поверхности проводника.

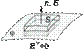
Поток через верхнюю грань параллелепипеда, натянутого на элемент поверхности S, равен En S; поток через остальные грани равен нулю. Сравнивая En S с полным зарядом 4πσ S внутри параллелепипеда, получаем граничное условие En = 4πσ.

Нормальная компонента электрического поля на поверхности проводника En = (n→,E→) однозначно связана с поверхностной плотностью зарядов. Применяя теорему Гаусса к параллелепипеду, натянутому на элемент поверхности проводника (рис. 1.26), получаем:E→n = 4πσ .

Обычно распределение зарядов σ по поверхности проводника неизвестно. Если нужно, его находят в результате решения задачи (см. след. параграф). Однако одну существенную закономерность можно указать из качественных соображений (Б.Франклин, 1747 г.). Так как одноименные заряды (заряды одного знака) отталкиваются, они стремятся разойтись в проводнике как можно дальше. Это приводит к накоплению зарядов на наиболее удаленных участках проводников, например на остриях. Поле вблизи острия можно приближенно представить, как поле заряженной сферы того же радиуса кривизны r. Отсюда можно оценить напряженность электрического поля и поверхностную плотность заряда 4πσ ∼ E ∼ ϕ∕r, гдеϕ — потенциал проводника относительно соседних тел. При этом полезно отметить, что полный заряд острия q ∼ πr2σ ∼ ϕr все-таки составляет малую долю заряда всего проводящего телаQ ∼ ϕR, где R — его характерный размер.

Электроемкость уединенного проводника. Конденсаторы.

Электроемкостью (емкостью) C уединенного изолированного проводника называется физическая величина, равная отношению изменения заряда проводника q к изменению его потенциала f:C = Dq/Df.

Электроемкость уединенного проводника зависит только от его формы и размеров, а также от окружающей его диэлектрической среды (e).

Единица измерения емкости в системе СИ называется Фарадой. Фарада (Ф) - это емкость такого уединенного проводника, потенциал которого повышается на 1 Вольт при сообщении ему заряда в 1 Кулон.
1 Ф = 1 Кл/1 В.

Конденсатором называют систему двух разноименно заряженных проводников, разделенных диэлектриком (например, воздухом).
Свойство конденсаторов накапливать и сохранять электрические заряды и связанное с ними электрическое поле характеризуется величиной, называемой электроемкостью конденсатора. Электроемкость конденсатора равна отношению заряда одной из пластин Q к напряжению между ними U:C = Q/U.

В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими и цилиндрическими. Формулы для расчета емкостей этих конденсаторов приведены в таблице.

Тип конденсатора	Схематическое изображение	Формула для расчета емкости	Примечания
Плоский конденсатор		C = ee0S/d	S - площадь пластины; d - расстояние между пластинами.
Сферический конденсатор		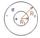C = 4pee0R1R2/(R2 - R1)	R2 и R1 - радиусы внешней и внутренней обкладок.
Цилиндрический конденсатор		C = 2pee0h/ln(R2/R1)	h - высота цилиндров.

Энергия заряженного проводника, конденсатора.

Если уединенный проводник имеет заряд q, то вокруг него существует электрическое поле, потенциал которого на поверхности проводника равен 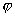, а емкость - С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная . Но потенциал электростатического поля данного проводника в бесконечности равен нулю 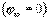. Тогда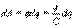

При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.

Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:

Применяя соотношение , можно получить следующие выражения для потенциальной энергии W: 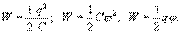(16.2)

Для заряженного конденсатора разность потенциалов (напряжение) равна поэтому соотношение для полной энергии его электростатического поля имеют вид

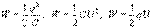(16.3)

Энергия электростатического поля.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую (рис. 1.7.1). При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов при переносе каждой порции Δq внешние силы должны совершить работу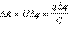

Энергия Wе конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q: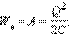

Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.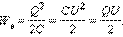

Электрическую энергию Wе следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для Wе аналогичны формулам для потенциальной энергии Eр деформированной пружины (см. ч. I, § 2.4) где k – жесткость пружины, x – деформация, F = kx – внешняя сила.

По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора.

Напряженность однородного поля в плоском конденсаторе равна E = U/d, а его емкость 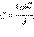Поэтому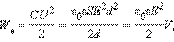

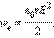где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина

является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.

Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.

Электрический ток, его характеристики и условия существования.

Электрический ток - упорядоченное по направлению движение электрических зарядов. За направление тока принимается направление движения положительных зарядов. Прохождение тока по проводнику сопровождается следующими его действиями:магнитным (наблюдается во всех проводниках) тепловым (наблюдается во всех проводниках, кроме сверхпроводников)химическим (наблюдается в электролитах).

УСЛОВИЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА

Для возникновения и поддержания тока в какой-либо среде необходимо выполнение двух условий:наличие в среде свободных электрических зарядов

создание в среде электрического поля.

В разных средах носителями электрического тока являются разные заряженные частицы.

Скорость хаотического движения электронов в металле.

Концентрация n атомов в металлах находится в пределах 1028–1029 м–3.

Оценка по этой формуле для металлического проводника сечением 1 мм2, по которому течет ток 10 А, дает для средней скорости 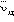упорядоченного движения электронов значение в пределах 0,6–6 мм/c. Таким образом, средняя скорость 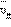упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости 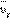их теплового движения 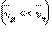Рис. 1.12.3 дает представление о характере движения свободного электрона в кристаллической решетке.

Рисунок 1.12.3.

Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа сильно преувеличены

Малая скорость дрейфа на противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·108 м/с. Через время порядка l / c (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.

Скорость направленного движения электронов в металле.

Смотри вопрос 46.

Закон Ома в дифференциальной и интегральной формах.

Закон Ома записывается формулой: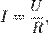

где: I — сила тока (А), U — напряжение (В), R — сопротивление (Ом).

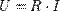Закон Ома для участка электрической цепи имеет вид: или или

где: — напряжение или разность потенциалов, — сила тока, 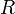— сопротивление.

Закон Ома также применяется ко всей цепи, но в несколько изменённой форме: ,

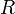где:ε — ЭДСисточника напряжения, — сила тока в цепи, — сопротивление всех внешних элементов цепи, — внутреннее сопротивлениеисточника напряжения.

Закон Ома в дифференциальной форме

Сопротивление 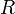зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем: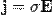

где: 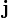— вектор плотности тока, 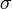— удельная проводимость, 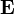— вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ленца-Джоуля в дифференциальной и интегральной формах.

Математически может быть выражен в следующей форме:

где w — мощность выделения тепла в единице объёма, 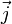— плотность электрического тока, 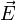— напряжённость электрического поля, σ — проводимость среды.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:

В математической форме этот закон имеет вид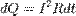

где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:

Закон Видемана-Франца.

Зако́н Видема́на — Фра́нца — это физический закон, утверждающий, что для металлов отношение коэффициента теплопроводности (либо тензора теплопроводности) K к удельной электрической проводимости (либо тензору проводимости) σ пропорционально температуре: .

Взаимная связь электрической проводимости и теплопроводности объясняется тем, что оба эти свойства металлов в основном обусловлены движением свободных электронов.

Коэффициент теплопроводности увеличивается пропорционально средней скорости частиц, так как ускоряется перенос энергии. Электропроводность, наоборот, падает, потому что соударения при большой скорости частиц значительно затрудняют перенос энергии .

Друде, применив классическую кинетическую теорию газов, получил значение коэффициента L: ,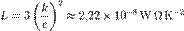

где k — постоянная Больцмана, e — заряд электрона.

В своем первоначальном расчете Друде ошибся в 2 раза, получив при этом правильный порядок величины. Фактически, классическая статистика дает результат ,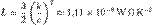

Только с помощью квантовой статистики Зоммерфельдом было получено значение коэффициента L, хорошо согласующееся с экспериментом: .

Закон Видемана-Франца стал триумфом теории свободных электронов.

Классическая электронная теория электропроводности металлов.

Исходя из представлений о свободных электронах, Друде разработал классическую теорию электропроводности металлов, которая затем была усовершенствована Лоренцем. Друде предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершено свободно, пробегая в среднем некоторый путь 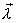. Правда в отличие от молекул газа , пробег которых определяется соударениями молекул друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой. Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, оценку средней скорости теплового движения электронов можно произвести по формуле 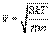. Для комнатной температуры ( 300К) вычисление по этой формуле приводит к следующему значению: 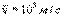. При включении поля на хаотическое тепловое движение, происходящее, со скоростью 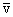, накладывается упорядоченное движение электронов с некоторой средней скоростью . Величину этой скорости легко оценить, исходя из формулы, связывающей плотность тока j с числом n носителей в единице объема, их зарядом е и средней скоростью : (18.1)

Предельная допустимая техническими нормами плотность тока для медных проводов составляет около 10 А/мм2 = 107 А/м2. Взяв для n=1029 м-3, получим

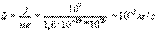Таким образом, даже при больших плотностях тока средняя скорость упорядоченного движения зарядов в 108 раз меньше средней скорости теплового движения .

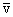Дата добавления: 2018-05-02; просмотров: 1012; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!