Двойственность в линейном программировании
Каждой задаче линейного программирования можно поставить в соответствие другую задачу линейного программирования, так называемую двойственную задачу.
Рассмотрим задачу об оптимальном выпуске продукции (12)-(13):
 (12)
(12)

 (13)
(13)
Каждому ограничению ставится в соответствие переменная двойственной задачи 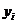 . Двойственная задача имеет вид:
. Двойственная задача имеет вид:
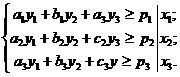 (18)
(18)
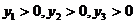
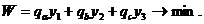 (19)
(19)
Для составления модели двойственной задачи необходимо учесть следующие свойства:
1.Число ограничений исходной задачи равно числу неизвестных двойственной.
2. Матрица коэффициентов при неизвестных одной задачи транспонируется для неизвестных другой задачи.
3. Знаки в неравенствах исходной задачи и двойственной имеют противоположный смысл, в исходной знак “ 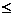 ”, в двойственной знак “
”, в двойственной знак “  ”.
”.
4. Свободные члены ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи, коэффициенты целевой функции исходной задачи ─ свободными членами неравенств двойственной задачи.
5. В исходной задаче целевая функция  , в двойственной задаче
, в двойственной задаче 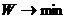 .
.
|
|
|
Задачи (12)–(13) и (18)–(19) называются симметричными взаимно двойственными задачами. Модель двойственной задачи к исходной (14) – (15) имеет вид:
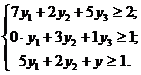
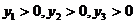

Если одну из задач решить симплексным методом, то неизвестные в двойственной задаче равны соответствующим оптимальным оценкам базисных переменных исходной задачи плюс коэффициент (  ), стоящий в таблице над соответствующей базисной переменной.
), стоящий в таблице над соответствующей базисной переменной.
 ,
,  ,
, 
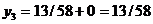 .
.
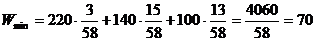 .
.
Задание 7. Транспортная задача
В пунктах производства 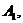
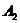 ,
,  ,
,  имеется однородный груз в количестве соответственно
имеется однородный груз в количестве соответственно 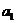 ,
, 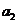 ,
, 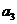 ,
,  . Данный груз необходимо доставить в 3 пункта назначения
. Данный груз необходимо доставить в 3 пункта назначения 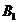 ,
,  ,
,  в количестве соответственно
в количестве соответственно 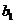 ,
, 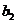 ,
, 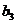 . Стоимость перевозки единицы груза (тариф) из пункта
. Стоимость перевозки единицы груза (тариф) из пункта 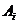 в пункт
в пункт 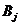 равна
равна  . Требуется составить план перевозок, при котором все грузы будут вывезены с минимальными затратами.
. Требуется составить план перевозок, при котором все грузы будут вывезены с минимальными затратами.
Таблица 8– Данные задания 7 «Транспортная задача»
| № | 
| 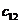
| 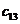
| 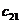
| 
| 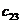
| 
| 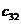
| 
| 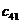
| 
| 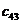
|
| 1 | 4 | 3 | 6 | 4 | 1 | 6 | 2 | 8 | 2 | 8 | 3 | 7 |
| 2 | 4 | 3 | 6 | 4 | 1 | 6 | 7 | 8 | 2 | 4 | 5 | 3 |
| 3 | 4 | 3 | 5 | 4 | 1 | 6 | 7 | 8 | 2 | 8 | 5 | 7 |
| 4 | 4 | 3 | 6 | 4 | 1 | 6 | 7 | 8 | 2 | 9 | 5 | 7 |
| 5 | 2 | 7 | 3 | 6 | 4 | 3 | 7 | 4 | 5 | 4 | 6 | 2 |
| 6 | 4 | 7 | 6 | 6 | 4 | 3 | 1 | 4 | 3 | 4 | 6 | 2 |
| 7 | 2 | 5 | 6 | 6 | 4 | 3 | 1 | 4 | 3 | 4 | 6 | 2 |
| 8 | 8 | 3 | 5 | 2 | 4 | 6 | 6 | 7 | 1 | 9 | 4 | 3 |
| 9 | 8 | 6 | 5 | 2 | 4 | 1 | 6 | 7 | 5 | 9 | 4 | 3 |
| 10 | 8 | 6 | 5 | 2 | 2 | 1 | 6 | 7 | 1 | 9 | 4 | 3 |
| 11 | 8 | 6 | 5 | 2 | 3 | 1 | 6 | 7 | 1 | 9 | 4 | 3 |
| 12 | 4 | 5 | 7 | 7 | 8 | 2 | 4 | 1 | 6 | 4 | 3 | 6 |
| 13 | 8 | 5 | 7 | 7 | 8 | 2 | 4 | 1 | 6 | 4 | 3 | 3 |
| 14 | 7 | 5 | 8 | 2 | 8 | 7 | 6 | 1 | 4 | 2 | 3 | 4 |
| 15 | 3 | 5 | 4 | 2 | 8 | 7 | 6 | 3 | 4 | 5 | 3 | 7 |
| 16 | 2 | 5 | 4 | 2 | 8 | 7 | 6 | 3 | 4 | 6 | 3 | 5 |
| 17 | 2 | 5 | 4 | 2 | 4 | 7 | 6 | 3 | 2 | 6 | 3 | 5 |
| 18 | 2 | 5 | 4 | 2 | 4 | 7 | 6 | 3 | 2 | 4 | 3 | 6 |
| 19 | 2 | 5 | 4 | 2 | 4 | 6 | 5 | 3 | 2 | 4 | 3 | 6 |
| 20 | 5 | 4 | 6 | 2 | 4 | 6 | 5 | 3 | 2 | 4 | 3 | 6 |
|
|
|
Таблица 9 –Данные задания 7 «Транспортная задача»
|
|
|
| № | 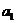
| 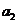
| 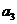
| 
| 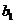
| 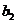
| 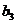
|
| 1 | 30 | 40 | 50 | 10 | 40 | 70 | 20 |
| 2 | 25 | 45 | 50 | 10 | 35 | 65 | 20 |
| 3 | 20 | 40 | 45 | 10 | 35 | 65 | 20 |
| 4 | 20 | 40 | 55 | 10 | 35 | 70 | 20 |
| 5 | 22 | 44 | 54 | 20 | 35 | 70 | 60 |
| 6 | 25 | 45 | 30 | 20 | 35 | 70 | 60 |
| 7 | 25 | 45 | 30 | 20 | 20 | 70 | 60 |
| 8 | 20 | 40 | 30 | 20 | 20 | 70 | 60 |
| 9 | 15 | 40 | 30 | 20 | 20 | 30 | 55 |
| 10 | 15 | 40 | 30 | 15 | 20 | 30 | 55 |
| 11 | 15 | 26 | 30 | 15 | 20 | 32 | 55 |
| 12 | 10 | 25 | 30 | 15 | 40 | 15 | 15 |
| 13 | 10 | 25 | 30 | 35 | 40 | 15 | 15 |
| 14 | 10 | 25 | 30 | 35 | 30 | 30 | 40 |
| 15 | 28 | 25 | 10 | 15 | 34 | 25 | 25 |
| 16 | 20 | 15 | 10 | 15 | 30 | 10 | 20 |
| 17 | 15 | 15 | 10 | 20 | 30 | 10 | 20 |
| 18 | 35 | 15 | 10 | 20 | 30 | 10 | 20 |
| 19 | 23 | 15 | 10 | 20 | 30 | 10 | 25 |
| 20 | 16 | 15 | 10 | 20 | 30 | 10 | 29 |
Пример 7.Решить транспортную задачу, используя следующие данные:

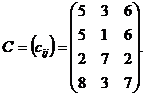
Решение: Транспортная задача называется закрытой если 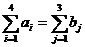 .
.
Проверим модель на сбалансированность:
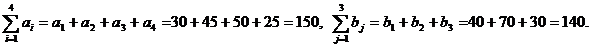
Так как  , условие баланса не выполняется, данная модель является открытой. Приведём задачу к закрытому виду; введём фиктивного потребителя
, условие баланса не выполняется, данная модель является открытой. Приведём задачу к закрытому виду; введём фиктивного потребителя 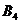 , потребность которого равна
, потребность которого равна 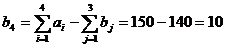 ед. груза. Стоимости перевозки единицы груза (тарифы) для фиктивного потребителя (поставщика) принимаются равными 0.
ед. груза. Стоимости перевозки единицы груза (тарифы) для фиктивного потребителя (поставщика) принимаются равными 0.
|
|
|
Составим исходный план перевозок методом «наименьшего элемента» (минимальной стоимости). Поставки в клетки с нулевыми тарифами осуществляются в последнюю очередь.
1) Выбираем клетку (2,2) с наименьшим «реальным» тарифом равным 1. Записываем в эту клетку максимально возможную поставку 45 ед. груза, т.е. наименьшее из чисел 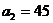 и
и 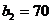 . Исключаем при этом из дальнейшего рассмотрения поставщика
. Исключаем при этом из дальнейшего рассмотрения поставщика 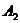 (его возможности полностью исчерпаны). Запомним, что потребитель
(его возможности полностью исчерпаны). Запомним, что потребитель 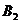 еще нуждается в 70−45=25 ед. груза.
еще нуждается в 70−45=25 ед. груза.
2) Минимальный тариф равный 2 соответствует двум клеткам (3,1) и (3,3) выбираем любую, например клетку (3,1), помещаем в эту клетку 40 ед. груза ( 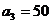 ,
, 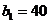 ) и исключаем из рассмотрения потребителя
) и исключаем из рассмотрения потребителя 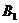 (его потребности полностью удовлетворены). У поставщика
(его потребности полностью удовлетворены). У поставщика 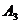 ещё имеется в 50−40=10 ед. груза.
ещё имеется в 50−40=10 ед. груза.
3) Заполним клетку (3,3), которой соответствует минимальный тариф равный 2, поставка в этой клетке равна 10 ( 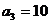 ,
, 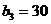 ), исключаем из рассмотрения
), исключаем из рассмотрения 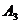 . У потребителя
. У потребителя 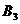 еще имеется потребность в 30−10=20 ед. груза.
еще имеется потребность в 30−10=20 ед. груза.
4) В оставшейся части таблицы наименьший тариф 3 соответствует клеткам (1,2) и (4,2), выберем клетку (4,2) и поместим поставку 25 ед. груза ( 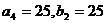 ). Исключаем из рассмотрения два пункта
). Исключаем из рассмотрения два пункта 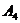 и
и 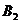 одновременно, поэтому в клетку (4,3), стоящую рядом с клеткой (4,2) запишем 0.
одновременно, поэтому в клетку (4,3), стоящую рядом с клеткой (4,2) запишем 0.
5) В клетку (1,3) помещаем 20 ед. груза (  ), исключаем потребителя
), исключаем потребителя 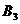 . При этом у поставщика
. При этом у поставщика  еще имеется в 30−20=10 ед. груза.
еще имеется в 30−20=10 ед. груза.
6) Заполним последнюю оставшуюся клетку (1,4) поставкой 10 единиц груза. Все запасы распределены, а потребности удовлетворены.
В опорном плане число занятых поставками клеток должно быть равно числу  .
.
| План-1 | 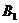 40
40
| 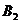 70
70
| 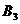 30
30
| 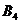 10
10
| 
| |||
30

| 5
-1 + | 3 1 | 6 20 − | 0 10 | 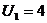
| |||
45
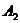
| 5 0 | 1 45 | 6 1 | 0 1 | 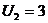
| |||
50
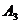
| 2 40 − | 7 9 | 2 + 10 | 0 4 | 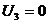
| |||
25
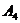
| 8 1 | 3 25 | 7 0 | 0 -1 | 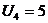
| |||
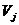
| 
| 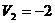
| 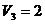
| 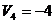
| 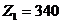
|
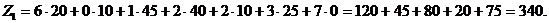
Проверим полученный план на оптимальность методом потенциалов:
а) Потенциалами строк – и столбцов –
и столбцов – 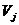 называются числа, удовлетворяющие условию
называются числа, удовлетворяющие условию 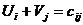 для базисных переменных (для заполненных клеток).
для базисных переменных (для заполненных клеток).
Так как система для определения потенциалов содержит на одно уравнение меньше, чем число потенциалов, то, чтобы найти решение системы потенциалов, один потенциал задаём произвольно, например, 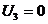 .
.
Остальные потенциалы найдём, решая систему уравнений:
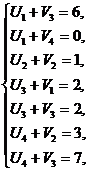
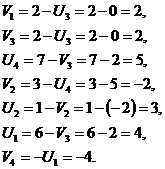
б) Определяем характеристики для свободных клеток по формуле 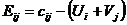 и запишем их в левом нижнем углу свободных клеток. План является оптимальным если все
и запишем их в левом нижнем углу свободных клеток. План является оптимальным если все 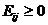 .
.
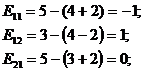
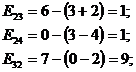


План 1 не оптимален, так как  и
и 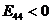 .
.
Улучшим план. Выберем клетку с наименьшей отрицательной характеристикой, например, клетку (1,1) пометим знаком «+» и построим для неё контур:
(1,1)  (1,3)
(1,3)  (3,3)
(3,3) 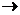 (3,1).
(3,1).
Контур удовлетворяет следующим условиям: это замкнутая ломаная, состоящая из вертикальных и горизонтальных отрезков; отрезки контура могут пересекаться; все вершины контура находятся в заполненных клетках, за исключением той клетки, для которой он строится; число вершин ─ чётное.
Клетки, в которых находятся вершины контура, поочередно помечаем знаками «+» и «─». Из клеток, помеченных знаком «─», выбираем наименьшую поставку  . Число
. Число 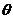 перераспределяется по контуру, в клетках со знаком «+» добавляется
перераспределяется по контуру, в клетках со знаком «+» добавляется  , в клетках со знаком «─» отнимается
, в клетках со знаком «─» отнимается  . После перераспределения груза, только одна вершина контура становится свободной.
. После перераспределения груза, только одна вершина контура становится свободной.
Строим новый план перевозок.
| План-2 |  40
40
|  70
70
| 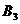 30
30
| 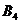 10
10
| 
|
30

|  5 5
 20
+ 20
+
| 3 2 | 6 1 | 0
 10
− 10
−
| 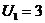
|
45
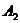
| 5 1 | 1 45 | 6 2 | 0 1 | 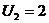
|
50
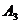
|  ─ 2
20 ─ 2
20
| 7 9 |  + 2
30 + 2
30
| 0 3 | 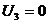
|
25
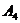
| 8 1 | 3 25 | ─ 7
 0 0
| + 0 -2 | 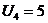
|
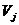
| 
| 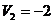
| 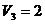
| 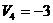
| 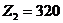
|
Затраты на реализацию плана 2 составляют: 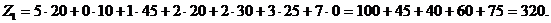
Найдем потенциалы строк и столбцов, для чего составим систему уравнений. Потенциал 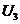 примем равным 0.
примем равным 0.
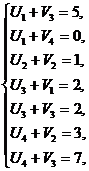
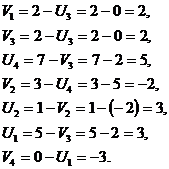
Определим характеристики для свободных клеток.


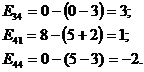
План 2 не является оптимальным, т.к. 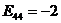
После применения, рассмотренного выше алгоритма, получили план 3.
| План-3 | 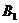 40
40
| 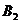 70
70
| 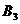 30
30
| 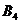 10
10
| 
|
30

| 5 20 | 3 0 | 6 1 | 0 10 | 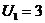
|
45
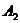
| 5 2 | 1 45 | 6 3 | 0 2 | 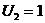
|
50
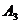
| 2 20 | 7 7 | 2 30 | 0 3 | 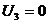
|
25
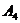
| 8 3 | 3 25 | 7 2 | 0 0 | 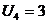
|
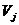
| 
| 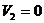
| 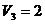
| 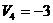
| 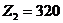
|
План 3 является оптимальным, т, к. все  . Затраты на реализацию оптимального плана составляют
. Затраты на реализацию оптимального плана составляют 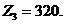
Дата добавления: 2018-04-15; просмотров: 249; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

