Обусловленность квадратурных формул
Квадратурная формула – это равенство вида I* =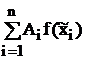 
, где 
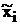– некоторые точки на [a, b] (узлы квадратурной формулы); Ai – коэффициенты квадратурной формулы.
Квадратурная формула – обобщающее название для класса формул численного интегрирования, в которых используются только значения подынтегральной функции (существуют также формулы, использующие производные подынтегральной функции).
Пример квадратурной формулы – составная формула трапеций:
I* = h×
.
В ней A0 = An = h/2, A1 =…= An–1 = h. Составная формула Симпсона также является квадратурной.
Известно (см. пример 1.8 в «Вычислительной практике»), что задача аналитического вычисления определённого интеграла хорошо обусловлена и nD = b – a. Проанализируем теперь задачу численного интегрирования, использующую квадратурную формулу.
Пусть вместо точных значений f(x) подынтегральной функции имеем приближённые значения f*(x) и "xÎ[a, b] £ D(f*) (D(f*) – оценка погрешности). Тогда
D(I**) = | I* – I** | =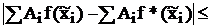 
.
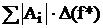Здесь I* – результат вычислений по квадратурной формуле без погрешности, I** – результат вычислений с погрешностью. Следовательно nD =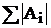 
.
Т.к. все квадратурные формулы абсолютно точны для многочленов 0-й степени, то b – a = 
= 
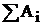×1. Значит 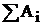= b – a. Отсюда следует, что если в квадратурной формуле все Ai > 0, то nD = b – a как и для аналитической задачи, а если среди Ai есть отрицательные, то nD > b – a.
Задание. Проверить непосредственно, что для составной формулы трапеций 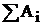= b – a.
|
|
|
Тема 5. Численное решение обыкновенных дифференциальных
Уравнений (ОДУ)
Решение ОДУ – одна из наиболее популярных вычислительных задач, она возникает во многих приложениях.
Основные понятия
ОДУ – это уравнение вида
F(x, y,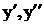 
,…) = 0 (5.1)
Порядок дифференциального уравнения – это порядок старшей используемой производной. Решение дифференциального уравнения – это функция у = у(х), которая при подстановке в уравнение (1) превращает его в тождество.
Уравнение (1) не имеет однозначного решения, чтобы получить его, надо помимо самого уравнения задать дополнительные условия. По типу дополнительных условий различают одноточечные и многоточечные задачи. В одноточечных задачах все условия задаются в одной точке (при одном и том же х). Обычно это начальная точка х0. В этом случае говорят, что поставлена задача Коши.
Пример 5.1. Задача Коши:
.
В многоточечной задаче дополнительные условия задаются в нескольких точках. Часто это границы отрезка определения решения. Тогда говорят, что поставлена краевая задача.
Пример 5.2. Краевая задача:
.
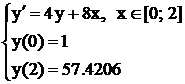Несложно убедиться, что задачи примеров 5.1 и 5.2 имеют одинаковое решение у = 1.125 е2х – 0.125 е–2х – 2х.
|
|
|
Наиболее важной является задача Коши для уравнения 1-го порядка – к ней сводятся многие другие задачи.
Аналитическое решение ОДУ – это аналитически заданная функция у(х) (см. примеры 5.1 и 5.2). Численное решение – таблица значений функции у(х) в дискретных точках (в узлах). Так численное решение задач примеров 5.1 и 5.2 является таблица 5.1.
| Таблица 5.1. | ||||
| Численное решение примеров 5.1 и 5.2 | ||||
| х | 0 | 0.2 | … | 2.0 |
| у | 1 | 1.1945 | … | 57.4206 |
Дата добавления: 2018-04-15; просмотров: 318; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!