Частные производные функции нескольких переменных.

       Определение. Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина Dxz = f( x + Dx, y) – f(x, y) называется частным приращением функции по х.

Можно записать 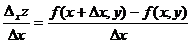. Тогда  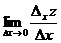называется частной производной функции z = f(x, y) по х.

       Обозначение: 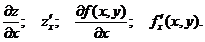 Аналогично определяется частная производная функции по у.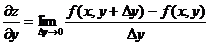

       Геометрическим смыслом частной производной (допустим 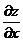) является тангенс угла наклона касательной, проведенной в точке N0(x0, y0, z0) к сечению поверхности плоскостью у = у0.

Частные производные высших порядков.

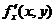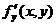Если функция f(x, y) определена в некоторой области D, то ее частные производные  и  тоже будут определены в той же области или ее части.

     Будем называть эти производные частными производными первого порядка.

Производные этих функций будут частными производными второго порядка.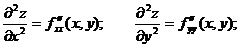

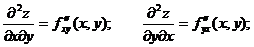
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

       Определение. Частные производные вида 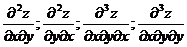и т.д. называются смешанными производными.

 

Тема 5:ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ

 

Лекция № 9. Числовые и функциональные ряды

План:

1. Основные понятия.

2. Признаки сходимости рядов.

3. Знакочередующиеся ряды. Знакопеременные ряды.

 

Основные понятия.

       Определение: Числовым рядом называется бесконечная последовательность чисел u₁, u₂…u_n…, соединенных знаком сложения: u₁ +u₂+…+u_n+…=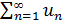

       Числа u₁, u₂…u_n – называются членами ряда, член u_n – называется общим или n-ым членом ряда.

Ряд считается заданным, если известен его общий член: u_n=f(n), n=1,2,…

Пример:

1) 2+5+8+11+14+… общий член равен u_n=2+3(n-1)

2) +…общий член u_n=

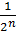
       Определение: Частичной суммой ряда называется сумма первых n –слагаемых ряда. Обозначается:S_n

       Определение: Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т. е. 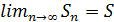, S- сумма ряда.

       Определение: Если конечный предел последовательности частичных сумм не существует или равен ∞, то ряд называется расходящимся.

       Пример: Найти сумму ряда: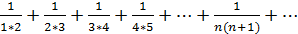

Решение: Составим частичную сумму: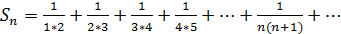

Учитывая, что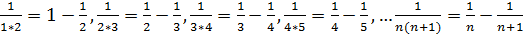                                                                                            

Тогда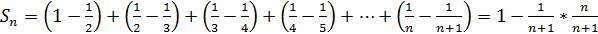

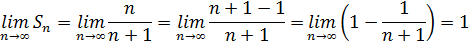
Следовательно, S=1

Свойства сходящихся рядов:

1. Если ряд u₁ +u₂+…+u_n+… сходится и имеет сумму S, то и ряд

λu₁ +λu₂+…+λu_n+…,полученный умножением данного ряда на число λ, также сходится и имеет сумму λS

2. Если ряды u₁ +u₂+…+u_n+… и v₁ +v₂+…+v_n+… сходятся и их суммы соответственно равны S₁ и S₂, то ряд (u₁ + v₁)+(u₂+ v₂)+…+(u_n+v_n)+…, представляющий собой сумму данных рядов, также сходится и его сумма равна S=S₁+S₂

3. Если ряд сходится, то сходится и ряд, полученный из данного ряда путем отбрасывания или приписывания конечного числа членов.

Определение: Ряд, полученный из данного ряда отбрасыванием его первых n-членов, называется n-ым остатком ряда и обозначается r_n

4. Для того чтобы ряд сходился необходимо и достаточно, чтобы при n→∞ остаток ряда стремился к нулю, т.е.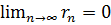

 

Признаки сходимости рядов.

       Теорема: (Необходимый признак сходимости).Если ряд сходится, то предел его общего члена u_n при n→∞ равен нулю, т. е.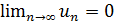

       Следствие: Если предел общего члена ряда u_n при n→∞ не равен нулю, т. е. , то ряд расходится

       Пример: Исследовать сходимость ряда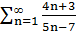

Решение: , следовательно, необходимый признак сходимости не выполняется, следовательно, ряд расходится.
       Замечание: Рассмотренная теорема выражает лишь необходимый признак, но недостаточный признак сходимости ряда. Если 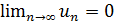, то из этого еще не следует, что ряд сходится. (Например: 1+  )

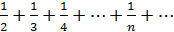       Теорема: (Признак сравнения). Пусть даны два ряда с положительными членам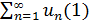и  и , при чем члены первого не превосходят членов второго ряда, т.е при любом n ≤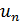

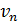
     Тогда:

1. Если сходится второй ряд, то сходится и первый ряд

2. Если расходится первый ряд, то расходится и второй ряд.

     Пример: Исследовать сходимость ряда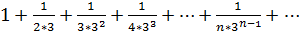

       Решение: Сравним данный ряд со сходящимся геометрическим рядом: +…+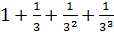

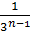
Члены данного ряда, начиная со второго, меньше членов сходящегося геометрического ряда 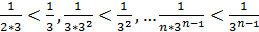, то на основании признака сравнения исходный ряд сходится

                «Эталонные ряды», используемые для сравнения:

1. Геометрический ряд 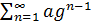 сходится при  и расходится при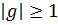

2. Гармонический ряд 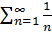 расходится

3. Обобщенный гармонический ряд 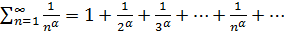 сходится при α>1 и расходится при α≤1

       Теорема: (Предельный признак сравнения). Есл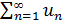и и 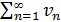 ряды с положительными членами и существует конечный предел отношения их общих членов 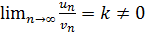, то ряды одновременно сходятся, либо расходятся

     Пример: Исследовать сходимость ряда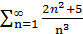

Решение: Сравним данный ряд с расходящимся гармоническим рядом  (выбор такого ряда для сравнения может подсказать то, что при больших n 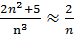). Так как 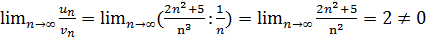, то ряд расходится, т. к. расходится гармонический ряд.

       Теорема (Признак Даламбера). Пусть для ряда 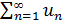 с положительными членами существует предел отношения (n+1) – го члена к n – му члену 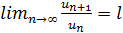. Тогда, если l<1, то ряд сходится, если l>1, то ряд расходится, если l=1, то вопрос о сходимости ряда остается нерешенным.

                     Пример 1: Исследовать сходимость ряда: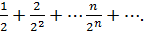

       Решение:Составим предел отношения

.

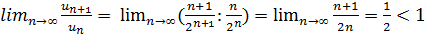По признаку Даламбера ряд сходится.

                     Пример 2: Исследовать сходимость ряда: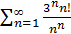

       Решение:Составим предел отношения

                     Указание: (n+1)!=n!(n+1)

         По признаку Даламбера ряд расходится.

                     Замечание: Если 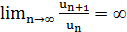, то ряд расходится.

       Теорема (Признак Коши).Если для ряда с положительными членами u₁+u₂+u₃+…+u_n+… величина 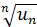 имеет конечны предел l при n→∞, т. е. 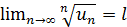, то:

1. если l<1, то ряд сходится

2. еслиl>1, то ряд расходится

  Пример: Исследовать сходимость ряда

  Решение: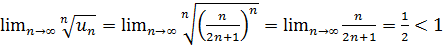

Следовательно, ряд сходиться

       Теорема (интегральный признак сходимости). Пусть дан ряда 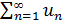, члены которого положительны и не возрастают, т.е. u₁≥u₂≥u₃≥…≥u_n≥…, а функция f(x), определенная при x≥1, непрерывная и невозрастающая и f(1)=u₁, f(2)=u₂,…f(n)=u_n,…Тогда для сходимости ряда  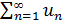необходимо и достаточно, чтобы сходился несобственный интеграл

                Пример: Исследовать сходимость обобщенного гармонического ряда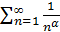    

       Решение: Пусть f(x)= 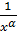. Функция f(x) при x>0 (а значит и при x≥1) положительная и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла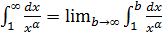

Если α=1,то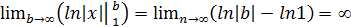

Если α≠1, то

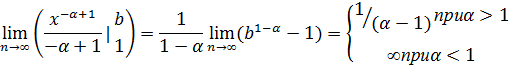
Данный ряд сходится при  и расходится при .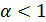

 

---

Дата добавления: 2018-05-01; просмотров: 282; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

⇐ Предыдущая123456Следующая ⇒

---

Мы поможем в написании ваших работ!