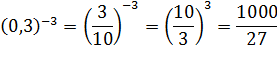Алгоритм решения неравенств второй степени
Для понимания и применения правил (свойств, формул) необходимо ЗНАТЬ определения терминов: слагаемое, сумма, множитель, произведение, делимое, делитель, частное, обыкновенная дробь (числитель дроби и знаменатель дроби), положительные (отрицательные) числа, абсцисса точки, ордината точки, высота, биссектриса, медиана, средняя линия треугольника, равнобедренный треугольник (боковые стороны, основание, вершина), равносторонний треугольник, прямоугольный треугольник (катет и гипотенуза), диагональ четырехугольника, параллелограмм, ромб, квадрат, трапеция (боковые стороны, основание), равнобедренная трапеция, серединный перпендикуляр, периметр фигуры. Если вы не понимаете какое-то слово из правила (свойства, формулы) – его нужно обязательно ПОНЯТЬ!!!(взять из учебников, справочников, интернета)! Иначе смысл выученного – пропадает.
АРИФМЕТИКА
Правило сложения и вычитания десятичных дробей:
При сложении (вычитании) десятичные дроби записывают столбиком так, чтобы запятые находились друг под другом. Затем складывают (вычитают) как обыкновенные числа. В ответе –запятую ставят под запятыми.
Правило умножения десятичных дробей:
При умножении десятичные дроби перемножают столбиком как обыкновенные числа. В полученном произведении отделяют справа запятой столько цифр, сколько их у перемножаемых дробей вместе взятых.
|
|
|
Правило деления десятичных дробей:
При делении преобразуют дробь, на которую делят, в целое число. Для этого в этой дроби сдвигают запятую вправо на нужное количество цифр. Затем в первой дроби сдвигают запятую на то же количество цифр и делят полученное число на целое число.
Основное свойство обыкновенной дроби:
Если числитель и знаменатель дроби умножить (или разделить) на одно и то же число, получим дробь равную первоначальной дроби.
Правило сложения и вычитания обыкновенных дробей с одинаковыми знаменателями:
При сложении (вычитании) дробей с одинаковыми знаменателями – числители складываются (вычитаются), а знаменатель остается тем же.(Если дроби содержат целую часть, то можно отдельно складывать (вычитать) целые и дробные части).
Правило сложения и вычитания обыкновенных дробей с разными знаменателями:
При сложении (вычитании) дробей с разными знаменателями – дроби надо стачала привести к одинаковому знаменателю (используя основное свойство обыкновенной дроби), и только потом складывать (вычитать).
Правило умножения обыкновенных дробей:
Чтобы умножить дробь на дробь, надо перемножить их числители (это будет числитель новой дроби) и знаменатели (это будет знаменатель новой дроби). (Если дроби содержат целую часть – то вначале их надо преобразовать в неправильные дроби!)
|
|
|
Правило деления обыкновенных дробей:
Чтобы разделить дробь на дробь, надо первую дробь умножить на дробь обратную («переверную») второй. (Если дроби содержат целую часть – то вначале их надо преобразовать в неправильные дроби!)
Правило сравнения обыкновенных дробей:
Из двух дробей с одинаковыми знаменателями, больше та – числитель которой больше. Если дроби с разными знаменателями – то их надо привести к общему знаменателю, а затем сравнивать.
Правила сложения чисел с разными знаками:
1) Если в примере два минуса, то в сумме ставим минус, а сами числа складываем (пример: - 2 – 10 = - (2 + 10) = - 12).
2) Если складываем числа с разными знаками, то в сумме ставим тот знак, который стоит перед бОльшим числом, и из бОльшего числа вычитаем меньшее. (пример1: -8 + 3 = -5 так как, 8 больше 3, значит в сумме будет знак минус, 8-3=5; пример2: 20 – 28 = +20 – 28 = - 8 так как 28 больше 20, значит в сумме будет знак минус, 28-20=8; пример3: -5 + 12 = 7 так как 12 больше 5, то в сумме ставим знак плюс, 12-5=7).
|
|
|
Правило умножения (деления) чисел с разными знаками:
Если умножить (разделить) числа с одинаковыми знаками, то в результате получим положительное число. Если умножить (разделить) числа с разными знаками, то в результате получим отрицательное число.
Основные формулы сокращенного умножения:
(а ± в)2 = а2 ± 2ав + в2;
(а – в) · (а + в) = а2 – в2
ГЕОМЕТРИЯ:
Основные свойства треугольника:
1) Сумма углов любого треугольника равна 180°.
2) Внешний угол треугольника равен сумме двух других углов не смежных с ним.
3) Высоты, медианы, биссектрисы и серединные перпендикуляры треугольника пересекаются в одной точке (каждые линии в своей точке!)
4) Медианы треугольника точкой пересечения делятся в отношении 2 к 1 считая от вершины.
5) Центром вписанной в треугольник окружности является точка пересечения биссектрис.
6) Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к его сторонам.
7) Средняя линия треугольника параллельна одной из его сторон и равна ее половине.
|
|
|
8) Площадь треугольника равна половине произведения высоты на основание.
Основные свойства равнобедренного треугольника:
1) Равнобедренный треугольник обладает всеми свойствами обыкновенного треугольника.
2) Углы при основании равнобедренного треугольника равны.
3) Высота, проведенная из вершины равнобедренного треугольника, является так же его биссектрисой и медианой.
4) Высоты, биссектрисы и медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.
Основные свойства равностороннего (правильного) треугольника:
1) Равносторонний треугольник обладает всеми свойствами обыкновенного и равнобедренного треугольника.
2) Углы равностороннего треугольника равны между собой и равны по 60°.
3) Высота, проведенная из любой вершины равностороннего треугольника, является его биссектрисой и медианой.
4) Высоты, медианы, биссектрисы и серединные перпендикуляры к сторонам равностороннего треугольника пересекаются в ОДНОЙ (общей!) точке.
5) Центры вписанной и описанной около равностороннего треугольника окружностей – совпадают.
Основные свойства прямоугольного треугольника:
1) Прямоугольный треугольник обладает всеми свойствами обыкновенного треугольника.
2) Сумма острых углов прямоугольного треугольника равна 90°.
3) Катет, лежащей против угла 30°, равен половине гипотенузы.
4) Медиана, проведенная к гипотенузе, равна ее половине.
5) Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы, а сама гипотенуза является диаметром этой окружности.
6) Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов.
7) Чтобы вычислить синус острого угла прямоугольного треугольника, надо противолежащий катет разделить на гипотенузу.
8) Чтобы вычислить косинус острого угла прямоугольного треугольника, надо прилежащий катет разделить на гипотенузу.
9) Чтобы вычислить тангенс острого угла прямоугольного треугольника, надо противолежащий катет разделить на прилежащий катет.
10) Площадь прямоугольного треугольника равна половине произведения его катетов.
Основные свойства параллелограмма:
1) Противоположные стороны параллелограмма параллельны и равны.
2) Противоположные углы параллелограмма равны.
3) Сумма всех углов параллелограмма равна 360°.
4) Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
5) Диагонали параллелограмма точкой пересечения делятся пополам.
6) Площадь параллелограмма равна произведению высоты на основание.
Основные свойства ромба:
1) Ромб обладает всеми свойствами параллелограмма.
2) У ромба все стороны равны.
3) Диагонали ромба перпендикулярны между собой.
4) Диагонали ромба делят его углы пополам (являются биссектрисами углов).
5) Площадь ромба равна половине произведения его диагоналей.
Основные свойства прямоугольника:
1) Прямоугольник обладает всеми свойствами параллелограмма.
2) Все углы прямоугольника равны по 90°.
3) Диагонали прямоугольника равны.
4) Площадь прямоугольника равна произведению его смежных сторон (высоты на длину).
Основные свойства квадрата:
1) Квадрат обладает всеми свойствами параллелограмма и ромба.
2) Все стороны квадрата равны и все углы равны по 90°.
3) Площадь квадрата равна квадрату его стороны.
Основные свойства трапеции:
1) Сумма углов трапеции равна 360°.
2) Сумма углов, прилежащих к боковой стороне трапеции, равна 180°.
3) Площадь трапеции равна полу-сумме оснований, умноженной на высоту.
Основные свойства равнобедренной трапеции:
1) Равнобедренная трапеция обладает всеми свойствами обыкновенной трапеции.
2) Углы при основаниях равнобедренной трапеции равны.
3) Диагонали равнобедренной трапеции равны.
Лекция №1: Линейная функция
•Функцию вида y = kx + bназывают линейной функцией.
Буквенные множители «k» и «b» называютчисловыми коэффициентами (вместо «k» и «b» могут стоять любые числа: положительные, отрицательные или дроби).
Примеры линейных функций:
1) y = 5x + 3, где k = 5, b = 3
2) y = −x + 1, где k = −1, b = 1
3)  , , где k =
, , где k =  , b = - 2
, b = - 2
4) y = 0,5x,где k = 0,5, b = 0.
•Графиком линейной функции y = kx + b является прямая.
Чтобы построить график достаточно найти всего две точки, принадлежащие данной функции (значение для х берем произвольно, у высчитываем при данном значении х), построить эти точки по полученным координатам (х; у) в системе координат и через них провести прямую.
· • Если k>0  , то график функции возрастает (наклонен вправо; движемся «в гору»)
, то график функции возрастает (наклонен вправо; движемся «в гору»)
· Если k<0  , то график функции убывает (наклонен влево; движемся «с горы»).
, то график функции убывает (наклонен влево; движемся «с горы»).
В приведенных выше примерах: 1) функция – возрастает; 2) – убывает; 3) – возрастает
и 4) – также возрастает.
•Коэффициентbпоказывает ординату точки пересечения графика функции с осью ОY (т.е. график проходит через точку с координатами (0; b)).
В приведенных выше примерах: 1) функция пересекает ось ОYв точке (0; 3); 2) в точке (0; 1); 3) в точке (0; -2); 4) в точке (0; 0) – т.е. график (прямая) проходит через начало координат.
•Чтобы проверить принадлежность точки графику функции достаточно подставить координаты точки в формулу функции и выполнить арифметические расчеты:
- Если получится верноеравенство, значит, точка принадлежитграфику функции.
- Если получится неверноеравенство, значит, точкане принадлежитграфику функции.
•Если у линейных функций коэффициенты k равны, то графиками этих функций являются параллельные прямые.
Например графиками функций 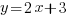 ;
; 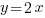 ;
;  являются параллельные прямые.
являются параллельные прямые.
Лекция № 2:Обратная пропорциональность
| •Обратной пропорциональностью называется функция вида: | 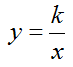
|
где k ≠ 0 и является числом.
Примеры:
1) 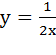 ; где k =
; где k = 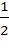 ; 2)
; 2) 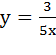 ; где k =
; где k = 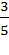 ; 3)
; 3) 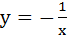 ; где k= -1.
; где k= -1.
•Областью определения функции 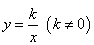 является множество всех действительных чисел, кроме x=0, т.е.
является множество всех действительных чисел, кроме x=0, т.е. 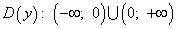
•Областью значений функции являются все числа, кроме y=0, т.е. 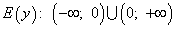
•Графиком обратной пропорциональности является гипербола.
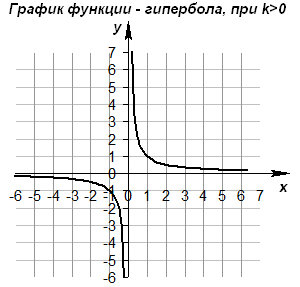
•Если k>0  , то ветви гиперболы расположены в IиIIIкоординатных четвертях , то ветви гиперболы расположены в IиIIIкоординатных четвертях
| 
|
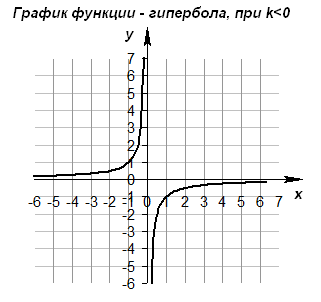
•Если k<0  ,то ветви гиперболы расположены во IIиIVкоординатных четвертях ,то ветви гиперболы расположены во IIиIVкоординатных четвертях
| 
|
Лекция № 3:Квадратичная функция.
•Функция видаy = ax2 + bx + c, гдеa, b, c – числа, причем а ≠ 0  называется
называется
Квадратичной функцией.
•Графиком квадратичной функции является парабола.
•Если коэффициент a>0, то ветви параболы напрaвлены вверх,
Если коэффициент a<0, то ветви параболы напрaвлены вниз.
•Координаты вершины параболыО' (х0; у0), где х0= 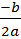 ; у0= у(х0).
; у0= у(х0).
•Точка пересечения параболы с осью OY имеет координаты (0;c).
•(х1;0) и (х2; 0)- координаты точек пересечения параболы с осью ОХ,
где х1и х2– корни уравнения ax2 + bx + c = 0.
Алгоритм построения графика квадратичной функции:
1. Привести запись формулы функции к виду: y = ax2 + bx + c.
2. Выписать значения коэффициентов a, b, иc.
3. По знаку коэффициента а, определить направление ветвей параболы.
4.Найти координаты вершины параболы О'.
5.Найти координаты точкипересечения параболы с осью OY.
6. Найти координаты точкипересечения параболы с осьюОХ.
7. Построить параболу, проходящую через найденные точки.
Лекция № 4: Свойства степени с целым показателем.
| Правило/свойство | Формула | Примеры |
| Чтобы возвести число(выражение) в n-ную степень, над это число(выражение) умножить само на себя nраз |
аn = 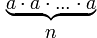
| 53 = 5 * 5 * 5 = 125;
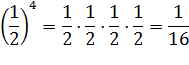
|
| Любое число(выражение) в 1-ой степени равно самому числу(выражению) | а1= а | 81 = 8; (-17)1 = -17; (2х)1 = 2х |
| Любое число(выражение) в 0-ой степени равно 1 | а0= 1 | 120 = 1; (-329)0 = 1; (15xy)0 = 1 |
| Ноль в любой степени равен нулю | 0n = 0, где п>0 | 015 = 0 |
| Единица в любой степени равна единице | 1n = 1 | 165 = 1; 1-48 = 1 |
| При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным | an• ak=an+k | 52• 510 = 52+10 = 512; х7• х-3 = 57+(-3)= х4; сk• c8 = ck+8 |
| При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным | 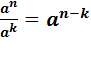 или
an: ak или
an: ak 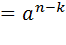
| 28 : 23 = 28-3 = 25;
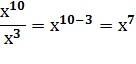
|
| При возведении степени в степень показатели перемножаются | (аn)k = ank | (23)8 = 23*8 = 224; (с6)-5 = с-30; (53)k = 53k |
| При возведении в степень произведения в эту степень возводится каждый множитель | (a · b)n = an · b n | (3x2)3 = 33•(x2)3 = 27x6 |
| При возведении в степень дроби в эту степень возводятся числитель и знаменатель | (a / b)n = an / bn | 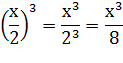
|
| Чтобы возвести число(выражение)в отрицательную степень (-n) надо 1 разделить на это число(выражение) в степени n | 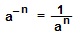
| 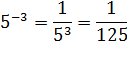
|
| Чтобы возвести в отрицательную степень (-n) обыкновенную дробь, надо дробь «перевернуть» и возводить ее в степень n | 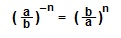
| 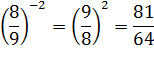
|
| Чтобы возвести в отрицательную степень (-n) десятичную дробь, надо ее вначале записать в виде обыкновенной дроби |
| |
| Чтобы возвести 10 в n-ную степень, надо за 1 дописать n нулей | 107 = 10000000(семь нулей) | |
| Чтобы возвести 10 в степень (-n), надо перед 1 написать n нулей (первый 0 отделить запятой) |
10-7 = 0,0000001 (всего перед 1 семь нулей!) | |
| Чтобы умножить десятичную дробь на 10n, надо перенести запятую на n цифр вправо | 15,26894 •103 = 15268,94 | |
| Чтобы умножить десятичную дробь на 10-n, надо перенести запятую на n цифр влево | 15,26894 •10-3 = 0,01526894 | |
Алгоритм решения линейных уравнений:
1. Преобразовать выражения, входящие в уравнение: раскрыть скобки, привести подобные слагаемые (если в уравнении есть дроби – то умножить обе части уравнения на общий знаменатель дробей).
2. Перенести слагаемые с переменной в левую часть, а числа – в правую (при переносе – необходимо поменять знаки переносимых слагаемых на противоположные).
3. Привести подобные слагаемые (если в этом есть необходимость), пока в левой части уравнения не останется одно слагаемое с переменной, а в правой - одно число.
4. Разделить обе части уравнения на число, стоящее перед переменной.
5. Записать ответ.
Пример 1: Решить уравнение 3(х - 2) – 1 = 4х + 2
Раскроем скобки: 3х – 6 – 1 = 4х + 2
Приведем в левой части подобные слагаемые: 3х – 7 = 4х + 2
Перенесем слагаемые с х в левую часть, а числа – в правую: 3х - 4х = 2 + 7
Снова приведем подобные слагаемые: -х = 9
Разделим обе части уравнения на (-1): х = -9
Ответ: х = -9
Пример 2:Решить уравнение 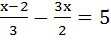
Чтобы решить линейное уравнение с дробями, удобно избавиться от знаменателей.
Для этого нужно найти наименьший общий знаменатель всех входящих в уравнение дробей и обе части уравнения умножить на это число. Наименьший общий знаменатель данных дробей равен 6.
Дополнительный множитель к первой дроби равен 2, ко второй — 3, к 5 — 6. Умножаем обе части уравнения на наименьший общий знаменатель:
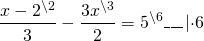
В результате наименьший общий знаменатель и знаменатель каждой дроби сокращаются, и получаем линейное уравнение, не содержащее дробей: 
Раскроем скобки и приведём подобные слагаемые:
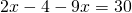
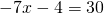
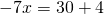
Обе части уравнения делим на число, стоящее перед иксом:
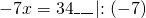
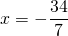
Из полученной неправильной дроби выделяем целую часть
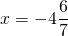
Ответ: 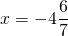
Алгоритм решения квадратных уравнений:
Пусть дано квадратное уравнение ax2 + bx + c = 0.
Тогда дискриминант — это число D,которое можно найти по формулеD= b2 − 4ac.
• Если дискриминант D > 0, корни можно найти по формулам:
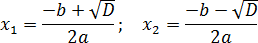
• Если D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом.
• Если D < 0, корней нет — ничего считать не надо.
Примечание: Если уравнение содержит скобки или слагаемые в нем переставлены местами, то надо сначала его привести к стандартному виду: ax2 + bx + c = 0, а затем решать как сказано выше.
Пример: Решить уравнение: x2 − 2x − 3 = 0
Уравнение записано в стандартном виде, значитa = 1; b = −2; c = −3.
Вычислим дискриминант: D = (−2)2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
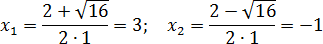
Ответ: х1=3; х2= -1.
Лекция № 5:Задачи на %.
• 1% - это одна сотая часть числа.
Проценты можно записывать в виде обыкновенных или десятичных дробей:
| % | Запись в виде обыкновенной дроби | Запись в виде десятичной дроби |
| 1% | 1/100 | 0,01 |
| 5% | 5/100 | 0,05 |
| 10% | 10/100 или 1/10 | 0,1 |
| 12% | 12/100 | 0,12 |
| 30% | 30/100 или 3/10 | 0,3 |
| 48% | 48/100 | 0,48 |
| 96% | 96/100 | 0,96 |
| 100% | 100/100 или 1 | 1 |
| 108% | 108/100 | 1,08 |
| 164% | 164/100 | 1,64 |
| 200% | 200/100 или 2 | 2 |
| 333% | 333/100 | 3,33 |
•Чтобы найти % от числа – надо это число умножить на % (записанный в виде обыкновен-ной или десятичной дроби).
Пример: Найти 48% от 200.
Решение: 200 * 48/100 = 96 или 200 * 0,48 = 96.
Задачи на цену товара
•При решении задач на стоимость товара необходимо первоначальную цену принимать за
100%.
Пример 1: Товар стоил 800 руб. Цена товара снизилась на 15%. Найти новую цену товара.
Решение:
1 способ: Первоначальная цена – 100%. Новая цена 100% - 15% = 85% от прежней цены. Т.е. надо найти 85% от 800: 800 * 85/100 = 680 руб.
2 способ – составление пропорции: Первоначальная цена – 100%,
новая цена 100% - 15% = 85%.
Составим пропорцию: % записываем под %, рубли – под рублями:
800 руб. – 100%
х руб. – 85%; тогда х = 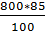 = 680 руб. – новая цена товара.
= 680 руб. – новая цена товара.
Пример 2: Товар стоил 800 руб. Цена товара увеличилась на 30%. Найти новую цену товара.
Решение:
1 способ: Первоначальная цена – 100%. Новая цена 100% + 30% = 130% от прежней цены. Т.е. надо найти 130% от 800: 800 * 130/100 = 1040 руб.
2 способ – составление пропорции: Первоначальная цена – 100%.
новая цена 100% + 30% = 130%.
Составим пропорцию:
800 руб. – 100%
х руб. – 130%; тогда х = 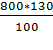 = 1040 руб. – новая цена товара.
= 1040 руб. – новая цена товара.
Пример 3: Товар стоил 2800 руб. После скидки товар стал стоить 2520 руб. На сколько процентов снизилась цена товара?
Решение: Составим пропорцию (первоначальную цену – берем за 100%):
2800 руб. – 100%
2520 руб. – х%; тогда х =  = 90%.
= 90%.
Таким образом, товар стоил 100%, новая цена составила 90% от первоначальной, значит
100% - 90% = 10%.
Ответ: цена товара снизилась на 10%.
Пример4: После скидки на 15% товар стал стоить 2000 руб. Найти первоначальную цену товара.
Решение: Составим пропорцию (первоначальную цену – берем за 100%,
новая цена 100% - 15% = 85% от первоначальной цены):
х руб. – 100%
2000 руб. – 85%; тогда х = 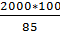 = 2352,94 руб. – стоил товара первоначально.
= 2352,94 руб. – стоил товара первоначально.
Задачи на доли
Пример5: Для приготовления фарша взяли говядину и свинину в отношении 2 : 24.
Сколько % в полученном фарше составляет говядина?
Решение: 2 и 24 – это части ЦЕЛОГО, значит ЦЕЛОЕ состоит из 2 + 24 = 26 частей!
Составим пропорцию (ЦЕЛОЕ – берем за 100%):
26 частей – 100%
2 части(говядина) – х%; тогда х = 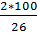 = 7,7%. – составляет в фаршеговядина.
= 7,7%. – составляет в фаршеговядина.
Алгоритм решения неравенств второй степени
С одной переменной
(метод интервалов/промежутков)
1. Привести запись неравенства к виду ax2 + bx + c> 0(< 0; ≤ 0; ≥ 0).Т.е. чтобы справа остался ноль!
2. Найти те значения переменной х, которые обращают левую часть неравенства в ноль (т.е. из уравнения ax2 + bx + c = 0найти корних1 и х2 ).
3. Отметить значения х1 и х2 на числовой оси (пустыми или закрашенными точками, в зависимости от знака решаемого неравенства: «строгое» или нет), разбив тем самым числовую ось на интервалы/промежутки.
4. Посчитать знак уравнения ax2 + bx + c = 0 в одном из промежутков.
5. Проставить знаки в остальных промежутках, учитывая принцип чередования знаков.
6. Записать в ответ те промежутки, знаки которых удовлетворяют решаемому неравенству.
Примечание:Если вуравненииax2 + bx + c = 0D = 0 илиD < 0, то решением неравенства будет либо вся числовая ось, либо пустое множество.
Чтобы определить, чтоименно, надо взять ЛЮБОЕ значениеxи подставить в решаемое неравенство.
•Если получим верное неравенство, то решением является ЛЮБОЕ x(вся числовая ось);
•Если получим неверное неравенство, то решением является пустое множество.
Лекция № 6: Окружность: углы, касательная.
| • Угол, с вершиной в центре окружности – называется центральным углом. •Градусная мера центрального угла равна градусной мере дуги на которую он опирается:∡AOB=∪AB | 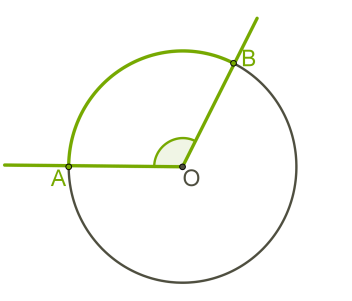
|
| • Угол, вершина которого лежит на окружности, а стороны пересекают ее, - называется вписанным в окружность. •Вписанный угол равен половине дуги, на которую он опирается:∡ACB=1/2 ∪AB | 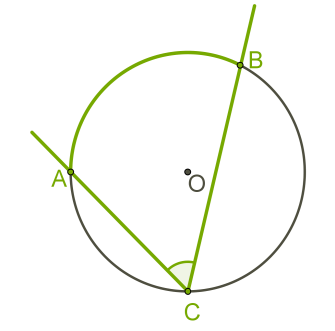
|
| •Если вписанный и центральный углы опираются на одну и ту же дугу, то центральный угол в два раза больше соответствующего вписанного угла: ∡ АОВ = 2 ∡АСВ | |
| •Вписанный угол, опирающийся на диаметр равен 90°. | 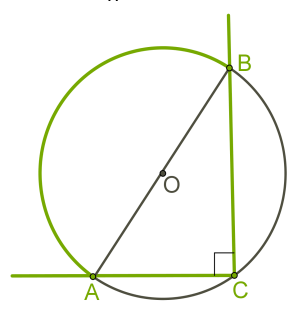
|
| •Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков второй хорды: AM•MB = CM•MD | 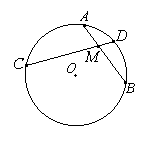
|
| •Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде. | 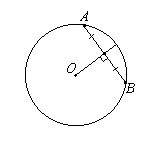
|
| •Радиус, проведенный в точку касания, перпендикулярен касательной. | 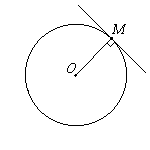
|
| •Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности: АМ= АN и ∡MАО = ∡ОАN | 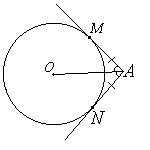
|
| Теорема о касательной и секущей: • Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC2 = MA•MB | 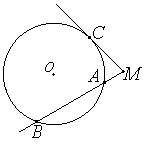
|
| Следствие из теоремы о касательной и секущей: • Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть: MA•MB = MC•MD | 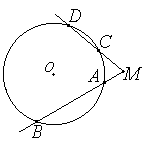
|
Вероятность
| Вероятность события | = | Число благоприятных исходов |
| Общее число исходов |
Средняя линия трапециипараллельна основаниям и равна их полу-сумме:
| Средняя линия трапеции | = | а + b |
| 2 |
, где а и b- основания трапеции
Алгоритм решения линейныхнеравенств:
1. Преобразовать выражения, входящие в неравенство: раскрыть скобки, привести подобные слагаемые (если в неравенстве есть дроби – то умножить обе части неравенства на общий знаменатель дробей).
2. Перенести слагаемые с переменной в левую часть, а числа – в правую (при переносе – необходимо поменять знаки переносимых слагаемых на противоположные).
3. Привести подобные слагаемые (если в этом есть необходимость), пока в левой части неравенства не останется одно слагаемое с переменной, а в правой - одно число.
4. Разделить обе части неравенства на число, стоящее перед переменной (если делим на отрицательное число – то необходимо поменять знак неравенства на противоположный!).
5. Записать ответ в виде числового промежутка.
Пример: Решить неравенство 5(х-2)-2(х+1)<-6
Раскроем скобки: 5х – 10-2х – 2<-6
Приведем в левой части подобные слагаемые: 3х – 12<-6
Оставим слагаемое с х в левой части, а числа перенесем в правую: 3х<-6+12
Снова приведем подобные слагаемые: 3х < 6
Разделим обе части неравенства на 3: х < 2
Ответ: (-∞; 2).
Дата добавления: 2018-04-15; просмотров: 776; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!