ПОСЛІДОВНОСТІ В МЕТРИЧНИХ ПРОСТОРАХ. ЗБІЖНІСТЬ
Нехай маємо метричний простір (X,ρ).
Означення. Якщо кожному  взятому в порядку зростання, поставлено у відповідність елемент
взятому в порядку зростання, поставлено у відповідність елемент  , то кажуть, що задано послідовність {xn} в цьому просторі.
, то кажуть, що задано послідовність {xn} в цьому просторі.
Приклади.
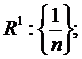
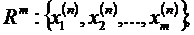
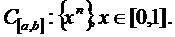
Тут m – розмірність простору, n – загальний член послідовності.
Означення. Елемент а, який належить простору (X,ρ) називають границею послідовності {xn}, якщо для 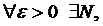 що як тільки
що як тільки 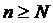 , то
, то 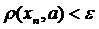 .
.
Теорема 1. Якщо послідовність має границю, то вона єдина.
Доведення. Припустимо, що існує дві границі a та b тоді
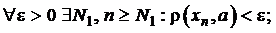
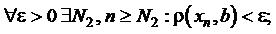
Нехай N=max{N1,N2}, якщо n >N, то обидві нерівності виконуються одночасно. Тоді маємо:  ε, а це означає , що
ε, а це означає , що 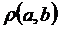 =0, в силу довільності ε. Отже а=b.
=0, в силу довільності ε. Отже а=b.
Теорему доведено.
Теорема 2. Якщо послідовність {хn} у метричному просторі має границю, то ця послідовність обмежена.
Доведення. Дійсно, якщо послідовність має границю, то це означає, що 

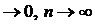 . Але
. Але 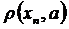 – числова послідовність і вона має границю рівну нулю, отже обмежена, тобто існує М, що
– числова послідовність і вона має границю рівну нулю, отже обмежена, тобто існує М, що 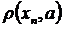
 , що і означає обмеженість, бо всі елементи послідовності знаходяться всередині кулі з центром в точці а і радіусом М.
, що і означає обмеженість, бо всі елементи послідовності знаходяться всередині кулі з центром в точці а і радіусом М.
Означення. Послідовність {хn} з метричного простору (Х,ρ) називається фундаментальною або послідовністю Коші, або збіжною в собі, якщо для 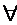 ε>0
ε>0  що як тільки n,m >N, то
що як тільки n,m >N, то 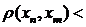 ε.
ε.
Теорема 3.  Якщо послідовність в метричному просторі має границю, то будь-яка її підпослідовність також має границю.
Якщо послідовність в метричному просторі має границю, то будь-яка її підпослідовність також має границю.
Теорема 4. Якщо послідовність має границю, то вона фундаментальна.
|
|
|
Доведення. Для  , і нехай
, і нехай 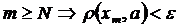
Оцінимо, 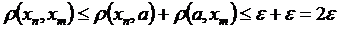 , а це і є умовою фундаментальності.
, а це і є умовою фундаментальності.
Теорему доведено.
Зауваження. Обернене твердження невірне, хоч для числових послідовностей воно справедливе.
Збіжність у метричних просторах.
Збіжність послідовностей у метричних просторах ще називається збіжністю за відстанню (якщо хn 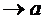 при
при  , то відстань між цими елементами прямує до нуля,
, то відстань між цими елементами прямує до нуля, 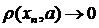 ). В кожному конкретному просторі цю збіжність можна охарактеризувати більш змістовно.
). В кожному конкретному просторі цю збіжність можна охарактеризувати більш змістовно.
Теорема 5. Для того, щоб послідовність 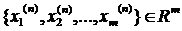 прямувала до граничного елемента а=(а1,а2,…,аm) необхідно і достатньо, щоб числові послідовності координат прямували до відповідних координат елемента а.
прямувала до граничного елемента а=(а1,а2,…,аm) необхідно і достатньо, щоб числові послідовності координат прямували до відповідних координат елемента а.
Доведення. Необхідність. Дано, що послідовність прямує до елемента а за відстанню. Це означає, що для 
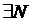 ,
,  то
то
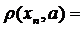
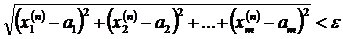 . Звідки випливає:
. Звідки випливає:
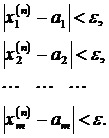
Зауважимо, що останні нерівності дістанемо, міркуючи від супротивного. Якби, наприклад, перший вираз був би меншим 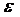 , то в квадраті він був би меншим
, то в квадраті він був би меншим 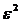 , отримали б суперечність. Останні нерівності означають, що:
, отримали б суперечність. Останні нерівності означають, що:
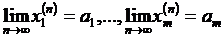 .
.
Необхідність доведено.
Достатність. Нехай числові послідовності координат мають границі. Тоді  :
:
 то
то 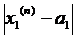 <ε ;
<ε ;
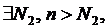 то
то 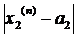 <ε ;
<ε ;
…. …. …. …. …. …. ….
|
|
|
 то
то 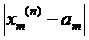 <ε ;
<ε ;
Візьмемо N=max{N1,N2,…,Nm}, тоді як тільки n>N, то всі нерівності виконуватимуться одночасно. Будемо мати:
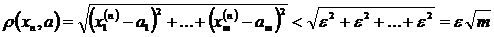 ,
, 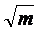 – стале.
– стале.
В силу довільного 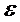 це означає, що відстань прямує до нуля, що і доводить достатність.
це означає, що відстань прямує до нуля, що і доводить достатність.
Теорему доведено.
У просторі Rm ми ввели такі три метрики: 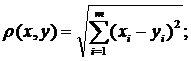

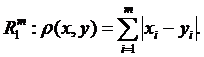
Теорема 6. У просторі Rm усі три метрики еквівалентні в тому розумінні, що із збіжності послідовності за однією метрикою випливає збіжність за двома іншими метриками.
Доведення. Розглянемо послідовність в просторі Rm 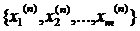 і нехай вона збігається за метрикою
і нехай вона збігається за метрикою 
 . Покажемо збіжність за двома іншими метриками:
. Покажемо збіжність за двома іншими метриками: 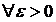
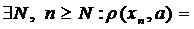
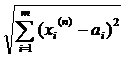 <ε, звідки випливає, що:
<ε, звідки випливає, що:  <ε2;
<ε2; 

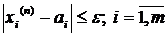 . Остання нерівність виконується для будь-якого і, тому і для максимуму:
. Остання нерівність виконується для будь-якого і, тому і для максимуму: 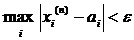 (отримали метрику в просторі R0m). Але тоді
(отримали метрику в просторі R0m). Але тоді 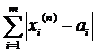 <ε+ε+…+ε=mε, що й доводить збіжність послідовності в простір R1m. Аналогічно доводяться два інші випадки.
<ε+ε+…+ε=mε, що й доводить збіжність послідовності в простір R1m. Аналогічно доводяться два інші випадки.
Теорему доведено.
Теорема 7. У просторі l2 із збіжності послідовності за відстанню випливає збіжність за координатами.
Доведення. a=(a1,a2,a3,…,am,…), 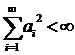 . Нехай маємо послідовність xn ={(x1(n), x2(n), … , xm(n),…)} і нехай ця послідовність збігається за відстанню.
. Нехай маємо послідовність xn ={(x1(n), x2(n), … , xm(n),…)} і нехай ця послідовність збігається за відстанню.

 ,
,
тоді 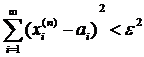 ;
; 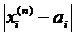 <ε для будь-якого i. Остання нерівність означає, що числові послідовності координат збігаються до відповідних координат елемента а.
<ε для будь-якого i. Остання нерівність означає, що числові послідовності координат збігаються до відповідних координат елемента а.
|
|
|
Зауваження. Обернене твердження не завжди справедливе, тобто із покоординатної збіжності не завжди випливає збіжність за відстанню.
Теорема 8. У просторі С[a,b] збіжність за відстанню рівносильна рівномірній збіжності.
Доведення. Нехай послідовність {xn(t)} 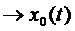 . Згідно метрики цього простору це означає, що
. Згідно метрики цього простору це означає, що 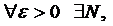
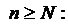
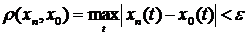 . Оскільки записана нерівність виконується при
. Оскільки записана нерівність виконується при 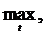 то вона буде виконуватись
то вона буде виконуватись 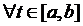 , тобто справедливою буде умова
, тобто справедливою буде умова 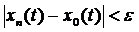 , а це є умовою рівномірної збіжності.
, а це є умовою рівномірної збіжності.
Нехай тепер послідовність функцій збігається до граничної функції рівномірно. Це означає, що  , то
, то  ,
,  , тоді це виконуватиметься і для
, тоді це виконуватиметься і для  <ε.
<ε.
Околи точок у метричному просторі та зв′язані з ними поняття.
Нехай маємо метричний простір (X,ρ).
Означення 1. Відкритою кулею з центром у точці x0 і радіусом R називається множина точок метричного простору, яка задовольняє нерівність 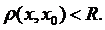 Якщо має місце, ще і рівність, то куля замкнена.
Якщо має місце, ще і рівність, то куля замкнена.
Приклад. Для простору R3 – це буде внутрішність сфери, дійсно 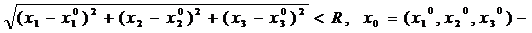 центр кулі, x=
центр кулі, x= 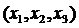 – біжучі координати. Для R2 кулею буде внутрішність круга радіуса R. Для R1 кулею буде інтервал. Для простору С[a,b] відкритою кулею буде смуга.
– біжучі координати. Для R2 кулею буде внутрішність круга радіуса R. Для R1 кулею буде інтервал. Для простору С[a,b] відкритою кулею буде смуга.
|
|
|
Означення 2. ε – околом точки х0називається відкрита куля з центром в точці х0і радіусом ε.
Означення 3. Точка х0називається точкою дотику множини Е, якщо в будь-якому її околі є принаймні одна точка множини.
Означення 4. Множина всіх точок дотику зветься замиканням множини E, і позначають [E].
Означення 5. Точка х0називається ізольованою точкою множини Е, якщо існує окіл цієї точки, який не містить жодної точки множини, окрім заданої.
Означення 6. Точка х0 зветься граничною точкою для множини Е, якщо в будь-якому її околі є нескінченна кількість точок множини Е.
Означення 7. Точка х0 називається внутрішньою точкою множини Е, якщо вона належить множині Е разом з деяким своїм околом.
Означення 8. Множина Е називається відкритою, якщо всі її точки внутрішні.
Означення 9. Множина Е називається замкненою, якщо вона містить всі свої граничні точки.
Означення 10. Множина СЕ називається доповненням множини Е до всього простору, якщо всі її точки належать простору і не належать множині Е.
Означення 11. Множина А називається щільною в множині В, якщо замикання А включає В ([A]  В).
В).
Означення 12. Множина А називається скрізь щільною, якщо її замикання співпадає з всім простором.
Якщо множина А щільна у всьому просторі, то будь-який елемент простору ми можемо як завгодно точно наблизити елементами множини А.
Означення 13. Метричний простір зветься сепарабельним, якщо він містить в собі зчисленну скрізь щільну підмножину.
Простір Rn – cепарабельний. Щільною підмножиною цього простору очевидно будуть все можливі набори n-раціональних чисел.
В теорії наближень функцій добре відома теорема Вейєрштрасса про те, що будь-яку неперервну функцію f(x) на сегменті  можна як завгодно точно наблизити алгебраїчним многочленом виду:
можна як завгодно точно наблизити алгебраїчним многочленом виду:
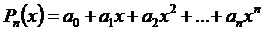 . Тобто
. Тобто  .
.
Щільною підмножиною у просторі С[a,b] буде множина алгебраїчних многочленів з раціональними коефіцієнтами. Ця множина зчисленна.
Теорема 9. Для того, щоб множина Е була відкритою, необхідно і достатньо, щоб її доповнення було замкненим.
Доведення. Необхідність. Дано множину Е, яка є відкритою, доведемо що СЕ замкнена, тобто містить всі свої граничні точки. Нехай точка х – гранична точка доповнення. Доведемо, що вона належить доповненню. Ця точка не може належати множині Е, бо якби належала, то разом з деяким своїм околом (так як Е – відкрита). А цього бути не може, оскільки в будь-якому околі х має знаходитись нескінчена кількість точок доповнення до Е. Необхідність доведена.
Достатність. Дано, що СЕ – замкнена. Доведемо, що Е – відкрита, тобто всі її точки внутрішні. Нехай x – деяка точка множини Е, вона не може бути граничною точкою доповнення (чому?), отже існує окіл, який не містить жодної точки доповнення, тоді цей окіл належить множині Е.
Теорему доведено.
Контрольні запитання.
1. Дати означення граничної точки, точки дотику, замикання множини.
2. Дати означення відкритої та замкненої множини.
3. Дати означення скрізь щільної множини та сепарабельного простору.
- Дати означення границі послідовності в метричному просторі, порівняти дане означення з означенням границі числової та векторної послідовностей
- Охарактеризувати збіжність послідовностей в просторі
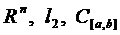
 .
.
Вправи.
1. Дано множину{0, 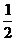 ,
,  ,…,
,…, 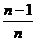 ,…}. Знайти граничні точки, точки дотику, межу та замикання даної множини.
,…}. Знайти граничні точки, точки дотику, межу та замикання даної множини.
2. Побудувати щільну підмножину в просторі 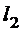 .
.
3. Довести сепарабельність простору С[a,b].
4. Довести, що з існування границі послідовності в довільному просторі випливає її обмеженість в цьому просторі.
Розв’язання.
1. Граничною точкою цієї множини буде точка 1, тому що в будь якому околі її є нескінченна кількість точок даної множини. Точками дотику будуть всі точки множини і точка 1. Ці точки складатимуть замикання і межу множини.
2. Такою підмножиною буде множина елементів із простору 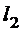 , у яких скінчена кількість перших координат відмінні від 0, а інші координати є нулі. Справді, кожен елемент із простору
, у яких скінчена кількість перших координат відмінні від 0, а інші координати є нулі. Справді, кожен елемент із простору 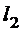 у цьому випадку ми можемо як завгодно точно наблизити елементом із щільної підмножини
у цьому випадку ми можемо як завгодно точно наблизити елементом із щільної підмножини  :
:
x={x 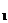 ,x
,x  ,x
,x 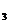 ,…,x
,…,x 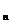 ..}
..} 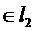 ,
, 
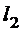 ,
,
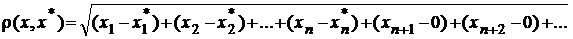 . Оскільки ряд
. Оскільки ряд  збіжний, то його залишок можна зробити як завгодно малим.
збіжний, то його залишок можна зробити як завгодно малим.
3. Щоб довести сепарабельність простору С[a,b] достатньо показати, що в цьому просторі існує замкнена скрізь щільна підмножина. За теоремою Вейєрштрасcа для будь-якої неперервної функції  , яка неперервна на сегменті
, яка неперервна на сегменті 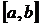 існує алгебраїчний многочлен степеня n який як завгодно точно наближає дану функцію. Тоді ясно, що можна підібрати алгебраїчний многочлен з раціональними координатами, який як завгодно точно наближатиме функцію
існує алгебраїчний многочлен степеня n який як завгодно точно наближає дану функцію. Тоді ясно, що можна підібрати алгебраїчний многочлен з раціональними координатами, який як завгодно точно наближатиме функцію 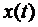 . Таких многочленів буде зчисленна множина. А це і доводить сепарабельність простору С[a,b].
. Таких многочленів буде зчисленна множина. А це і доводить сепарабельність простору С[a,b].
4. Маємо, що послідовність {xn} має границю в довільному метричному просторі (X, 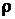 ). Це означає, що для будь-якого
). Це означає, що для будь-якого  , існує такий N, що при
, існує такий N, що при 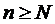 виконується нерівність
виконується нерівність 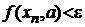 , тобто
, тобто  , коли
, коли  , але числова послідовність, яка має границю є обмеженою, тобто існує число
, але числова послідовність, яка має границю є обмеженою, тобто існує число 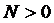 , що
, що 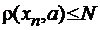 . Одержали, що всі члени послідовності знаходяться в абстрактній кулі з центром в точці a і радіусом N, що і доводить обмеженість даної послідовності.
. Одержали, що всі члени послідовності знаходяться в абстрактній кулі з центром в точці a і радіусом N, що і доводить обмеженість даної послідовності.
Задачі.
1. Дано множину  . Знайти граничні точки, точки дотику та замикання даної множини.
. Знайти граничні точки, точки дотику та замикання даної множини.
2. Навести приклади скрізь щільних множин, побудувати щільну підмножину в просторі l  .
.
3. Довести сепарабельність простору  .
.
4. Довести, що для того, щоб множина Е була відкрита, необхідно і достатньо, щоб її доповнення до всього простору було замкнене.
5. Довести, що збіжність за відстанню у просторах  рівносильна збіжності за координатами.
рівносильна збіжності за координатами.
6. Довести, що послідовність, яка має границю в довільному просторі є обмеженою.
7. Довести, що з існування границі послідовності в довільному просторі випливає її фундаментальність.
8. Довести, що три метрики в просторах 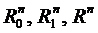 еквівалентні між собою.
еквівалентні між собою.
9. Записати околи точок у просторах R3, R2, R1, С[a,b] і зобразити їх на рисунку.
10. Побудувати абстрактну кулю більшого радіуса, яка міститься в середині кулі меншого радіуса.
11. Довести, що для того, щоб точка Х була граничною точкою необхідно і достатньо, щоб існувала послідовність Хn яка б прямувала до Х.
12. Дано М= 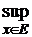 {x}. Довести що М – гранична точка множини Е.
{x}. Довести що М – гранична точка множини Е.
13. Довести, що послідовність 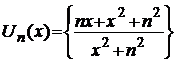 рівномірно збігається до U(x)=1 на сегменті
рівномірно збігається до U(x)=1 на сегменті 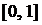 . Чи буде вона рівномірно збігатися по всій числовій осі.
. Чи буде вона рівномірно збігатися по всій числовій осі.
14. Дослідити на рівномірну збіжність {x 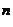 } для x
} для x 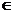
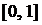 .
.
15. Довести теорему Больцано-Вейєрштрасса в просторах R3, R2.
16. Показати, що з рівномірної збіжності послідовності функцій {Х  (x)} випливає її збіжність за відстанню в просторі
(x)} випливає її збіжність за відстанню в просторі  . Чи справедливе обернене твердження?
. Чи справедливе обернене твердження?
17. Довести, що із збіжності послідовності за відстанню простору l  випливає покоординатна збіжність. Чи справедливе обернене твердження?
випливає покоординатна збіжність. Чи справедливе обернене твердження?
Дата добавления: 2018-04-15; просмотров: 1356; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
