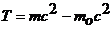Вопрос 5. Интервал между событиями.
Согласно классической механике пространство и время никак не связаны между собой. Пространственный интервал определяется разностями соответствующих координат: 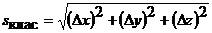 (пространственный интервал (отрезок) в классической механике).
(пространственный интервал (отрезок) в классической механике).
Согласно СТО пространство и время неразрывно связаны друг с другом. Иначе говоря, мир, в котором мы живем, является четырехмерным (3 координаты и время), поэтому вместо слова «отрезок» следует говорить «пространственно-временной интервал, включающий в себя кроме координат еще и время.
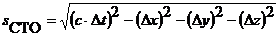 (пространственно-временной интервал в СТО).
(пространственно-временной интервал в СТО).
Пространственно-временной интервал sСТО является инвариантом при использовании преобразований Лоренца, т.е. имеет один и тот же вид в любой ИСО. Это можно показать, используя преобразования Лоренца (рекомендуем студентам проделать это самостоятельно для случая Dy=0, Dz = 0).
Вопрос 6. Релятивистский закон сложения скоростей.
Найдем скорость 1-го фотона в системе отсчета К¢, связанной со 2-ым фотоном, используя классическую формулу для сложения скоростей:
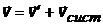
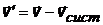
| классическая формула сложения скоростей в векторной форме |
|
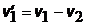
| -²- для 1-го фотона в проекциях, v1 –скорость 1-го в К, v¢1 – скорость 1-го в К¢, v2 – скорость 2-го, т.е. скорость К¢ в К. | |
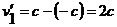
| Найдем v¢1 , учитывая, что v1 = v2 = с |
Таким образом, скорость одного фотона в системе отсчета, связанной со 2-ым, оказалась равной 2с, но согласно СТО ни одна частица не может двигаться со скоростью, большей скорости света.
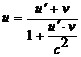
| релятивистская формула сложения скоростей u – скорость тела в неподвижной системе отсчета К, u¢ - скорость тела в движущейся системе отсчета К¢ , v – скорость системы К относительно системы К¢ |
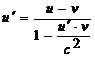
|
Вычислим теперь скорость фотона из предыдущего примера по релятивистской формуле.
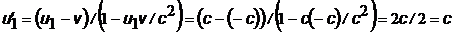
|
Вопрос 7. Кинетич. энергия релятивистской частицы. Энергия покоя. Полная энергия.
Найдем выражение для кинетической энергии в СТО, считая, что приращение кинетической энергии происходит за счет работы некоторой силы. Тело в начальный момент неподвижно и является свободным, т.е. не взаимодействует с другими телами и не обладает, таким образом, потенциальной энергией.
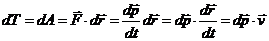 ¨ ¨
| чтобы проинтегрировать и получить | ||

| вместо переменной р появились переменные | ||
|
| здесь уже нет векторных произведений т.к. | ||
|
| возведем © в квадрат, выразим
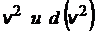 , подставим в § и получим , подставим в § и получим
| ||
|
| теперь можно проинтегрировать ¨, т.к. осталась одна переменная m | ||
|
| интегрируя, получим выражение для кинетической энергии в СТО | ||

| Релятивистская кинетическая энергия |

| энергия покоя |

| полная релятивистская энергия, т.е. энергия движущегося тела |

| При v<<c релятивистское выражение переходит в класи. |
Дата добавления: 2018-04-15; просмотров: 228; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

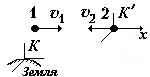
 , нужно свести к одной переменной m, пока их две
, нужно свести к одной переменной m, пока их две 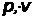 , и все равенства – скалярные произведения векторов,
, и все равенства – скалярные произведения векторов,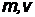
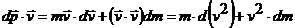 §
§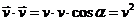 ,
, 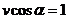 , но остались две переменные
, но остались две переменные 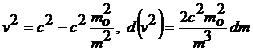
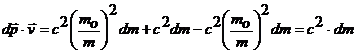
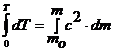 или
или