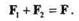Принцип независимости действия сил.

Дифференциальные уравнения движения

Материальной точки

Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от действия каждой силы в отдельности.

Пусть к материальной точке А приложены силы F₁и F₂, равнодействующая которых равна F. На основании аксиомы параллелограмма запишем

Разделим обе части равенства на массу точки, получим

откуда

Применяя последовательно аксиому параллелограмма, можно сказать, что при одновременном действии на материальную точку нескольких сил ее ускорение будет таким, как если бы действовала одна равнодействующая сила

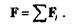
Пользуясь принципом независимости действия сил, выведем уравнение движения материальной точки в дифференциальной форме.

Пусть материальная точка А массой т движется в плоскости чертежа под действием силы F = F_i с ускорением а, тогда

Спроецируем это векторное равенство на две взаимно перпендикулярные оси координат х и у (оси и вектор силы F лежат в одной плоскости) и получим уравнения плоского движения материальной точки в координатной форме:

Применяя теорему о проекции ускорения на координатную ось, можно эти уравнения записать в виде дифференциальных уравнений плоского движения материальной точки:

126

В этих уравнениях X, Y — алгебраические суммы проекций сил,

действующих на точку, на соответствующие координатные оси; х и у — текущие координаты точки.

С помощью выведенных в этом параграфе уравнений решаются две основные задачи динамики: 1) по заданному движению точки определить действующие на нее силы; 2) зная действующие на точку силы, определить ее движение.

В тех случаях, когда при решении задач имеем дело с несвободной материальной точкой, необходимо применять принцип освобождаемости, т. е. отбросить связи и заменить их реакциями, учитывая последние в уравнениях движения наравне с действующими на точку активными силами.

Пример 13.1.Движение тела массой 0,5 кг выражается уравнениями

где х и у — в сантиметрах, t—в секундах. Определить силу, действующую на тело.

Решение. Данный пример относится к первой задаче динамики. Прежде всего, пользуясь теоремой о проекции ускорения на координатную ось, определим проекции ускорения на оси х и у:

Подставив эти значения в уравнения движения материальной точки, получим:

По проекциям силы, действующей на тело, видно, что она параллельна оси ординат, направлена в сторону отрицательных ординат и по модулю равна

Пример 13.2. Кривошип ОА длиной l, вращаясь равномерно с угловой скоростью 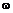, перемещает кулису, движущуюся поступательно вдоль направляющих I—I (рис. 13.1). Найти, пренебрегая трением, чему при этом равна сила давления F камня А на кулису, если сила тяжести ее равна G.

Решение. Данный пример относится к первой задаче динамики.

Применим принцип освобождаемости, отбросим связи кулисы и заменим их реакциями. Реакция N перпендикулярна направляющим кулисы, а сила давления F перпендикулярна кулисе, так как по условию трением пренебрегаем.

127

Кулиса движется возвратно-поступательно, следовательно, все ее точки движутся одинаково. Составим уравнение движения проекции точки А на ось х, которое и будет кинематическим уравнением движения кулисы:

Применив теорему о проекции ускорения на координатную ось, определим ускорение кулисы

Составим уравнение движения кулисы в координатной форме:

Спроецировав действующие накулису силы на осьд: и подставивзначения массы и ускорения, получим

откуда

Следовательно, сила давления ползуна на кулису изменяется пропорционально расстоянию кулисы от оси кривошипа.

Пример 13.3.На материальную точку массой 4 кг лежащую на гладкой горизонтальной плоскости действует горизонтальная сила F = 12 Н. С какой скоростью будет двигаться материальная точка через t = 10 с, если до приложения силы эта точка находилась в покое?

Решение. Данный пример относится ко второй задаче динамики.

Так как данная материальная точка лежит на гладкой горизонтальной плоскости, то под действием горизонтальной постоянной силы F точка будет двигаться прямолинейно равноускоренно. Направив ось дс вдоль траектории точки, запишем уравнение движения:

Спроецировав на ось х действующие на точку силы и подставив в это уравнение значение массы, определим ускорение

Применим формулу скорости равноускоренного движения

Подставив значения, получим

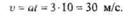
Пример 13.4. В результате полученного толчка кирпич начал скользить с начальной скоростью ₀ =2 м/с по неподвижной ленте конвейера, расположенного под углом = 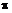/6 рад к горизонту. Определить перемещение s кирпича за про-

128

межуток времени t = 2с, если коэффициент трения скольжения кирпича о ленту конвейера f = 0,4; кирпич считать точечной массой (рис 13.2).

Решение. Данный пример относится ко второй задаче динамики. Выберем систему координат хОу таким образом, чтобы начало координат было в начальном положении тела, ось х была направлена вдоль ленты конвейера вниз, а ось у — перпендикулярно ленте конвейера вверх. Применив принцип освобождаемое, рассмотрим кирпич как материальную точку, движущуюся вдоль оси х под действием силы тяжести G, нормальной реакции N и силы трения F_тр.

Составим уравнения движения материальной точки:

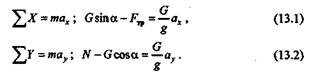
Кроме того, на основании второго закона трения скольжения можно записать

Так как материальная точка движется вдоль оси х, то а_у = 0, в результате чего из уравнения (13.2) имеем

Подставив это выражение в уравнение (13.3), получим

Полученное выражение подставим в уравнение (13.1):

Сокращая это равенство на G и учитывая, что а_х =а ,определим ускорение кирпича:

или, вынеся gcosa за скобку, получим

Так как правая часть этого равенства содержит только постоянные величины, то ускорение кирпича—величина постоянная, причем возможны три случая движения:

1) если tg > f, то а > 0 и движение будет равноускоренным;

2) если tg = f, тo a = 0 и движение будет равномерным;

3) если tg < f, то а < 0 и движение будет равнозамедленным.

129

Применив формулу пути равнопеременного движения, определим путь s, пройденный кирпичом за 2 с:

При данных в условии примера значениях tg > f, т. е. а > 0, следовательно, движение кирпича было равноускоренным.

Движение материальной точки,

Дата добавления: 2018-04-15; просмотров: 2298; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 27 28 29 30 313233 34 35 36 Следующая ⇒

Мы поможем в написании ваших работ!