Приложение двойных и тройных интегралов. (ВОПРОС 5)
1. Геометрический смысл двойного интеграла.Рассмотрим цилиндрическое тело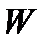 
с нижним основанием 
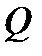, верхним основанием - поверхностью 
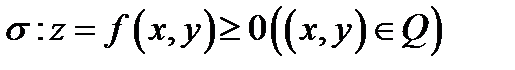и с образующей боковой поверхности, параллельной оси 
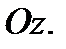Произведение 
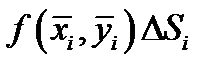есть объём цилиндра высоты 
и площадью основания 
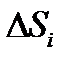, а интегральная сумма 
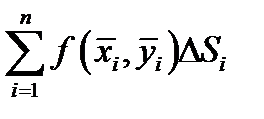– суть объём ступенчатого тела, построенного по разбиению 
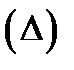. Ясно, что объём тела 
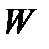приближенно равен объёму этого ступенчатого тела, т.е. 
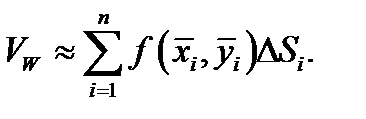Это равенство будет тем точнее, чем мельче разбиение 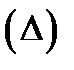, и при 
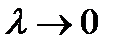оно становится точным, т.е. 
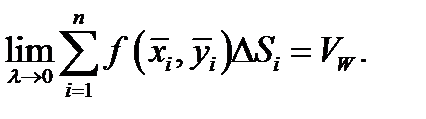Здесь слева стоит двойной интеграл 
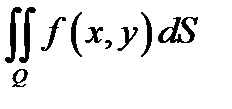, поэтому 
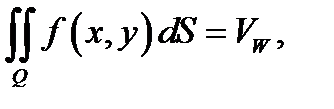т.е. двойной интеграл 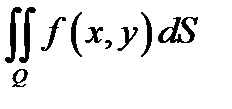равен объёму цилиндрического тела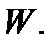 
2. Механический смысл тройного интеграла.Если 
плотность тела 
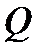в точке 
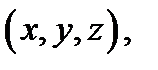то произведение 
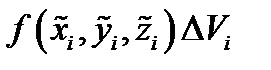приближенно равно массе тела 
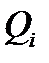, а интегральная сумма 
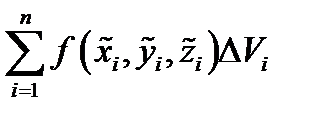приближенно равна массе всего тела 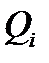, т.е. 
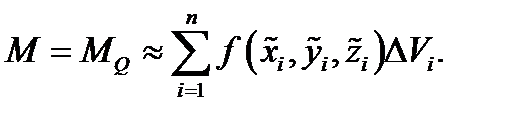Ясно, что это равенство будет тем точнее, чем мельче разбиение 
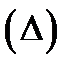, и при 
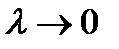оно становится точным: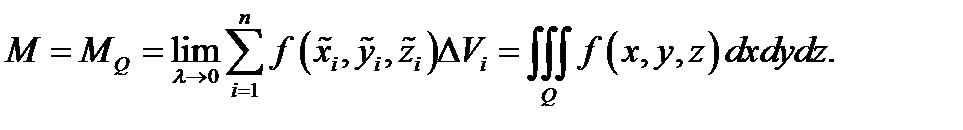 
Таким образом, тройной интеграл по телу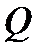 
от плотности 
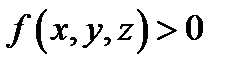равен массе тела 
3. Масса плоской пластинки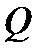 
с плотностью 
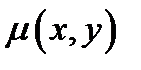в точке 
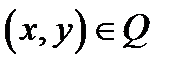вычисляется по формуле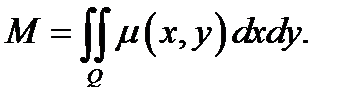 
4. Площадь плоской области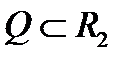 
можно вычислить по формуле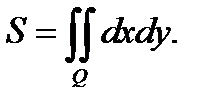 
5. Объём тела 
можно вычислить тройным интегралом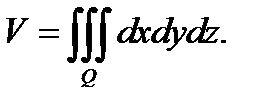 
6. Немного позже будет дано понятие площади произвольной поверхности. Будет показано, что если поверхность 
задана уравнением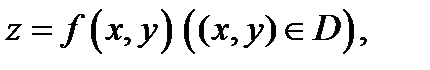 
то её площадь можно вычислить по формуле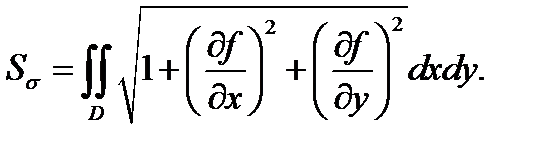 
6. Криволинейные интегралы. Определение и методы вычислений. (ВОПРОС 6)
|
|
|
Определение: Криволинейным интегралом первого типа от функции f(х, у, z) по кривой L называется предел интегральной суммы, который зависит ни от способа разбиения дуги , ни от выбора точек на дугах: при 
и max 
: 
.
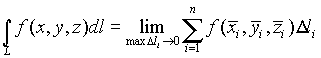Методы вычисления: вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла.1. Если пространственная кривая L задана параметрическими уравнениями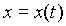 
, 
, 
, 
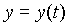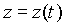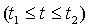,тогда криволинейный интеграл вычисляется по формуле 
.
2. Частный случай плоской кривой, заданной уравнением у=у(х), где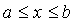 
имеем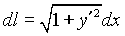 
,следовательно 
.
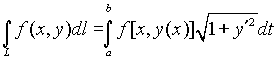3. Кривая заданная соотношением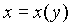 
,следовательно, имеем 
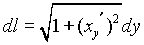и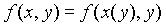 
,тогда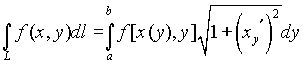 
4. Плоская кривая заданная уравнением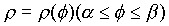 
в полярных координатах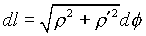, то 
, то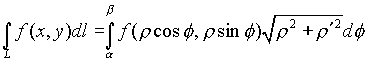 
.
Поверхностные интегралы. Определение и методы вычисления.(ВОПРОС7)
Определение: Если существует предел интегральных сумм: 
и если этот предел не зависит от вида разбиения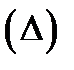 
и выбора точек 
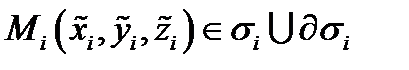, то его называют поверхностным интегралом первого рода от функции 
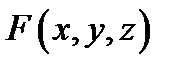по поверхности 
и обозначают 
Методы вычисления:Теорема 1. Если поверхность задана уравнением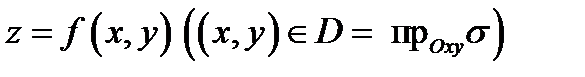 
и функции 
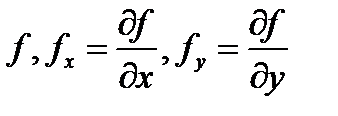непрерывны в замкнутой ограниченной области 
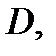а функция 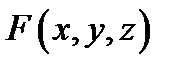непрерывна на поверхности 
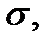то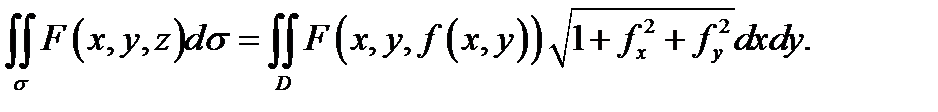 
|
|
|
Доказательствоследует из равенства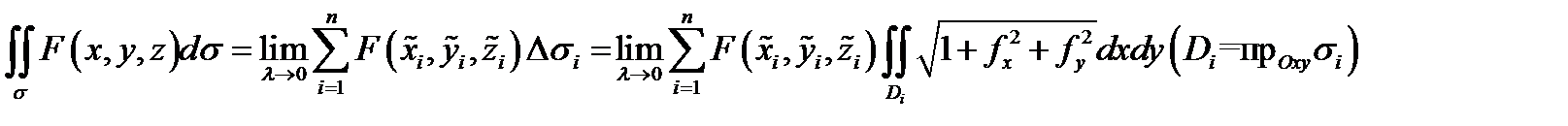 
и теоремы о среднем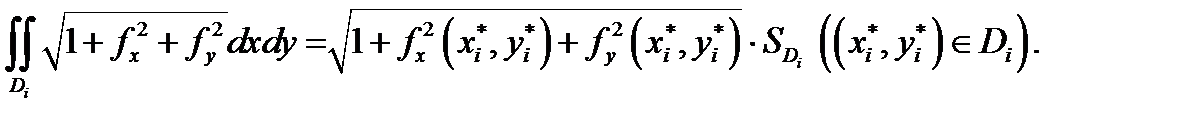 
Подставляя это в предыдущее равенство и учитывая непрерывность всех функций, будем иметь
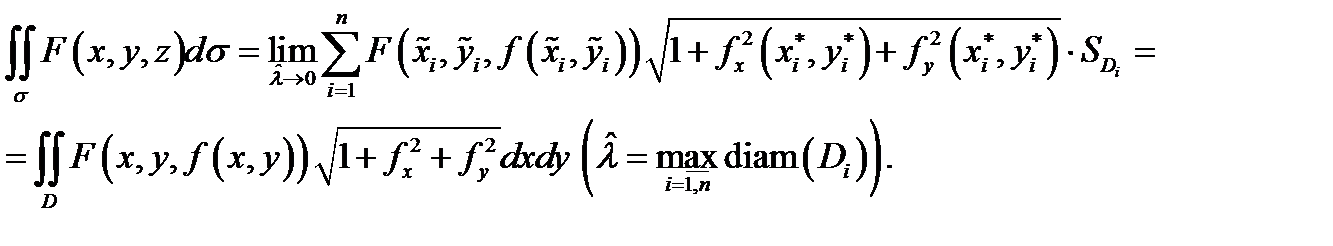
Теорема доказана. Так как поверхностный интеграл сводится к двойному, то для него справедливы все свойства двойного интеграла.
8. Векторное поле. Поток векторного поля. Случай замкнутой поверхности: формула Остроградского-Гаусса. Дивергенция векторного поля.(ВОПРОС 8)
Векторное поле - часть пространства, в каждой точкеM(x,y,z) которого задана векторная функция
Векторные линии - кривые, в каждой точке которых вектор поля направлен по касательной: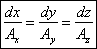 
Поток вектора α через поверхность σ - интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности: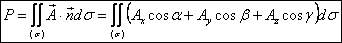 
Теорема Остроградского-Гаусса: Поток векторного поля A через замкнутую кусочно-гладкую поверхность S в направлении внешней нормали равен тройному интегралу от div A по области V, ограниченной поверхностью S :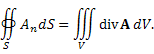 
.
Доказательство: Разобьём область V на малые элементы ΔV. Разбиение области V, ограниченной поверхностью S, на малые элементы ΔVk , границами которых являются поверхности ΔSk . Согласно определению дивергенции векторного поля, поток ΔΦk поля A через поверхность ΔSk малой области ΔVk можно представить в виде приближенного равенства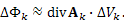 
Далее выполним суммирование по всем элементам области V и осуществим предельный переход, переходя к бесконечно малым элементам. Согласно свойствам потока векторного поля, сумма потоков из всех частей объема V равна потоку вектора A через внешнюю поверхность S: 
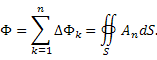. Сумма произведений 
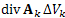по всем элементам разбиения области V представляет собой интегральную сумму от div A по этой области и, следовательно, 
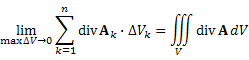,таким образом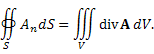 
(замкнутая поверхность).
|
|
|
Дивергенция вектора α - скаляр, равный объемной плотности потока в рассматриваемой точке поля: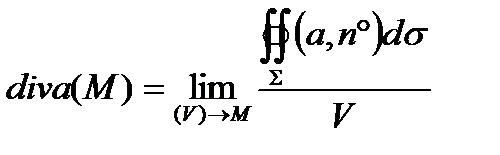 
,где σ - замкнутая поверхность, ограничивающая объем V; n° - орт ее внешней нормали; объем V->0 стягивается к рассматриваемой точке.
9. Работа векторного плоского поля: формула Грина как частный случай теоремы Остроградского-Гаусса. (ВОПРОС 9)
Работа векторного плоского поля-криволинейный интеграл 2 рода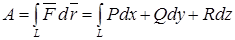 
.
Теорема: Пусть функции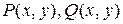 
и их частные производные непрерывны в области 
с положительно ориентированной границей 
Тогда имеет место следующая формула Грина: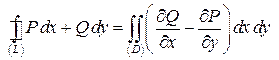 
. Доказательство проведем для области 
описываемой неравенствами 
.Сначала проверим равенство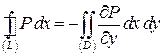 
.Сведем криволинейный интеграл 
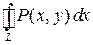к определенному интегралу, подставляя 
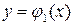на линии 
и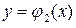 
и на линии 
: 
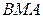.Теперь преобразуем двойной интеграл, сведя его сначала к повторному, а затем к определенному интегралу: 
.И криволинейный, и двойной интегралы равны одному и тому же определенному интегралу и, следовательно, равны между собой. Аналогично проверяется равенство: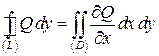 
.Складывая равенства, получим формулу Грина.
|
|
|
10. Циркуляция и ротор векторного поля. Теорема Стокса.(ВОПРОС 10)
Циркуляция векторного поля – это скалярная величина, которая является интегральной характеристикой поля; она указывает на способность векторного поля совершать работу при перемещении по замкнутым траекториям.
Циркуляцией вектора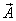 
по замкнутому контуру 
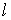называется работа этого векторного поля вдоль замкнутой кривой 
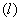, на которой указано направление обхода: 
.
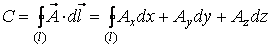Ротор вектора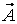 
в точке M – это вектор, проекция которого на каждое направление 
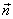равна пределу отношения циркуляции вектора 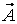по контуру 
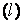плоской площадки S, перпендикулярной этому направлению, к площади этой площадки, стягивающейся в точку.
Циркуляция связана с ротором с помощью формулы Стокса: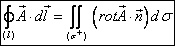 
.Смысл формулы Стокса теперь легко прочитывается:
Дата добавления: 2018-04-15; просмотров: 307; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!