Основы теории вероятностей и математической статистики.
1). Три стрелка производят по одному выстрелу в цель независимо друг от друга. Вероятности попадания в цель для каждого из них равны соответственно 0,7; 0,8; 0,9. Найти вероятность того, что: а) в цель попадет только один стрелок; б) в цель попадут только два стрелка; в) в цель попадет хотя бы один стрелок.
Решение.
а) Рассмотрим следующие события:
А1 - первый стрелок попал в цель;
А2 - второй стрелок попал в цель;
А3 - третий стрелок попал в цель;
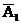 - первый стрелок не попал в цель;
- первый стрелок не попал в цель;
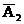 - второй стрелок не попал в цель;
- второй стрелок не попал в цель;
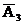 - третий стрелок не попал в цель.
- третий стрелок не попал в цель.
По условию Р(А1) = 0,7; Р(А2) = 0,8; Р(А3) = 0,9; Р( 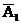 )=1 - 0,7 = 0,3; Р(
)=1 - 0,7 = 0,3; Р( 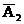 ) = 0,2; Р(
) = 0,2; Р( 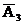 ) = 0,1.
) = 0,1.
Пусть событие В - попал только один стрелок. Тогда
В = А1 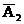
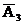 +
+ 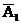 А2
А2 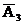 +
+ 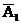
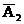 А3
А3
Отсюда в силу несовместимости событий-слагаемых и независимости событий-сомножителей.
Р(В)=Р(А1)Р( 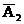 )Р(
)Р( 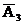 )+Р(
)+Р( 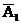 )Р(А2)Р(
)Р(А2)Р( 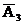 )+Р(
)+Р( 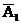 )Р(
)Р( 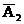 )Р(А3)=
)Р(А3)=
= 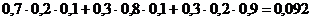
б) Пусть событие С - попадут только два стрелка. Тогда
С = А1А2 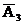 +А1
+А1 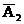 А3+
А3+ 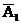 А2А3
А2А3
Отсюда

в) Пусть событие D - попал хотя бы один стрелок. Тогда противоположное событие 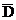 - не попал ни один из них, т.е.
- не попал ни один из них, т.е. 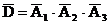 . Поэтому Р(
. Поэтому Р( 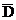 )=
)= 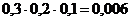 .
.
Отсюда
Р(D)=1 - Р( 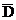 ) = 1 - 0,006 = 0,994.
) = 1 - 0,006 = 0,994.
2). Среди 15 микрокалькуляторов, имеющихся в вычислительной лаборатории, лишь 6 новых, а остальные - бывшие в употреблении. Наугад взято три микрокалькулятора. Какова вероятность, что все они окажутся новыми?
Решение.
Рассмотрим события:
А - первый из взятых микрокалькуляторов новый;
В - второй микрокалькулятор новый;
С - третий микрокалькулятор новый.
|
|
|
Тогда 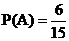 .
.
Вероятность того, что второй микрокалькулятор будет новый, при условии, что первым уже был отобран новый микрокалькулятор, т.е. условная вероятность события В, равна
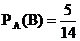
Вероятность того, что третьим будет отобранный микрокалькулятор, при условии, что уже отобраны два новых микрокалькулятора, т.е. условная вероятность события С, равна
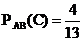
Искомая вероятность того, что все три отобранных микрокалькулятора окажутся новыми, равна
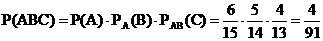
3). Заданы законы распределения двух независимых случайных величин Х и У.
| X | -5 | 2 | 3 | 4 |
| Y | 1 | 4 |
| P | 0,4 | 0,3 | 0,1 | 0,2 | P | 0,2 | 0,8 |
Найти математическое ожидание и дисперсию для случайной величины
Z = 3X - 2Y
Решение. Найдем математические ожидания и дисперсии для случайных величин Х и У.
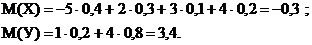
Напишем законы распределения для случайных величин Х2 и У2:
| X2 | 25 | 4 | 9 | 16 |
| Y2 | 1 | 16 |
| P | 0,4 | 0,3 | 0,1 | 0,2 | P | 0,2 | 0,8 |
Найдем математические ожидания для случайных величин Х2 и У2:
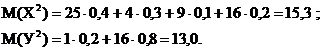
Отсюда
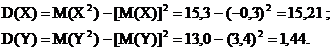
Наконец, пользуясь свойствами математического ожидания и дисперсии, а также независимостью случайных величин Х и У, получаем:
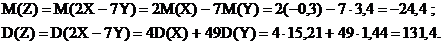
Текст задач. Варианты №1-30.
Раздел 1. Математический анализ
|
|
|
Задание №1. Найти пределы:
| № | Варианты заданий |
| 1 | 1. 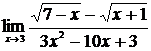 , ,
|
2. 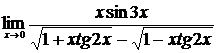 , ,
| |
3. 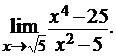
| |
| 2 | 1. 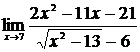 , ,
|
2. 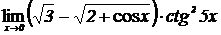
| |
3. 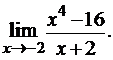
| |
| 3. | 1. 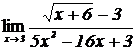
|
2.  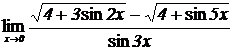
| |
3. 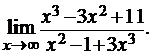
| |
| 4. | 1. 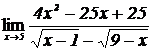
|
2. 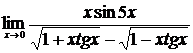 , ,
| |
3. 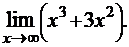
| |
| 5 | 1. 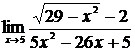 , ,
|
2. 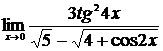 , ,
| |
3. 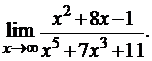
|
| 6 | 1. 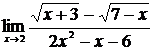 , ,
|
2. 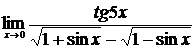 , ,
| |
3. 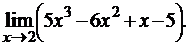
| |
| 7 | 1.  , ,
|
2.  , ,
| |
3. 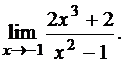
| |
| 8 | 1. 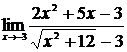 , ,
|
2. 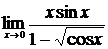 , ,
| |
3. 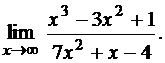
| |
| 9 | 1.  , ,
|
2. 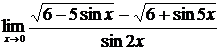 , ,
| |
3. 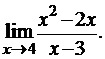
| |
| 10 | 1. 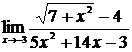 , ,
|
2. 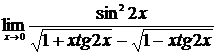 , ,
| |
3. 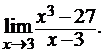
| |
| 11 | 1. 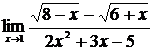 , ,
|
2. 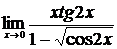 , ,
| |
3. 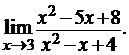
| |
| 12 | 1. 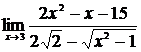 , ,
|
2. 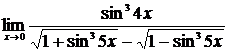 , ,
| |
3. 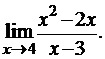
| |
| 13 | 1. 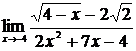 , ,
|
2. 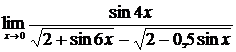 , ,
| |
3. 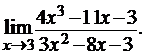
| |
| 14 | 1. 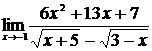 , ,
|
2. 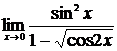 , ,
| |
3. 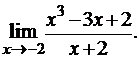
| |
| 15 | 1. 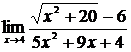 , ,
|
2.  , ,
| |
3. 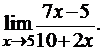
| |
| 16 | 1. 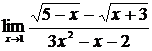 , ,
|
2. 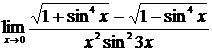 , ,
| |
3. 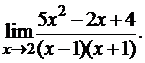
| |
| 17 | 1. 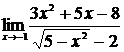 , ,
|
2. 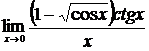 , ,
| |
3. 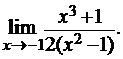
|
| 18 | 1. 
|
2. 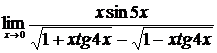
| |
3. 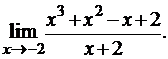
| |
| 19 | 1. 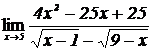
|
2. 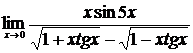 , ,
| |
3. 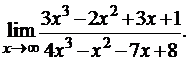
| |
| 20 | 1. 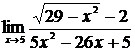 , ,
|
2. 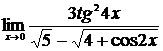 , ,
| |
3. 
| |
| 21 | 1. 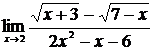 , ,
|
2. 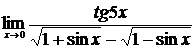 , ,
| |
3. 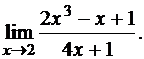
| |
| 22 | 1.  , ,
|
2.  , ,
| |
3. 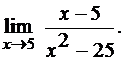
| |
| 23 | 1. 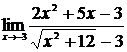 , ,
|
2. 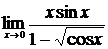 , ,
| |
3. 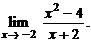
| |
| 24 | 1. 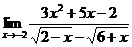 , ,
|
2. 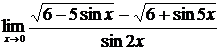 , ,
| |
3. 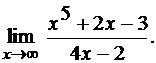
| |
| 25 | 1. 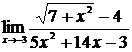 , ,
|
2. 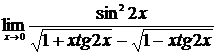 , ,
| |
3. 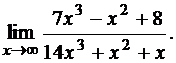
| |
| 26 | 1. 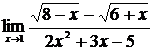 , ,
|
2. 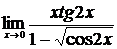 , ,
| |
3. 
| |
| 27 | 1. 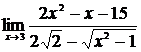 , ,
|
2. 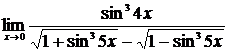 , ,
| |
3. 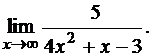
| |
| 28 | 1. 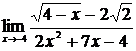 , ,
|
2. 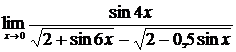 , ,
| |
3. 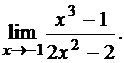
| |
| 29 | 1. 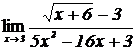
|
2.  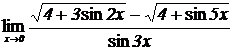
| |
3. 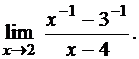
| |
| 30 | 1. 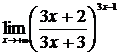 , ,
|
2. 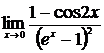
| |
3. 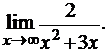
|
Задание №2. Найти производные указанных функций, используя правила дифференцирования:
| № | Варианты заданий | ||
| 1. | 1. 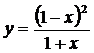 , ,
| ||
2. 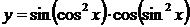 , ,
| |||
| 2. | 1. 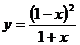 , ,
| ||
2.  , ,
| |||
| 3. | 1. 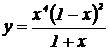 , ,
| ||
2.  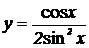 , ,
| |||
| 4. | 1. 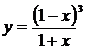 , ,
| ||
2. 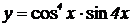 , ,
| |||
| 5. | 1. 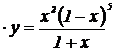 , ,
| ||
2.  , ,
| |||
| 6. | 1. 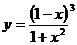 , ,
| ||
2.  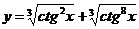 , ,
| |||
| 7. | 1. 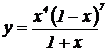 , ,
| ||
2. 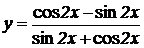 , ,
| |||
| 8. | 1.  , ,
| ||
2. 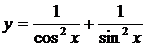 , ,
| |||
| 9. | 1. 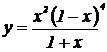 , ,
| ||
2. 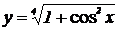 , ,
| |||
| 10. | 1. 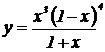 , ,
| ||
2.  , ,
| |||
| 11. | 1. 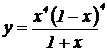 , ,
| ||
2. 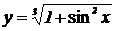 , ,
| |||
| 12. | 1. 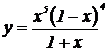 , ,
| ||
2. 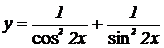 , ,
| |||
| 13. | 1. 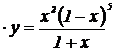 , ,
| ||
2. 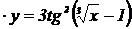 , ,
| |||
| 14. | 1. 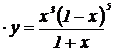 , ,
| ||
2. 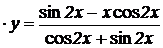 , ,
| |||
| 15. | 1. 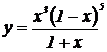 , ,
| ||
2.   , ,
| |||
| 16. | 1. 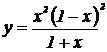 , ,
| ||
2. 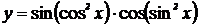 , ,
| |||
| 17. | 1. 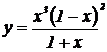 , ,
| ||
2.  , ,
| |||
| 18.
| 1. 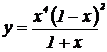 , ,
| ||
2.  , ,
| |||
| 19. | 1. 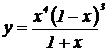 , ,
| ||
2. 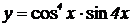 , ,
| |||
| 20. | 1. 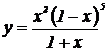 , ,
| ||
2. 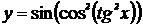 , ,
| |||
| 21. | 1. 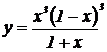 , ,
| ||
2. 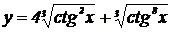 , ,
| |||
| 22. | 1. 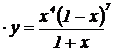 , ,
| ||
2. 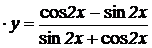 , ,
| |||
| 23. | 1.  , ,
| ||
2. 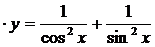 , ,
| |||
| 24. | 1. 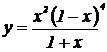 , ,
| ||
2.  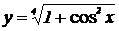 , ,
| |||
| 25. | 1. 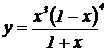 , ,
| ||
2.  , ,
| |||
| 26. | 1. 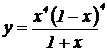 , ,
| ||
2. 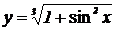 , ,
| |||
| 27. | 1. 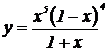 , ,
| ||
2. 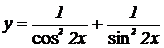 , ,
| |||
| 28. | 1. 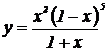 , ,
| ||
2. 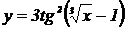 , ,
| |||
| 29. | 1. 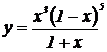 , ,
| ||
2. 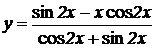 , ,
| |||
| 30. | 1. 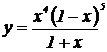 , ,
| ||
2. 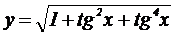 , ,
|
Задание № 3. Найти интегралы:
| № варианта | Текст задания
 Мы поможем в написании ваших работ! | |||
