Проверка статистических гипотез
Если закон распределения неизвестен, то выдвигают гипотезу о его виде. Возможен также случай, когда закон распределения известен, а его параметр 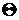 неизвестен. Тогда есть основание предположить, что неизвестный параметр
неизвестен. Тогда есть основание предположить, что неизвестный параметр 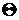 равен определённому значению
равен определённому значению 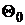 и выдвигают гипотезу
и выдвигают гипотезу 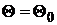 .
.
Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. гипотезы бывают простые и сложные.
Простой называют гипотезу, содержащую только одно предположение. Сложная гипотеза состоит из конечного числа простых гипотез.
Выдвинутая гипотеза называется нулевой и обозначается 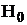 , а гипотеза, противоречащая нулевой – конкурирующей и обозначается
, а гипотеза, противоречащая нулевой – конкурирующей и обозначается 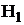 .
.
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость её проверки. В результате проверки могут быть допущены ошибки двух видов.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза, ошибка второго рода – будет принята неправильная гипотеза.
Решение признать верной гипотезу 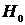 или
или  принимается по значению некоторой функции выборки, называемой статистическим критерием.
принимается по значению некоторой функции выборки, называемой статистическим критерием.
Значение критерия, вычисленное по выборке, называется наблюдаемым и обозначается 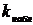 . Множество значений критерия можно разделить на два непересекающихся подмножества: подмножество значений критерия, при которых гипотеза
. Множество значений критерия можно разделить на два непересекающихся подмножества: подмножество значений критерия, при которых гипотеза 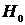 принимается, называется допустимой областью; подмножество значений критерия, при которых гипотеза
принимается, называется допустимой областью; подмножество значений критерия, при которых гипотеза 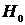 отвергается и принимается гипотеза
отвергается и принимается гипотеза  , называется критической областью.
, называется критической областью.
|
|
|
Критическими точками называются точки, отделяющие критическую область от допустимой. Эти точки являются табличными или критическими значениями критерия и обозначаются 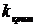 .
.
При проверке гипотез следует по возможности уменьшить вероятности принятия неправильных решений. Допустимая вероятность ошибки I рода 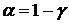 называется уровнем значимости.
называется уровнем значимости.
Для определения критической области используют уровень значимости и учитывают вид альтернативной гипотезы  .
.
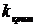 определяют по таблицам распределения данного критерия если
определяют по таблицам распределения данного критерия если  , то гипотеза
, то гипотеза 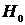 принимается, если
принимается, если  , то принимается гипотеза
, то принимается гипотеза  .
.
Пример решения задания 5
Для заданного интервального ряда выборки проверить гипотезу: закон распределения генеральной совокупности является нормальным.
| Интервал | 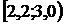
| 
| 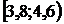
| 
| 
| 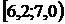
| 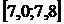
|
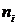
| 5 | 10 | 35 | 20 | 15 | 8 | 7 |
Решение
Выдвигаются нулевая и конкурирующая гипотезы:
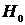 : закон распределения генеральной совокупности является нормальным;
: закон распределения генеральной совокупности является нормальным;
 : генеральная совокупность имеет закон распределения отличный от нормального.
: генеральная совокупность имеет закон распределения отличный от нормального.
Интервальный вариационный ряд преобразуется в дискретный. Для этого интервалы заменяются соответствующими им серединами, а частоты остаются прежними.
|
|
|
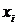
| 2,6 | 3,4 | 4,2 | 5,0 | 5,8 | 6,6 | 7,4 |
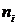
| 5 | 10 | 35 | 20 | 15 | 8 | 7 |
По полученным данным находятся выборочное среднее и выборочное среднеквадратическое отклонение.
1)  ;
;
2) 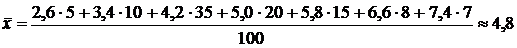 ;
;
3) 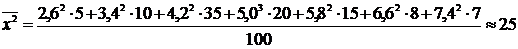 ;
;
4)  ;
;
5) 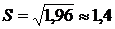 .
.
Гипотеза проверяется с помощью случайной величины 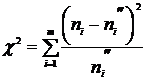 , число степеней свободы которой находится по формуле:
, число степеней свободы которой находится по формуле:
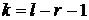 ,
,
где 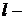 число интервалов, на которые разбит вариационный ряд;
число интервалов, на которые разбит вариационный ряд;
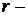 число параметров распределения, которые оценены по данным выборки (для нормального распределения
число параметров распределения, которые оценены по данным выборки (для нормального распределения 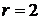 , для распределения Пуассона
, для распределения Пуассона 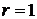 ).
).
Значит 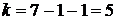 . Задаётся уровень значимости
. Задаётся уровень значимости 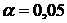 .
.
По уровню значимости и числу степеней свободы критическая точка правосторонней критической области 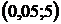 находится из приложения 5 [1, 2] и равна
находится из приложения 5 [1, 2] и равна 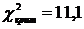 .
.
Предварительно определим теоретические частоты по формуле 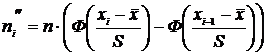 .
.
Расчёты представлены в таблице.
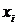
| 3,0 | 3,8 | 4,6 | 5,4 | 6,2 | 7,0 | 7,8 |
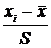
| –1,28 | –0,71 | –0,14 | 0,43 | 1,00 | 1,57 | 2,14 |
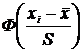
| –0,3997 | –0,2611 | –0,0557 | 0,1664 | 0,3413 | 0,4418 | 0,4838 |
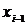
| 2,2 | 3,0 | 3,8 | 4,6 | 5,4 | 6,2 | 7,0 |
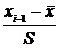
| –1,86 | –1,28 | –0,71 | –0,14 | 0,43 | 1,00 | 1,57 |
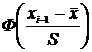
| –0,4686 | –0,3997 | –0,2611 | –0,0557 | 0,1664 | 0,3413 | 0,4418 |
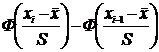
| 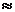 0,07 0,07
| 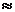 0,13 0,13
| 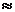 0,21 0,21
| 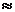 0,23 0,23
| 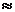 0,18 0,18
| 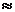 0,13 0,13
| 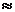 0,05 0,05
|
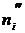
| 7 | 13 | 21 | 23 | 18 | 13 | 5 |
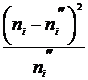
| 0,571 | 0,692 | 9,333 | 0,391 | 0,500 | 1,923 | 0,800 |
|
|
|
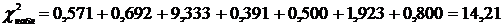
По уровню значимости и числу степеней свободы критическая точка правосторонней критической области 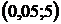 находится из приложения 5 [1, 2] и равна
находится из приложения 5 [1, 2] и равна 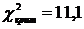 .
.
Так как 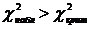 , то гипотеза
, то гипотеза 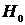 о нормальном распределении отвергается.
о нормальном распределении отвергается.
Ответ: закон распределения генеральной совокупности не является нормальным.
Дата добавления: 2018-04-15; просмотров: 192; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
