СИММЕТРИЧНЫЕ ДВОЙСТВЕННЫЕ ЗАДАЧИ
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
"Ижевский государственный технический университет имени М.Т.Калашникова"
(ФГБОУ ВПО «ИжГТУ имени М.Т.Калашникова»)
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторной работы
по дисциплинам «Теория принятия решений»,
«Системный анализ»
на тему «Двойственная задача в линейном программировании»
Рекомендовано советом факультета «Информатика и вычислительная техника» к использованию в качестве учебно - методических материалов для студентов
специальности: 230102.65 «Автоматизированные системы обработки информации и управления»,
специальности: 031301.65 «Теоретическая и прикладная лингвистика»
направления: 230100.62 «Информатика и вычислительная техника» в области: «Автоматизированные системы обработки информации и управления», «Системы автоматизированного проектирования»,
форма обучения: очная, заочная
(протокол № 8 от 22.11.2013 )
Ижевск 2013
Рецензент: Мокроусов М.Н., к.т.н., доцент кафедры АСОИУ.
Составители: Исенбаева Е.Н., старший преподаватель кафедры АСОИУ.
Рекомендовано советом факультета «Информатика и вычислительная техника» к использованию в качестве учебно- методических материалов для студентов специальности 230102.65 «Автоматизированные системы обработки информации и управления», специальности 031301.65 «Теоретическая и прикладная лингвистика», направления: 230100.62 «Информатика и вычислительная техника» в области: «Автоматизированные системы обработки информации и управления», «Системы автоматизированного проектирования».
|
|
|
(протокол № 8 от 22.11.2013 ).
Методические указания к выполнению лабораторной работы на тему «Двойственная задача в линейном программировании» (теория и варианты заданий) / сост. Е.Н. Исенбаева.- Ижевск, 20013 г.- 26 с.
В методических указаниях рассматривается проблема двойственности в линейном программировании. Рассмотрен экономический смысл двойственности, описаны алгоритмы построения двойственных задач для симметричной прямой задачи и прямой задачи в общей постановке. Разобраны основные теоремы двойственности. Приведены реализации указанных алгоритмов. Методические указания содержат варианты заданий для практических занятий.
Учебное пособие предназначено для студентов, обучающихся по специальности 230102.65 «Автоматизированные системы обработки информации и управления», специальности 031301.65 «Теоретическая и прикладная лингвистика», по направлению 230100.62 «Информатика и вычислительная техника» в области: «Автоматизированные системы обработки информации и управления», «Системы автоматизированного проектирования» очной и заочной формы обучения.
|
|
|
© Исенбаева Е.Н., составление, 20013
© ФГБОУ ВПО «ИжГТУ имени М.Т. Калашникова, 2013
СОДЕРЖАНИЕ
1. ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ.. 3
2. СИММЕТРИЧНЫЕ ДВОЙСТВЕННЫЕ ЗАДАЧИ.. 3
3. ОБЩИЙ СЛУЧАЙ ДВОЙСТВЕННОСТИ.. 3
4. ДВОЙСТВЕННЫЙ СИМПЛЕКСНЫЙ МЕТОД (СМ) 3
5. ВАРИАНТЫ ЗАДАНИЙ.. 3
СПИСОК ЛИТЕРАТУРЫ.. 3
ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
Любую задачу максимизации линейного программирования (ЛП) с экономической точки зрения можно рассматривать как задачу о распределении ограниченных ресурсов b1,b2,…,bm между различными потребителями, например, между некоторыми технологическими процессами, которые представляются столбцами A1,A2,…An матрицы ограничений задачи. Любое допустимое решение задачи ЛП x1,x2,…xn дает конкретное распределение, указывающее ту долю каждого из ресурсов, которая должна быть использована при осуществлении соответствующего технологического процесса.
|
|
|
Рассмотрим пример. Завод производит три вида продукции x1,x2 и x3, каждый из которых требует затрат времени на обработку на токарном, фрезерном и сверлильном станках. Количество машинного времени для каждого из станков ограничено. Пусть c1,c2,c3 – прибыль от реализации единицы соответствующего вида продукции. Необходимо определить, какое количество каждого вида продукции необходимо производить в течение недели, чтобы получить максимальную прибыль[1].
Формально эта задача записывается так:
максимизировать (c1x1+c2x2+c3x3) (1)
при ограничениях
a11x1+ a12x2+ a13x3 ≤ b1;
a21x1+ a22x2+ a23x3 ≤ b2;
a31x1+ a32x2+ a33x3 ≤ b3, (2)
где a1j, a2j, a3j – время, необходимое для обработки единицы j-го вида продукции соответственно на токарном, фрезерном и сверлильном станках (j= 1, 2, 3); b1, b2, b3 – недельный ресурс машинного времени соответственно для токарного, фрезерного и сверлильного станков.
Обозначим y1,y2 и y3 –цену единицы времени работы на токарном, фрезерном и сверлильном станках. Тогда a11y1+ a21y2+ a31y3 – можно трактовать как расходы на изготовление единицы продукции первого вида; a12y1+ a22y2+ a32y3 – расходы на изготовление единицы продукта второго вида и т. д.
|
|
|
Предположим, что цены ресурсов y1,y2,…,ym выбраны так, что выполняются следующие соотношения:
a11y1+ a21y2+ a31y3 ≥ с1;
a12y1+ a22y2+ a32y3 ≥ с2;
a13y1+ a23y2+ a33y3 ≥ с3. (3)
Поскольку b1, b2 и b3 – использованный ресурс машинного времени для каждого из станков, то b1y1+b2y2+ b3y3 – суммарные расходы на производство.
Требуется найти такие y1,y2 и y3, удовлетворяющие условиям (3), при которых минимизируются суммарные расходы на производство:
минимизировать g(y1 ,y2, y3)= b1y1+b2y2+ b3y3 (4)
при условиях
y1≥0; y2≥0; y3≥0.
Такую задачу называют двойственной задачей по отношению к задаче (1), называемой прямой.
СИММЕТРИЧНЫЕ ДВОЙСТВЕННЫЕ ЗАДАЧИ
Многие ЗЛП первоначально ставятся в прямых или двойственных задачах, поэтому имеет смысл говорить о паре двойственных задач линейного программирования.
Запишем теперь прямую и двойственную задачи в общем случае[2].
Прямая задача:
максимизировать
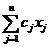 (5)
(5)
при условиях
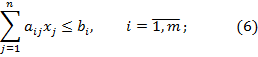
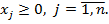 (7)
(7)
Двойственная задача:
минимизировать

при условиях
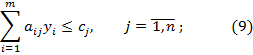
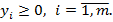 (10)
(10)
В матричном виде пара двойственных задач записывается следующим образом:
максимизировать сTx (11)
при условиях
Ax≤b; (12)
x≥0; (13)
минимизировать bTy (14)
при условиях
ATy≥c; (15)
y≥0. (16)
Сопоставляя формы записи прямой и двойственной задач, можно установить между ними следующие взаимосвязи:
1) если прямая задача является задачей максимизации, то двойственная будет задачей минимизации, и наоборот;
2) коэффициенты целевой функции прямой задачи c1,c2,…,cn становятся свободными членами ограничений двойственной задачи;
3) свободные члены ограничений прямой задачи b1,b2,…,bm становятся коэффициентами целевой функции двойственной задачи;
4) матрицу ограничений двойственной задачи получают транспонированием матрицы ограничений прямой задачи;
5) знаки неравенств в ограничениях изменяются на обратные;
6) число ограничений прямой задачи равно числу переменных двойственной задачи, а число ограничений двойственной задачи равно числу переменных прямой задачи.
Переменные y1,y2,…,ym двойственной задачи иногда называют теневыми ценами.
Двойственную задачу выгоднее решать, чем исходную прямую, если в прямой
задаче при малом количестве переменных имеется большое количество ограничений (m 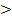 n).
n).
Пример.
Построить двойственную задачу к следующей задаче линейного программирования.
максимизировать
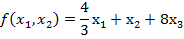
при ограничениях
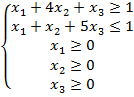
Прямая задача – задача на максимизацию, поэтому все ограничения должны иметь знак «≤». Для упорядочивания записи умножаем первое ограничение на (-1):
Получаем следующую систему ограничений.
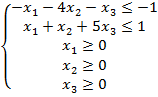
Двойственная задача записывается так:
минимизировать
z (y1,y2,y3)=-y1+y2
при ограничениях
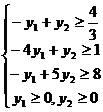
ТЕОРЕМЫ ДВОЙСТВЕННОСТИ
Связь между оптимальными решениями прямой и двойственной задач устанавливают посредством следующих теорем двойственности.
ТЕОРЕМА 1. Если 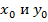 - допустимые решения прямой и двойственной задач, т. е.
- допустимые решения прямой и двойственной задач, т. е.  то
то
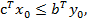 (17)
(17)
т.е. значения целевой функции прямой задачи никогда не превышают значения целевой функции двойственной задачи.
ТЕОРЕМА 2 (основная теорема двойственности). Если 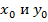 - допустимые решения прямой и двойственной задач и если
- допустимые решения прямой и двойственной задач и если 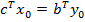 , то
, то 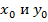 – оптимальные решения пары двойственных задач.
– оптимальные решения пары двойственных задач.
ТЕОРЕМА 3.Если в оптимальном решении прямой задачи (5) – (7) i-ое ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей двойственной переменной равно нулю, т. е.
если
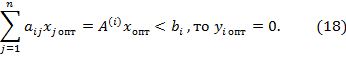
где  - i-ая строка матрицы А.
- i-ая строка матрицы А.
Смысл теоремы 3 состоит в следующем. Если некоторый ресурс  имеется в избытке и i-е ограничение при оптимальном решении выполняется как строгое неравенство, то оно становится несущественным, и оптимальная цена соответствующего ресурса равна 0.
имеется в избытке и i-е ограничение при оптимальном решении выполняется как строгое неравенство, то оно становится несущественным, и оптимальная цена соответствующего ресурса равна 0.
Теорему 3 дополняет теорема 4, устанавливающая взаимосвязь между оптимальным решением прямой задачи и ограничениями двойственной.
ТЕОРЕМА 4.Если в оптимальном решении двойственной задачи ограничение j выполняется как строгое неравенство, то оптимальное значение соответствующей переменной прямой задачи должно быть равно нулю, т. е. если 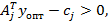 то
то
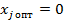 . (19)
. (19)
Дадим экономическую интерпретацию теоремы 4.
Поскольку величины 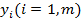 представляют собой цены соответствующих ресурсов, то
представляют собой цены соответствующих ресурсов, то
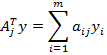
– это затраты на j-й технологический процесс, величина 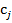 - прибыль от реализации на единицу изделия. Поэтому с экономической точки зрения теорема 2.7 означает следующее: если j-й технологический процесс оказывается строго невыгодным с точки зрения оптимальных цен ресурсов
- прибыль от реализации на единицу изделия. Поэтому с экономической точки зрения теорема 2.7 означает следующее: если j-й технологический процесс оказывается строго невыгодным с точки зрения оптимальных цен ресурсов 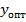 , то в оптимальном решении прямой задачи интенсивность данного технологического процесса должна быть равно 0.
, то в оптимальном решении прямой задачи интенсивность данного технологического процесса должна быть равно 0.
Таким образом, теорема 4 выражает принцип рентабельности оптимально организованного производства.
Из нее вытекает также, что 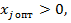 то
то
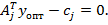 (20)
(20)
Предположим, что среди переменных x1,x2,…,xn прямой задачи есть множество из m переменных, которые в оптимальном решении имеют ненулевое значение. Пусть, например, таковыми оказались первые по порядку m переменных.
Тогда на основании уравнения (22) получают m условий рентабельности:
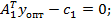
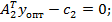 (21)
(21)
…
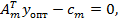
где 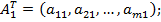
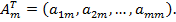
Приведем еще две важные теоремы теории двойственности.
ТЕОРЕМА 5 (теорема существования). Прямая и двойственная задачи имеют оптимальные решения тогда, и только тогда, когда обе они имеют допустимые решения.
ТЕОРЕМА 6 (теорема двойственности).Допустимый вектор x0 оптимален тогда, и только тогда, когда в двойственной задаче имеется такое допустимое решение y0 , что
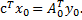 (22)
(22)
Между оптимальным решениями прямой и двойственной задачи, элементами индексных строк симплекс-таблиц, соответствующих этим решениям, существует следующая взаимосвязь:
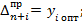
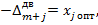 (23)
(23)
i=1, 2, …, m; j=1, 2, …, n,
где n – количество переменных прямой задачи; m – количество ее ограничений; 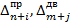 - соответствующие элементы индексной строки прямой и двойственной задач соответственно. При этом, если n+i, где 1 ≤ i ≤ m больше числа векторов-столбцов матрицы ограничений расширенной формы соответствующей задачи, то элементы
- соответствующие элементы индексной строки прямой и двойственной задач соответственно. При этом, если n+i, где 1 ≤ i ≤ m больше числа векторов-столбцов матрицы ограничений расширенной формы соответствующей задачи, то элементы 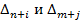 находятся путем циклической перестановки элементов индексной строки, начиная с элемента
находятся путем циклической перестановки элементов индексной строки, начиная с элемента 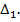
ОБЩИЙ СЛУЧАЙ ДВОЙСТВЕННОСТИ
В предыдущей главе были установлены основные соотношения для пары двойственных ЛП-задач при ограничениях в форме неравенств. Обобщим теперь эти результаты на случай произвольных ограничений.
Пусть прямая ЛП-задача задана в виде:
максимизировать

при условиях
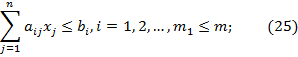

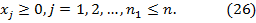
Тогда двойственная задача по отношению к (24)-(26) (или сопряженная с ней) состоит в минимизации линейной формы:
минимизировать
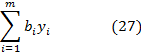
при условиях
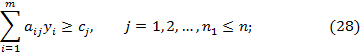

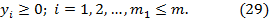
Таким образом, задача, сопряженная с задачей со смешанными условиями, составляется согласно следующим правилам:
1. Если переменная xj прямой задачи предполагается неотрицательной, то j-е условие системы ограничений (28) является неравенством.
2. Если на xj не накладывается такое ограничение, то j-е ограничение двойственной задачи будет равенством.
Аналогичным образом связаны знаки переменных двойственной задачи yi и соответствующие им ограничения прямой задачи. Заметим, что если положить m1=m и n1=n, то получим частный случай пары двойственных задач с ограничениями в форме неравенств.
Пример.
Построить двойственную задачу к следующей прямой задаче линейного программирования.
максимизировать
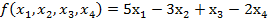
при ограничениях

Упорядочим запись ограничений, умножим третье ограничение на (-1):
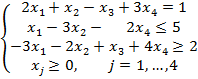
Получаем следующую двойственную задачу:
минимизировать
g(y1,y2,y3)=y1+5y2-2y3
при ограничениях

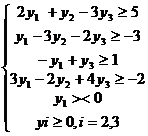
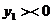 (не ограничена в знаке)
(не ограничена в знаке)
Дата добавления: 2018-04-15; просмотров: 667; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
