Формирование симплексной таблицы.
Все необходимые базисные решения целесообразно получить в так называемой таблице Гаусса. Сначала в эту таблицу заносятся исходные данные задачи. При необходимости некоторые уравнения системы ограничений следует умножать на –1, чтобы все свободные члены уравнений были неотрицательны.
Последнюю строку таблицы, часто называемую индексной, заполняем коэффициентами целевой функции, представленной в виде уравнения
 где с0 — свободный член L(X).
где с0 — свободный член L(X).
Алгоритм симплексного метода
1. Прежде всего, нужно привести систему ограничений к виду, где базисные переменные и целевая функция выражаются через свободные переменные. Тем самым мы найдем одно из неотрицательных базисных решений. Предположим, что в симплексной таблице получено такое решение.В данном примере каждое уравнение содержит переменную с коэффициентом, равным единице, которая во все остальные уравнения входит с коэффициентом, равным нулю. Это переменные x3, x4, x5 и x6. Они и являются базисными. Отсюда находим первое допустимое решение (или начальный опорный план): (0, 0, 19, 13, 15, 18).
Теорема. Если в индексной строке симплексной таблицы среди коэффициентов целевой функции нет положительных, то базисное решение является оптимальным и задача решена. К тому же, если в индексной строке, нет нулевых коэффициентов (не считая нулей, соответствующих базисным переменным), то решение единственное. В этом решении все небазисные переменные равны нулю, а базисные –– свободным членам. Если среди коэффициентов индексной строки имеются положительные, то значение целевой функции можно увеличить. Доказательство этой теоремы вытекает из приведенного выше исследования зависимости значения целевой функции от значения коэффициентов ее индексной строки в симплексной таблице.
2. Пусть в индексной строке имеются положительные коэффициенты. Просматриваем соответствующие столбцы коэффициентов. Если среди коэффициентов этих столбцов нет положительных, то задача решений не имеет. В противном случае можно перейти к другому базисному допустимому решению, более близкому к оптимальному.
3. Переход к другому базисному решению осуществляется элементарными так называемыми преобразованиями Жордана-Гаусса для строк таблицы. Они состоят в следующем: В индексной строке выбираем положительный (как правило, наибольший) коэффициент. Соответствующий столбец мы называем разрешающим. В рассматриваемом примере разрешающий столбец –– первый.
4. Предположим, что разрешающий столбец выбран. Составим отношения свободных членов уравнений (строка целевой функции здесь не участвует) к положительным коэффициентам разрешающего столбца (отрицательные его коэффициенты и нули не участвуют). Находим минимальное из этих отношений. Строку с этим числом надо считать разрешающей. Если таких строк несколько, то берем любую из них.
12. Поиск начального базисного допустимого решения задачи линейного программирования
. 
Решение. Задача задана в канонической форме (не надо вводить дополнительные переменные). Заполняем таблицу Гаусса и приступаем к поиску первого базисного допустимого решения.
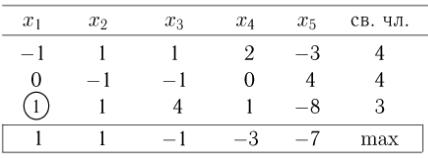
1) В качестве разрешающего берем первый столбец с положительным коэффициентом индексной строки (этот столбец наиболее простой, в нем уже имеем один нуль). Разрешающий коэффициент (в таблице он обведен кружком) берем в третьей строке (других вариантов нет).
Второй блок таблицы получим следующим образом:
а) разрешающая строка прибавляется к первой (получили первый нуль в разрешающем столбце);
б) вторая строка переписывается (она уже содержит нуль в разрешающем столбце);
в) разрешающая строка сохраняется (разрешающий коэффициент равен единице);
г) разрешающая строка, умноженная на –1, прибавляется к индексной (в которой находятся коэффициенты целевой функции).
Получен первый единичный столбец (столбец переменной х1)

В качестве разрешающего берем столбец с единственным положительным коэффициентом в индексной строке. Выбираем разрешающий коэффициент во второй строке (других вариантов нет) и обводим его кружком.
Заполняем третий блок таблицы Гаусса:
а) разрешающая строка делится на 4;
б) остальные коэффициенты пересчитываются по правилу прямоугольника.
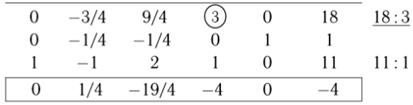
2) В базис нужно ввести x2, поскольку только при x2 коэффициент индексной строки положителен. С другой стороны, ввести x2 нельзя, потому что все коэффициенты этого столбца отрицательные — это приведет к недопустимому решению. Поэтому в базис ввели х4.
Заполняем четвертый блок таблицы Гаусса:

Получено первое базисное допустимое решение Х1 = (5, 0, 0, 6, 1). Это решение является оптимальным, так как в индексной строке нет положительных коэффициентов. Итак, оптимальное решение (5, 0, 0, 6, 1) получено одновременно с первым базисным решением. При этом Lmax = – 20.
Дата добавления: 2018-04-15; просмотров: 362; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
