Южно-Казахстанская государственная фармацевтическая академия
Кафедра медицинской биофизики, информатики и математики
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
Дисциплина: Биологическая статистика
Код дисциплины:Bio 3214
Специальность 5В110400 «Медико-профилактическое дело»
Практические занятия: 24 (часа)
Курс: 3
Семестр: 5
Учебный год
Обсуждено на заседании кафедры от «___»___________2014 г.
Протокол № ____
Зав. кафедрой _______________
Занятие №1
1. Тема: Введение в программу «Statistica». Создание, редактирование и сохранение таблиц исходных данных. Построение простейших графиков в программе «Statistica».
2. Цель: Знакомство с некоторыми возможностями программы «Statistica».
3. Задачи обучения:Научитьсоздавать, редактировать, сохранять таблицы исходных данных и строить простейшие графики в программе «Statistica».
4. Основные вопросы темы:
1. Из каких основных этапов состоит проведение статистического анализа в программе «Statistica»?
2. С какими типами документов работает программа «Statistica»? Какие расширения имеют эти документы?
3. Из каких элементов состоит основное рабочее окно программы «Statistica»?
4. Какие операции можно производить со столбцами и строками электронной таблицы? Какие команды при этом используют?
5. Как строятся простейшие графики в программе «Statistica»? Какие виды простейших графиков Вы знаете?
|
|
|
5. Методы обучения и преподавания: статистическая обработка данных с помощью компьютерной программы «Statistica 10».
v Задания:
1. Ознакомиться с краткой теорией практического занятия №1.
2. Выполнить примеры 1.1, 1.2, 1.3, 1.4.
3. В программе «Statistica 10» создать и самостоятельно заполнить таблицу «Обследование пациентов» размером 8*20, приведенную ниже.
| Ф.И.О. пациента | Пол | Возраст | Рост (см) | Фактический вес | Расчетный вес | Разность между фактическим и расчетным весом | Патология в весе |
| Ашотов С.М. | Муж. | 30 | 175 | 70 | |||
| Бирюкова Е.А. | Жен. | 25 | 173 | 54 | |||
| … | … | …. | … | … |
Заполнить последние столбцы таблицы, учитывая, что нормальная масса тела (в кг) рассчитывается по следующей формуле: 50+0,75*(рост-150)+(возраст-20)/4, а диагноз ожирение ставят, когда масса тела увеличивается больше, чем на 5 кг (по сравнению с нормой). Выделить красным цветом фамилии пациентов, страдающих ожирением. Сохранить файл под именем«Patient.sta» в папке с Вашим именем на Рабочем столе.
Указание. В столбец Var6 ввести формулу «=50+0,75*(v4-150)+(v3-20)/4», в столбец Var7 - формулу «=v5-v6», в столбец Var8 - формулу «=iif(v7>=5;1;0)», где «1» будет означать ожирение, а «0» - нормальный вес.
|
|
|
4. В программе «Statistica 10» создать таблицу «Смертность от ишемической болезни сердца (ИБС) в некоторых странах, 2013 г.», размером 1*11, приведенную ниже. На основании данных построить круговую и столбчатую диаграммы.
Указание: Переименовать строки в названия стран.
| Страна | Смертность от ИБС на 100 тыс. населения |
| Молдова | 496,16 |
| Украина | 491,91 |
| Кыргызстан | 444,59 |
| Россия | 359,33 |
| Литва | 313,91 |
| Латвия | 248,88 |
| Эстония | 199,15 |
| Румыния | 187,19 |
| Казахстан | 181,32 |
| Чехия | 161,82 |
| Болгария | 114,26 |
v Краткая теория
Программа «Statistica» представляет собой интегрированную систему статистического анализа и обработки данных.
Статистический анализ данных в программе «Statistica» состоит из следующих основных этапов:
1. Ввод данных в электронную таблицу и их предварительное преобразование (построение необходимых выборок, упорядочивание и т.д.).
2. Представление данных с помощью одного из типов графиков.
3. Применение конкретной процедуры статистической обработки.
4. Вывод результатов анализа в виде графиков и электронных таблиц с численной и текстовой информацией.
|
|
|
5. Подготовка и печать отчета.
Программа «Statistica» работает с четырьмя различными типами документов:
· электронная таблица «Spreadsheet», предназначена для ввода исходных данных и их преобразования. Электронные таблицы хранятся в файлах с расширением *.sta.
· таблица «Scrollsheet» предназначена для вывода численных и текстовых результатов анализа.
· график - документ в специальном графическом формате для графического представления численной информации. Графики хранятся в файлах с расширением *.stg.
· отчет - документ для вывода текстовой, численной и графической информации. Отчеты хранятся в файлах с расширением *.str.
Файлы данных могут объединяться в рабочую книгу «Workbook», которая имеет расширение *.stw.
Работа с программой «Statistica» начинается с ее запуска.
Запуск программы:
1) Пуск → Программы → Statistica;
2) Двойной щелчок левой кнопкой мыши по ярлыку программы на рабочем столе.
После запуска программы появится главное рабочее окно (рисунок 1.1).
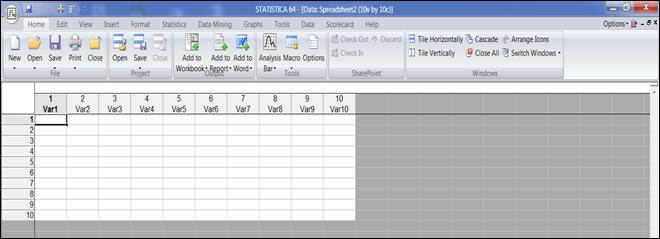
Рисунок 1.1. Рабочее окно программы «Statistica»
Рабочее окно программы «Statistica» состоит из следующих элементов:
· название документа;
|
|
|
· строка меню;
· панель инструментов;
· рабочая область.
В рабочую область выводятся все документы, которые получаются в ходе анализа.
Создание новой таблицы исходных данных: Home → File → New → Spreadsheet.
Электронная таблица состоит из столбцов «Variables» (Переменные) (Var1, Var2, …) и строк «Cases» (Случаи) (1, 2, …).
Размер таблицы по умолчанию принят 10*10 (10 столбцов и 10 строк).
Размер таблицы можно регулировать с помощью команд контекстного меню: «Delete Variables» (Удалить переменные), «Add Variables» (Добавить переменные), «Delete Cases» (Удалить случаи), «Add Cases» (Добавить случаи) или нажатием соответствующих кнопок на панели инструментов.
Можно задавать заголовок таблицы, имена переменных и случаев. В качестве имен случаев можно использовать числа, текст, даты.
Свойства переменной (имя, формат, код пропущенных значений, метка, формула для вычисления или связь) называют спецификацией переменной и устанавливают с помощью двойного щелчка левой кнопкой мыши по имени переменной (например, «Var1»).
Строки (Случаи) и столбцы (Переменные) можно копировать (команда «Copy»), вырезать (команда «Cut»), очищать (команда «Clear»), перемещать (команда «Move»)и т.д.
Строки, столбцы, отдельные ячейки можно выделять различными цветами. Для этого выделить необходимый диапазон и нажать кнопку «Background Color» (Заливка) в меню «Format».
Пример 1.1. В программе «Statistica 10» создать таблицу «Артериальное давление» размером 6*15. В таблице представить результаты воздействия лекарства «Каптоприл» на артериальное давление (АД). Сохранить файл под именем «Arterial_pressure.sta» в папке с Вашим именем на Рабочем столе. Исходные данные содержатся в следующей таблице.
| Верхняя граница АД до приема препарата | Верхняя граница АД после приема препарата | Разность | Нижняя граница АД до приема препарата | Нижняя граница АД после приема препарата | Разность |
| 210 | 201 | 130 | 125 | ||
| 169 | 165 | 122 | 121 | ||
| 187 | 166 | 124 | 121 | ||
| 160 | 157 | 104 | 105 | ||
| 167 | 147 | 112 | 101 | ||
| 176 | 145 | 101 | 85 | ||
| 185 | 168 | 121 | 98 | ||
| 206 | 180 | 124 | 105 | ||
| 173 | 147 | 115 | 103 | ||
| 146 | 136 | 102 | 98 | ||
| 174 | 151 | 98 | 90 | ||
| 201 | 168 | 119 | 98 | ||
| 198 | 179 | 106 | 110 | ||
| 148 | 129 | 107 | 103 | ||
| 154 | 131 | 100 | 82 |
1. Создание электронной таблицы.
Открыть программу «Statistica 10». На экране автоматически появится электронная таблица размером 10*10. Если таблица не появилась, то выполнить команды: Home →File →New→Spreadsheet.
2. Настройка размеров таблицы.
Для данных требуется 6 столбцов и 15 строк. Удалить лишние 4 столбца и добавить 5 строк.
Чтобы удалить лишние столбцы нужно установить курсор на поле с заголовками переменных (Var1, Var2, … , Var10), щелчком правой кнопки мыши вызвать контекстное меню. Выбрать команду «Delete Variables» (Удалить переменные) (рисунок 1.2), указать диапазон удаляемых переменных (рисунок 1.3) и нажать кнопку «ОK».
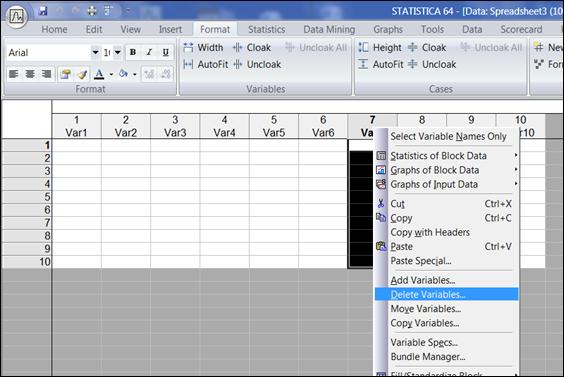
Рисунок 1.2. Контекстное меню
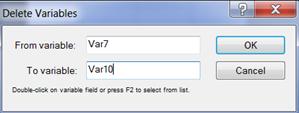
Рисунок 1.3. Удаление переменных (столбцов)
Чтобы добавить строки, нужно установить курсор на поле с заголовками случаев (1, 2, …, 10), щелчком правой кнопки мыши вызвать контекстное меню. Выбрать команду «Add Cases» (Добавить случаи), указать диапазон добавляемых случаев (рисунок 1.4) и нажать кнопку «ОK».
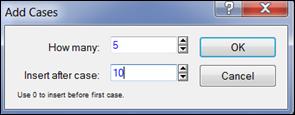
Рисунок 1.4. Добавление случаев (строк)
3. Оформление заголовка таблицы.
Заголовок таблицы «Артериальное давление» ввести в белое поле под строкой: «Data: Spreadsheet1 (6v by 15c)» (рисунок 1.5).
 Рисунок 1.5. Оформление заголовка таблицы
Рисунок 1.5. Оформление заголовка таблицы
4. Задание имен переменных.
Дважды щелкнуть левой кнопкой мыши по имени переменной «Var1». В поле «Name» (Имя) написать «Верхняя граница АД до приема препарата». Нажать кнопку «>>», перейти в следующий столбец. Переменной «Var2» присвоить имя «Верхняя граница АД после приема препарата». Так же задать имена переменным «Var4» и «Var5». Если имена видны частично, то растянуть столбцы.
5. Ввод данных в электронную таблицу.
Ввести данные в электронную таблицу с клавиатуры. При этом столбцы «Var3» и «Var6» останутся незаполненными.
6. Вычисление значений переменной по формуле.
Дважды щелкнуть левой кнопкой мыши по имени переменной «Var3». В поле «Long name» (Длинное имя) записать формулу для вычисления «=v2-v1» (рисунок 1.6) и нажать кнопку «OK».
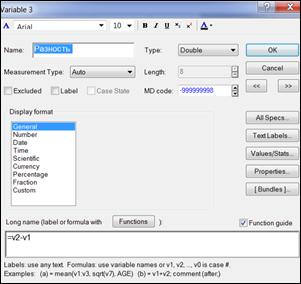
Рисунок 1.6. Ввод формулы
Аналогичным образом вычислить и вывести значения «Var6». Переменным «Var3» и «Var6» задать имя «Разность» (рисунок 1.7).
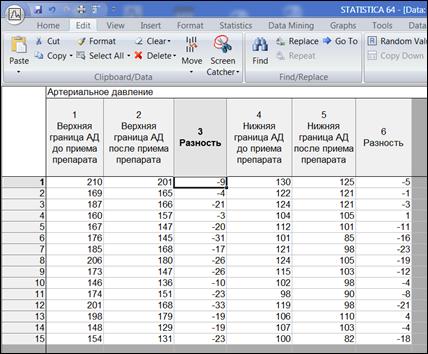
Рисунок 1.7. Результаты вычислений по формулам
7. Сохранение файла данных.
Выполнить команды: Home→File→Save→Save As изадать имя файла «Arterial_ pressure.sta».
Графики и диаграммы – один из самых наглядных способов представления результатов исследования.
В программе «Statistica» представлено большое количество разнообразных графиков. График можно построить с помощью меню «Graphs» (Графики) или вызвав контекстное меню, щелкнув правой кнопкой мыши на ячейке данных.
Кроме того, графики можно строить в любом статистическом модуле на любом шаге анализа.
После выбора нужного типа графика необходимо задать переменные (Variables), подлежащие анализу, при необходимости изменить настройки графика.
Рассмотрим построение некоторых простейших графиков.
Пример 1.2. В программе «Statistica 10» создать таблицу «Смертность от рака среди населения стран СНГ в 2013 г.» размером 1*7. Переименовать строки в названия стран СНГ (рисунок 1.8).
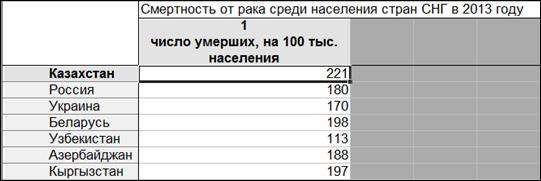
Рисунок 1.8. Таблица исходных данных для примера 2.
Построить круговую диаграмму (Pie Charts).
Graphs→2D→ Pie Charts (рисунок 1.9).
Рисунок 1.9. Выбор типа диаграммы
Во вкладке «Advanced» (Дополнительный) выбрать «Pie Charts – Values» (Круговая диаграмма значений) и задать переменную «Variables» (рисунок 1.10), нажать кнопку «OK».
Рисунок 1.10. Выбор переменной для круговой диаграммы.
Во вкладке «Advanced» нажать кнопку «Spreadsheet», выбрать «Case names» (Имена случаев). В окне «Pie legend» (Легенда диаграммы) выбрать «Text and Percent» (Текст и проценты) (рисунок 1.11), нажать кнопку «OK».
Рисунок 1.11. Выбор параметров круговой диаграммы
Получить круговую диаграмму (рисунок 1.12).
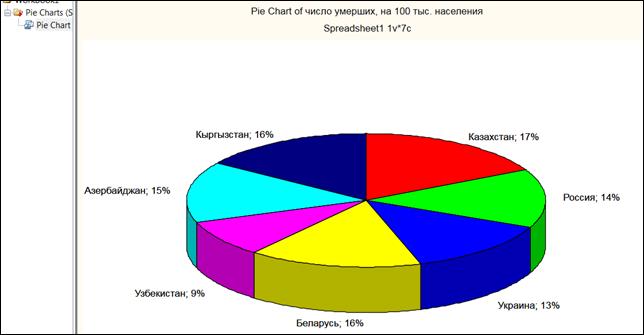
Рисунок 1.12. Круговая диаграмма
Щелкнув два раза левой кнопкой мыши на графике можно менять его свойства (задавать фон, поворачивать, менять цвета надписей и др.) (рисунок 1.13).
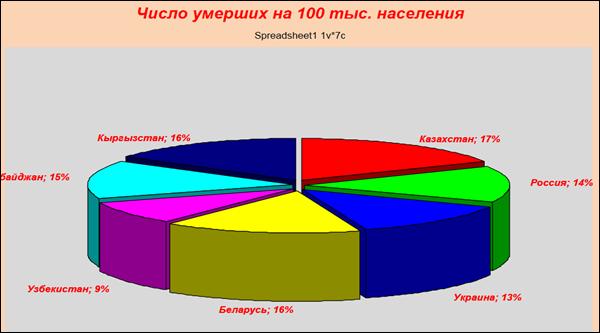
Рисунок 1.13. Форматирование графика
Построить столбчатую диаграмму (Bar/Column Plots).
Graphs→2D→ Bar/Column Plots (рисунок 1.14).
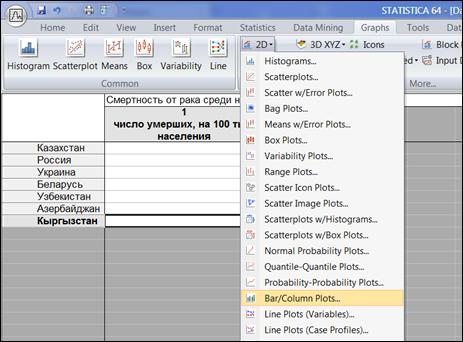
Рисунок 1.14. Выбор типа диаграммы
Во вкладке «Advanced» выбрать «Graph type» (Тип графика) – «Regular» (Простой), «Orientation» (Ориентацию) – «Vertical» (Вертикальную) и задать переменную «Variables» (рисунок 1.15), нажать кнопку «OK».
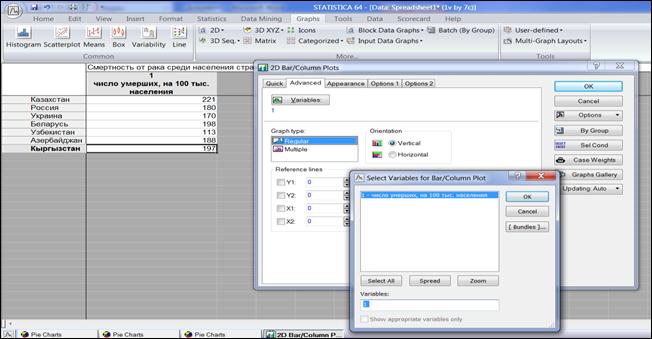
Рисунок 1.15. Выбор переменной для столбчатой диаграммы
Перейти во вкладку «Options1», нажать кнопку «Spreadsheet», выбрать «Case names» (рисунок 1.16), нажать кнопку «OK».
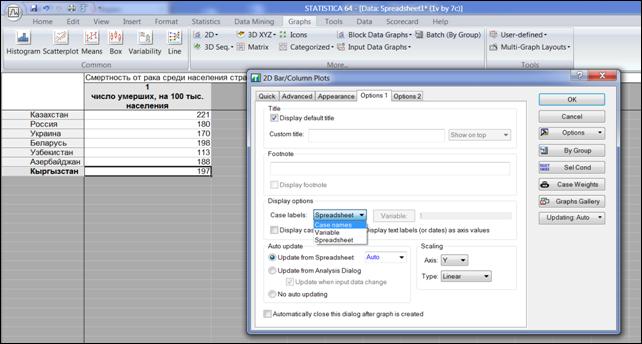
Рисунок 1.16. Выбор параметров столбчатой диаграммы
Получить столбчатую диаграмму (рисунок 1.17).
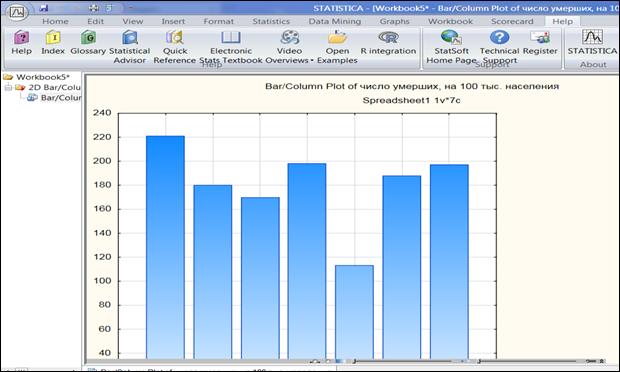
Рисунок 1.17. Столбчатая диаграмма
Чтобы была видна «легенда» щелкнем левой кнопкой мыши в левой области рабочей книги (рисунок 1.18).
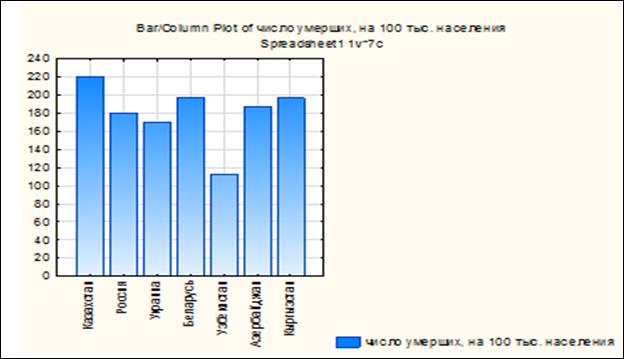
Рисунок 1.18. Столбчатая диаграмма с легендой
Пример 1.3. В программе «Statistica 10» создать таблицу «Изучение взаимосвязи между показателями» размером 2*12. Переименовать строки в названия месяцев (рисунок 1.19).
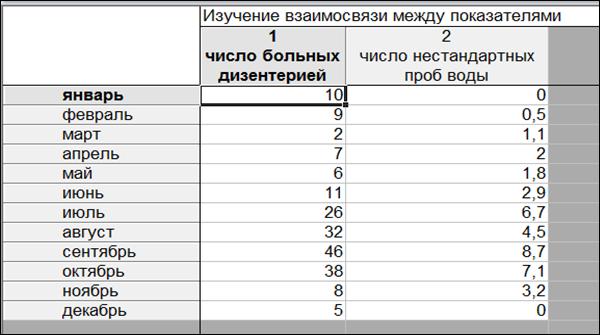
Рисунок 1.19. Таблица исходных данных для примера 1.3
Построить диаграмму рассеяния (Scatterplot).
Graphs→2D→ Scatterplot (рисунок 1.20).
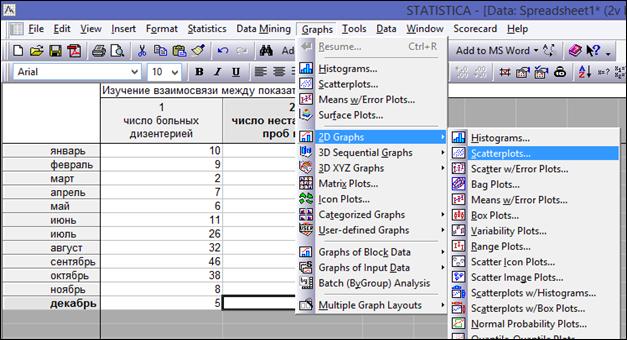
Рисунок 1.20. Выбор типа диаграммы
Во вкладке «Advanced» (Дополнительный) задать переменные «Variables» (рисунок 1.21) и нажать кнопку «OK».
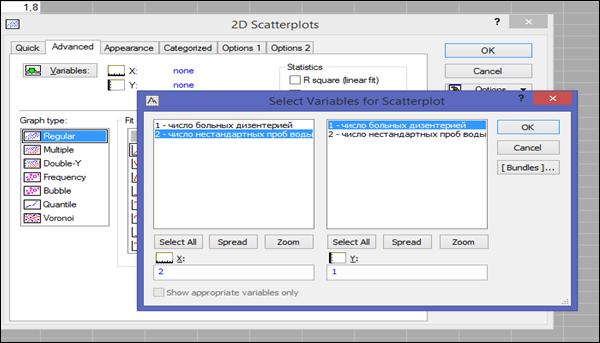
Рисунок 1.21. Выбор переменных для диаграммы рассеяния.
Во вкладке «Advanced» выбрать опции «R square (linear fit)» (R-квадрат – коэффициент детерминации) и «Regression (fit) equation» (Уравнение регрессии) (рисунок 1.22), нажать кнопку «OK».
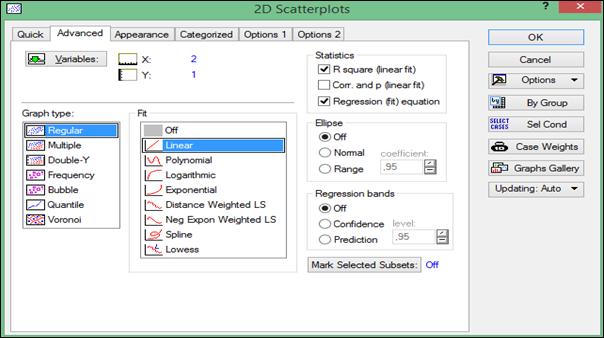
Рисунок 1.22. Выбор параметров для диаграммы рассеяния
Получить диаграмму рассеяния (рисунок 1.23).
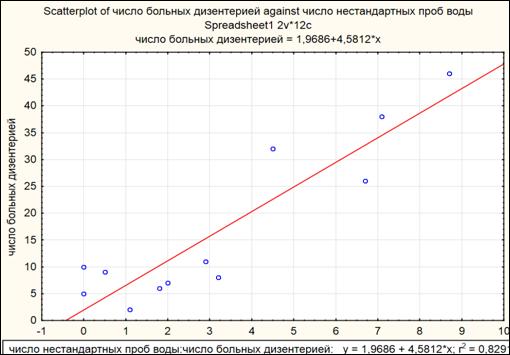
Рисунок 1.23. Диаграмма рассеяния
В нижней части графика показано уравнение регрессии и коэффициент детерминации.
Пример 1.4. В программе Statistica 10 создать таблицу «Рост и вес 30-летних мужчин и женщин» размером 2*27 (рисунок 1.24).
Построить диаграмму «Ящик с усами» (Box Whiskers).
Graphs→2D→ Box plots (рисунок 1.25).
Рисунок 1.24. Таблица исходных данных для примера 1.4
Рисунок 1.25. Выбор типа диаграммы
Во вкладке «Quick» (Быстрый) задать переменные «Variables» (рисунок 1.26) и нажать кнопку «OK».
Рисунок 1.26. Выбор переменных для диаграммы «Ящик с усами»
Получить диаграмму «Ящик с усами» (рисунок 1.27).
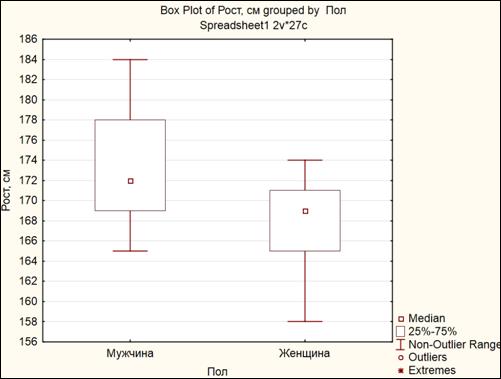
Рисунок 1.27. Диаграмма «Ящик с усами»
6. Литература:
1. Боровиков В.П. Популярное введение в программу STATISTICA. - М.: Компьютер Пресс, 1998. - 240 с.
2. Боровиков В.П. STATISTICA. Искусство анализа данных на компьютере: для профессионалов / В. Боровиков. - СПб.: Питер, 2004. - 688 с.
3. Реброва О.Ю. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA. - М.: Медиасфера, 2002. - 312с.
4. Халафян А.А. Statistica 6. Статистический анализ данных. 3-е изд. Учебник - М.: ООО «Бином-Пресс», 2007. - 512 с.
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №2
1. Тема: Основные виды случайных величин в биомедицине. Дискретные и непрерывные случайные величины. Законы распределения случайных величин. Анализ случайных величин с помощью программы «Statistica».
2. Цель: Формирование понятия о случайных величинах: виды, числовые характеристики и законы распределения.
3. Задачи обучения:Научитьнаходить функции распределения случайных величин, определять их числовые характеристики, задавать закон распределения, анализировать случайные величины с помощьюпрограммы «Statistica».
4. Основные вопросы темы:
1. Что такое случайная величина? Какие виды случайных величин Вы знаете?
2. Как задается закон распределения дискретной случайной величины?
3. Как задается закон распределения непрерывной случайной величины?
4. Какие числовые характеристики случайных величин Вы знаете?
5. Как можно построить закон распределения дискретной случайной величины в программе «Statistica»?
6. Для чего используется процедура «Probability calculator» в программе «Statistica»?
5. Методы обучения и преподавания: письменное решение задач, статистическая обработка данных с помощью программы «Statistica 10».
v Задания:
1. Ознакомиться с краткой теорией практического занятия №2.
2. Ответить на основные вопросы темы.
3. Выполнить примеры 2.1, 2,2.
4. Закон распределения дискретной случайной величины «Х» задан таблицей:
| Х | 1 | 2 | 3 | 4 | 5 |
| Р | 0,2 | 0,3 | 0,35 | 0,1 | 0,05 |
Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение. Найти функцию распределения и построить ее график.
5. Число вызовов скорой помощи за один час – это дискретная случайная величина «Х», которая задана законом распределения:
| Х | 0 | 1 | 2 | 3 | 4 |
| Р | 0,13 | 0,35 | 0,35 | 0,15 | 0,02 |
Вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение. Найти функцию распределения и построить ее график.
6. Медсестра обслуживает шестерых больных. Вероятность того, что в течение часа больному потребуется помощь медсестры, равна 0,4. Найти вероятность того, что не более чем 4 больным потребуется помощь медсестры в течение часа.
Указание: для решения использовать программу «Statistica 10».
7. Вероятность рождения мальчика и девочки одинаковая, т.е. 0,5. Для семьи, имеющей пять детей, записать закон распределения случайной величины «Х», которая выражает число мальчиков в этой семье.
Указание: для решения использовать программу «Statistica 10».
8. Вероятность появления микроорганизмов в определенных условиях равна 0,7. Записать биномиальное распределение вероятностей появления микроорганизмов в шести случайно взятых пробах.
Указание: для решения использовать программу «Statistica 10».
9. Вероятность того, что среди стандартных ампул имеются ампулы с дефектом, равна 0,25. Записать биномиальное распределение вероятностей бездефектных случайно взятых 6 ампул.
Указание: для решения использовать программу «Statistica 10».
10.Вероятность всхожести семян лекарственного растения равна 0,9. Записать биномиальное распределение вероятностей появления всхожести семян из пяти случайно взятых семян.
Указание: для решения использовать программу «Statistica 10».
11.При изготовлении ампул вероятность появления стандартной ампулы с лекарственным веществом равна 0,97. Найти вероятность того, что из 15 случайно взятых ампул 14 будут стандартными.
Указание: для решения использовать программу «Statistica 10».
12.Случайная величина «Х» подчиняется нормальному закону распределения с математическим ожиданием µ=30 и дисперсией σ2=100. Найти вероятность того, что значение случайной величины находится между 10 и 50.
Указание: проверить решение задачи с помощью процедуры «Probability calculator» программы «Statistica 10».
13.Для человека рН крови является случайной величиной, имеющей нормальное распределение с математическим ожиданием µ=7,4 и средним квадратическим отклонением σ=0,2. Найти вероятность того, что уровень рНнаходится между 7,35 и 7,45.
Указание: проверить решение задачи с помощью процедуры «Probability calculator» программы «Statistica 10».
v Краткая теория
Величина, принимающая любые числовые значения в зависимости от различных случайных обстоятельств, называется случайной величиной.
Случайные величины делятся на дискретные (прерывные) и непрерывные.
Случайная величина называется дискретной, если она принимает отдельные друг от друга числовые значения.
Случайная величина называется непрерывной, если она может принимать все значения из некоторого конечного или бесконечного интервала.
Соответствие между возможными значениями дискретной случайной величины «хi» и их вероятностями «pi» называется законом распределения этой величины и задается в виде таблицы (таблица 2.1).
Таблица 2.1.
| Х | х 1 | х2 | … | xi | … | xn |
| Р | p1 | p2 | … | pi | … | pn |
Функцией распределения называется функция «F(x)», равная вероятности 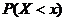 того, что случайная величина «Х» примет значение меньше, чем ее возможное значение «x»:
того, что случайная величина «Х» примет значение меньше, чем ее возможное значение «x»:
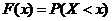 . (2.1)
. (2.1)
Закон распределения полностью характеризует дискретную случайную величину. Однако во многих случаях он неизвестен, поэтому используют числовые характеристики дискретных случайных величин:
· Математическое ожидание (µ или М(Х)) – приближенно равно среднему арифметическому наблюдаемых значений случайной величины:
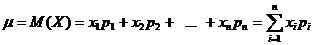 . (2.2)
. (2.2)
· Дисперсия (σ2 или D(Х)) - степень разброса случайной величины от ее среднего значения:
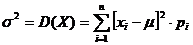 . (2.3)
. (2.3)
Упрощенная формула дисперсии:
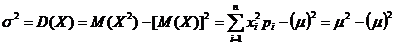 . (2.4)
. (2.4)
· Среднее квадратическое отклонение (σ) случайной величины:
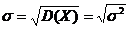 . (2.5)
. (2.5)
Рассмотрим непрерывную случайную величину «Х», возможные значения которой заполняют интервал [а, b].
Закон распределения вероятностей такой величины должен позволить найти вероятность попадания ее значения в любой заданный интервал (х1, х2), лежащий внутри [а,b].
Эту вероятность обозначают Р(х1<Х<х2) и вычисляют по формуле
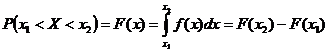 , (2.6)
, (2.6)
где F(x) - функция распределения, f(x) – плотность распределения.
Функция «f(х)», называемая плотностью распределения вероятностей, полностью характеризует непрерывную случайную величину «Х».
Основные числовые характеристики непрерывных случайных величин:
· Математическое ожидание (µ)
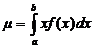 . (2.7)
. (2.7)
· Дисперсия ( 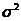 )
)
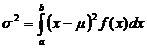 . (2.8)
. (2.8)
Упрощенная формула дисперсии:
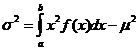 . (2.9)
. (2.9)
В программе «Statistica» большое внимание уделено анализу случайных величин, их числовых характеристик и законов распределения.
Рассмотрим решение задачи с дискретным распределением
Пример 2.1. В среднем 30% студентов сдают экзамен по биостатистике на «отлично». Найти вероятность того, что в группе из 15 студентов, не более пяти студентов получат «отлично».
1. Создать пустую электронную таблицу размера 16*2.
2. В первом столбце «Var1» ввести возможное число студентов, сдавших на «отлично» (0, 1, 2, …, 15) (количество испытаний).
3. Дважды щелкнуть по имени переменной «Var2». В нижней части окна в поле «Longname» записать «=Binom(v1;0,3;15)», где v1- количество испытаний, 0,3 - вероятность сдать экзамен на отлично, 15 - количество испытаний (рисунок 2.1). Нажать кнопку «OK».
4. Программа вычислит вероятности и занесет их в столбец «Var2».
5. Выделить первые 6 элементов столбца «Var2», вызвать контекстное меню, выбрать Statistics of Block Data (Статистика блока данных)→Block Columns (Блок столбцов)→Sums (Суммы) (рисунок 2.2). Появится число 0,72162144, которое означает вероятность того, что экзамен на «отлично» сдадут не более чем 5 студентов.
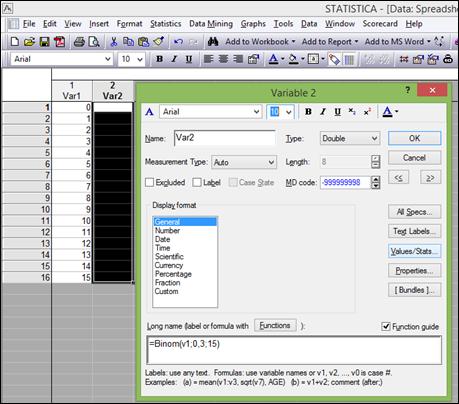
Рисунок 2.1. Ввод формулы
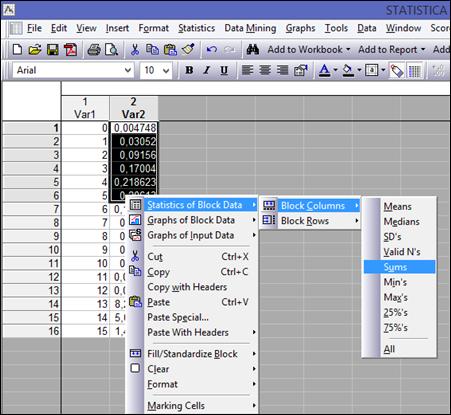
Рисунок 2.2. Вычисление суммы диапазона ячеек
В программе «Statistica» есть специальная процедура «Probability calculator» (Вероятностный калькулятор), с ее помощью можно выполнять следующие действия:
· строить графики функции распределения и плотности распределения;
· для непрерывных случайных величин определять вероятность попадания значений в заданный интервал;
· для дискретных случайных величин вычислять вероятности и строить ряды распределения.
Рассмотрим принципы работы процедуры «Probability calculator».
Запуск: Statistics→Basic statistics and Tables → Probability calculator (рисунок 2.3), нажать кнопку «OK».
Рисунок 2.3. Выбор процедуры «Probability calculator»
Откроется рабочее окно команды «Probability Distribution Calculator» (Калькулятор вероятностных распределений)(рисунок 2.4).
В левой части окна расположен список распределений. Когда пользователь выбирает вид распределения, справа появляются поля, где задаются параметры распределения: «mean» (среднее), «st. dev.» (среднее квадратическое отклонение), а также графики плотности и функции распределения. В поле «р» задается значение вероятности. После нажатия кнопки «Compute» (Подсчет) в поле «Х» появится значение квантиля, соответствующее заданной вероятности. Так же можно по заданному значению «Х» вычислить вероятность «р».
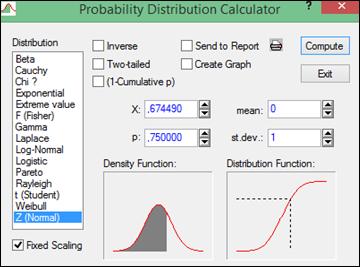
Рисунок 2.4. Рабочее окно команды «Probability Distribution Calculator»
Пример 2.2. Рост студентов подчинен нормальному распределению: µ=175,6 см, σ=7,63 см. Случайно выбирается студент. Какова вероятность того, что рост этого студента не больше 185 и не меньше 175 см?
1. Запустить Probability calculator : Statistics→Basic statistics and Tables→ Probability calculator→OK.
2. В списке распределений выбрать нормальное «Z (Normal)».
3. Заполнить поля: «mean» - 175,6, «st. dev.» - 7,63, «Х» - 185.Нажать кнопку «Compute». В поле «р» появится значение 0,891022 (рисунок 2.5). Запомним его как «р1».
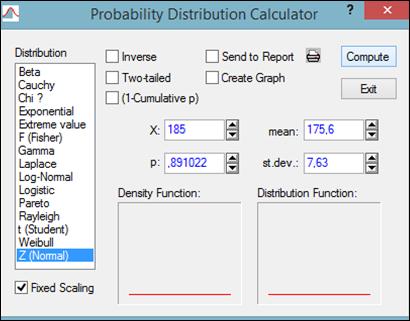
Рисунок 2.5. Результаты вычислений команды «Probability Distribution Calculator»
4. В поле «Х» задать 175.Нажать кнопку «Compute». В поле «р» появится значение 0,468661 запомним его как «р2».
5. Вычислить: р1 - р2=0,422361. Это вероятность того, что случайный студент имеет рост не ниже 175 и не выше 185 см.
6. Литература:
1. Боровиков В.П. Популярное введение в программу STATISTICA. - М.: Компьютер Пресс, 1998. - 240 с.
2. Боровиков В.П. STATISTICA. Искусство анализа данных на компьютере: для профессионалов / В. Боровиков. - СПб.: Питер, 2004. - 688 с.
3. Лобоцкая Н.Л. Высшая математика. / Н.Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. - Мн.: Высшая школа, 1987. - 319 с.
4. Реброва О.Ю. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA.-М.: Медиасфера, 2002.- 312с.
5. Халафян А.А. Statistica 6. Статистический анализ данных. 3-е изд. Учебник - М.: ООО «Бином-Пресс», 2007. - 512 с.
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №3
1. Тема: Статистическая группировка и сводка данных. Оценка параметров генеральной совокупности с помощью выборочного метода. Доверительный интервал. Дискретный и интервальный статистические ряды распределения, их числовые характеристики. Графическое представление рядов распределения.
2. Цель: Знакомство с понятиями генеральной и выборочной совокупности, а также с процедурами оценки параметров генеральной совокупности, построения доверительных интервалов, вычисления числовых характеристик статистических рядов и их графического представления.
3. Задачи обучения: Сформировать навыки работы со статистическими совокупностями: производить группировку данных, вычислять числовые характеристики, оценивать параметры, определять доверительные интервалы, строить полигоны и гистограммы.
4. Основные вопросы темы:
1. В чем заключается суть выборочного исследования?
2. Какое применение выборочное исследование находит в медицине, здравоохранении и фармации?
3. Что такое генеральная и выборочная совокупность?
4. Что такое вариационный ряд?
5. Что такое полигон и гистограмма?
6. Какие числовые характеристики выборки Вы знаете?
7. Как строятся точечные оценки для параметров распределения?
8. Как строятся интервальные оценки для параметров распределения?
5. Методы обучения и преподавания: письменное решение задач.
v Задания:
1. Ознакомиться с краткой теорией практического занятия №3.
2. Ответить на основные вопросы темы.
3. Имеются данные по клинической оценке тяжести серповидноклеточной анемии: 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 3; 4; 4; 5; 5; 5; 5; 6; 7; 9; 10; 11. Представить выборку в виде вариационного ряда, найти среднее значение, дисперсию, среднее квадратическое отклонение, коэффициент вариации, медиану, моду, 25-й и 75-й процентили, построить полигон и гистограмму. Можно ли считать, что выборка извлечена из совокупности с нормальным распределением?
4. Имеются данные по продолжительности (в секундах) физической нагрузки до развития приступа стенокардии у 12 человек с ишемической болезнью сердца: 289, 203, 359, 243, 232, 210, 251, 246, 224, 239, 220, 211. Найдите среднее, дисперсию, среднее квадратическое отклонение, коэффициент вариации, медиану, 25-й и 75-й процентили. Можно ли считать, что выборка извлечена из совокупности с нормальным распределением?
5. Имеются результаты оценки проницаемости сосудов сетчатки: 1,2; 1,4; 1,6; 1,7; 1,7; 1,8; 2,2; 2,3; 2,4; 6,4; 19,0; 23,6. Найдите среднее, дисперсию, среднее квадратическое отклонение, коэффициент вариации, медиану, 25-й и 75-й процентили. Можно ли считать, что выборка извлечена из совокупности с нормальным распределением?
6. В течение 25 дней фиксировалось количество обратившихся за экстренной врачебной помощью. В результате получена выборка: 1, 0, 4, 2, 3, 5, 2, 4, 0, 1, 8, 5, 2, 4, 3, 3, 2, 5, 1, 3, 2, 5, 1, 3, 2. Представьте выборку в виде вариационного ряда, найдите среднее, дисперсию, среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
7. Выборочная проверка показала, что из 100 ампул с лекарственным препаратом 87 удовлетворяют стандарту. Мы хотим быть уверены на 95%, что не ошибаемся в оценке процента нестандартных изделий. В каких пределах находится этот процент? Каков должен быть объем выборки, чтобы оценить процент брака с точностью до 0,01?
8. В результате анализа стационарной помощи больным острым панкреатитом в больнице «А» были получены следующие данные:
| Длительность стационарного лечения, койко-дней | Число пациентов, чел. |
| 14 | 2 |
| 15 | 6 |
| 16 | 12 |
| 18 | 10 |
| 21 | 5 |
| Всего | 35 |
Соответствует ли представленный вариационный ряд закону нормального распределения? Рассчитайте показатели вариационного ряда: среднюю арифметическую величину, моду, медиану, дисперсию, среднеквадратическое отклонение.
9. Для исследования, посвященного лечению артериальной гипертонии, была набрана группа больных гипертонической болезнью со следующими параметрами артериального давления:
| Систолическое артериальное давление, мм рт.ст. | Число пациентов, чел. |
| 160 | 4 |
| 165 | 6 |
| 170 | 20 |
| 175 | 12 |
| 180 | 5 |
| Всего | 47 |
Соответствует ли представленный вариационный ряд закону нормального распределения? Рассчитайте показатели вариационного ряда: среднюю арифметическую величину, моду, медиану, дисперсию, среднеквадратическое отклонение.
10. В результате исследования сердечно-сосудистой системы у спортсменов-лыжников, были получены следующие данные:
| Частота сердечных сокращений за 1 мин | Число пациентов, чел. |
| 52 | 3 |
| 54 | 5 |
| 56 | 16 |
| 58 | 10 |
| 60 | 6 |
| Всего | 40 |
Соответствует ли представленный вариационный ряд закону нормального распределения? Рассчитайте показатели вариационного ряда: среднюю арифметическую величину, моду, медиану, дисперсию, среднеквадратическое отклонение.
11. Кафедрой акушерства и гинекологии был проведен социологический опрос, посвященный вопросам качества оказания амбулаторной акушерско-гинекологической помощи, среди беременных женщин. Получено следующее распределение опрошенных женщин по возрасту.
| Возраст, лет | Число пациентов, чел. |
| 18 | 5 |
| 20 | 10 |
| 24 | 15 |
| 25 | 12 |
| 28 | 8 |
| Всего | 50 |
Соответствует ли представленный вариационный ряд закону нормального распределения? Рассчитайте показатели вариационного ряда: среднюю арифметическую величину, моду, медиану, дисперсию, среднеквадратическое отклонение.
12. В исследовании нового антибиотика, обладающего высокой эффективностью, участвовали пациенты отделения гнойной хирургии, склонные к ожирению. Получено следующее распределение пациентов по массе:
| Масса тела, кг | Число пациентов, чел. |
| 90 | 1 |
| 100 | 4 |
| 120 | 8 |
| 130 | 6 |
| 140 | 2 |
| Всего | 21 |
Соответствует ли представленный вариационный ряд закону нормального распределения? Рассчитайте показатели вариационного ряда: среднюю арифметическую величину, моду, медиану, дисперсию, среднеквадратическое отклонение.
v Краткая теория
Статистическая совокупность – совокупность однородных по какому-либо признаку объектов, ограниченных пространством и временем.
Выборочный метод – метод статистического обследования, при котором из статистической совокупности выбирают ограниченное число объектов и их подвергают изучению.
Генеральная статистическая совокупность - это совокупность, которая состоит из бесконечно большого числа элементов.
Выборочная совокупность (выборка) - это совокупность, которая состоит из части выбранных элементов наблюдения, способных охарактеризовать всю генеральную совокупность.
Объем совокупности- это общее число элементов наблюдения. Объем генеральной совокупности обозначается «N», объем выборочной совокупности – «n». Если n≤30, то выборка считается малой.
Элемент наблюдения - это каждый частный случай явления, которое изучается.
Статистическое распределение выборки (или вариационный ряд) представляет собой таблицу, состоящую из двух столбцов (таблица 3.1).
Таблица 3.1.
| Варианты (xi) | Частоты (νi) |
| ... | ... |
| ... | ... |
| ... | ... |
| Всего: | n=Σ νi |
В первом столбце записываются значения варьирующего признака, называемые вариантами и обозначаемые «xi», а во втором столбце записываются числа, называемые частотами и обозначаемые «νi», показывающие сколько раз встречается каждый вариант.
Если варианты вариационного ряда выражены в виде дискретных величин (целых чисел), то такой вариационный ряд называют дискретным.
Дискретный вариационный ряд можно представить графически в виде многоугольника, называемого полигоном (рисунок 3.1).
|
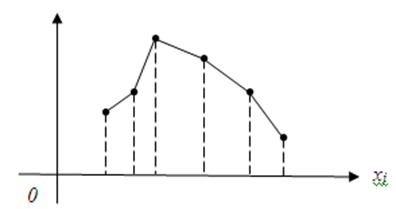
Рисунок 3.1. Полигон
Варианты признаков, которые могут принимать любые значения в определенном интервале, называют непрерывными.
Для непрерывных признаков строятся интервальные вариационные ряды.
Число интервалов «k» следует брать не очень большим, чтобы после группировки ряд не был очень объемным, и не очень малым, чтобы не потерять особенности распределения признака. Поэтому берут от 6 до 11 интервалов.
Согласно формуле Стерджеса рекомендуемое число интервалов:
k=1+3,322lgn. (3.1)
Например, так как lg100=2, для выборки объема 100 рекомендуемое число интервалов 8, а для выборки объема 50, число интервалов равно 5-6.
Формула для вычисления величины интервала «h»:
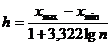 . (3.2)
. (3.2)
За начало первого интервала рекомендуется брать величину: хнач=xmin–0,5h.
Кроме того, необходимо следить, чтобы не было интервалов, в которые попало меньше 5 значений.
Интервальный вариационный ряд можно представить графически в виде ступенчатой фигуры, называемой гистограммой (рисунок 3.2).
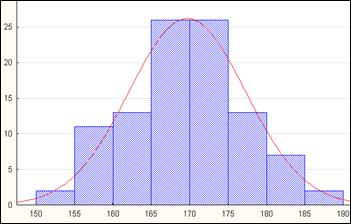
Рисунок 3.2. Гистограмма
Показатели центральной тенденции вариационного ряда.
Средние величины:
· средняя арифметическая простая
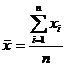 , (3.3)
, (3.3)
где n - общее число членов ряда;
· средняя арифметическая взвешенная
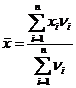 , (3.4)
, (3.4)
где νi – частоты.
Структурные величины:
· мода (Мо) – варианта с наибольшей частотой;
· медиана (Ме) – варианта, находящаяся в середине ряда;
· квантили - отдельные равные части, на которые разбивается вариационный ряд:
- квартили – величины, делящие вариационный ряд на четыре равные части;
- квинтили - величины, делящие вариационный ряд на пять равных частей;
- децили - величины, делящие вариационный ряд на десять равных частей;
- процентили - величины, делящие вариационный ряд на сто равных частей (рисунок 3.3).
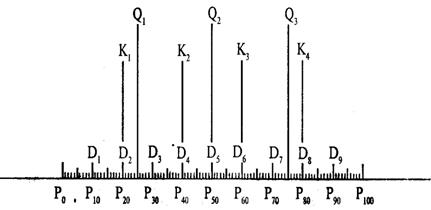
Рисунок 3.3. Структурные характеристики вариационного ряда
Нижний квартиль (Q1) или 25-й процентиль (P25) - это значение случайной величины, ниже которого находится 25% выборки. В ранжированном ряду номер нижнего квартиля определяется по формуле:
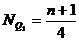 . (3.5)
. (3.5)
Верхний квартиль (Q3) или 75-й процентиль (P75) - это значение случайной величины, выше которого находится 25% выборки. В ранжированном ряду номер верхнего квартиля определяется по формуле:
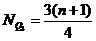 . (3.6)
. (3.6)
Если номер квартиля получится дробным, то его можно округлить до ближайшего целого.
К показателям разнообразия относятся:
· размах вариационного ряда
R=xmax – xmin, (3.7)
где xmax , xmin – наибольшее и наименьшее значения вариант соответственно;
· дисперсия - мера разброса случайной величины от ее среднего значения:
- если выборка задана вариационным рядом, то выборочная дисперсия определяется по формуле:
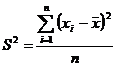 ; (3.8)
; (3.8)
- если выборка задана в виде таблицы, то выборочная дисперсия определяется по формуле:
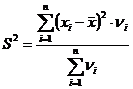 ; (3.9)
; (3.9)
· среднее квадратическое отклонение
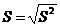 ; (3.10)
; (3.10)
· коэффициент вариации - мера разброса случайной величины, выраженная в процентах
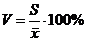 . (3.11)
. (3.11)
Если V≤33%, то выборка считается однородной.
Характеристики генеральной совокупности («Х» - генеральная средняя, «D» - генеральная дисперсия, «σ» - среднее квадратическое отклонение) называются параметрами.
Параметры обычно неизвестны, и их можно оценить на основе выборочных данных лишь приближенно. Эти приближенные значения называются оценками параметров генеральной совокупности.
Оценкой генеральной средней «Х» является выборочная средняя « 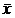 ».
».
Для того чтобы охарактеризовать рассеяние значений изучаемого признака выборки вокруг своего среднего значения « 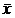 » вводят характеристику, называемую выборочной дисперсией «S2».
» вводят характеристику, называемую выборочной дисперсией «S2».
Оценкой генеральной дисперсии «D» является исправленная выборочная дисперсия «s2».
Исправленная выборочная дисперсия определяется по формуле
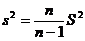 . (3.12)
. (3.12)
Оценкой «σ» - среднего квадратического отклонения генеральной совокупности является «s» - исправленное выборочное среднее квадратическое отклонение.
Исправленное выборочное среднее квадратическое отклонение определяется по формуле
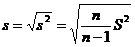 . (3.13)
. (3.13)
Средней ошибкой или средней квадратической ошибкой, или стандартной ошибкой среднего называется величина « 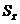 », определяемая по формуле:
», определяемая по формуле:
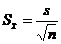 . (3.14)
. (3.14)
Эта величина характеризует стандартное отклонение выборочного среднего, рассчитанного по выборке объема «n» из генеральной совокупности.
Оценивание некоторого отдельного параметра дает точечную оценку.
Интервальной оценкой параметра генеральной совокупности называют интервал, который с заданной вероятностью «γ» накрывает истинное значение параметра.
Интервальную оценку называют доверительным интервалом, а связанную с ним вероятность «γ» – доверительной вероятностью или надежностью (в медицине и биологии γ=0,95).
Доверительный интервал для генеральной средней может быть получен из соотношения
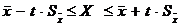 , (3.15)
, (3.15)
где 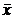 - выборочная средняя из «n» наблюдений,
- выборочная средняя из «n» наблюдений,  (γ;n-1)- табличная величина, зависящая от «γ» и «n»,
(γ;n-1)- табличная величина, зависящая от «γ» и «n», 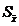 - стандартная ошибка среднего.
- стандартная ошибка среднего.
Объем выборки определяется по формуле
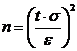 , (3.16)
, (3.16)
где n-объем выборки, σ – среднее квадратическое отклонение, 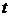 =1,96 – критическое значение стандартного нормального распределения при р=0,05 - табличная величина, ε =0,01 – заданная точность оценки, согласно ГОСТа.
=1,96 – критическое значение стандартного нормального распределения при р=0,05 - табличная величина, ε =0,01 – заданная точность оценки, согласно ГОСТа.
Если проводятся независимые испытания, в которых событие наступает с неизвестной вероятностью «р», то объем выборки определяется по формуле:
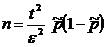 , (3.17)
, (3.17)
где 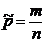 - оценка вероятности «р», m - число появлений события, n - общее число испытаний.
- оценка вероятности «р», m - число появлений события, n - общее число испытаний.
6. Литература:
1. Гланц С. Медико-биологическая статистика. Пер. с англ.-М.: Практика, 1998. - 459 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов / В.Е. Гмурман. - М.: Высшая школа, 2003. - 479 с.
3. Лобоцкая Н.Л. Высшая математика. / Н.Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. - Мн.: Высшая школа, 1987. - 319 с.
4. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах / Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
5. Основы высшей математики и математической статистики: Учебник / И.В. Павлушков и соавт. - М.: ГЭОТАР-МЕД, 2004. - 424 с.
6. Петри А., Сэбин К. Наглядная медицинская статистика /А. Петри, К. Сэбин; пер. с англ. - М.: ГЭОТАР-Медиа, 2009. - 168 с.
7. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие / ред. Кучеренко В.З. - М.: ГЭОТАР-Медиа, 2011. - 256 с.
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №4
1. Тема: Создание и анализ выборки с помощью программы «Statistica». Создание выборки чисел, подчиняющейся нормальному закону распределения, определение ее числовых характеристик с помощью программы «Statistica».
2. Цель: Знакомство с некоторыми возможностями программы «Statistica».
3. Задачи обучения: Сформировать навыки работы со статистическими совокупностями в программе «Statistica».
4. Основные вопросы темы:
1. Как создается выборка чисел, подчиняющаяся нормальному закону распределения, с помощью программы «Statistica»?
2. В каком модуле, с помощью какой процедуры производится вычисление числовых характеристик выборки, ее графическое изображение в программе «Statistica»?
5. Методы обучения и преподавания: статистическая обработка материалов с помощью компьютерной программы «Statistica 10».
v Задания:
1. Ознакомиться с краткой теорией практического занятия №4.
2. Ответить на основные вопросы темы.
3. Выполнить пример 4.1.
4. В программе «Statistica 10» создать выборку из 100 случайных чисел, имеющих нормальное распределение с параметрами: µ=18, σ=3,4, являющимися результатами измерения веса 5-летних девочек. Вычислить основные числовые характеристики выборки (медиану, среднее выборочное, дисперсию, среднеквадратическое отклонение и др.). Построить гистограмму, нормальный вероятностный график и график «ящик с усами». Объяснить результаты.
5. В программе «Statistica 10» создать выборку из 100 случайных чисел, имеющих нормальное распределение с параметрами: µ=100, σ=7,5, являющимися результатами измерения роста 4-летних мальчиков. Вычислить основные числовые характеристики выборки (медиану, среднее выборочное, дисперсию, среднеквадратическое отклонение и др.). Построить гистограмму, нормальный вероятностный график и график «ящик с усами». Объяснить результаты.
6. В программе «Statistica 10» создать выборку из 100 случайных чисел, имеющих нормальное распределение с параметрами: µ=120, σ=10,4, являющимися результатами измерения систолического артериального давления людей в возрасте от 20 до 40 лет. Вычислить основные числовые характеристики выборки (медиану, среднее выборочное, дисперсию, среднеквадратическое отклонение и др.). Построить гистограмму, нормальный вероятностный график и график «ящик с усами». Объяснить результаты.
7. В программе «Statistica 10» создать выборку из 100 случайных чисел, имеющих нормальное распределение с параметрами: µ=, σ=4,5, являющимися результатами измерения роста женщин в возрасте от 20 до 30 лет. Вычислить основные числовые характеристики выборки (медиану, среднее выборочное, дисперсию, среднеквадратическое отклонение и др.). Построить гистограмму, нормальный вероятностный график и график «ящик с усами». Объяснить результаты.
v Краткая теория
В программе «Statisticа» можно создавать выборки, подчиняющиеся равномерному, нормальному и пуассоновскому законам распределения.
Рассмотрим как создать выборку, подчиняющуюся нормальному закону распределения.
Дважды щелкнуть в таблице данных на имени переменной (например, «Var1»). В окне спецификации переменной нажать кнопку «Functions» (Функции). Выделить «All Functions» (Все функции) и выбрать функцию «RndNormal(X)». Эта функция имеет один параметр (Х), соответствующий среднему квадратическому отклонению случайной величины с математическим ожиданием, равным нулю. Запись «RndNormal(X)+μ» означает создание нормальной выборки чисел с математическим ожиданием «μ».
Формулы можно вводить вручную в соответствующее поле.
Анализ выборки осуществляется в модуле «Basic Statistics» (Основные статистики) с помощью процедуры «Descriptive statistics» (Описательные статистики).
Пример 4.1. В программе «Statistica 10» создать выборку из 100 случайных чисел, имеющих нормальное распределение с параметрами: µ=170, σ=7, являющимися результатами измерения роста студентов 1-го курса ЮКГФА.
Рассчитать: среднее значение, сумму, медиану, геометрическую среднюю, гармоническую среднюю, среднее квадратическое отклонение, дисперсию, стандартную ошибку среднего, доверительный интервал для среднего, асимметрию, эксцесс, наибольшее и наименьшее значение выборки, нижний и верхний квартили, размах.
Построить гистограмму и нормальный вероятностный график, а так же график «ящик с усами». Объяснить результаты.
1. Создание электронной таблицы.
Открыть программу «Statistica 10». На экране появится электронная таблица размером 10*10. Если таблица не появилась, то выполнить действия: Home →File →New→Spreadsheet.
2. Настройка размеров таблицы.
Для данных требуется 1 столбец и 100 строк. Удалить лишние 9 столбцов и добавить 90 строк.
3. Оформление заголовка таблицы.
Заголовок таблицы «Рост студентов 1-го курса ЮКГФА» ввести в белое поле под строкой «Data: Spreadsheet1 (1v by 100c)».
4. Задание имени переменной.
Дважды щелкнуть левой кнопкой мыши по имени переменной «Var1». Вызвать окно спецификации переменной. В поле «Name» (Имя) написать «Рост студентов, см», нажать кнопку «OK». Если имя видно частично, то растянуть столбец.
5. Создание выборки, подчиненной нормальному закону распределения.
Находясь в окне спецификации переменной «Var1» в поле «Long name» (Длинное имя) записать формулу «=RndNormal(7)+170» (рисунок 4.1), нажать кнопку «OK». Программа автоматически заполнит ячейки числами.
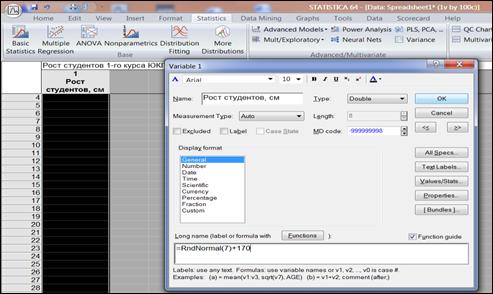
Рисунок 4.1. Создание выборки, подчиненной нормальному закону распределения
6. Изменение формата числовых данных.
В окне спецификации переменной «Var1» в поле «Display format» (Формат отображения) выбрать «Number» (Числовой), в поле «Decimal places» (Десятичные разряды) поставить «1», нажать кнопку «OK».
7. Вычисление числовых характеристик выборки.
Basic Statistics → Descriptive statistics (рисунок 4.2) → OK.
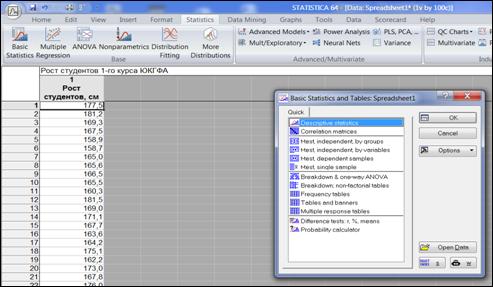
Рисунок 4.2. Выбор процедуры «Descriptive statistics»
Задать переменную «Variables» (рисунок 4.3).
Рисунок 4.3. Задание переменной
Выбрать вкладку «Advanced» (Дополнительно), отметить нужные числовые характеристики:
Valid N - объем выборки;
Mean - среднее;
Sum - сумма;
Median - медиана;
Geom. mean - геометрическая средняя;
Harm. mean - гармоническая средняя;
Standard Deviation - среднее квадратическое отклонение;
Variance - дисперсия;
Std. err. of mean - стандартная ошибка среднего;
Conf. limits for means - доверительный интервал для среднего;
Skewness - асимметрия;
Kurtosis - эксцесс;
Minimum & maximum - минимум и максимум;
Lower & upper quartiles - нижний и верхний квартили;
Range - размах (рисунок 4.4).
Нажать кнопку «Summary».
Рисунок 4.4. Выбор числовых характеристик
На экране появится итоговая таблица (рисунок 4.5).
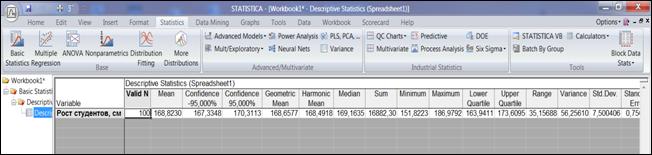
Рисунок 4.5. Итоговая таблица с числовыми характеристиками выборки
8. Построение гистограммы.
Вернуться в окно анализа «Descriptive statistics», выбрать вкладку «Normality» (Нормальность), нажать кнопку «Histograms» (Гистограммы) (рисунок 4.6).
Рисунок 4.6. Построение гистограммы
На экране появится гистограмма (рисунок 4.7). Красная линия на гистограмме - график плотности нормального распределения.
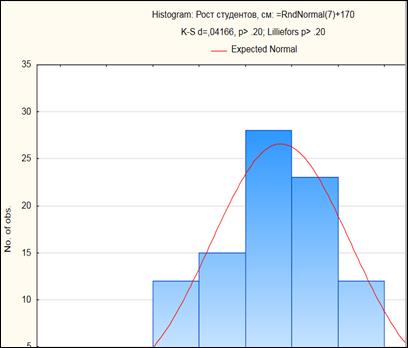
Рисунок 4.7. Гистограмма
9. Построение нормального вероятностного графика.
Вернуться в окно анализа «Descriptive statistics», выбрать вкладку «Prob. & Scatterplots» (Вероятностные графики и диаграммы рассеяния), нажать кнопку «Normal probability plot» (Нормальный вероятностный график) (рисунок 4.8).
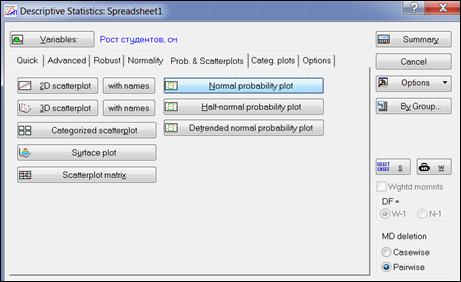
Рисунок 4.8. Построение нормального вероятностного графика
На экране появится нормальный вероятностный график (рисунок 4.9). Красная линия на гистограмме - плотность нормального распределения, синие точки - наблюдения выборки. Чем ближе синие точки располагаются к красной линии, тем распределение «нормальней».
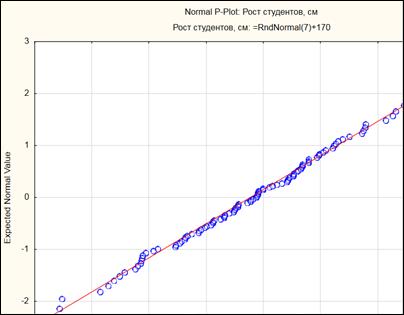
Рисунок 4.9. Нормальный вероятностный график
10. Построение графика «ящик с усами».
Вернуться в окно анализа «Descriptive statistics», выбрать вкладку «Quick» (Быстрый), нажать кнопку «Box & whisker plot for all variables» (График «ящик с усами» для всех переменных) (рисунок 4.10).
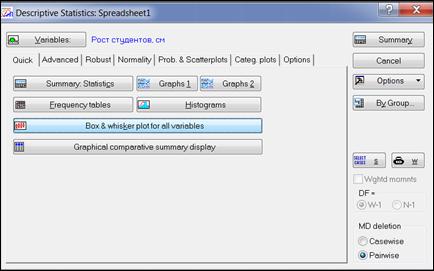
Рисунок 4.10. Построение графика «ящик с усами»
На экране появится график «ящик с усами» (рисунок 4.11). В «легенде», расположенной в нижней части графика, указаны: среднее и доверительные интервалы для среднего.
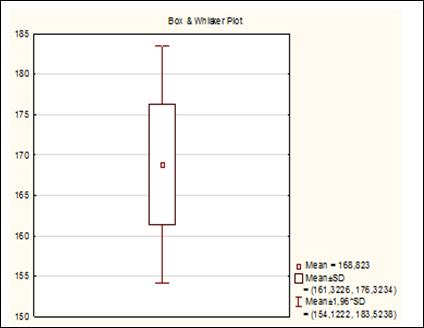
Рисунок 4.11. График «ящик с усами»
Если нужно чтобы в «легенде» графика содержалась информация о медиане, нижнем и верхнем квартилях, а также о размахе, то нужно выбрать вкладку «Options» и отметить «Median/Quartiles/Range» (рисунок 4.12), нажать кнопку «Sammary»,а затем опять построить график «ящик с усами» (рисунок 4.13).
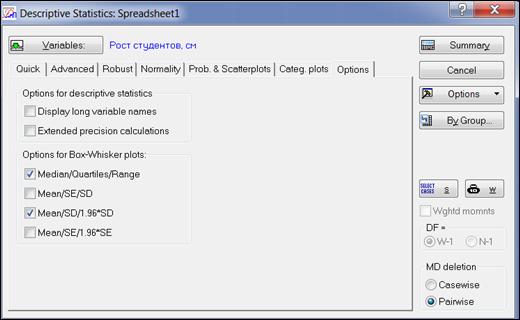
Рисунок 4.12. Выбор опций для графика «ящик с усами»
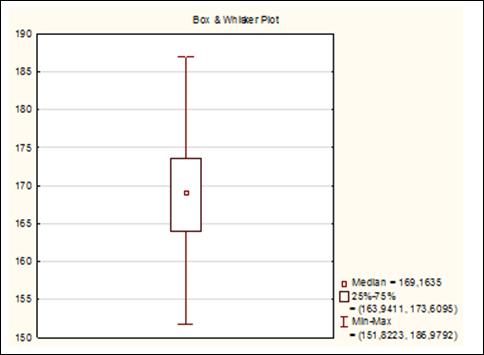
Рисунок 4.13. График «ящик с усами»
11. Сохранение данных.
На Рабочем столе создать папку «Student». В этой папке сохранить таблицу исходных данных под именем «Sample.sta»: Home→File→Save→Save As
В этой же папке сохранить рабочую книгу под именем «Analysis results.stw»: Home→File→Save→Save As
6. Литература:
1. Боровиков В.П. Популярное введение в программу STATISTICA. - М.: Компьютер Пресс, 1998. - 240 с.
2. Боровиков В.П. STATISTICA. Искусство анализа данных на компьютере: для профессионалов / В. Боровиков. - СПб.: Питер, 2004. - 688 с.
3. Реброва О.Ю. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA.- М.:Медиасфера, 2002.- 312с.
4. Халафян А.А. Statistica 6. Статистический анализ данных. 3-е изд. Учебник - М.: ООО «Бином-Пресс», 2007. - 512 с.
5. http://www.statsoft.ru/
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №5
1. Тема: Проверка статистических гипотез. Проверка нулевой гипотезы Н0 при конкурирующей гипотезе Н1. Критерий согласия χ2-Пирсона. Критерий согласия Колмогорова – Смирнова. Проверка гипотез о параметрах нормально распределенных совокупностей.
2. Цель: Знакомство с основами теории проверки статистических гипотез.
3. Задачи обучения: Сформировать навыки применения критериев согласия и проверки гипотез о параметрах нормально распределенных совокупностей.
4. Основные вопросы темы:
1. Что называется статистической гипотезой? Какие виды статистических гипотез Вы знаете?
2. Что называется ошибкой ошибкой первого и второго рода?
3. Что называется доверительной вероятностью и уровнем значимости?
4. Какова общая схема проверки статистичесикх гипотез?
5. Для чего используются критерии согласия?
6. Какова схема применения критерия согласия χ2-Пирсона?
7. Какова схема применения критерия согласия Колмогорова - Смирнова?
8. Какова схема проверки гипотезы о сравнении дисперсий двух нормальных генеральных совокупностей?
9. Какова схема проверки гипотезы о равенстве неизвестной дисперсии конкретному значению?
5. Методы обучения и преподавания: письменное решение задач.
v Задания:
1. Ознакомиться с краткой теорией практического занятия №5.
2. Ответить на основные вопросы темы.
3. Выборка объема n=200 из генеральной совокупности «Х» представлена в виде статистического ряда:
| хi | 0,3 | 0,5 | 0,7 | 0,9 | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 | 2,1 | 2,3 |
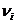
| 6 | 9 | 26 | 25 | 30 | 26 | 21 | 24 | 20 | 8 | 5 |
Проверить гипотезу о нормальном распределении генеральной совокупности «Х»с помощью критерия согласия χ2-Пирсона и критерия согласия Колмогорова - Смирнова при р=0,05.
4. Изучалось среднее артериальное давление (мм рт. ст.) в начальной стадии шока. Выборка объема n=50 представлена следующими числами: 112, 110, 107, 103, 108, 109, 111, 110, 103, 103, 109, 102, 113, 106, 108, 105, 108, 104, 99, 112, 112, 103, 101, 98, 100, 97, 98, 100, 98, 107, 108, 99, 98, 92, 98, 110, 106, 105, 102, 100, 101, 100, 95, 100, 105, 100, 102, 102, 99, 97.
Проверить гипотезу о нормальном распределении генеральной совокупности с помощью критерия согласия χ2-Пирсона и критерия согласия Колмогорова - Смирнова при р=0,05.
5. При лечении некоторого заболевания применяются две методики: «А» и «В». Эффективность методик характеризуется изменением численных значений определенного показателя. Отобраны две однородные группы больных. Первая группа с численностью n1=20, а вторая n2=15 человек. В первой группе (с методикой «А») значения рассмотренного показателя X1, X2,…, X20, во второй (с методикой «В») - Y1, Y2,…, Y15. Их генеральные совокупности распределены нормально. Для обеих групп средние значения показателя 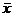 и
и 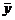 практически равны, а исправленные выборочные дисперсии
практически равны, а исправленные выборочные дисперсии 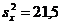 ,
, 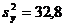 . Требуется сопоставить две методики лечения при уровне значимости
. Требуется сопоставить две методики лечения при уровне значимости 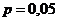 .
.
6. При производстве лекарственных препаратов руководствуются стандартом. Контролируется определенный показатель, допустимая характеристика рассеяния которого определена числом 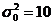 . Из произведенной партии продукции извлекается контрольная выборка объемом n=15 единиц продукции. Выборочная дисперсия контролируемого показателя
. Из произведенной партии продукции извлекается контрольная выборка объемом n=15 единиц продукции. Выборочная дисперсия контролируемого показателя 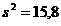 . Требуется по выборке проверить значимость различия дисперсий: наблюдаемой «
. Требуется по выборке проверить значимость различия дисперсий: наблюдаемой « 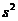 » и контрольной «
» и контрольной « 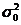 ». Также известно, что уровень значимости
». Также известно, что уровень значимости 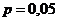 и генеральная совокупность распределена по нормальному закону.
и генеральная совокупность распределена по нормальному закону.
v Краткая теория
Гипотеза – это некоторое предположение о параметрах известных распределений (параметрическая) или о виде неизвестного закона распределения (непараметрическая) случайных величин, выдвигаемое в качестве предварительного, условного объяснения.
Для решения любой подобной задачи выдвигаются две статистические гипотезы:
- нулевая гипотеза Н0 - гипотеза об отсутствии различий между группами, либо об определенных значениях параметров, либо о соответствии распределения нормальному закону;
- альтернативная гипотеза Н1 - гипотеза о существовании различий между группами, либо об отличающихся от заданных значениях параметров, либо о несоответствии распределения нормальному закону.
Статистика – это функция от выборочных наблюдений, на основе которой принимается или отвергается нулевая гипотеза.
Статистическими критериями называются правила, согласно которым выясняется, соответствует или нет интересующая нас гипотеза опытным данным.
Множество возможных значений статистического критерия, при которых нулевая гипотеза принимается, называется областью принятия.
Множество возможных значений статистического критерия, при которых нулевая гипотеза отвергается, называется критической областью.
Точки, разграничивающие критическую область и область принятия гипотезы, называются критическими точками.
При проверке статистических гипотез возникают следующие виды ошибок:
· ошибка первого рода – это вероятность отвергнуть правильную нулевую гипотезу;
· ошибка второго рода – это вероятность принять неправильную нулевую гипотезу.
Уровень значимости (р)- это максимально приемлемая для исследователя вероятность ошибочно отклонить нулевую гипотезу, когда на самом деле она верна, т.е. допускаемая исследователем величина ошибки первого рода.
При иссследованиях в фармации, медицине и биологии используется величина уровня значимости, равная 0,05. При разработке стандартов используют уровень значимости равный 0,01.
Уровень значимости или вероятность ошибки первого рода обозначается через «р», а вероятность ошибки второго рода - через «γ».
Доверительная вероятность (γ) - это вероятность не совершить ошибку первого рода и принять верную гипотезу Н0 (γ=1-р).
Важнейшей характеристикой любого статистического критерия является его мощность. Мощностью критерия называется его способность правильно исключать ложную гипотезу.
Мощность оценивается вероятностью 1-γ, где γ - вероятность ошибки второго рода.
Схема проверки статистических гипотез:
1) Выдвигаются две гипотезы: основная (нулевая) «Н0» и альтернативная (конкурирующая) «Н1».
2) Задается уровень значимости «р». Статистический вывод никогда не может быть сделан со стопроцентной уверенностью. Всегда допускается риск принятия неправильного решения.
При проверке статистических гипотез мерой такого риска является уровень значимости «р».
3) По исходным данным, т.е. по выборке, вычисляется наблюдаемое (эмпирическое, расчетное) значение критерия.
4) По специальным статистическим таблицам определяется табличное (критическое) значение критерия.
5) Путем сравнения наблюдаемых и табличных значений делается вывод о правильности той или иной гипотезы.
Все предположения о характере того или иного распределения - являются гипотезами. Поэтому они должны подвергаться статистической проверке с помощью критериев согласия. Эти критерии дают возможность определить, когда расхождения между теоретическими и эмпирическими частотами следует признать несущественными, т.е. случайными, а когда – существенными, т.е. неслучайными.
Схема применения критерия согласия χ2 -Пирсона:
6) Н0: случайная величина «Х» имеет функцию распределения F(x).
H1: случайная величина «Х» не имеет функцию распределения F(x).
7) р=0,05- уровень значимости.
8) 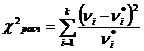 , (5.1)
, (5.1)
где k - число групп, на которое разбито эмпирическое распределение, 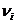 - наблюдаемая частота признака в i-й группе,
- наблюдаемая частота признака в i-й группе, 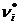 - теоретическая частота.
- теоретическая частота.
Для вычисления теоретических частот 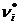 , нужно определить вероятности попадания случайной величины в интервал [xi, xi+1], используя формулу:
, нужно определить вероятности попадания случайной величины в интервал [xi, xi+1], используя формулу:
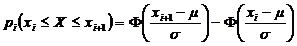 , (5.2)
, (5.2)
где µ - математическое ожидание, σ - среднее квадратическое отклонение, Ф(х) – функция распределения нормированного нормального распределения, [см. Приложение 1].
Если «µ»и «σ» неизвестны, то нужно вычислять их оценки 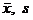 .
.
Заполнить таблицу, в последнем столбце подсчитать сумму, это и будет 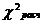 .
.
| Интервал [xi, xi+1] | Относительные частоты νi | Вероятности pi | Теоретические частоты 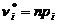
| 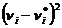
| 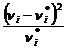
|
9) χ2табл (  ) , [см. Приложение 2],
) , [см. Приложение 2],
где 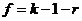 - число степеней свободы, k - число групп выборки, r - число параметров предполагаемого распределения (для нормального распределения r=2).
- число степеней свободы, k - число групп выборки, r - число параметров предполагаемого распределения (для нормального распределения r=2).
10) Если 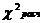 ≤
≤ 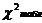 , то «H0» принимается.
, то «H0» принимается.
Если 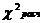 >
> 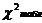 , то «H0» отвергается.
, то «H0» отвергается.
Критерий согласия Пирсона применяется при большом числе наблюдений (n>30), при этом частота каждой группы должна быть не менее пяти.
Схема применения критерия согласия Колмогорова - Смирнова:
6) Н0: случайная величина «Х» имеет функцию распределения F(x).
H1: случайная величина «Х» не имеет функцию распределения F(x).
7) р=0,05- уровень значимости.
8) 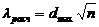 , (5.3)
, (5.3)
где 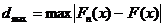 - максимальное значение абсолютной величины разности между наблюдаемой функцией распределения Fn(x) и соответствующей теоретической функцией распределения F(x).
- максимальное значение абсолютной величины разности между наблюдаемой функцией распределения Fn(x) и соответствующей теоретической функцией распределения F(x).
Для вычисления значений теоретической функции распределения для нормального распределения нужно использовать формулу
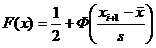 , (5.4)
, (5.4)
где 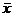 - выборочное среднее, s - среднее квадратическое отклонение, Ф(х) – функция Лапласа, [см. Приложение 3].
- выборочное среднее, s - среднее квадратическое отклонение, Ф(х) – функция Лапласа, [см. Приложение 3].
Заполнить таблицу, в последнем столбце найти максимальное значение, это и будет 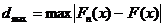 .
.
| Интервал [xi, xi+1] | Частоты νi | Накопленные частоты νi, накопл | 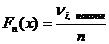
| F(x) | 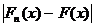
|
9) λтабл=1,36 (табличное значение при р=0,05).
10) Если 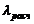 ≤
≤ 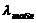 , то «H0» принимается.
, то «H0» принимается.
Если 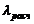 >
> 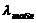 , то «H0» отвергается.
, то «H0» отвергается.
Критерий Колмогорова-Смирнова применяется при большом числе наблюдений (n>30).
Сравнение дисперсий двух нормальных генеральных совокупностей.
Даны две нормальные генеральные совокупности «Х» и «Y», дисперсии которых D(X) и D(Y) неизвестны.
По выборкам X1, X2,…, Xn и Y1, Y2,…, Ym объемов «n» и «m» соответственно требуется сравнить дисперсии.
Подобные сравнения возникают в случаях сравнения точности измерений, точности приборов, сравнения методик.
1) Н0: D(X) = D(Y).
H1: D(X) ≠ D(Y).
2) р=0,05- уровень значимости.
3) Fрасч.= 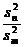 . (5.5)
. (5.5)
Примечание: в числителе нужно ставить большую из данных оценок, а в знаменателе меньшую.
4) Fтабл. ( 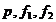 ) [см. Приложение 4],
) [см. Приложение 4],
где f1=n-1, f2=m-1 - число степеней свободы.
5) Если 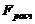 ≤
≤ 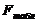 , то «H0» принимается.
, то «H0» принимается.
Если 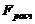 >
> 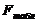 , то «H0» отвергается.
, то «H0» отвергается.
Проверка гипотезы о равенстве неизвестной дисперсии конкретному значению.
Генеральная совокупность «Х» имеет нормальное распределение. Дисперсия генеральной совокупности известна, она равна определенному числу: D(X)= 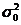 .
.
Требуется проверить указанное предположение.
Подобные сравнения применяются в практике для оценки точности измерительных приборов, устойчивости методов исследования, стабильности протекания различных процессов, характеризующихся численными показателями.
1) Н0: М(S2) = 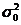 .
.
H1: М(S2)> 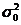 .
.
2) р=0,05- уровень значимости.
3) χ2расч.= 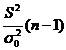 . (5.6)
. (5.6)
4) χ2табл. (p, f) [см. Приложение 2],
где 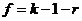 - число степеней свободы, k - число групп выборки, r - число параметров предполагаемого распределения (для нормального распределения r=2).
- число степеней свободы, k - число групп выборки, r - число параметров предполагаемого распределения (для нормального распределения r=2).
5) Если 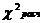 ≤
≤ 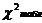 , то «H0» принимается.
, то «H0» принимается.
Если 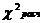 >
> 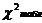 , то «H0» отвергается.
, то «H0» отвергается.
6. Литература:
1. Гланц С. Медико-биологическая статистика. Пер. с англ.-М.: Практика, 1998. - 459 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов / В.Е. Гмурман. - М.: Высшая школа, 2003. - 479 с.
3. Лобоцкая Н.Л. Высшая математика. / Н.Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. - Мн.: Высшая школа, 1987. - 319 с.
4. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах / Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
5. Основы высшей математики и математической статистики: Учебник / И.В. Павлушков и соавт. - М.: ГЭОТАР-МЕД, 2004. - 424 с.
6. Петри А., Сэбин К. Наглядная медицинская статистика /А. Петри, К. Сэбин; пер. с англ. - М.: ГЭОТАР-Медиа, 2009. - 168 с.
7. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие / ред. Кучеренко В.З. - М.: ГЭОТАР-Медиа, 2011. - 256 с.
8. http://matstats.ru/
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №6
1. Тема: Проверка гипотез о параметрах нормально распределенных совокупностей. t-критерий Стьюдента для анализа биомедицинских данных. Реализация t-критерия Стьюдента в программе «Statistica».
2. Цель: Изучение методических основ, условий применения и реализации в программе «Statistica» t-критерия Стьюдента.
3. Задачи обучения: Сформировать навыки постановки, проверки статистических гипотез при использовании t-критерия Стьюдента и реализации этого критерия в программе «Statistica».
4. Основные вопросы темы:
1. Какова общая постановка задачи, для которой может быть использован критерий Стьюдента?
2. Как формулируется нулевая гипотеза при использовании критерия Стьюдента?
3. В чем разница между двухвыборочным и парным критерием Стьюдента?
4. Какова схема применения двухвыборочного критерия Стьюдента?
5. Какова схема применения парного критерия Стьюдента?
6. Почему критерий Стьюдента находит широкое применение при анализе медико-биологических данных?
7. Какими способами можно реализовать t-критерий Стьюдента в программе«Statistica»?
5. Методы обучения и преподавания: письменное решение задач, статистическая обработка материалов с помощью компьютерной программы «Statistica 10».
v Задания:
1. Ознакомиться с краткой теорией практического занятия №6.
2. Ответить на основные вопросы темы.
3. Выполнить примеры 6.1, 6.2.
4. Ученые определили среднее артериальное давление и общее периферическое сосудистое сопротивление при операциях на открытом сердце с галотановой (9 больных) и морфиновой (16 больных) анестезией. Были получены следующие данные.
| Показатель | Галотан (n=9) | Морфин (n=16) | ||
| Среднее | Стандартное отклонение | Среднее | Стандартное отклонение | |
| Среднее артериальное давление при наилучшем сердечном индексе, мм рт. ст. | 76,8 | 13,8 | 91,4 | 19,6 |
| Общее периферическое сосудистое сопротивление при наилучшем сердечном индексе, дин с см-5 | 2210 | 1200 | 2830 | 1130 |
Можно ли утверждать, что в группах галотановой и морфиновой анестезии эти гемодинамические показатели различаются статистически значимо?
Указание: проверить решение задачи с помощью программы «Statistica 10».
5. Кокаин очень вреден для сердца, он может вызвать инфаркт миокарда даже у молодых людей без атеросклероза. Кокаин сужает коронарные сосуды и это приводит к уменьшению притока крови к миокарду. Кокаин ухудшает сокращательную способность сердца. Препарат «нифедипин» обладает способностью расширять сосуды. Его применяют при ишемической болезни сердца. Ученые предположили, что нифедипин можно использовать и при деструкции сердца, вызванной кокаином. Собакам вводили кокаин, а затем нифедипин или физиологический раствор. Показателем сокращательной способности сердца служило среднее артериальное давление. Были получены следующие данные.
| Среднее артериальное давление после приема кокаина, мм. рт. ст. | |
| Физиологический раствор | Нифедипин |
| 156 | 73 |
| 171 | 81 |
| 133 | 103 |
| 102 | 88 |
| 129 | 130 |
| 150 | 106 |
| 120 | 106 |
| 110 | 111 |
| 112 | 122 |
| 130 | 108 |
| 105 | 99 |
Влияет ли нифедипин на среднее артериальное давление после приема кокаина?
Указание: проверить решение задачи с помощью программы «Statistica 10».
6. Ученые измеряли диаметр коронарной артерии после приема нифедипина и физиологического раствора. Были получены следующие данные.
| Диаметр коронарной артерии, мм | |
| Физиологический раствор | Нифедипин |
| 2,2 | 2,5 |
| 2,5 | 1,7 |
| 2,6 | 1,5 |
| 2,0 | 2,5 |
| 2,1 | 1,4 |
| 1,8 | 1,9 |
| 2,4 | 2,3 |
| 2,3 | 2,0 |
| 2,7 | 2,6 |
| 2,7 | 2,3 |
| 1,9 | 2,2 |
Влияет ли нифедипин на диаметр коронарной артерии?
Указание: проверить решение задачи с помощью программы «Statistica 10».
7. У студентов-медиков проводилось исследование пульса до и после сдачи экзамена. Частота пульса до экзамена составила 98,8 ±4,0, а после экзамена 84,0 ±5,0. Можно ли считать, что после экзаменов частота пульса снижается и приближается к норме?
8. У студентов-медиков проводилось исследование артериального давления до и после сдачи экзамена. Максимальное давление до сдачи экзамена составило 127,2±6,0, после сдачи 117±4,0 мм рт. ст. Можно ли считать, что до сдачи экзаменов у студентов действительно имеется повышение максимального артериального давления?
9. Содержание холестерина в сыворотке крови у больных с коронарным атеросклерозом составило 231,0±4,0 мг% до применения холина и 204,0±3,0 мг% после лечения. Можно ли считать, что применение холина снижает содержание холестерина в сыворотке крови?
10. Сравнить результаты выполнения логических задач до и после курса обучения. Исходные данные представлены в таблице.
| № | Результаты выполнения логических задач до курса (сек.) | Результаты выполнения логических задач после курса (сек.) |
| 1 | 25 | 22 |
| 2 | 23 | 25 |
| 3 | 28 | 23 |
| 4 | 29 | 22 |
| 5 | 35 | 30 |
| 6 | 31 | 27 |
| 7 | 24 | 20 |
| 8 | 24 | 19 |
| 9 | 38 | 32 |
| 10 | 26 | 25 |
| 11 | 20 | 20 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
v Краткая теория
t-критерий Стьюдента - метод проверки однородности выборок, позволяет принять или отвергнуть гипотезу о равенстве средних двух выборок ( 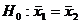 ).
).
t-критерий Стьюдента используется:
· при проверке гипотезы о равенстве средних двух независимых выборок (двухвыборочный t-критерий). Вэтом случае анализируются контрольная и экспериментальная выборки разных объемов. Например, группа больных сахарным диабетом и группа здоровых людей;
· при проверке гипотезы о равенстве средних двух зависимых выборок (парный t-критерий). В этом случае анализируется одна и та же выборка, но до и после эксперимента.Например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата.
Применение критерия Стьюдента возможно, если выполняются следующие два условия:
1) рассматриваемые выборки имеют нормальное распределение;
2) дисперсии рассматриваемых выборок равны.
Схема применения двухвыборочного критерия Стьюдента:
1) Н0: 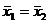 .
.
Н1: 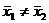 .
.
3) р=0,05- уровень значимости.
4) 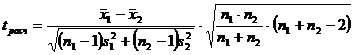 , (6.1)
, (6.1)
где n1, n2 - объемы рассматриваемых выборок, 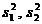 - дисперсии рассматриваемых выборок,
- дисперсии рассматриваемых выборок, 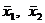 - сравниваемые средние значения выборок.
- сравниваемые средние значения выборок.
4) 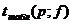 , [см. Приложение 5],
, [см. Приложение 5],
где f= n1+n2-2- число степеней свободы.
5) Если 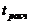 ≤
≤ 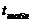 , то «H0» принимается.
, то «H0» принимается.
Если 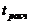 >
> 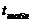 , то «H0» отвергается.
, то «H0» отвергается.
Критерий Стьюдента применяется в случае малых выборок (n1,2≤30).
Схема применения парного критерия Стьюдента:
1) Н0: 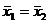 .
.
Н1: 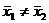 .
.
4) р=0,05- уровень значимости.
5) 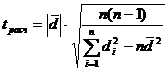 , (6.2)
, (6.2)
где 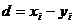 - разности между соответствующими значениями пар переменных,
- разности между соответствующими значениями пар переменных, 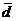 - среднее значение этих разностей, n - объем выборки.
- среднее значение этих разностей, n - объем выборки.
4)  , [см. Приложение 5],
, [см. Приложение 5],
где f= n-1- число степеней свободы.
5) Если 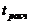 ≤
≤ 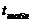 , то «H0» принимается.
, то «H0» принимается.
Если 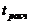 >
> 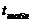 , то «H0» отвергается.
, то «H0» отвергается.
Иногда сравнение выборочных средних проводится по следующей формуле:
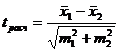 , (6.3)
, (6.3)
где 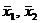 - сравниваемые средние величины; m1 и m2 - ошибки сравниваемых средних величин.
- сравниваемые средние величины; m1 и m2 - ошибки сравниваемых средних величин.
Если tрасч³2, то «H0» отвергается.
Реализация t-критерия Стьюдента в программе «Statistica».
t-критерий Стьюдента для независимых выборок
В программе «Statistica» есть два варианта критерия Стьюдента для сравнения независимых выборок:
1 - для анализа исходных данных в таблице данных;
2 - для анализа с использованием ранее рассчитанных значений средних, среднего квадратического отклонения и числа объектов исследования при условии, что оба условия t-критерия выполнены.
Пример 6.1. Сравнить результаты выполнения тестов в двух группах. Исходные данные представлены в таблице.
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 46 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Создать таблицу данных «Результаты тестирования» размером 2*58 в программе «Statistica», внести исходные данные.
Выбрать Statistics→Basic Statistics→t-test independent by groups (t-критерий для независимых выборок) (рисунок 6.1).
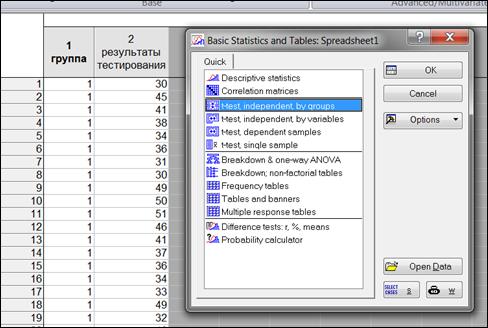
Рисунок 6.1. Выбор процедуры «t-test independent by groups»
В диалоговом окне, нажать кнопку «Variables» (Переменные), указать в правой части окна группирующий признак (столбец, содержащий коды групп), а в левой части окна – столбец, содержащий анализируемый признак (рисунок 6.2), нажать кнопку «OK».
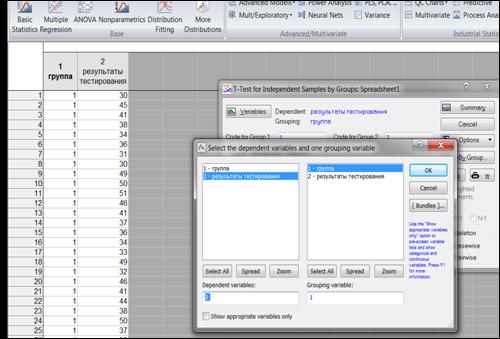
Рисунок 6.2. Задание переменных
Проверка первого условия применимости критерия Стьюдента (нормальность распределения признаков).
Выбрать вкладку «Advanced» (Дополнительно), здесь имеются кнопки «Categorized normal plots» (Категоризированные нормальные графики) и «Categorized histograms» (Категоризированная гистограмма).
Построив эти графики можно сделать вывод о нормальности распределения (рисунок 6.3).
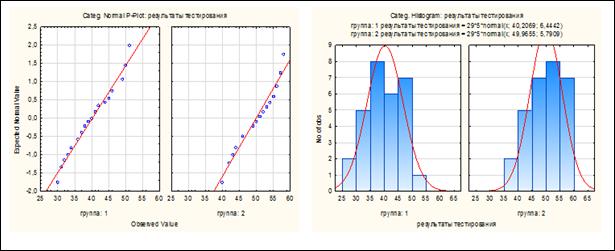
Рисунок 6.3. Проверка признаков на нормальность распределения
Для проверки выполнения второго условия применимости критерия Стьюдента (равенство дисперсий распределений признаков) программа автоматически использует F-критерий Фишера.
Или можно воспользоваться процедурой расчета критерия Левина, для чего необходимо выбрать опцию «Options/Levene’s test» (рисунок 6.4).
Рисунок 6.4. Выбор опции «Levene’s test» (Критерий Левина)
После нажатия кнопки «Summary» на экране появится итоговая таблица с результатами сравнения двух независимых выборок по t-критерию Стьюдента (рисунок 6.5).
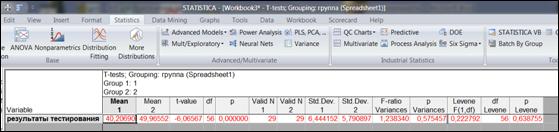
Рисунок 6.5. Итоговая таблица с результатами сравнения двух независимых выборок по t-критерию Стьюдента
Наименование столбцов итоговой таблицы:
- Mean 1, Mean 2 – средние значения переменных;
- t-value – значение t-критерия;
- df – число степеней свободы;
- р – уровень значимости t-критерия;
- Valid 1, Valid 2 - число наблюдений в группах;
- Std. Dev. – стандартные отклонения значений переменных;
- F-ratio Variances – значение F- критерия;
- p Variances - уровень значимости F-критерия;
- Levene F(1,df) – значение критерия Левина;
- df Levene - число степеней свободы критерия Левина;
- р Levene - уровень значимости критерия Левина.
Если для критерия Левина р<0,05, следует сделать вывод о различии дисперсий в сравниваемых группах.
Если для критерия Левина р>0,05, следует сделать вывод о равенстве дисперсий в сравниваемых группах.
Аналогично для F-критерия:
Если для t-критерия значение р>0,05, то нулевая гипотеза о равенстве средних принимается.
Если для t-критерия значение р<0,05 (такие результаты выделяются красным цветом шрифта), то нулевая гипотеза о равенстве средних отклоняется.
Если среднее и среднее квадратическое отклонение были рассчитаны в ходе предыдущего анализа, а также известно, что выполняются условия применимости t-критерия, можно использовать другую процедуру программы «Statistica».
Выберем Statistics→Basic Statistics→Difference tests: r, %, means (Другие тесты).
Подставив соответствующие параметры для каждой из двух групп в диалоговое окно и выполнив расчет, получим значение «р» (рисунок 6.6).
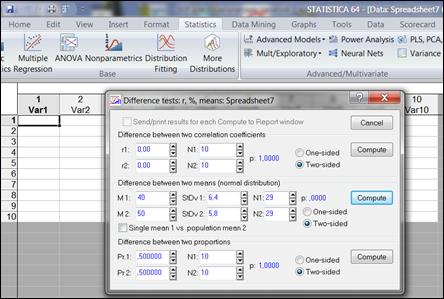
Рисунок 6.6. Диалоговое окно процедуры «Difference tests: r, %, means»
Полученные результаты можно интерпретировать следующим образом:
· если р>0,05, то нулевая гипотеза об отсутствии различий средних принимается;
· если р<0,05, то нулевая гипотеза отклоняется.
t-критерий Стьюдента для зависимых выборок
Использование t-критерия для зависимых выборок возможно если распределения признаков в каждом из сопоставляемых столбцов нормальные, а дисперсии равны.
Поэтому, перед применением t-критерия, необходимо проверить гипотезу о том, что распределения признака в каждом из сравниваемых столбцов являются нормальными.
Рассмотрим другой способ проверки нормальности распределений. Порядок выбора: Statistics→Basic statistics→Descriptive statistics→Normality. Проверку на нормальность можно провести с помощью «Kolmogorov-Smirnov & Lilliefors test of normality» (критерия на нормальность Колмогорова-Смирнова и Лиллиефорса) или «Shapiro-Wilk’s W test» (W-критерия Шапиро-Уилка). Для этого нужно выбрать соответствующие опции и нажать кнопку «Histograms» (Гистограмма).
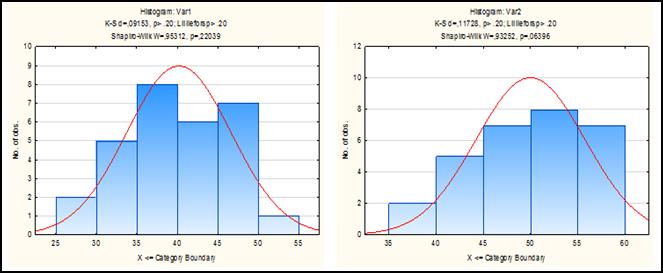
Рисунок 6.7. Проверка на нормальность распределений признаков
На появившихся гистограммах (рисунок 6.7) вверху приведены результаты тестов на нормальность, которые можно пояснить следующим образом:
· если в данных тестах р>0,05, то гипотеза о нормальном распределении принимается;
· если р<0,05, то гипотеза о нормальном распределении отвергается.
Итак, для проверки нулевой гипотезы об отсутствии различий в зависимых группах с помощью t-критерия Стьюдента выбрать: Statistics→Basic statistics→t-test dependent samples (t-критерий для зависимых выборок) (рисунок 6.8).
Задать переменные «Variables».
После нажатия кнопки «Summary» на экране появится итоговая таблица (рисунок 6.9).
Полученные результаты можно интерпретировать следующим образом:
· если р<0,05, то нулевая гипотеза отклоняется (такие результаты выделяются красным цветом шрифта);
· если р>0,05, то нулевая гипотеза принимается.
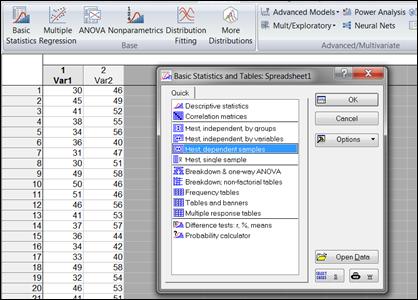
Рисунок 6.8. Выбор процедуры «t-test dependent samples»

Рисунок 6.9. Итоговая таблица с результатами сравнения двух зависимых выборок по t-критерию Стьюдента
6. Литература:
1. Гланц С. Медико-биологическая статистика. Пер. с англ.-М.: Практика, 1998. - 459 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов / В.Е. Гмурман. - М.: Высшая школа, 2003. - 479 с.
3. Лобоцкая Н.Л. Высшая математика. / Н.Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. - Мн.: Высшая школа, 1987. - 319 с.
4. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах / Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
5. Основы высшей математики и математической статистики: Учебник / И.В. Павлушков и соавт. - М.: ГЭОТАР-МЕД, 2004. - 424 с.
6. Петри А., Сэбин К. Наглядная медицинская статистика /А. Петри, К. Сэбин; пер. с англ. - М.: ГЭОТАР-Медиа, 2009. - 168 с.
7. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие / ред. Кучеренко В.З. - М.: ГЭОТАР-Медиа, 2011. - 256 с.
8. http://matstats.ru/
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №7
1. Тема: Непараметрические критерии проверки статистических гипотез. Критерий Манна-Уитни, критерий Уилкоксона. Назначение, алгоритмы вычисления и ограничения.
2. Цель: Изучение методических основ, условий применения и реализации в программе «Statistica» критерия Манна-Уитни и критерия Уилкоксона.
3. Задачи обучения: Сформировать навыки постановки и проверки статистических гипотез при использовании критерия Манна-Уитни и критерия Уилкоксона. Сформировать навыки реализации этих критериев в программе «Statisticа».
4. Основные вопросы темы:
1. Какие статистические критерии называются непараметрическими?
2. Каково назначение U-критерия Манна-Уитни?
3. Почему данный критерий называют непараметрическим аналогом двухвыборочного t-критерия Стьюдента?
4. Каковы ограничения для U-критерия Манна-Уитни?
5. Какова схема применения U-критерия Манна-Уитни?
6. Каково назначение W-критерия Уилкоксона?
7. Почему данный критерий называют непараметрическим аналогом парного t-критерия Стьюдента?
8. Каковы ограничения для W-критерия Уилкоксона?
9. Какова схема применения W-критерия Уилкоксона?
10. Как реализуется U-критерий Манна-Уитни в программе«Statistica»?
11. Как реализуется W-критерий Уилкоксона в программе«Statistica»?
5. Методы обучения и преподавания: письменное решение задач, статистическая обработка материалов с помощью компьютерной программы «Statistica 10».
v Задания:
1. Ознакомиться с краткой теорией практического занятия №7.
2. Ответить на основные вопросы темы.
3. Выполнить примеры 7.1, 7.2.
4. С помощью U-критерия Манна-Уитни сравнить уровень интеллекта студентов в двух группах. Исходные данные приведены в таблице.
| 1 группа | 2 группа | ||
| Ф.И.О. испытуемого | Баллы IQ | Ф.И.О. испытуемого | Баллы IQ |
| КТИ | 112 | БРИ | 121 |
| ВСИ | 105 | ДРО | 120 |
| МНИ | 109 | РНА | 134 |
| АНМ | 90 | ВРА | 119 |
| УРА | 130 | ГРА | 115 |
| ВФА | 117 | ДЖА | 106 |
| РКИ | 117 | ВКК | 107 |
| ТРИ | 125 | ЮАР | 101 |
| ТРК | 134 | ЖЕН | 97 |
| ТНК | 109 | КОР | 117 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
5. С помощью U-критерия Манна-Уитни сравнить продолжительность бодрствования в первый час жизни младенцев, рожденных по обычной и методике Лебуайе. Исходные данные приведены в таблице.
| Роды по обычной методике | Роды по методике Лебуайе |
| 5,0 | 2,0 |
| 10,1 | 19,0 |
| 17,7 | 29,7 |
| 20,3 | 32,1 |
| 22,0 | 35,4 |
| 24,9 | 36,7 |
| 26,5 | 38,5 |
| 30,8 | 40,2 |
| 34,2 | 42,1 |
| 35,0 | 43,0 |
| 36,6 | 44,4 |
| 37,9 | 45,6 |
| 40,4 | 46,7 |
| 45,5 | 47,1 |
| 49,3 | 48,0 |
| 51,1 | 49,0 |
| 53,1 | 50,9 |
| 55,0 | 51,2 |
| 56,7 | 52,5 |
| 58,0 | 53,3 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
6. Изучается систолическое артериальное (САД) давление (в мм. рт. ст.) в двух однородных группах здоровых мужчин:
· группа 1 - лицас многолетним стажем работы в условиях нарушенного режима сна и бодрствования (работа, связанная с ночными дежурствами);
· группа 2 - лица без нарушения суточного ритма сна и бодрствования.
Требуется оценить значимость различия систолического артериального давления в двух независимых группах по критерию U-Манна-Уитни.
Исходные данные приведены в таблице.
| № | Группа | САД | № | Группа | САД |
| 1 | 1 | 90 | 12 | 2 | 110 |
| 2 | 1 | 95 | 13 | 2 | 115 |
| 3 | 1 | 100 | 14 | 2 | 115 |
| 4 | 1 | 105 | 15 | 2 | 122 |
| 5 | 1 | 120 | 16 | 2 | 122 |
| 6 | 1 | 135 | 17 | 2 | 125 |
| 7 | 1 | 135 | 18 | 2 | 125 |
| 8 | 1 | 135 | 19 | 2 | 130 |
| 9 | 1 | 140 | 20 | 2 | 150 |
| 10 | 1 | 140 | |||
| 11 | 1 | 145 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
7. Определяется содержание сиаловой кислоты (в единицах) в крови больных инфарктом миокарда, поступивших на стационарное лечение в срок до 3 дней (группа 1-7 человек) и позднее 6 дней (группа 2-12 человек) от начала заболевания. Требуется оценить значимость различия содержания сиаловой кислоты в двух независимых группах по критерию U-Манна-Уитни.
Исходные данные представлены в таблице.
| № | Группа | Сиаловая кислота | № | Группа | Сиаловая кислота |
| 1 | 1 | 240 | 11 | 2 | 226 |
| 2 | 1 | 235 | 12 | 2 | 230 |
| 3 | 1 | 270 | 13 | 2 | 305 |
| 4 | 1 | 280 | 14 | 2 | 278 |
| 5 | 1 | 185 | 15 | 2 | 210 |
| 6 | 1 | 287 | 16 | 2 | 228 |
| 7 | 1 | 148 | 17 | 2 | 335 |
| 8 | 2 | 314 | 18 | 2 | 305 |
| 9 | 2 | 270 | 19 | 2 | 335 |
| 10 | 2 | 220 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
8. С помощью U-критерия Манна-Уитни сравнить два метода определения времени свертываемости крови. Каждая проба оценивается двумя методами:
· по Бюркеру - появление нитей фибрина при комнатной температуре;
· по Ли-Уайту - при опрокидывании пробирки в термостате при 37оС кровь не выливается.
Исходные данные представлены в таблице.
| № | по Бюркеру | по Ли-Уайту |
| 1 | 10 | 10 |
| 2 | 9 | 8 |
| 3 | 8 | 9 |
| 4 | 8 | 10 |
| 5 | 7 | 6 |
| 6 | 7 | 10 |
| 7 | 5 | 6 |
| 8 | 5 | 6 |
| 9 | 6 | 7 |
| 10 | 6 | 7 |
| 11 | 7 | 9 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
9. С помощью W-критерия Уилкоксонапроверить эффективность специальной диеты, позволяющей избавиться от избыточного веса. Исходные данные представлены в таблице.
| № | Масса (кг) до эксперимента | Масса (кг) после эксперимента |
| 1 | 93,2 | 88,9 |
| 2 | 98,2 | 94,5 |
| 3 | 105,6 | 106,1 |
| 4 | 86,8 | 84,3 |
| 5 | 95,5 | 92,5 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
10. С помощью W-критерия Уилкоксонапроверить влияет ли курение на функцию тромбоцитов. Исходные данные приведены в таблице.
| № | Агрегация тромбоцитов | |
| До курения | После курения | |
| 1 | 25 | 27 |
| 2 | 25 | 29 |
| 3 | 27 | 37 |
| 4 | 44 | 56 |
| 5 | 30 | 46 |
| 6 | 67 | 82 |
| 7 | 53 | 57 |
| 8 | 53 | 80 |
| 9 | 52 | 61 |
| 10 | 60 | 59 |
| 11 | 28 | 43 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
11. С помощью W-критерия Уилкоксонапроверить является ли некий исследуемый препарат диуретиком.Исходные данные приведены в таблице.
| № | Суточный диурез, мл | |
| До приема препарата | После приема препарата | |
| 1 | 1490 | 1600 |
| 2 | 1300 | 1850 |
| 3 | 1400 | 1300 |
| 4 | 1410 | 1500 |
| 5 | 1350 | 1400 |
| 6 | 1000 | 1010 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
v Краткая теория
Статистические критерии делятся на параметрические и непараметрические.
Параметрические критерии предполагают наличие нормального распределения в сравниваемых выборках и используют в процессе расчета параметры распределения (средние, дисперсии, СКО) (например, t-критерий Стьюдента, F-критерий Фишера и др.).
Непараметрические критерии не предполагают нормального распределения в сравниваемых выборках и используют в процессе расчета ранги значений признака (например, критерий Манна-Уитни, критерий Уилкоксона, критерий знаков и др.).
Ранг - порядковый номер значения признака.
Для каждого параметрического критерия имеется, по крайней мере, один непараметрический аналог.
Аналогом двухвыборочного t-критерия Стьюдента является U-критерий Манна-Уитни. Аналогом парного t-критерия Стьюдента является W-критерий Уилкоксона.
U-критерий Манна-Уитни - непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно.
U-критерий подходит для сравнения малых выборок: в каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было 2 значения, но во второй тогда должно быть не менее пяти (n1, n2≥3 или n1=2, n2≥5).
Условием для применения U-критерия Манна-Уитни является отсутствие в сравниваемых группах совпадающих значений признака (все числа разные) или очень малое число таких совпадений.
W-критерий Уилкоксона - непараметрический статистический критерий, используемый для сравнения двух зависимых выборок по уровню какого-либо признака, измеренного количественно.
Критерий Уилкоксона применяется в случае, если объем выборки n удовлетворяет неравенству 5≤n≤50.
Схема применения критерия Манна-Уитни:
1) Н0: 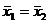 .
.
Н1: 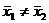 .
.
6) р=0,05 - уровень значимости.
7) Из двух сравниваемых выборок составляется единый ранжированный ряд.
Единый ранжированный ряд разделяется на два, состоящих из единиц первой и второй выборок, при этом отмечаются значения рангов для каждой единицы.
Подсчитывается отдельно сумма рангов, выпавших на долю элементов первой выборки, и отдельно - на долю элементов второй выборки.
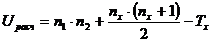 , (7.1)
, (7.1)
где Tx - большая из двух ранговых сумм, nx - объем выборки, соответствующий Tx, n1, n2 - объемы рассматриваемых выборок.
8) Uтабл (  ),[см. Приложение 6].
),[см. Приложение 6].
9) Если  >
>  , то «H0» принимается.
, то «H0» принимается.
Если 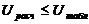 , то «H0» отвергается.
, то «H0» отвергается.
Схема применения критерия Уилкоксона:
1) Н0: 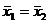 .
.
Н1: 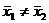 .
.
2) р≈0,05 - уровень значимости.
3) Вычисляется разность между индивидуальными значениями во втором и первом замерах.
Абсолютные величины разностей ранжируются, причем меньшему значению присваивается меньший ранг.
Каждому рангу ставится знак «+» или «–» в зависимости от знака соответствующей ему разности, получаются знаковые ранги.
Расчетное значение статистики критерия Wрасч определяется из суммы знаковых рангов.
4)Wтабл ( 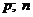 ), [см. Приложение 7],
), [см. Приложение 7],
где n - объем выборки.
5) Если 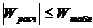 , то «H0» принимается.
, то «H0» принимается.
Если 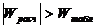 , то «H0» отвергается.
, то «H0» отвергается.
Реализация критерия Манна-Уитни в программе «Statistica».
Пример 7.1. Исследуется эффективность препарата, позволяющего сбросить лишнюю массу больным, страдающим ожирением. При этом группе добровольцев предписана определенная диета.
Через месяц, с целю проверки соблюдения диеты и регулярного приема препарата, фиксируется величина потерянной массы (кг). Для проведения эксперимента отобрана группа из 8 человек. 3 из них получали исследуемый препарат (экспериментальная группа), а 5 получали плацебо (контрольная группа). Отбор 3 испытуемых из 8 в экспериментальную группу осуществлялся случайным образом. Все участники эксперимента считали, что принимают препарат.
| Экспериментальная группа | Контрольная группа |
| Потерянная масса, кг | Потерянная масса, кг |
| 6,2 | 4,0 |
| 3,0 | -0,5 |
| 3,9 | 3,3 |
| 1,5 | |
| 3,0 |
Создать таблицу данных «Эффективность препарата» в программе «Statistica» размером 2*8 и внести исходные данные.
Выбрать Statistics→Nonparametrics (Непараметрические) (рисунок 7.1)→Comparing two independent samples (groups) (Сравнение двух независимых выборок (групп)) (рисунок 7.2), нажатькнопку «OK».
Рисунок 7.1. Выбор модуля «Nonparametrics»
Рисунок 7.2. Выбор процедуры «Comparing two independent samples (groups)»
В диалоговом окне, нажать кнопку «Variables» (Переменные), указать в правой части окна группирующий признак (столбец, содержащий коды групп), а в левой части окна – столбец, содержащий анализируемый признак (рисунок 7.3) и нажать кнопку «OK».
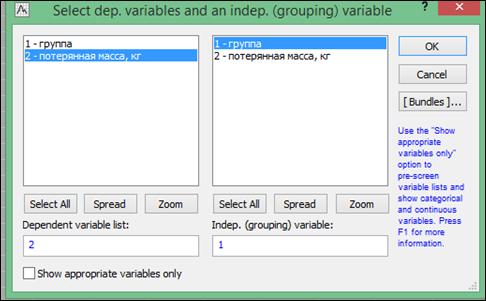
Рисунок 7.3. Задание переменных
В диалоговом окне нажать кнопку «Mann-Whitney U test».
На экране появится итоговая таблица (рисунок 7.4).
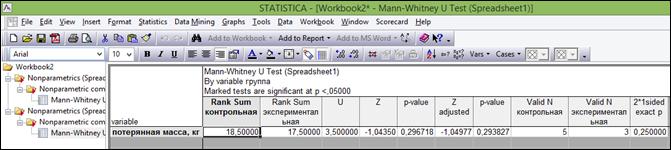
Рисунок 7.4. Итоговая таблица с результатами сравнения двух независимых выборок по критерию Манна-Уитни
В первом и втором столбцах указаны суммы рангов (Rank Sum).
Если р > 0,05, то нулевая гипотеза принимается.
Если р < 0,05, то нулевая гипотеза отвергается (такие результаты выделяются красным цветом шрифта).
В данном примере р=0,296718 и р=0,293827, значит гипотеза о равенстве средних принимается, т.е. препарат неэффективен.
Для нагладности можно построить график «ящик с усами», нажав в окне анализа кнопку «Box & whisker plots for all variables» (рисунок 7.5).
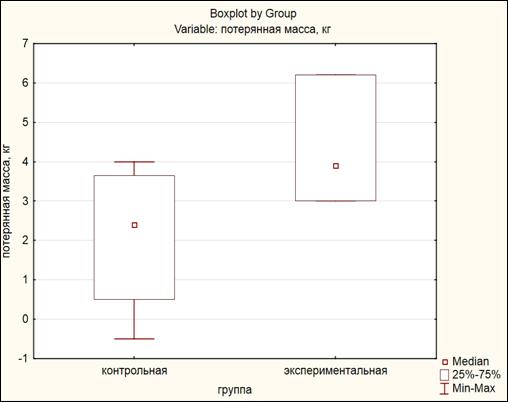
Рисунок 7.5. График «ящик с усами».
Реализация критерия Уилкоксона в программе «Statistica».
Пример 7.2. Проверить есть ли разница в содержании сахара в крови натощак до работы и через три часа после работы у 12 работающих на ультразвуковых установках.
| № | Содержание сахара до работы | Содержание сахара после работы |
| 1 | 112 | 54 |
| 2 | 82 | 67 |
| 3 | 101 | 96 |
| 4 | 72 | 59 |
| 5 | 79 | 79 |
| 6 | 82 | 76 |
| 7 | 64 | 66 |
| 8 | 70 | 66 |
| 9 | 88 | 48 |
| 10 | 81 | 50 |
| 11 | 66 | 61 |
| 12 | 88 | 61 |
Создать таблицу данных «Содержание сахара в крови» в программе «Statistica» размером 2*12 и внести исходные данные.
Выбрать Statistics→Nonparametrics (Непараметрические)→Comparing two dependent samples (variables) (Сравнение двух зависимых выборок (переменных)) (рисунок 7.6) и нажать кнопку «OK».
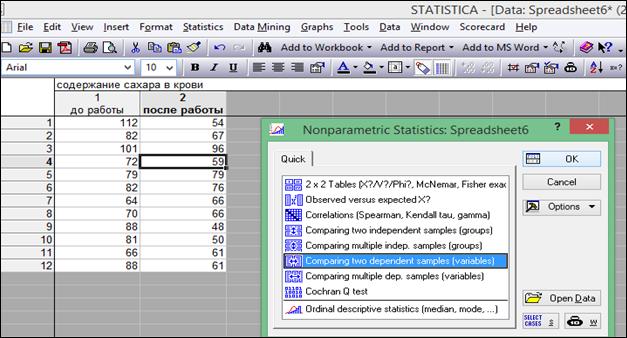
Рисунок 7.6. Выбор процедуры «Comparing two dependent samples (variables)»
В диалоговом окне, нажать кнопку «Variables» (Переменные), указать в левой части окна первую переменную, а в правой части окна – вторую переменную (рисунок 7.7) и нажать кнопку «OK».
Рисунок 7.7. Задание переменных
В диалоговом окне нажать кнопку «Wilcoxon matched pairs test».
На экране появится итоговая таблица (рисунок 7.8).

Рисунок 7.8. Итоговая таблица с результатами сравнения двух зависимых выборок по критерию Уилкоксона
Если р > 0,05, то нулевая гипотеза принимается.
Если р < 0,05, то нулевая гипотеза отвергается (такие результаты выделяются красным цветом шрифта).
В данном примере р=0,004439, значит нулевая гипотеза о равенстве средних отвергается, т.е. есть разница в содержании сахара в крови у работников до и после работы.
Для нагладности можно построить график «ящик с усами», нажав в окне анализа кнопку «Box & whisker plots for all variables» (рисунок 7.9).
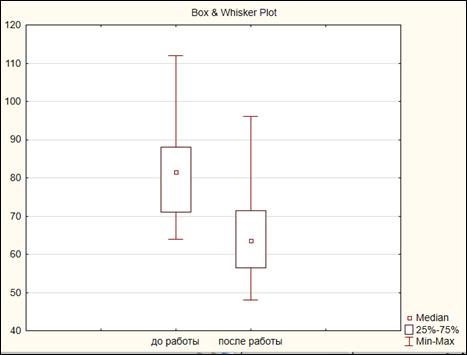
Рисунок 7.9. График «ящик с усами».
6. Литература:
1. Боровиков В.П. Популярное введение в программу STATISTICA. - М.: Компьютер Пресс, 1998. - 240 с.
2. Боровиков В.П. STATISTICA. Искусство анализа данных на компьютере: для профессионалов / В. Боровиков. - СПб.: Питер, 2004. - 688 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов.- 9-е изд., стер. - М.: Высш. шк., 2003. - 479 с.
4. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах/ Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
5. Реброва О.Ю. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA. - М.: МедиаСфера, 2002. - 312 с.
6. Халафян А.А. Statistica 6. Статистический анализ данных. 3-е изд. Учебник - М.: ООО «Бином-Пресс», 2007. - 512 с.
7. http://matstats.ru/
8. http://www.statsoft.ru/
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №8
1. Тема: Дисперсионный анализ. Статистические гипотезы, проверяемые с помощью дисперсионного анализа. Общая, факторная и остаточная дисперсии. Метод однофакторного и двухфакторного дисперсионного анализа. Непараметрический критерий Крускала-Уоллиса - аналог однофакторного дисперсионного анализа.
2. Цель: Изучение методических основ, условий применения и реализации в программе «Statistica» однофакторного и двухфакторного дисперсионного анализа, а также критерия Крускала-Уоллиса.
3. Задачи обучения: Сформировать навыки постановки и проверки статистических гипотез при использовании однофакторного и двухфакторного дисперсионного анализа. Сформировать навыки реализации дисперсионного анализа и критерия Крускала-Уоллиса в программе «Statistica».
4. Основные вопросы темы:
1. Какая нулевая гипотеза проверяется с помощью дисперсионного анализа?
2. Какие условия должны выполняться при использовании дисперсионного анализа?
3. Какова основная идея дисперсионного анализа?
4. Какова схема применения однофакторного дисперсионного анализа?
5. Когда используется H-критерий Крускала – Уоллиса?
6. Какова схема применения H-критерия Крускала – Уоллиса?
7. Как реализуется однофакторный и двухфакторный дисперсионный анализ в программе«Statistica»?
8. Как реализуется H-критерий Крускала–Уоллиса в программе«Statistica»?
5. Методы обучения и преподавания: письменное решение задач, статистическая обработка материалов с помощью компьютерной программы «Statistica 10».
v Задания:
1. Ознакомиться с краткой теорией практического занятия №8.
2. Ответить на основные вопросы темы.
3. Выполнить примеры 8.1, 8.2, 8.3.
4. Произведено по пять испытаний на каждом из четырех уровней фактора «F». Все четыре выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями. Результаты испытаний занесены в таблицу.
| Номер испытания i | Уровень фактора «F» | |||
| F1 | F2 | F3 | F4 | |
| 1 | 36 | 56 | 52 | 39 |
| 2 | 47 | 61 | 57 | 57 |
| 3 | 50 | 64 | 59 | 63 |
| 4 | 58 | 66 | 58 | 61 |
| 5 | 67 | 66 | 79 | 65 |
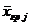
| 51,6 | 62,6 | 61,0 | 57,0 |
При уровне значимости 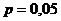 , методом дисперсионного анализа требуется проверить гипотезу о равенстве групповых средних.
, методом дисперсионного анализа требуется проверить гипотезу о равенстве групповых средних.
Указание: проверить решение задачи с помощью программы «Statistica 10».
5. Двум группам белых мышей, по 10 животных в каждой, вводились биопрепараты. Животным первой группы вводился лизат сердца «N/10», а животным второй группы - экстракт мышц «10N». Через 86 дней животные были забиты и определено отношение веса сердца к общему весу каждого в %. Все выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями. Результаты испытаний занесены в таблицу.
| Номер испытания i | Уровень фактора «F» | ||
| F1 (лизат сердца) N/10 | F2 (экстракт мышц) 10N | F3 (контроль) | |
| 1 | 0,46 | 0,47 | 0,55 |
| 2 | 0,48 | 0,46 | 0,58 |
| 3 | 0,45 | 0,48 | 0,60 |
| 4 | 0,49 | 0,50 | 0,62 |
| 5 | 0,47 | 0,51 | 0,61 |
| 6 | 0,50 | 0,48 | 0,57 |
| 7 | 0,44 | 0,52 | 0,60 |
| 8 | 0,48 | 0,45 | 0,59 |
| 9 | 0,46 | 0,50 | 0,58 |
| 10 | 0,43 | 0,49 | 0,56 |
При уровне значимости 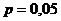 , методом дисперсионного анализа требуется проверить гипотезу о равенстве групповых средних.
, методом дисперсионного анализа требуется проверить гипотезу о равенстве групповых средних.
Указание: проверить решение задачи с помощью программы «Statistica 10».
6. Имеются данные о количестве сцеженного и высосанного молока у 8 кормящих матерей, страдающих гиполактией, в течение 6 суточных кормлений. Проверить имеется ли различие между количеством сцеженного и высосанного молока во время шести кормлений в течение суток. Данные приведены в таблице.
| Час кормления | Кормящие матери | ||||||||
| 1-я | 2-я | 3-я | 4-я | 5-я | 6-я | 7-я | 8-я | 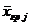
| |
| 6 | 100 | - | - | 126 | 133 | 101 | - | 128 | 117,6 |
| 9 | - | 119 | 122 | 104 | 115 | 102 | 128 | - | 115 |
| 12 | 101 | 87 | 88 | 105 | 93 | 102 | 74 | 94 | 93 |
| 15 | - | 83 | - | 87 | 96 | - | - | 97 | 90,75 |
| 18 | - | 84 | 83 | 96 | 83 | 90 | 101 | 64 | 85,86 |
| 21 | 69 | 86 | 80 | 82 | 80 | 99 | 81 | 71 | 81 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
7. В течение нескольких дней подопытные животные подвергались радиоактивному облучению. Можно ли говорить об изменении радиоактивности крови в связи с длительностью облучения в разных группах животных? Результаты приведены в таблице.
| День облучения | Радиоактивность в условных единицах | |||
| 1-я группа | 2-я группа | 3-я группа | 4-я группа | |
| 1-й | 30 | 28 | 26 | 24 |
| 1-й | 28 | 30 | 27 | 26 |
| 1-й | 34 | 32 | 30 | 28 |
| 1-й | 42 | 40 | 38 | 34 |
| 2-й | 36 | 38 | 34 | 32 |
| 2-й | 28 | 30 | 29 | 26 |
| 2-й | 34 | 32 | 30 | 28 |
| 2-й | 36 | 30 | 32 | 26 |
| 3-й | 40 | 38 | 36 | 24 |
| 3-й | 38 | 36 | 34 | 32 |
| 3-й | 34 | 45 | 40 | 38 |
| 3-й | 37 | 38 | 40 | 36 |
Указание. Для решения использовать программу «Statistica 10».
8. Исследовалось влияние на вестибуло-вегетативную устойчивость (ВВУ) здоровых мужчин в возрасте 20-30 лет двух факторов: «А» - специальной физической и аутогенной тренировки на трех уровнях; «В» - медикаментозных средств, предупреждающих укачивание, на четырех уровнях.
Уровни фактора «А»:
А1 - систематическая тренировка в течение более 3 месяцев;
А2 - систематическая тренировка в течение 1-3 месяцев;
А3 - несистематическая тренировка.
Уровни фактора «В»:
В1 - алмид;
В2 - амтизол;
В3 - бемитил;
В4 - гутимин.
Испытания проводились с людьми со слабой ВВУ (со временем укачивания на стуле двойного вращения до неприятных ощущений не более 3 мин.). На каждом сочетании уровней наблюдали трех человек. Всего опытов проведено 36. Параметром, характеризующим влияние факторов «А» и «В», являлось время укачивания до появления неприятных ощущений – «Х» (мин). Данные опытов представлены в таблице.
| № | А | В | Х |
| 1 | 1 | 1 | 15 |
| 2 | 1 | 1 | 14 |
| 3 | 1 | 1 | 15 |
| 4 | 1 | 2 | 12 |
| 5 | 1 | 2 | 8 |
| 6 | 1 | 2 | 10 |
| 7 | 1 | 3 | 8 |
| 8 | 1 | 3 | 9 |
| 9 | 1 | 3 | 6 |
| 10 | 1 | 4 | 7 |
| 11 | 1 | 4 | 10 |
| 12 | 1 | 4 | 4 |
| 13 | 2 | 1 | 12 |
| 14 | 2 | 1 | 14 |
| 15 | 2 | 1 | 13 |
| 16 | 2 | 2 | 10 |
| 17 | 2 | 2 | 9 |
| 18 | 2 | 2 | 6 |
| 19 | 2 | 3 | 7 |
| 20 | 2 | 3 | 5 |
| 21 | 2 | 3 | 6 |
| 22 | 2 | 4 | 6 |
| 23 | 2 | 4 | 3 |
| 24 | 2 | 4 | 5 |
| 25 | 3 | 1 | 12 |
| 26 | 3 | 1 | 8 |
| 27 | 3 | 1 | 6 |
| 28 | 3 | 2 | 5 |
| 29 | 3 | 2 | 7 |
| 30 | 3 | 2 | 4 |
| 31 | 3 | 3 | 5 |
| 32 | 3 | 3 | 4 |
| 33 | 3 | 3 | 3 |
| 34 | 3 | 4 | 4 |
| 35 | 3 | 4 | 3 |
| 36 | 3 | 4 | 4 |
Провести двухфакторный дисперсионный анализ параметра «Х» и сделать выводы. Построить графики средних значений параметра «Х» на различных уровнях факторов «А» и «В».
Указание. Для решения использовать программу «Statistica 10».
9. Исследовалась длительность лечения 27 пациентов с механической травмой в городских клиниках. Показателем длительности лечения взят срок стационарного лечения в днях - SROKL.
Качественные факторы, влияющие на длительность лечения:
· тяжесть состояния больного при поступлении в клинику - TIAJ, на трех уровнях:
1 - легкая,
2 - средняя,
3 - тяжелая;
· локализация травмы - MIKST, на трех уровнях:
1 - травма конечностей,
2 - травма груди и живота,
3 - сочетанная травма.
На каждом из 9 сочетании уровней наблюдалось по три человека. Данные наблюдений представлены в таблице.
| № | TIAJ | MIKST | SROKL |
| 1 | 2 | 1 | 58 |
| 2 | 1 | 2 | 43 |
| 3 | 2 | 3 | 110 |
| 4 | 1 | 2 | 48 |
| 5 | 3 | 1 | 96 |
| 6 | 1 | 1 | 28 |
| 7 | 1 | 2 | 41 |
| 8 | 2 | 2 | 64 |
| 9 | 2 | 2 | 78 |
| 10 | 2 | 3 | 115 |
| 11 | 1 | 1 | 15 |
| 12 | 2 | 2 | 64 |
| 13 | 1 | 1 | 35 |
| 14 | 2 | 1 | 49 |
| 15 | 1 | 1 | 28 |
| 16 | 3 | 2 | 112 |
| 17 | 2 | 3 | 88 |
| 18 | 2 | 1 | 77 |
| 19 | 1 | 3 | 41 |
| 20 | 1 | 3 | 36 |
| 21 | 3 | 3 | 120 |
| 22 | 3 | 3 | 100 |
| 23 | 2 | 3 | 98 |
| 24 | 1 | 3 | 45 |
| 25 | 2 | 1 | 58 |
| 26 | 3 | 1 | 98 |
| 27 | 3 | 2 | 100 |
Провести двухфакторный дисперсионный анализ и сделать выводы.
Указание. Для решения использовать программу «Statistica 10».
10. Имеются данные о причинах смертности в разных социальных группах населения. С помощью кртерия Крускала-Уоллиса проверить гипотезу об однородности этих групп. Данные приведены в таблице.
| Причина смерти | Вид деятельности | ||||
| Руководители высшего звена | Преподаватели | Руководители среднего звена | Сельхоз. рабочие | Промышленные рабочие | |
| Новообразования | 150 | 140 | 205 | 290 | 350 |
| Сердечно-сосудистые заболевания | 130 | 150 | 180 | 190 | 185 |
| Несчастные случаи | 45 | 30 | 75 | 175 | 95 |
| Цирроз печени | 15 | 16 | 33 | 75 | 95 |
| Самоубийства | 20 | 25 | 36 | 30 | 45 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
11. Имеются данные о смертности населения от болезней системы кровобращения за один год (на 100 тыс. населения). С помощью критерия Краскела-Уоллиса проверить гипотезу об однородности четырех групп (мужчин и женщин городского и сельского населения). Данные приведены в таблице.
| Возрастная группа | Городское население | Сельское население | ||
| Мужчины | Женщины | Мужчины | Женщины | |
| 30-34 | 44,1 | 18,5 | 59,2 | 30,7 |
| 35-39 | 83,9 | 30,1 | 98,1 | 48,2 |
| 40-44 | 156,5 | 55,1 | 153,8 | 65,8 |
| 45-49 | 263,4 | 104,9 | 246,8 | 109,3 |
| 50-54 | 450,8 | 194,3 | 394,8 | 185,9 |
| 55-59 | 750,4 | 338,0 | 617,3 | 293,8 |
| 60-64 | 1296,6 | 666,2 | 1048,4 | 569,6 |
| 65-69 | 2116,5 | 1238,2 | 1697,0 | 1055,0 |
| 70-74 | 3741,5 | 2664,1 | 3169,2 | 2319,2 |
| 75-79 | 6182,9 | 4837,4 | 5044,6 | 4012,1 |
| 80-84 | 10080,7 | 8547,1 | 8680,5 | 7587,0 |
| 85 и старше | 16562,3 | 14682,5 | 14489,4 | 13671,9 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
v Краткая теория
Дисперсионным анализом называют группу статистических методов, разработанных английским математиком и генетиком Р. Фишером в 20-х годах ХХ-го века для ряда экспериментальных задач биологии и сельского хозяйства.
Постановка задачи. Пусть даны генеральные совокупности X1, X2,…, Xk., где:
· все «k» генеральных совокупностей распределены нормально;
· дисперсии всех генеральных совокупностей одинаковы.
При этих условиях и заданном уровне значимости «р» требуется проверить нулевую гипотезу о равенстве выборочных средних, т.е. H0: 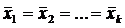 .
.
Каждая из генеральных совокупностей подвержена влиянию одного или нескольких факторов, которые могут изменять их средние значения.
Фактором называется показатель, который оказывает влияние на конечный результат.
Конкретную реализацию фактора называют уровнем фактора.
Значение измеряемого признака называют откликом на фактор.
В зависимости от количества изучаемых факторов дисперсионный анализ делится на однофакторный и многофакторный.
Выборочные данные для однофакторного дисперсионного анализа оформляют в виде таблицы (таблица 8.1).
Таблица 8.1.
| Номер испытания | Уровень фактора «А» | |||
| A1 | A2 | … | Ak | |
| 1 | x11 | x12 | … | x1k |
| 2 | x21 | x22 | … | x2k |
| ... | … | … | … | … |
| r | 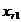
| 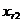
| … | 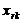
|
| Групповая средняя | 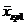
| 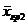
| … | 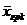
|
Основная цель дисперсионного анализа состоит в разбиении выборочной дисперсии на две компоненты:
- первая – это факторная дисперсия, она соответствует влиянию фактора на изменчивость средних значений;
- вторая – это остаточная дисперсия, она обусловлена случайными причинами и не влияет на изменчивость средних значений.
Для численной оценки влияния исследуемого фактора используют сравнение этих компонент с помощью F-критерия Фишера.
Факторная дисперсия ( 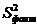 или
или 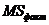 ) – это дисперсия, которая соответствует влиянию фактора на изменение средних значений выборки:
) – это дисперсия, которая соответствует влиянию фактора на изменение средних значений выборки:
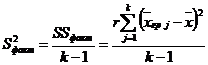 , (8.1)
, (8.1)
где 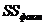 - факторная сумма квадратов отклонений, k - количество уровней фактора, r -количество значений в каждой группе,
- факторная сумма квадратов отклонений, k - количество уровней фактора, r -количество значений в каждой группе, 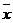 - общая средняя,
- общая средняя, 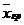 - групповая средняя.
- групповая средняя.
Остаточная дисперсия ( 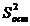 или
или 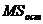 ) – это дисперсия, возникающая по случайными причинами и не влияющая на изменение средних значений выборки:
) – это дисперсия, возникающая по случайными причинами и не влияющая на изменение средних значений выборки:
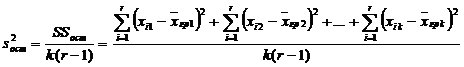 , (8.2)
, (8.2)
где 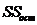 - остаточная сумма квадратов отклонений.
- остаточная сумма квадратов отклонений.
Общая дисперсия ( 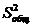 или
или 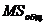 ) – это сумма факторной и остаточной дисперсий:
) – это сумма факторной и остаточной дисперсий:
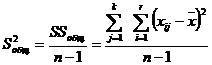 , (8.3)
, (8.3)
где 
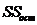 .
.
Схема применения однофакторного дисперсионного анализа:
a. Н0: 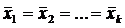 .
.
H1: 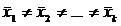 .
.
b. р=0,05- уровень значимости.
c. 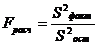 . (8.4)
. (8.4)
d. 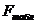 (р, f1, f2), [см. Приложение 4],
(р, f1, f2), [см. Приложение 4],
где f1=k-1, f2=k(r-1) – число степеней свободы, k - количество уровней фактора, r - количество значений в каждой группе.
e. Если 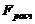 ≤
≤ 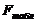 , то «H0» принимается.
, то «H0» принимается.
Если 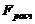 >
> 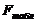 , то «H0» отвергается.
, то «H0» отвергается.
H-критерий Крускала – Уоллиса является непараметрическим аналогом однофакторного дисперсионного анализа для сравнения трех и более независимых групп.
Данный критерий рассчитывается с использованием не фактических значений данных, а их рангов.
Н-критерий используется, если распределение в группах не является нормальным.
При сопоставлении трех выборок допускается, чтобы в каждой из них было не менее 3 наблюдений, или в одной из них 4 наблюдения, а в двух других – по 2; при этом неважно, в какой именно выборке сколько испытуемых, а важно соотношение 4:2:2.
Таблица критических значений Н-критерия предусмотрена только для случая, когда число выборок k≤5, а число испытуемых в каждой группе ni≤8. При большом количестве выборок и испытуемых в каждой выборке необходимо пользоваться таблицей критических значений χ2-критерия, т.к. критерий Крускала-Уоллиса асимптотически приближается к распределению «χ2».
Схема применения H-критерия Крускала – Уоллиса:
1) Н0: 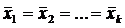 .
.
H1: 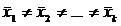 .
.
2) р=0,05- уровень значимости.
3) 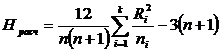 , (8.5)
, (8.5)
где 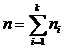 - общее число наблюдений по всем группам,
- общее число наблюдений по всем группам, 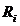 - сумма рангов i-ой выборки.
- сумма рангов i-ой выборки.
4) В случае, когда число выборок k≤5  (р;n1;n2;…;n5) , [см. Приложение 8],
(р;n1;n2;…;n5) , [см. Приложение 8],
где n1, n2, …, n5 – объемы рассматриваемых выборок.
В случае, когда число выборок k>5 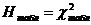 (р; f), [см. Приложение 2],
(р; f), [см. Приложение 2],
где f=k-1 – число степеней свободы.
5) Если 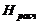 <
< 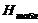 , то «H0» принимается.
, то «H0» принимается.
Если 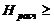
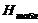 , то «H0» отвергается.
, то «H0» отвергается.
Двухфакторный дисперсионный анализ – система статистических методов исследования действия на признак двух организованных факторов.
Двухфакторный дисперсионный анализ позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие.
Реализация однофакторного дисперсионного анализа в программе «Statistica».
Пример 8.1. Разнообразие роста 7 женщин и 5 мужчин задано в таблице:
| № | Пол | Рост |
| 1 | Мужчина | 186 |
| 2 | Женщина | 169 |
| 3 | Женщина | 166 |
| 4 | Мужчина | 188 |
| 5 | Женщина | 172 |
| 6 | Женщина | 179 |
| 7 | Женщина | 165 |
| 8 | Мужчина | 174 |
| 9 | Женщина | 163 |
| 10 | Мужчина | 162 |
| 11 | Женщина | 162 |
| 12 | Мужчина | 190 |
Провести однофакторный дисперсионный анализ: сравнить, значимо ли отличаются мужчины и женщины в охарактеризованной группе по росту.
1. Создать таблицу данных «Разнообразие роста» размером 2*12 в программе «Statistica» и внести исходные данные (рисунок 8.1).
2. Провести тест на нормальность
Тест данных на нормальность можно провести двумя способами:
1) Statistics→Basic Statistics→Descriptive Statistics→Normality (рисунок 8.1).
Во вкладке «Normality» можно выбрать используемые тесты нормальности распределения.
При нажатии на кнопку «Frequency tables» появится частотная таблица, а на кнопку «Histograms» — гистограмма. На таблице и гистограмме будут приведены результаты различных тестов.
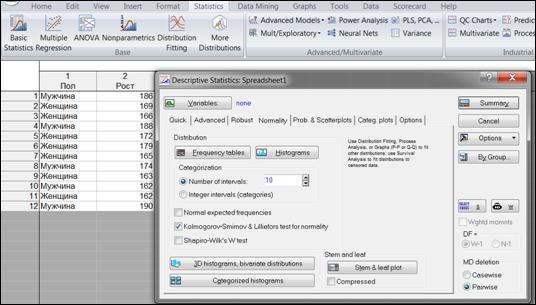
Рисунок 8.1. Окно «Descriptive Statistics», вкладка «Normality»
2) В диалоге построения гистограмм (Graphs/Histograms...) выбрать вкладку «Advanced» (рисунок 8.2).
В ее нижней части есть блок «Statistics». Отметить на ней «Shapiro-Wilk test» и «Kolmogorov-Smirnov test», как это показано на рисунке 8.2.
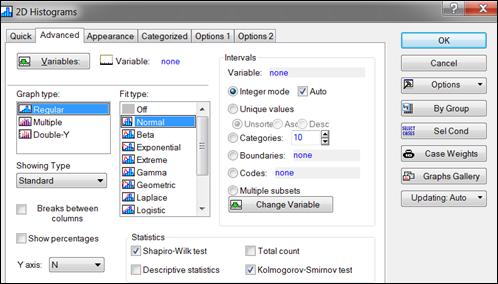
Рисунок 8.2. Статистические тесты на нормальность распределения в диалоге построения гистограмм
На экране появится гистограмма (рисунок 8.3). На гистограмме наблюдается отличие распределения роста в выборке от нормального (в середине — «провал»).
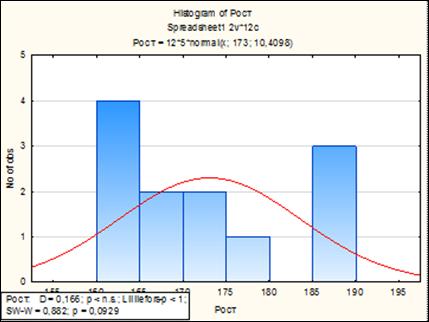
Рисунок 8.3. Гистограмма, построенная с параметрами,
указанными на предыдущем рисунке
Третья строка в заголовке графика указывает параметры нормального распределения, к которому оказалось ближе всего наблюдаемое распределение. Генеральное среднее составляет 173, генеральное стандартное отклонение — 10,4. Внизу на графике указаны результаты тестов на нормальность. D — это критерий Колмогорова-Смирнова, а SW-W — Шапиро-Вилка.
Как видно, для всех использованных тестов отличия распределения по росту от нормального распределения оказались незначимыми (во всех случаях р>0,05).
Дисперсионный анализ относительно устойчив к отклонениям от нормальности, поэтому применяется в статистике.
3. Провести однофакторный дисперсионный анализ.
В таблице исходных данных выбрать Statistics →ANOVA→ в окне «Type of analysis» выбрать вариант «One-way ANOVA» (Однофакторный дисперсионный анализ), а в окне «Specification method» – вариант «Quick specs dialog» (рисунок 8.4) и нажать кнопку «OK».
В открывшемся окне в поле «Variables» (Переменные) указать: «Dependent» (Зависимые переменные) столбец «Рост», «Categorical factor» (Категориальный фактор) столбец «Пол» (рисунок 8.5).
В данном варианте анализа рассматривается только один фактор.
Рисунок 8.4. Окно «General ANOVA / MANOVA» (Дисперсионный анализ)
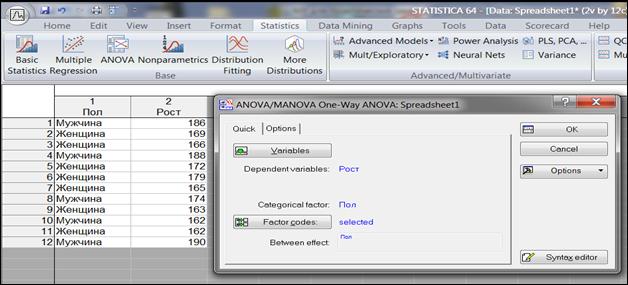
Рисунок 8.5. Окно «One-Way ANОVA» (Однофакторный дисперсионный анализ)
В окне «Factor codes» (Коды факторов) указать те значения рассматриваемого фактора, которые нужно обрабатывать в ходе данного анализа.
Все имеющиеся значения можно посмотреть с помощью кнопки «Zoom». Если нужно рассматривать все значения фактора, то нужно нажать кнопку «All» (Все).
Затем нажать кнопку «OK», перейти в окно «ANOVA Results 1» и выбрать вкладку «Quick» (Быстрый) (рисунок 8.6).
Рисунок 8.6. Вкладка «Quick» окна результатов дисперсионного анализа
Кнопка «All effects/Graphs» (Все эффекты/Графики) позволяет увидеть, как соотносятся средние двух групп.
Над графиком указывается число степеней свободы, значения «F»и «p» для рассматриваемого фактора (рисунок 8.7).
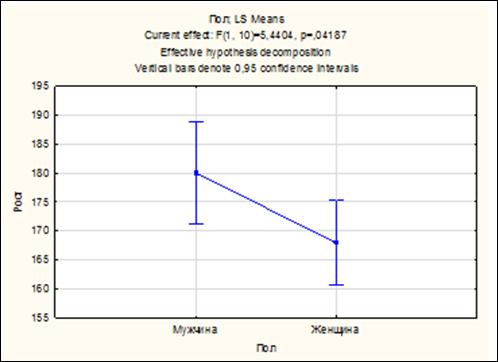
Рисунок 8.7. Графическое отображение результатов дисперсионного анализа
Кнопка «All effects» (Все эффекты) позволяет получить таблицу дисперсионного анализа (рисунок 8.8).
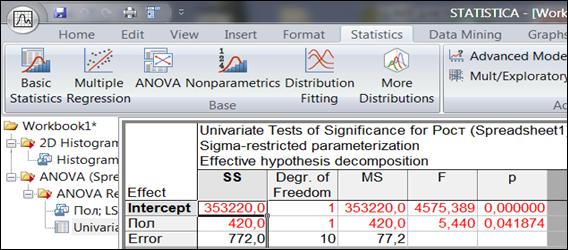
Рисунок 8.8. Таблица с результатами дисперсионного анализа
В третьей строке таблицы указана сумма квадратов, количество степеней свободы и средние квадраты для ошибки (внутригрупповой изменчивости).
Во второй строке таблицы указаны аналогичные показатели для исследуемого фактора (Пол), значение критерия «F», и уровень его значимости.
То, что действие рассматриваемого фактора оказалось значимым, показывает выделение красным цветом.
В первой строке приведены данные по показателю «Intercept», данные этой строки можно проигнорировать.
Реализация двухфакторного дисперсионного анализа в программе «Statistica».
Пример 8.2. Имеются данные с результатами тестирования студентов мужского и женского пола по трем тестам: «легкому», «среднему» и «сложному». Данные расположены не случайно, а сгруппированы по полу, по сложности теста, а внутри этих групп–по возрастанию полученного балла:
| № | Пол | Тест | Балл |
| 1 | Женщина | Легкий | 64 |
| 2 | Женщина | Легкий | 69 |
| 3 | Женщина | Легкий | 73 |
| 4 | Женщина | Легкий | 90 |
| 5 | Женщина | Легкий | 94 |
| 6 | Женщина | Средний | 30 |
| 7 | Женщина | Средний | 39 |
| 8 | Женщина | Средний | 63 |
| 9 | Женщина | Средний | 72 |
| 10 | Женщина | Средний | 76 |
| 11 | Женщина | Сложный | 10 |
| 12 | Женщина | Сложный | 25 |
| 13 | Женщина | Сложный | 34 |
| 14 | Женщина | Сложный | 41 |
| 15 | Женщина | Сложный | 60 |
| 16 | Мужчина | Легкий | 41 |
| 17 | Мужчина | Легкий | 43 |
| 18 | Мужчина | Легкий | 53 |
| 19 | Мужчина | Легкий | 65 |
| 20 | Мужчина | Легкий | 78 |
| 21 | Мужчина | Средний | 43 |
| 22 | Мужчина | Средний | 45 |
| 23 | Мужчина | Средний | 65 |
| 24 | Мужчина | Средний | 71 |
| 25 | Мужчина | Средний | 96 |
| 26 | Мужчина | Сложный | 34 |
| 27 | Мужчина | Сложный | 41 |
| 28 | Мужчина | Сложный | 60 |
| 29 | Мужчина | Сложный | 64 |
| 30 | Мужчина | Сложный | 71 |
Провести двухфакторный дисперсионный анализ: выяснить влияет ли пол человека на результаты тестов.
1. Создать таблицу данных «Результаты тестирования» размером 3*30 в программе «Statistica» и внести исходные данные (рисунок 8.9).
2. Провести двухфакторный дисперсионный анализ.
Statistics→ANOVA→выбрать в окне «Type of analysis» вариант «Factorial ANOVA» (Многофакторный дисперсионный анализ), а в окне «Specification method» – вариант «Quick specs dialog» (рисунок 8.9) и нажать кнопку «OK».
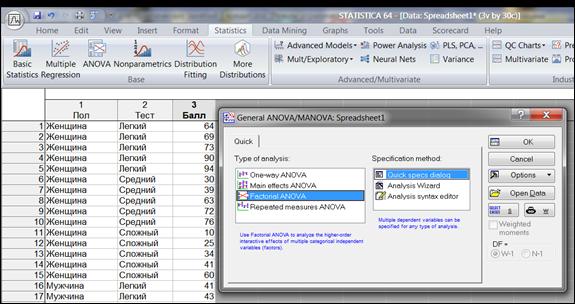
Рисунок 8.9. Стартовое окно для проведения многофакторного анализа
В открывшемся окне в поле «Variables» указать в окне «Dependent variables list» столбец «Балл», а в окне «Categorical predictors (factor)» - столбцы - «Пол» и «Тест», нажать кнопку «OK».
В диалоговом окне «Factor codes» для обоих факторов выбрать кнопку «All» (рисунок 8.10).
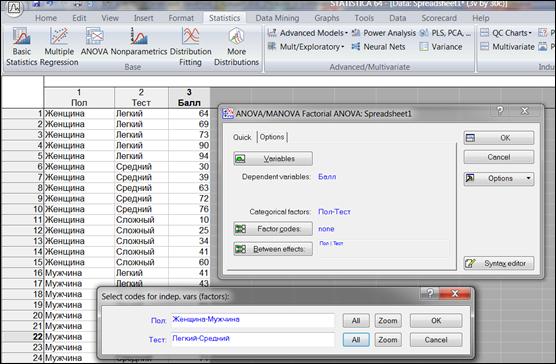
Рисунок 8.10. Выбор кодов факторов. В обоих случаях нажаты кнопки «All»
На экране появляется окно «ANOVA Results 1».
Кнопка «All effects» выводит таблицу дисперсионного анализа (рисунок 8.11).
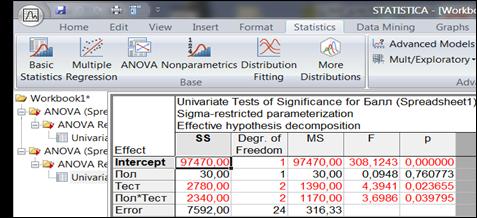
Рисунок 8.11. Основная таблица результатов двухфакторного анализа
Как видно из таблицы, влияние признака «Пол» незначимо, но и влияние признака «Тест», и взаимодействие «Пол*Тест» оказывается значимым.
Чтобы понять, в чем заключается такое взаимодействие, нужно построить график с помощью кнопки «All effects/Graphs» в окне «ANOVA Results 1». В открывающемся диалоговом окне выбрать строку «Пол*Тест».
Программа предлагает два варианта построения графика: с отображением на оси абсцисс признака «Тест» или признака «Пол».
Рассмотрим оба варианта (рисунок 8.12 и рисунок 8.13).
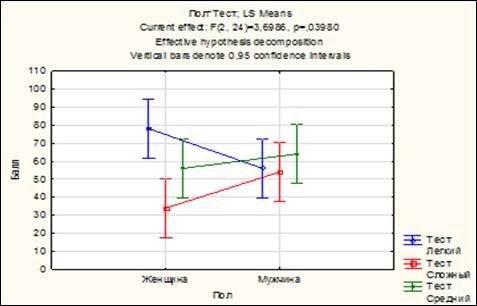
Рисунок 8.12. Вариант графика, отражающего взаимодействие факторов, в котором на оси абсцисс показан признак «Пол», а точки, соответствующие определенным значениям признака «Тест», показаны линиями
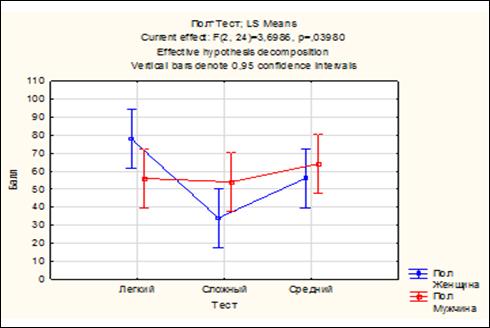
Рисунок 8.13 Вариант графика, отражающего взаимодействие факторов, в котором на оси абсцисс показан признак «Тест», а точки, соответствующие определенным значениям признака «Пол», показаны линиями
Второй график более наглядный. На нем линиями показаны результаты испытуемых двух полов.
Реакция женщин: хорошо решают легкие тесты, при решении средних тестов они получают плохие результаты, а в случае сложных тестов их результаты опять повышаются.
Реакция мужчин: легкие тесты решают хорошо, на тестах средней сложности результат практически такой же, а сложные тесты они решают лучше всего.
Вывод: пол человека не влияет на результаты тестов.
Реализация критерия Крускала-Уоллиса в программе «Statistica».
Пример 8.3. Для оценки дозовой нагрузки химическими веществами, загрязняющими питьевую воду, изучалось количество потребляемой для питья водопроводной воды среди разных возрастных групп населения. В результате получены следующие данные:
| Дети (n1=8) | Подростки (n2=7) | Взрослые (n3=9) |
| Вода, л/день | Вода, л/день | Вода, л/день |
| 1,22 | 1,47 | 1,56 |
| 1,24 | 1,52 | 1,58 |
| 1,31 | 1,55 | 1,81 |
| 1,31 | 1,70 | 1,89 |
| 1,45 | 1,93 | 2,00 |
| 1,52 | 2,00 | 2,00 |
| 1,84 | 3,00 | 2,55 |
| 2,52 | 2,58 | |
| 4,00 | ||
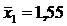
| 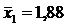
| 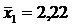
|
Проверить гипотезу о равенстве средних значений количества потребляемой для питья воды в популяциях детей, подростков и взрослого.
1. Создать таблицу данных «Потребление воды» размером 2*24 в программе «Statistica» и внести исходные данные (рисунок 8.14).
2. Проверить гипотезу об однородности выборок с помощью критерия Крускала-Уоллиса.
Выбрать Statistics→Nonparametrics→Comparing multiple indep. samples (groups) (Сравнение многих независимых выборок (групп)) (рисунок 8.15) и нажать кнопку «OK».
Рисунок 8.15. Выбор процедуры «Comparing multiple indep. samples (groups)»
В диалоговом окне, нажать кнопку «Variables», указать в правой части окна группирующий признак (столбец, содержащий коды групп), а в левой части окна – столбец, содержащий анализируемый признак (рисунок 8.16) и нажать кнопку «OK».
Рисунок 8.16. Задание переменных
В диалоговом окне нажать кнопку «Summary: Kruskal-Wallis ANOVA & Median test».
На экране появится итоговая таблица (рисунок 8.17).
Рисунок 8.17. Итоговая таблица с результатами сравнения трех независимых выборок по критерию Крускала-Уоллиса
В заголовке таблицы указано расчетное значение статистики критерия Нрасч.=8,265123 и значение р=0,0160.
Если р > 0,05, то нулевая гипотеза принимается.
Если р < 0,05, то нулевая гипотеза отвергается.
В данном примере р=0,160, значит гипотеза о равенстве средних отвергается, т.е. в разных возрастных группах ежедневно потребляется разное количество питьевой воды.
Для нагладности можно построить график «ящик с усами», нажав в окне анализа кнопку «Box & whisker plots for all variables» (рисунок 8.18).
Рисунок 8.18. График «ящик с усами».
6. Литература:
1. Боровиков В.П. Популярное введение в программу STATISTICA. - М.: Компьютер Пресс, 1998. - 240 с.
2. Боровиков В.П. STATISTICA. Искусство анализа данных на компьютере: для профессионалов / В. Боровиков. - СПб.: Питер, 2004. - 688 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов.- 9-е изд., стер. - М.: Высш. шк., 2003. - 479 с.
4. Лобоцкая Н.Л. Высшая математика. / Н.Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. - Мн.: Высшая школа, 1987. - 319 с.
5. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах/ Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
6. Реброва О.Ю. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA. - М.: МедиаСфера, 2002.-312с.
7. Халафян А.А. Statistica 6. Статистический анализ данных. 3-е изд. Учебник - М.: ООО «Бином-Пресс», 2007. - 512 с.
8. http://matstats.ru/
9. http://www.statsoft.ru/
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №9
1. Тема: Корреляционный анализ. Выборочный коэффициент корреляции Пирсона. Сила и характер связи между параметрами. Ранговая корреляция. Коэффициент ранговой корреляции Спирмена.
2. Цель: Изучение основ корреляционно анализа.
3. Задачи обучения: Сформировать навыки проведения корреляционного анализа.
4. Основные вопросы темы:
1. Что представляет собой корреляционная зависимость?
2. Как вычисляется линейный коэффициент корреляции?
3. Какие виды корреляционной зависимости Вы знаете?
4. Как определяется достоверность коэффициента корреляции?
5. В каких случаях для оценки зависимости применяют ранговую корреляцию?
6. Что такое ранжирование?
7. Как рассчитывается коэффициент ранговой корреляции Спирмена?
5. Методы обучения и преподавания: письменное решение задач
v Задания:
1. Ознакомиться с краткой теорией практического занятия №9.
2. Ответить на основные вопросы темы.
3. Провести корреляционный анализ с целью изучения зависимости заболеваемости инфарктом миокарда по месяцам года от среднемесячной температуры воздуха. Исходные данные представлены в таблице.
| Месяц | Заболеваемость инфарктом миокарда по месяцам (на 10 000 тыс. жителей) | Среднемесячная температура воздуха |
| Январь | 1,6 | -7,1 |
| Февраль | 1,23 | -7,7 |
| Март | 1,14 | -5,8 |
| Апрель | 1,13 | -4,1 |
| Май | 1,12 | +13 |
| Июнь | 1,02 | +14,9 |
| Июль | 0,91 | +18,8 |
| Август | 0,82 | +15,6 |
| Сентябрь | 1,06 | +9,0 |
| Октябрь | 1,22 | +6,0 |
| Ноябрь | 1,33 | -1,0 |
| Декабрь | 1,4 | -7,7 |
4. Провести корреляционный анализ с целью изучения зависимости между систолическим артериальным давлением (САД) и весом женщин в возрасте от 20 до 30 лет. Исходные данные представлены в таблице.
| САД, у | 110 | 125 | 80 | 120 | 115 | 140 | 120 | 110 | 85 |
| Вес, (кг) х | 53 | 60 | 58 | 55 | 68 | 70 | 64 | 55 | 55 |
5. Было проведено изучение зависимости между длительностью курения и числом заболеваний. Вычислить коэффициент корреляции Спирмена. Исходные данные представлены в таблице.
| Стаж курения, лет | Число заболеваний |
| 2 | 5 |
| 4 | 6 |
| 5 | 4 |
| 1 | 1 |
| 3 | 2 |
| 2 | 5 |
| 4 | 4 |
| 5 | 6 |
| 7 | 5 |
6. Было проведено изучение зависимости между толщиной кожного рубца и временем его замораживания в целях криодеструкции. Вычислить коэффициент корреляции Спирмена. Исходные данные представлены в таблице.
| Толщина кожного рубца, мм | Время замораживания, мин. |
| 3 | 0,6 |
| 5 | 1 |
| 8 | 1,6 |
| 9 | 1,5 |
| 12 | 1,7 |
| 14 | 1,6 |
| 17 | 2,4 |
| 20 | 3 |
v Краткая теория
Корелляционный анализ - это количественный метод определения тесноты и направления связи между двумя и более случайными величинами.
Для того чтобы охарактеризовать связь между переменными численно, вводится понятие коэффициента корреляции.
Коэффициент корреляции - показатель, характеризующий силу связи и ее направление, принимает значения в промежутке [-1, 1].
Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока (таблица 9.1).
Таблица 9.1.
| Количественная мера тесноты связи | Качественная характеристика силы связи |
| 0,1 - 0,3 | Слабая |
| 0,3 - 0,5 | Умеренная |
| 0,5 - 0,7 | Заметная |
| 0,7 - 0,9 | Высокая |
| 0,9 - 1 | Сильная |
По направлению различают прямую и обратную корреляционную связь.
Прямая корреляционная связь - связь, при которой увеличение одной переменной связано с увеличением другой переменной.
Обратная корреляционная связь - связь, при которой увеличение одной переменной связано с уменьшением другой переменной.
При прямой связи коэффициент корреляции принимает значения от «0» до «+1».
При обратной связи коэффициент корреляции принимает значения от «-1» до «0».
Если коэффициент корреляции равен «0», то связь между явлениями отсутствует.
Если коэффициент корреляции равен «+1» или «–1», то связь между явлениями функциональная.
Линейный (парный) коэффициент корреляции Пирсона-показатель, характеризующий силу связи и ее направление:
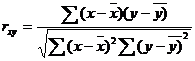 , (9.1)
, (9.1)
где rxy – коэффициент корреляции; х и у – коррелируемые ряды; 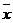 ,
, 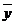 - средние значения.
- средние значения.
Парный коэффициент корреляции является параметрическим коэффициентом.
Применение парного коэффициента корреляции возможно, если выполняются следующие условия:
1) сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений;
2) распределения переменных должны быть близки к нормальному;
3) число значений рассматриваемых переменных должно быть одинаковым.
Достоверность коэффициента корреляции определяется сравнением его с вычисляемой средней ошибкой. Средняя ошибка коэффициента корреляции равна
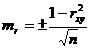 , (9.2)
, (9.2)
где rxy – коэффициент корреляции; n - число наблюдений.
Коэффициент корреляции считается достоверным, если не менее чем в 3 раза превышает свою среднюю ошибку. Иначе необходимо увеличить число наблюдений и вновь вычислить коэффициент и его ошибку.
Достоверность коэффициента корреляции определяется также по специальным таблицам.
При анализе клинических и фармацевтических явлений часто пользуются непараметрическими коэффициентами связи, например, ранговым коэффициентом Спирмена.
Коэффициент ранговой корреляции Спирмена используется для определения тесноты связей как между количественными, так и между качественными признаками при условии, если их значения упорядочить или проранжировать по степени убывания или возрастания признака.
Коэффициент ранговой корреляции Спирмена:
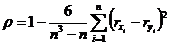 , (9.3)
, (9.3)
где n - объем совокупности, 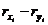 - разность между рангами i-го объекта.
- разность между рангами i-го объекта.
Качественную характеристику тесноты связи коэффициента ранговой корреляции, как и других коэффициентов корреляции, можно оценить по шкале Чеддока.
Коэффициент ранговой корреляции Спирмена применяется в случае, если объем выборки n удовлетворяет неравенству 5≤n≤40.
6. Литература:
6. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов / В.Е. Гмурман. - М.: Высшая школа, 2003. - 479 с.
7. Койчубеков Б.К. Биостатистика: Учебное пособие. - Алматы: Эверо, 2014. - 154 с.
8. Лобоцкая Н.Л. Высшая математика. / Н.Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. - Мн.: Высшая школа, 1987. - 319 с.
9. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах / Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
10. Основы высшей математики и математической статистики: Учебник / И.В. Павлушков и соавт. - М.: ГЭОТАР-МЕД, 2004. - 424 с.
11. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие / ред. Кучеренко В.З. - 4-е изд., перераб. и доп. – М.: ГЭОТАР - Медиа, 2011. - 256 с.
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №10
1. Тема: Регрессионный анализ. Линейная регрессия. Нахождение линейного уравнения парной регрессии. Оценка достоверности показателей регрессии. Коэффициент детерминации. Корреляционно-регрессионный анализ в программе «Statistica».
2. Цель: Изучение основ регрессионного анализа, реализация корреляционно-регрессионного анализа в программе «Statistica».
3. Задачи обучения: Сформировать навыки проведения регрессионного анализа и реализации корреляционно-регрессионного анализа в программе «Statistica».
4. Основные вопросы темы:
1. В чем заключается суть регрессионного анализа?
2. Что такое регрессия и каких видов она бывает?
3. Какие виды уравнений парной регрессии Вы знаете?
4. В чем заключается суть метода наименьших квадратов?
5. По каким формулам определяются коэффициенты парной линейной регрессии?
6. В каком модуле программы «Statistica»производится вычисление коэффициента ранговой корреляции Спирмена?
7. В каком модуле программы «Statistica»осуществляется корреляционно-регрессионный анализ?
8. Какая информация содержится в итоговой таблице результатов корреляционно-регрессионного анализа в «Statistica»?
6. Методы обучения и преподавания: письменное решение задач, статистическая обработка материалов с помощью компьютерной программы «Statistica 10».
v Задания:
1. Ознакомиться с краткой теорией практического занятия №10.
2. Ответить на основные вопросы темы.
3. Выполнить примеры 10.1, 10.2.
4. Провести регрессионный анализ с целью изучения зависимости заболеваемости инфарктом миокарда по месяцам года от среднемесячной температуры воздуха. Исходные данные представлены в таблице.
| Месяц | Заболеваемость инфарктом миокарда по месяцам (на 10 000 тыс. жителей) | Среднемесячная температура воздуха |
| Январь | 1,6 | -7,1 |
| Февраль | 1,23 | -7,7 |
| Март | 1,14 | -5,8 |
| Апрель | 1,13 | -4,1 |
| Май | 1,12 | +13 |
| Июнь | 1,02 | +14,9 |
| Июль | 0,91 | +18,8 |
| Август | 0,82 | +15,6 |
| Сентябрь | 1,06 | +9,0 |
| Октябрь | 1,22 | +6,0 |
| Ноябрь | 1,33 | -1,0 |
| Декабрь | 1,4 | -7,7 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
5. Провести регрессионный анализ с целью изучения зависимости между систолическим артериальным давлением (САД) и весом женщин в возрасте от 20 до 30 лет. Исходные данные представлены в таблице.
| САД, у | 110 | 125 | 80 | 120 | 115 | 140 | 120 | 110 | 85 |
| Вес, (кг) х | 53 | 60 | 58 | 55 | 68 | 70 | 64 | 55 | 55 |
Указание: проверить решение задачи с помощью программы «Statistica 10».
6. Было проведено изучение зависимости между длительностью курения и числом заболеваний. Вычислить коэффициент корреляции Спирмена. Исходные данные представлены в таблице.
| Стаж курения, лет | Число заболеваний |
| 2 | 5 |
| 4 | 6 |
| 5 | 4 |
| 1 | 1 |
| 3 | 2 |
| 2 | 5 |
| 4 | 4 |
| 5 | 6 |
| 7 | 5 |
Указание: для решения использовать программу «Statistica 10».
7. Было проведено изучение зависимости между толщиной кожного рубца и временем его замораживания в целях криодеструкции. Вычислить коэффициент корреляции Спирмена. Исходные данные представлены в таблице.
| Толщина кожного рубца, мм | Время замораживания, мин. |
| 3 | 0,6 |
| 5 | 1 |
| 8 | 1,6 |
| 9 | 1,5 |
| 12 | 1,7 |
| 14 | 1,6 |
| 17 | 2,4 |
| 20 | 3 |
Указание: для решения использовать программу «Statistica 10».
v Краткая теория
Регрессионный анализ- метод статистической обработки данных, позволяющий измерить связь между одной или несколькими причинами (факторными признаками) и следствием (результативным признаком).
Признак- это основная отличительная черта, особенность изучаемого явления или процесса.
Результативный признак - исследуемый показатель.
Факторный признак - показатель, влияющий на значение результативного признака.
Целью регрессионного анализа является оценка функциональной зависимости среднего значения результативного признака (у) от факторных (х1, х2, …, хn), которая выражается уравнением регрессии:
у = f (x1, х2, …, хn). (10.1)
Различают два вида регрессии: парную и множественную.
Парная (простая) регрессия:
у = f (x). (10.2)
Результативный признак при парной регрессии рассматривается как функция от одного аргумента, т.е. одного факторного признака.
Множественная регрессия:
у = f (x1, х2, …, хn). (10.3)
Результативный признак рассматривается как функция от нескольких аргументов, т.е. много факторных признаков.
Рассмотрим парную регрессию.
Регрессионный анализ состоит из следующих этапов:
1) определение типа функции;
2) определение коэффициентов регрессии;
3) расчет теоретических значений результативного признака;
4) проверку статистической значимости коэффициентов регрессии;
5) проверку статистической значимости уравнения регрессии.
По направлению связи регрессия делится на:
· прямую регрессию, возникающую при условии, что с увеличением или уменьшением независимой величины «х» значения зависимой величины «у» также соответственно увеличиваются или уменьшаются;
· обратную регрессию, появляющуюся при условии, что с увеличением или уменьшением независимой величины «х» зависимая величина «у» соответственно уменьшается или увеличивается.
Для характеристики связей используют следующие виды уравнений парной регрессии:
· у=a+bx – линейное;
· y=eax+b – экспоненциальное;
· y=a+b/x – гиперболическое;
· y=a+b1x+b2x2 – параболическое;
· y=abx – показательное и др.
где a, b1, b2 - коэффициенты (параметры) уравнения; у - результативный признак; х - факторный признак.
Построение уравнения регрессии сводится к оценке его коэффициентов (параметров), для этого используют метод наименьших квадратов.
Этот метод позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических ух минимальна, то есть
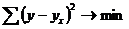 . (10.4)
. (10.4)
Формулы оценки параметров уравнения регрессии у=a+bх по методу наименьших квадратов:
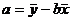 ,
, 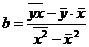 , (10.5)
, (10.5)
где а – свободный коэффициент, b - коэффициент регрессии, показывает на сколько изменится результативный признак «y» при изменении факторного признака «x» на единицу измерения.
Для оценки статистической значимости коэффициентов регрессии используется  -критерий Стьюдента.
-критерий Стьюдента.
Схема проверки значимости коэффициентов регрессии:
6) Н0: a=0, b=0 - коэффициенты регрессии незначимо отличаются от нуля.
Н1: a≠0, b≠0 - коэффициенты регрессии значимо отличаются от нуля.
7) р=0,05.
8) 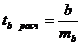 ,
, 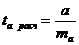 , (10.6)
, (10.6)
где mb, ma - случайные ошибки:
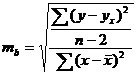 ;
; 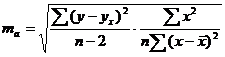 . (10.7)
. (10.7)
9) tтабл(р; f), [см. Приложение 5],
где f=n-k-1 - число степеней свободы (табличное значение), n - число наблюдений, k - число параметров в уравнении при переменных «х».
10) Если 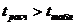 , то
, то 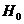 отклоняется, т.е. коэффициент статистически значим.
отклоняется, т.е. коэффициент статистически значим.
Если 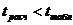 , то
, то 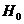 принимается, т.е. коэффициент статистически незначим.
принимается, т.е. коэффициент статистически незначим.
Для проверки значимости построенного уравнения регрессии применяется критерий Фишера.
Схема проверки значимости уравнения регрессии:
1) Н0: уравнение регрессии статистически незначимо.
Н1: уравнение регрессии статистически значимо.
2) р=0,05.
3) 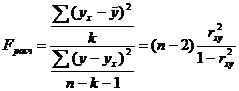 , (10.8)
, (10.8)
где 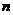 - число наблюдений; k - число параметров в уравнении при переменных «х»; у - фактическое значение результативного признака; yx - теоретическое значение результативного признака;
- число наблюдений; k - число параметров в уравнении при переменных «х»; у - фактическое значение результативного признака; yx - теоретическое значение результативного признака; 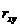 - коэффициент парной кореляции.
- коэффициент парной кореляции.
4) Fтабл(р; f1; f2), [см. Приложение 4],
где f1=k, f2=n-k-1- число степеней свободы (табличные значения).
5) Если Fрасч. > Fтабл, то уравнение регрессии подобрано верно и может применяться на практике.
Если Fрасч < Fтабл, то уравнение регрессии подобрано неверно.
Основным показателем, отражающим меру качества регрессионной модели, является коэффициент детерминации (R2).
Коэффициент детерминации показывает, какая доля вариации зависимой переменной «у» учтена в модели и обусловлена влиянием на нее факторов, включенных в модель.
Коэффициент детерминации (R2) принимает значения в промежутке [0, 1]. Чем ближе R2 к 1, тем выше качество построенного уравнения регрессии. Уравнение регрессии является качественным, если R2 ≥0,8.
Коэффициент детерминации равен квадрату коэффициента корреляции, т.е.
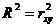 . (10.9)
. (10.9)
Реализация корреляционно-регрессионного анализа в программе «Statistica».
Пример 10.1. В одном населенном пункте зарегистрировано наличие хронической эпидемии дизентерии Флекснера. Предварительный анализ и лабораторные исследования показали, что в питьевой воде водопроводной сети наблюдаются частые «проскоки» нестандартных проб по бактериологическим показателям (фактор риска).Провести корреляционно-регрессионный анализ. Исходные данные представлены в таблице.
| Месяц | Число больных дизентерией (у) | Доля нестандартных проб воды (х) |
| Январь | 10 | 0 |
| Февраль | 9 | 0,5 |
| Март | 2 | 1,1 |
| Апрель | 7 | 2,0 |
| Май | 6 | 1,8 |
| Июнь | 11 | 2,9 |
| Июль | 26 | 6,7 |
| Август | 32 | 4,5 |
| Сентябрь | 46 | 8,7 |
| Октябрь | 38 | 7,1 |
| Ноябрь | 8 | 3,2 |
| Декабрь | 5 | 0 |
1. Создать таблицу данных «Анализ зависимости показателей» размером 2*12 в программе «Statistica». Внести данные (рисунок 10.1).
Рисунок 10.1. Ввод данных
2. Выбрать Statistics→Multiple regression (Множественная регрессия) (рисунок 10.2).
Рисунок 10.2. Выбор модуля «Multiple regression»
3. Задать переменные «Variables» (рисунок 10.3), в левом столбце «Dependent var.» (Зависимая переменная) выбрать «число больных дизентерией», в правом столбце «Independent variable list» (Перечень независимых переменных) выбрать «доля нестандартных проб воды», нажать кнопку «OK», а затем кнопку «Summary: Regression results».
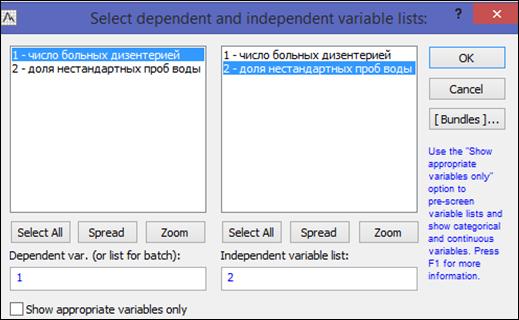
Рисунок 10.3. Задание переменных
На экране появится итоговая таблица (рисунок 10.4).
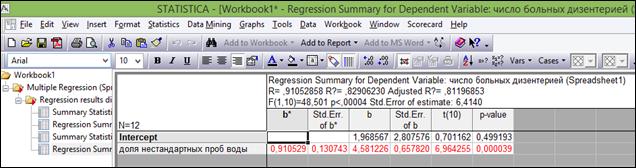
Рисунок 10.4. Итоговая таблица с результатами корреляционно-регрессионного анализа
В заголовке таблицы расположена следующая информация:
- R=0,91052858 – коэффициент корреляции;
- R2 =0,82906230– коэффициент детерминации;
- Adjusted R2 =0,81196853 – скорректированный коэффициент детерминации;
- F(1,10)=48,501 - значение F-критерия Фишера;
- число степеней свободы (1,10);
- р =0,0004 значение «р» для F-критерия Фишера;
- стандартная ошибка оценки 6,4140.
В таблице расположена следующая информация (по столбцам):
- значение коэффициент корреляции;
- стандартная ошибка коэффициент корреляции;
- точечные оценки параметров модели: коэффициент а=0,192, коэффициент b=0,181;
- стандартные ошибки коэффициентов регрессии;
- значение t-критерия;
- значение «р» для t-критерия.
Из приведенных результатов анализа можно сделать выводы:
· зависимость между показателями сильная и прямая, коэффициент корреляции достоверный;
· построенное уравнение статистически значимо;
· свободный член «а» статистически незначим, а коэффициент «b» статистически значим (выделен красным цветом).
Расчет коэффициента ранговой корреляции Спирмена в программе «Statistica».
Пример 10.2. Для данных из примера 10.1 рассчитать коэффициент ранговой корреляции Спирмена.
1. Создать таблицу данных «Анализ зависимости показателей» размером 2*12 в программе «Statisticа». Внести данные (рисунок 10.1).
2. Выбрать Statistics→Nonparametrics→Correlations (Spearman, Kendall tau, gamma) (рисунок 10.5), нажать кнопку «ОК».
Рисунок 10.5. Выбор процедуры «Correlations (Spearman, Kendall tau, gamma)»
3. Задать переменные «Variables» (рисунок 10.6), нажать кнопку «ОК».
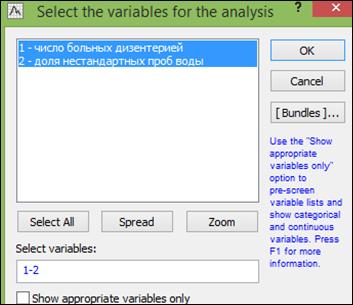
Рисунок 10.6. Задание переменных
4. Нажать кнопку «Spearman rank R» (Коэффициент Спирмена).
Результатом расчета коэффициента ранговой корреляции Спирмена является следующая таблица (рисунок 10.7).
Значение коэффициента ранговой корреляции 0,760071 указывает на то, что связь между признаками прямая и высокая.
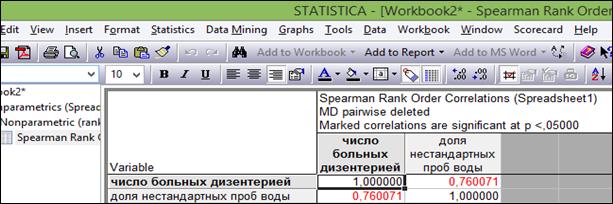
Рисунок 10.7. Результат расчета коэффициента ранговой корреляции Спирмена
6. Литература:
1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов / В.Е. Гмурман. - М.: Высшая школа, 2003. - 479 с.
2. Койчубеков Б.К. Биостатистика: Учебное пособие. - Алматы: Эверо, 2014. - 154 с.
3. Лобоцкая Н.Л. Высшая математика. / Н.Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. - Мн.: Высшая школа, 1987. - 319 с.
4. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах / Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
5. Основы высшей математики и математической статистики: Учебник / И.В. Павлушков и соавт. - М.: ГЭОТАР-МЕД, 2004. - 424 с.
6. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие / ред. Кучеренко В.З. - 4-е изд., перераб. и доп. – М.: ГЭОТАР - Медиа, 2011. - 256 с.
7. Боровиков В.П. STATISTICA. Искусство анализа данных на компьютере: для профессионалов / В. Боровиков. - СПб.: Питер, 2004. - 688 с.
8. Халафян А.А. Statistica 6. Статистический анализ данных. 3-е изд. Учебник - М.: ООО «Бином-Пресс», 2007. - 512 с.
9. http://www.statsoft.ru/
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №11
1. Тема: Стандартизированные коэффициенты. Прямой метод стандартизации.
2. Цель: Сравнение двух неоднородных совокупностей по какому-либо признаку с помощью прямого метода стандартизации.
3. Задачи обучения: Сформировать навыки сравнения двух неоднородных совокупностей по какому-либо признаку с помощью прямого метода стандартизации.
4. Основные вопросы темы:
1. Каковы условия применения метода стандартизации?
2. В чем заключается сущность метода стандартизации?
3. Что такое стандартизированные коэффициенты?
4. Какие методы вычисления стандартизированных коэффициентов существуют?
5. Какова последовательность этапов расчета стандартизованных коэффициентов при прямом методе стандартизации?
6. Что такое стандарт и как его получить?
5. Методы обучения и преподавания: письменное решение задач.
v Задания:
1. Ознакомиться с краткой теорией практического занятия №11.
2. Ответить на основные вопросы темы.
3. Выполнить пример 11.1.
4. Проанализировать показатели смертности на двух территориях РК, имеющих различие по возрастному составу населения с помощью метода стандартизации. В качестве стандарта принять возрастной состав населения на территории «С». Данные для расчета приведены в таблице.
| Возраст больных (в годах) | Территория «А» | Территория «Б» | Стандартное насе-ление территории «С» (доли) | ||
| Численность населения | Число умерших | Численность населения | Число умерших | ||
| До 19 | 30 000 | 150 | 10 000 | 40 | 0,25 |
| От 20 до 39 | 40 000 | 320 | 15 000 | 105 | 0,30 |
| От 40 до 59 | 40 000 | 600 | 20 000 | 240 | 0,20 |
| От 60 и старше | 20 000 | 600 | 25 000 | 625 | 0,25 |
| Всего | 130 000 | 1670 | 70 000 | 1010 | 1 |
5. Проанализировать показатели смертности на двух территориях РК, имеющих различие по возрастному составу населения с помощью метода стандартизации. В качестве стандарта принять возрастной состав населения на территории «С». Данные для расчета приведены в таблице.
| Возраст больных (в годах) | Территория «А» | Территория «Б» | Стандартное насе-ление территории «С» (доли) | ||
| Численность населения | Число умерших | Численность населения | Число умерших | ||
| До 19 | 50 000 | 300 | 20 000 | 100 | 0,25 |
| От 20 до 39 | 45 000 | 405 | 25 000 | 200 | 0,30 |
| От 40 до 59 | 40 000 | 640 | 30 000 | 390 | 0,20 |
| От 60 и старше | 30 000 | 960 | 35 000 | 980 | 0,25 |
| Всего | 165 000 | 2305 | 11 000 | 1670 | 1 |
6. Сравнить показатели летальности в двух группах больных СПИДом, получавших различные лекарственные препараты, с показателями, стандартизованными по тяжести течения заболевания. За стандарт принять сумму составов больных, получивших различное лечение. Данные для расчета показателей приведены в таблице.
| Тяжесть течения заболевания | Новое средство | Традиционное средство | ||
| Число больных | Из них умерло | Число больных | Из них умерло | |
| Очень тяжелое | 800 | 304 | 250 | 88 |
| Тяжелое | 400 | 120 | 200 | 70 |
| Средней тяжести | 300 | 81 | 300 | 105 |
| Легкое | 100 | 24 | 900 | 252 |
| Всего | 1600 | 529 | 1650 | 515 |
v Краткая теория
Метод стандартизации применяется при сравнении интенсивных показателей (например, общие показатели рождаемости, смертности, заболеваемости и др.) в совокупностях, отличающихся по составу (например, по возрасту, полу, профессиям и т.д.).
Данный метод позволяет устранить возможное влияние различий в составе совокупностей по какому-либо признаку на величину сравниваемых интенсивных показателей.
С этой целью составы совокупностей по данному признаку уравниваются, что в дальнейшем позволяет рассчитать стандартизованные коэффициенты.
Стандартизированные коэффициенты (показатели) - условные предположительные величины, свидетельствующие о том, каковы были бы значения сравниваемых интенсивных показателей, если бы были исключены различия в составе совокупностей.
Стандартизированные коэффициенты используют для сравнительного анализа уровней рождаемости, смертности, заболеваемости в неоднородных по возрастному и половому составу совокупностях.
Существуют следующие методы вычисления стандартизированных коэффициентов: прямой, косвенный, обратный.
Косвенный и обратныйметоды стандартизации применяют при отсутствии информации о возрастном составе умерших (родившихся) или о возрастной структуре населения. В настоящее время эти методы мало востребованы, поскольку имеется достаточно широкий доступ к получению данных для использования прямого метода стандартизации.
Прямой метод стандартизации применяется в случае, если известен возрастной состав населения и имеются данные для расчета возрастных коэффициентов смертности (рождаемости).
Этот метод состоит из следующих этапов:
1. Расчет общих и частных интенсивных показателей:
общих — по совокупностям в целом;
частных — по признаку различия (полу, возрасту, стажу работы и т.д.).
2. Определение стандарта, т.е. выбор одинакового численного состава среды по данному признаку (по возрасту, полу и т.д.) для сравниваемых совокупностей.
Как правило, за стандарт принимается сумма или полусумма численностей составов соответствующих групп. В то же время стандартом может стать состав любой из сравниваемых совокупностей, а также состав по аналогичному признаку какой-либо другой совокупности.
3. Вычисление ожидаемых абсолютных величин явления в группах стандарта на основе групповых интенсивных показателей, рассчитанных на 1-м этапе. Итоговые числа по сравниваемым совокупностям являются суммой ожидаемых величин в группах.
4. Вычисление стандартизированных показателей для сравниваемых совокупностей, используя итоговые ожидаемые величины в группах и новую среду-стандарт.
5. Сопоставление соотношений стандартизованных и интенсивных показателей, формулировка вывода.
Пример 11.1. Проанализировать показатели летальности в двух больницах «А» и «Б», имеющих различие по возрастному составу пациентов с помощью метода стандартизации, сделать выводы.
Данные для расчета показателей приведены в таблице.
| Возраст больных (в годах) | Больница «А» | Больница «Б» | ||
| Число выбывших больных | Из них умерло | Число выбывших больных | Из них умерло | |
| До 40 | 600 | 12 | 1400 | 42 |
| От 40 до 59 | 200 | 8 | 200 | 10 |
| От 60 и старше | 1200 | 60 | 400 | 24 |
| Всего | 2000 | 80 | 2000 | 76 |
1-Этап. Определить общие показатели летальности в больницах «А» и «Б».
Больница «А»: 80 - х
2000 - 100 80 × 100/2000 = 4 на 100 выбывших больных;
Больница «Б»: 76 - х
2000 - 100 76 × 100/2000 = 3,8 на 100 выбывших больных.
Найти показатели летальности в зависимости от возраста больных (частные показатели).
Например, в больнице «А» у больных в возрасте до 40 лет летальность составляет: 12 × 100/600 = 2%, а в больнице «Б»: 42 × 100/1400 = 3%.
Аналогично в других возрастных группах (таблица 10.1 - 1 этап).
2-Этап. Определить стандарт как сумму выбывших больных по каждой возрастной группе в обеих больницах.
| Возраст больных (в годах) | Число выбывших больных в больницах «А» и «Б» | Стандарт |
| До 40 | 600+1400 | 2000 |
| От 40 до 59 | 200+200 | 400 |
| От 60 и старше | 1200+400 | 1600 |
| Всего | 2000+20000 | 4000 |
3-Этап. Определить ожидаемое число умерших в стандарте по каждой возрастной группе в больницах «А» и «Б», с учетом соответствующих показателей летальности.
Возраст до 40 лет:
Больница «А» 100 - 2
2000 - х 2×2000/100 =40
Больница «Б» 100 - 3
2000 - х 3×2000/100=60
Возраст от 40 до 59 лет:
Больница «А» 100 - 4
400 - х 4×400/100 =16
Больница «Б» 100 - 5
400 - х 5×400/100=20
Возраст 60 лет и старше:
Больница «А» 100 - 5
1600 - х 5×1600/100 =80
Больница «Б» 100 - 6
1600 - х 6×1600/100=96
Найти сумму ожидаемых чисел умерших в стандарте в больнице «А»: (40 + 16 + 80 = 136) и больнице «Б»: (60 + 20 + 96 = 176).
4-Этап. Определить общие стандартизованные показатели летальности в больницах «А» и «Б».
Больница «А»: 136 × 100/4000 = 3,4 на 100 выбывших больных;
Больница «Б»: 176 × 100/4000 = 4,4 на 100 выбывших больных.
Результаты поэтапного расчета стандартизированных коэффициентов летальности оформить в виде таблицы (таблица 11.1).
Таблица 11.1.
| Возраст больных (в годах) | Больница «А» | Больница «Б» | 1 этап | 2 этап | 3 этап | ||||||
| Выбыло больных | Из них умерло | Выбыло больных | Из них умерло | Летальность на 100 выбывших больных | Стандарт (сумма составов больных обеих больниц) | Ожидаемое число умерших в стандарте | |||||
| Больница «А» | Больница «Б» | Больница «А» | Больница «Б» | ||||||||
| До 40 | 600 | 12 | 1400 | 42 | 2 | 3 | 2000 | 40 | 60 | ||
| От 40 до 59 | 200 | 8 | 200 | 10 | 4 | 5 | 400 | 16 | 20 | ||
| От 60 и старше | 1200 | 60 | 400 | 24 | 5 | 6 | 1600 | 80 | 96 | ||
| Всего | 2000 | 80 | 2000 | 76 | 4,0 | 3,8 | 4000 | 136 | 176 | ||
| 4 - этап Определение стандартизированных коэффициентов |
100 | 3,4 |
4,4
| ||||||||
5- Этап. Сопоставить соотношения интенсивных и стандартных показателей летальности в больницах «А» и «Б».
| Показатели | Больница «А» | Больница «Б» | Соотношение «А» и «Б» |
| Интенсивные | 4,0 | 3,8 | A>Б |
| Стандартизированные | 3,4 | 4,4 | A<Б |
Выводы:
1. Уровень летальности в больнице «А» выше, чем в больнице «Б».
2. Однако если бы возрастной состав выбывших больных в этих больницах был одинаков, то летальность была бы выше в больнице «Б».
3. Следовательно, на различия в уровнях летальности (в частности, на «завышение» ее в больнице «А» и «занижение» в больнице «Б») оказала влияние неоднородность возрастного состава больных, а именно, преобладание в больнице «А» пожилых пациентов (60 лет и более) с относительно высоким показателем летальности, и наоборот, в больнице «Б» — больных в возрасте до 40 лет, имеющих низкие показатели летальности.
6. Литература:
1. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие / ред. Кучеренко В.З. - 4-е изд., перераб. и доп. – М.: ГЭОТАР - Медиа, 2011. - 256 с.
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Занятие №12
1. Тема: Анализ динамических рядов. Типы динамических рядов. Вычисление показателей динамического ряда.
2. Цель: Анализ уровней динамического ряда для выводов о закономерностях и тенденциях явлений.
3. Задачи обучения: Сформировать навыки проведения анализа уровней динамического ряда для выводов о закономерностях и тенденциях явлений.
4. Основные вопросы темы:
1. Что такое динамический ряд? Из каких элементов он состоит? Какие типы динамических рядов Вы знаете?
2. Что такое тренд?
3. Какими способами осуществляется выравнивание динамического ряда?
4. Как определяются коэффициенты линейного тренда?
5. В чем разница между базисными и цепными показателями?
6. Какие относительные показатели динамики Вы знаете?
7. Какие средние показатели динамики Вы знаете?
5. Методы обучения и преподавания: письменное решение задач.
v Задания:
1. Ознакомиться с краткой теорией практического занятия №12.
2. Ответить на основные вопросы темы.
3. Изучена заболеваемость населения ветряной оспой за 10 лет (на 10 000 населения).
| Годы | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| Показатель | 3,5 | 4,9 | 3,6 | 5,7 | 6,5 | 5,5 | 8,1 | 7,2 | 5,0 | 7,3 |
На основании данного динамического ряда требуется:
1. Выровнять ряд по способу наименьших квадратов;
2. Изобразить графически исходный и выровненный ряды динамики;
3. Рассчитать показатели динамического ряда (абсолютный прирост, темп прироста) по сравнению с предыдущим годом и по сравнению с 2000 годом, а также абсолютное значение 1% прироста;
4. Рассчитать средние показатели динамического ряда (средний абсолютный прирост, средний коэффициент роста, средний темп прироста);
5. Сделать выводы о динамике явления по выровненным уровням.
4. Изучена заболеваемость населения гепатитом «В» за 10 лет (на 10 000 населения).
| Годы | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Показатель | 9,4 | 9,3 | 8,5 | 17,2 | 5,9 | 10,1 | 7,8 | 6,5 | 4,5 | 8,5 |
На основании данного динамического ряда требуется:
1. Выровнять ряд по способу наименьших квадратов;
2. Изобразить графически исходный и выровненный ряды динамики;
3. Рассчитать показатели динамического ряда (абсолютный прирост, темп роста, темп прироста) по сравнению с предыдущим годом и по сравнению с 2000 годом, а также абсолютное значение 1% прироста;
4. Рассчитать средние показатели динамического ряда (средний абсолютный прирост, средний коэффициент роста, средний темп прироста);
5. Сделать выводы о динамике явления по выровненным уровням.
v Краткая теория
Динамический (временной) ряд — совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.
Каждый временной ряд состоит из двух элементов:
1) моменты или периоды времени, к которым относятся приводимые статистические данные;
2) статистические показатели, которые характеризуют изучаемый объект на определенный момент или за указанный период времени.
Статистические показатели, характеризующие изучаемый объект, называют уровнями ряда.
Различают два типа динамических рядов: моментный и интервальный.
Моментный ряд — характеризует изменение размеров явления на определенную дату (момент).
Интервальный ряд — характеризует изменения размеров явления за определенный период (интервал времени).
Тренд - это функция от времени, определяющая основную тенденцию развития показателя во времени.
Для установления тренда динамический ряд выравнивают.
Выравнивание осуществляется следующими способами:
укрупнение периодов, расчет групповой средней, расчет скользящей средней, метод наименьших квадратов.
Метод наименьших квадратовприменяется для более точной количественной оценки динамики изучаемого явления:
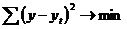 ,
,
где у - фактические (эмпирические) уровни ряда, yt - теоретические значения уровней ряда, т.е. вычисленные по соответствующему аналитическому уравнению на момент времени «t».
Обычно строят линейный тренд– это уравнение прямой линии, выражающее тенденцию изменения временного ряда, которое имеет вид:
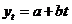 , (12.1)
, (12.1)
где a, b - коэффициенты, рассчитываемые по формулам:
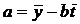 ,
, 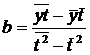 . (12.2)
. (12.2)
Подставляя последовательно в уравнение 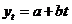 значения «t», находят теоретические значения уровней ряда.
значения «t», находят теоретические значения уровней ряда.
Анализ скорости и интенсивности развития явлений во времени осуществляется с помощью статистических показателей, которые получаются в результате сравнения уровней между собой.
К таким показателям относятся: абсолютный прирост, темп прироста, абсолютное значение одного процента прироста.
При этом принято сравниваемый уровень называть отчетным, а уровень, с которым производится сравнение - базисным.
Показатели динамики с постоянной базой (базисные показатели) характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относится базовый уровень, до данного (i-го) периода.
Показатели динамики с переменной базой (цепные показатели)характеризуют интенсивность изменения уровня от периода к периоду в пределах изучаемого промежутка времени.
1. Абсолютный прирост (Δi) - показатель, определяемый как разность между двумя уровнями динамического ряда. Он показывает, на сколько данный уровень ряда превышает уровень, принятый за базу сравнения:
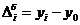 , (12.3)
, (12.3)
где 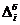 - абсолютный базисный прирост; уi - уровень сравниваемого периода; у0 - уровень базисного периода.
- абсолютный базисный прирост; уi - уровень сравниваемого периода; у0 - уровень базисного периода.
При сравнении с переменной базой абсолютный прирост будет равен:
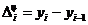 , (12.4)
, (12.4)
где уi-1 - уровень непосредственно предшествующего периода.
Абсолютный прирост с переменной базой называют скоростью роста.
2. Коэффициент роста определяется как отношение двух сравниваемых уровней и показывает, во сколько раз данный уровень превышает уровень базисного периода:
базисный 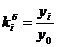 ; цепной
; цепной 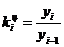 . (12.5)
. (12.5)
3. Если коэффициенты роста выражают в процентах, то их называют темпами роста, т.е. они характеризуют скорость изменения показателя в единицу времени, выраженную в процентах: 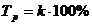 .
.
4. Темп приростапоказывает, на сколько процентов уровень данного периода больше (или меньше) базисного уровня. Этот показатель может быть рассчитан двояко:
как отношение абсолютного прироста к базисному уровню:
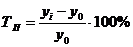 или
или 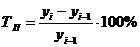 . (12.6)
. (12.6)
как разность между темпом роста (в %) и 100% :
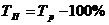 . (12.7)
. (12.7)
5. Чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста.
Результат выражают показателем, который называют абсолютным значением одного процента прироста (Аi):
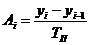 . (12.8)
. (12.8)
6. При сопоставлении динамики развития двух явлений можно использовать показатели, представляющие собой отношения темпов прироста за одинаковые отрезки времени по двум динамическим рядам.
Эти показатели называют коэффициентами опережения:
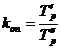 или
или 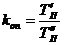 , (12.9)
, (12.9)
где 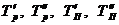 - соответственно темпы роста и темпы прироста сравниваемых динамических рядов.
- соответственно темпы роста и темпы прироста сравниваемых динамических рядов.
С помощью этих коэффициентов могут сравниваться:
- ряды одинакового содержания, но относящиеся к разным территориям (странам, регионам, районам и т.п.) или различным организациям;
- ряды разного содержания, характеризующие один и тот же объект.
Для обобщающей характеристики динамики исследуемого явления за ряд периодов определяют различного рода средние показатели.
1. Средний абсолютный прирост - средняя величина изменения показателя за интервал времени.
Рассчитывается как средняя арифметическая величина из показателя скорости роста за отдельные промежутки времени:
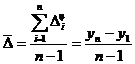 , (12.10)
, (12.10)
где n - число уровней ряда; 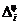 - абсолютные изменения по сравнению с предшествующим уровнем.
- абсолютные изменения по сравнению с предшествующим уровнем.
Средний абсолютный прирост дает возможность рассчитать, на сколько в среднем за единицу времени должен увеличиваться уровень ряда.
2. Средний темп роста– это характеристика интенсивности изменения уровней ряда динамики. Он показывает во сколько раз в среднем за единицу времени изменился уровень динамического ряда:
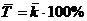 , (12.11)
, (12.11)
где 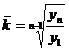 - средний коэффициент роста; n- число уровней ряда.
- средний коэффициент роста; n- число уровней ряда.
3. Средний темп прироставычисляется по следующей формуле:
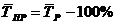 . (12.12)
. (12.12)
6. Литература:
1. Койчубеков Б.К. Биостатистика: Учебное пособие. - Алматы: Эверо, 2014. - 154 с.
2. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах / Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
3. Применение методов статистического анализа для изучения общественного здоровья и здравоохранения: учебное пособие / ред. Кучеренко В.З. - 4-е изд., перераб. и доп. – М.: ГЭОТАР - Медиа, 2011. - 256 с.
7. Контроль:
v Выполнение тестовых заданий на компьютере.
Приложение 1
Таблица значений функции распределения нормированного нормального распределения
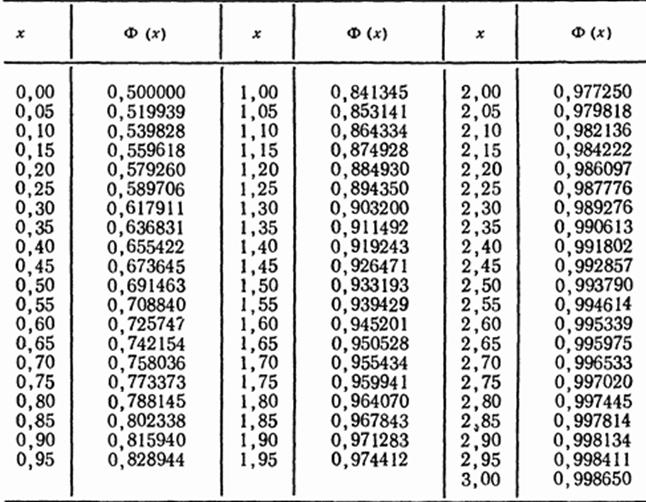
Приложение 2
Таблица критических значений критерия χ2-Пирсона
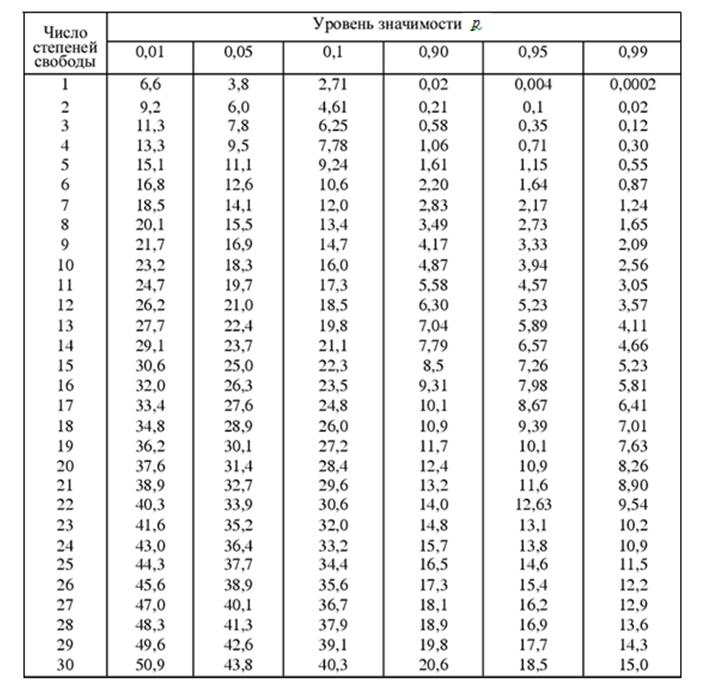

Приложение 3
Таблица значений функции Лапласа
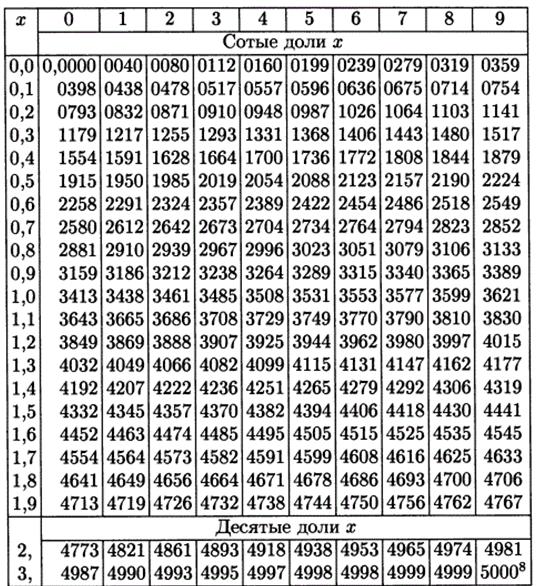
Приложение 4
Таблица критических значений F-критерия Фишера при р=0,05
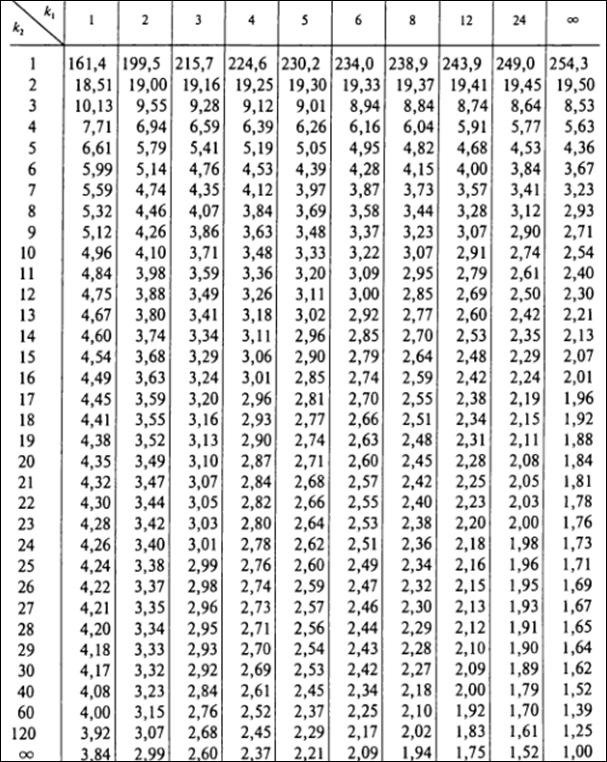
Приложение 5
Таблица критических значений t-критерия Стьюдента
| Число степеней свободы | Уровень значимости, р | |||
| f | 0,10 | 0,05 | 0,02 | 0,01 |
| 1 | 6,31 | 12,7 | 31,82 | 63,7 |
| 2 | 2,92 | 4,30 | 6,97 | 9,92 |
| 3 | 2,35 | 3,18 | 4,54 | 5,84 |
| 4 | 2,13 | 2,78 | 3,75 | 4,60 |
| 5 | 2,01 | 2,57 | 3,37 | 4,03 |
| 6 | 1,94 | 2,45 | 3,14 | 3,71 |
| 7 | 1,89 | 2,36 | 3,00 | 3,50 |
| 8 | 1,86 | 2,31 | 2,90 | 3,36 |
| 9 | 1,83 | 2,26 | 2,82 | 3,25 |
| 10 | 1,81 | 2,23 | 2,76 | 3,17 |
| 11 | 1,80 | 2,22 | 2,72 | 3,11 |
| 12 | 1,78 | 2,18 | 2,68 | 3,05 |
| 13 | 1,77 | 2,16 | 2,65 | 3,01 |
| 14 | 1,76 | 2,14 | 2,62 | 2,98 |
| 15 | 1,75 | 2,13 | 2,60 | 2,95 |
| 16 | 1,75 | 2,12 | 2,58 | 2,92 |
| 17 | 1,74 | 2,11 | 2,57 | 2.90 |
| 18 | 1,73 | 2,10 | 2,55 | 2,88 |
| 19 | 1,73 | 2,09 | 2,54 | 2,86 |
| 20 | 1,73 | 2,09 | 2,53 | 2,85 |
| 30 | 1,70 | 2,04 | 2,46 | 2,75 |
| 40 | 1,68 | 2,02 | 2,42 | 2,70 |
| 60 | 1,67 | 2,00 | 2,39 | 2,66 |
| 120 | 1,66 | 1,98 | 2,36 | 2,62 |
| ¥ | 1,64 | 1,96 | 2,33 | 2,58 |
Приложение 6
Таблица критических значений U-критерия Манна-Уитни
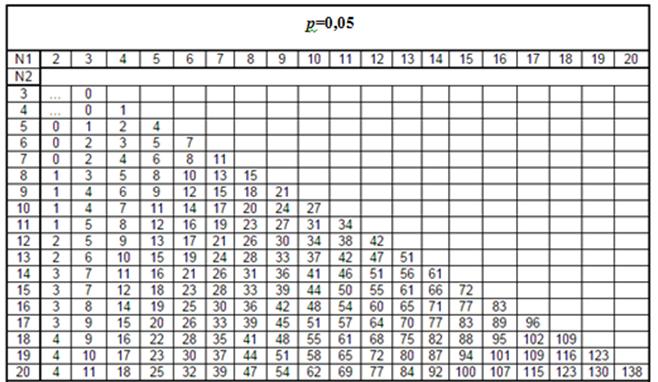
Приложение 7
Таблица критических значений W-критерия Уилкоксона
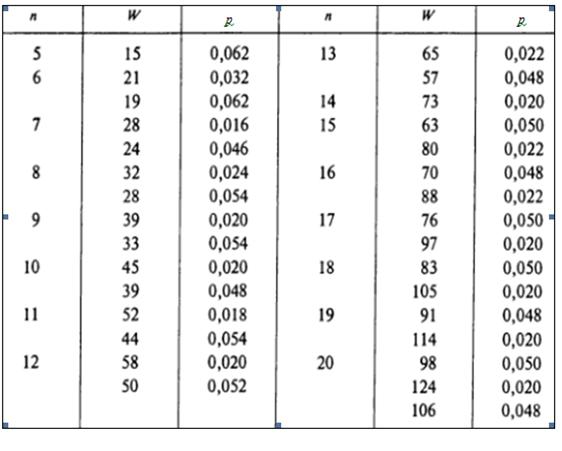
Приложение 8
Таблица критических значений Н-критерия Крускала-Уоллиса
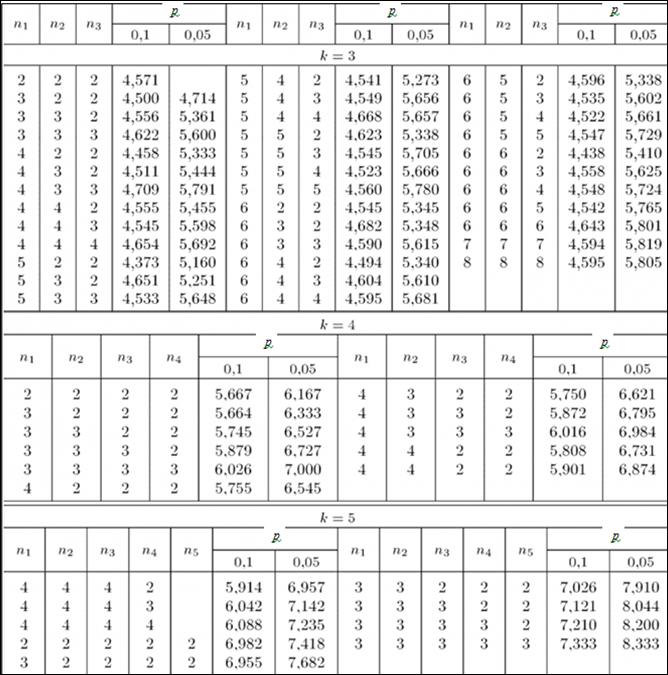
Дата добавления: 2018-04-05; просмотров: 3867; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
