Элементарные оптимизационные задачи

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Все дети и подростки, руководствуются в своих действиях какими-либо достаточно простыми сиюминутными желаниями, не очень задумываясь об отдаленных результатах и последствиях этих действий, а также о способах их осуществления. Во взрослом мире деятельность практически всегда не просто осознанная, а целенаправленная, какая-то работа совершается ради достижения определенной цели. Конечно, практически всегда ресурсы, необходимые для выполнения данной работы, ограничены. Достаточно часто существует несколько возможностей распорядиться ресурсами, и хотелось бы сделать это в каком-то смысле «получше». Если ситуация несколько сложнее, то бывает очень трудно найти способ действия, возникает потребность в использовании специальных методов. Исследование операции как раз и занимается этим кругом вопросов:

- цель работы;

- ограниченность необходимых ресурсов;

- поиск вариантов возможных решений;

- определение способа действий.

Поскольку речь идет о количественных величинах, постольку нужны достаточно формализованные понятия. В исследовании операций для выработки вариантов решений их анализа и сравнения используются математические описания объектов исследования и процессов, то есть математические модели.

Цель – это желаемый результат деятельности. Результат принятого решения стараются описать функцией, аргументами которой являются разные варианты решений, а значениями – числа, отражающие меру достижения цели. Эту функцию называют целевой функцией, или критерием, а лучшим будет то решение, которое делает значение целевой функции большим или меньшим (исходя из ее смысла).

Среди вариантов решений только некоторые удовлетворяют ограничениям, не нарушают их. Такие решения называются допустимыми. Допустимое решение, которое доставляет максимум (или минимум) целевой функции, называется оптимальным.

В дальнейшем будем использовать такие обозначения:
F(x) – целевая функция скалярного или векторного аргумента х;
Х – допустимое множество;
– имеет обычный смысл (х принадлежит Х, является одним из элементов Х);
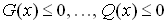– функциональные ограничения, описывающие взаимосвязи переменных.

Найти то значение переменной, которое доставляет экстремум (максимум или минимум) целевой функции, и величину целевой функции при этом значение означает решить данную оптимизационную задачу. В стационарной форме оптимизиционную задачу максимизации можно записать так:

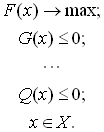
От переменной х часто требуется неотрицательность. В некоторых случаях с помощью искусственного добавления переменных функциональные неравенства можно превращать в уравнения. Совпадения числа переменных с числом уравнений не требуется (рисунок 1).

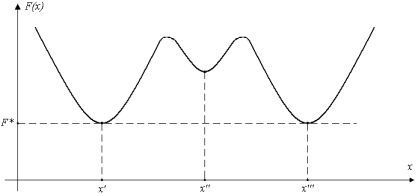
Рисунок 1

Оптимальное решение может быть не единственным или отсутствовать. Если оптимальное решение – не единственное, то есть существует несколько решений, которые доставляют экстремум целевой функции, то значение целевой функции для всех этих решений одно и то же. Это означает, что прилагательные «оптимальный» не имеет степеней сравнения. Решение оптимальное по одному критерию, может не быть оптимальным по другому критерию.

Наконец, отметим совпадение решений задач (то есть значений переменных) с целевыми функциями: 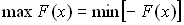. Это видно из рисунка 2.

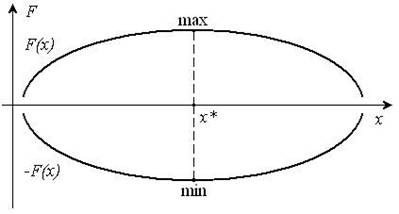
Рисунок 2

Эффект – это результат деятельности, эффективность – это соизмерение результата и затрат.

Основные этапы работы с оптимизационными задачами:

1. Постановка задачи, то есть ее содержательная формулировка с точки зрения и заказчика и разработчика.

2. Построение математической модели, то есть переход к формализованному представлению, общий вид которого приведен выше.

3. Нахождение решения или решений (нахождение какого-либо решения или всех оптимальных и близких к нему решений – это разные задачи и по постановке, и по методам, и по сложности, и по результативности получаемых вариантов).

4. Проверка модели и полученного с его помощью решения. Это – необходимый этап, так как модель лишь частично отображает действительность. Хорошая модель должна точно предсказывать влияние изменений в реальной системе на общую эффективность решений.

5. Построение процедуры подстройки модели, поскольку в модели могут изменяться какие-либо неуправляемые переменные.

6. Выбор вариантов, если есть несколько конкурирующих вариантов.

7. Осуществление решения.

Как правило, перечисленные этапы перекрываются, идут параллельно или несколько раз циклически повторяются.

Пусть есть несколько целевых функций 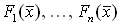каждую из которых хотят максимизировать.

Вектор решения 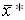называют эффективным, если не существует другого вектора 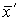, для которого значения всех функций 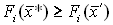и хотя бы одно неравенство – строгое. Суть в том, что есть несколько (эффективных) решений, которые несравнимы: одно решение в чем-то лучше по одному из критериев, но хуже по другому, и нет такого вектора, которых был бы лучше сразу по всем критериям.

Множество эффективных векторов называют множеством Парето, а любой вектор этого множества – оптимумом по Парето.

Для того чтобы разобраться в понятии «эффективное решение», посмотрим, что такое неэффективное решение. Решение А – неэффективное, если есть решение В такое, что В лучше А сразу по всем критериям. Надо иметь в виду, что решение может быть либо эффективным, либо неэффективным.

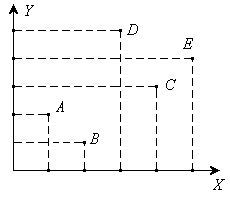
Рисунок 3

В качестве примера рассмотрим простую ситуацию. Человек собирается приобрести легковой автомобиль. Каждый вариант он оценивает по двум критериям: Х – популярность автомобиля, Y – ходовые качества. Результаты его анализа представлены на рисунке. Варианты А и В – неэффективные, так как вариант С лучше, чем А и В сразу по двум критериям. Вариант С – также неэффективный, так как вариант Е лучше С сразу по двум критериям. Эффективными являются варианты D и Е (рисунок 3). Если человек захочет сделать выбор между этими вариантами, то ему надо либо бросить жребий, либо принять во внимание какие-либо дополнительные соображения (например, расход бензина).

Дата добавления: 2018-04-05; просмотров: 293; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!