Арифметическое п-мерное пространство. Скалярное произведение и его свойства.
Величина, которая полностью характеризуется своим числовым значением в выбранной системе единиц, называется скалярной или скаляром (масса, объем, температура). Скаляр определяется числом, положительным, отрицательным или равным нулю. Если величина характеризуется еще и направлением, то она называется векторной или вектором (сила, скорость и так далее). Таким образом, вектор определяется числом и направлением.
Многие вопросы как теоретического, так и прикладного характера приводят к рассмотрению упорядоченных совокупностей чисел (величин). Например, план работы предприятия, выраженный в определенных числовых показателях, рост цен за ряд лет и так далее. Если отвлечься от конкретного смысла объектов, мы приходим к следующему понятию.
Определение 1.1. Множество всех упорядоченных совокупностей по n чисел ( 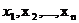 ) называется арифметическим n-мерным пространством (
) называется арифметическим n-мерным пространством (  ) , n - размерность пространства.
) , n - размерность пространства.
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними

где  - угол между векторами,
- угол между векторами,  ,
,  - модули (длины) векторов
- модули (длины) векторов
Скалярное произведение векторов можно выразить также формулами

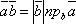
Скалярное произведение  называется скалярным квадратом вектора и обозначается символом
называется скалярным квадратом вектора и обозначается символом 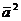 . Скалярный квадрат вектора равен квадрату его модуля:
. Скалярный квадрат вектора равен квадрату его модуля:  .
.
Если векторы и заданы своими координатами:  ,
, 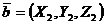 , то их скалярное произведение можно вычислить по формуле:
, то их скалярное произведение можно вычислить по формуле: 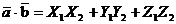
|
|
|
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов: 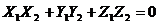
Угол между векторами (сторонами, прямыми): 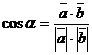
Длина (модуль) вектора: 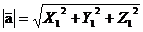 ,
, 
Свойства скалярного произведения:
1. 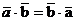 (коммутативность)
(коммутативность)
2. 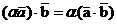
3. 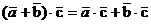
20. Ранг матрицы. Обратная матрица и ее вычисление.
Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Обычно ранг матрицы A обозначается rang A.
Наиболее распространенный метод нахождения ранга матрицы – метод элементарных преобразований – ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
Метод окаймляющих миноров: Пусть в матрице A найден ненулевой минор k-го порядка M. Рассмотрим все миноры (k + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.
|
|
|
Обратная матрица — такая матрица 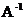 , при умножении на которую исходная матрица A даёт в результате единичную матрицу E.
, при умножении на которую исходная матрица A даёт в результате единичную матрицу E.

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.
Формула для нахождения обратной матрицы:
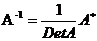
Где 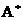 - матрица, присоединенная к матрице А (союзная), состоящая из алгебраических дополнений к элементам матрицы А.
- матрица, присоединенная к матрице А (союзная), состоящая из алгебраических дополнений к элементам матрицы А.
Вычеркнем из определителя n-го порядка i-ю строку и к-й столбец. Оставшееся выражение порождает определитель (n-1)-го порядка 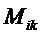 , называемый минором элемента
, называемый минором элемента 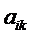 . Величина
. Величина  называется алгебраическим дополнением элемента
называется алгебраическим дополнением элемента 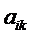 .
.
Итак, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.
21. Элементарные преобразования матриц. Формулировка теоремы Кронекера-Капелли.
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
|
|
|
Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.
Элементарные преобразования: разрешается изменять порядок строк (что соответствует изменению порядка уравнений); умножать строки на любое отличное от нуля число (что соответствует умножению соответствующих уравнений на это число); прибавлять к любой строке матрицы В любую другую ее строку, умноженную на любое число (что соответствует прибавлению к одному из уравнений системы другого уравнения, умноженного на это число). С помощью таких преобразований каждый раз получается расширенная матрица новой системы, равносильная исходной. При этом стараются привести расширенную матрицу системы к ступенчатому виду, из которого решение системы видно непосредственно.
Возможные варианты решения:
*если ранг расширенной матрицы равен рангу матрицы коэффициентов и равен числу неизвестных, то система совместна определенна, т.е. имеет единственное решение;
|
|
|
*если ранг расширенной матрицы равен рангу матрицы коэффициентов и меньше числе неизвестных, то система совместна неопределенна, т.е. имеет множество решений;
*если ранги не равны, то система несовместна, т.е. не имеет решений.
Теорема Кронекера — Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.
Совместная система будет определена (её решение единственно), если ранги равны числу неизвестных.
22. Решение систем линейных уравнений матричным методом.
С помощью обратной матрицы можно решать матричным способом линейные системы.
Пусть дана система n линейных уравнений с n неизвестными (1)
 (1)
(1)
Введем матрицы

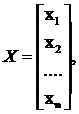
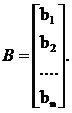
Тогда в матричной форме система (1) запишется в виде
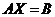
Пусть 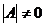 , тогда
, тогда 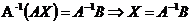
Формула 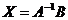 является матричной записью решения системы (1).
является матричной записью решения системы (1).
23. Определение функции
Функция-зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у, где переменная х – независимая переменная или аргумент и переменная у – зависимая переменная.
Способы задания функций
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции.
Табличный способ заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако его преимущество – наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания. Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Дата добавления: 2018-04-05; просмотров: 438; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
