Операторный метод анализа переходных процессов
Если для классического метода анализа колебаний в линейных электрических цепях с сосредоточенными элементами при произвольных воздействиях сводится к решению неоднородной системы обыкновенных линейных дифференциальных уравнений при заданных начальных условиях, то для аналитического решения этих уравнений в теории электрических цепей нашли широкое применение операторные методы. Операторный метод анализа позволяет сводить линейные дифференциальные уравнения к более простым алгебраическим уравнениям что в ряде случаев упрощает расчеты. Его идея заключается в том, что расчет переходного процесса переносится из области функций действительной переменной (времени t) в область функций комплексной переменной р. Такое преобразование называется прямым.
В настоящее время операторные методы связывают с применением преобразования Лапласа:
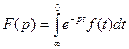 ,где f(t) – однозначная функция времени, называемая оригиналом; F(p) – функция комплексной переменной р, называемая лапласовым изображением.
,где f(t) – однозначная функция времени, называемая оригиналом; F(p) – функция комплексной переменной р, называемая лапласовым изображением.
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНОЙЭЛЕКТРИЧЕСКОЙ ЦЕПИ
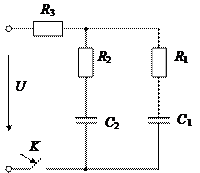
Заданы разветвленные электрические цепи: с одним и двумя реактивными элементами; с нулевыми или ненулевыми начальными условиями. На всех схемах указан вид коммутации, вызывающий переходный процесс.
Параметры элементов схем, приведенных на рисунках, выбираются из таблицы 1.
Требуется:
1. Рассчитать переходный процесс в заданной цепи классическим методом.
|
|
|
2. Рассчитать переходный процесс в заданной цепи операторным (либо другим указанным преподавателем) методом.
3. Построить графики изменения во времени токов в ветвях цепи и напряжений на реактивных элементах.
Варианты курсовой работы
Параметры элементов электрической цепи Таблица 1
| № варианта | U | R1 | R2 | R3 | L1 | L2 | C1 | C2 |
| В | Ом | Гн | мкФ | |||||
| 1 | 200 | 100 | 50 | 200 | 1,0 | 0,5 | 50 | 100 |
| 2 | 100 | 125 | 75 | 50 | 0,4 | 0,2 | 20 | 40 |
| 3 | 120 | 100 | 100 | 125 | 0,2 | 0,1 | 20 | 40 |
| 4 | 50 | 150 | 75 | 50 | 0,5 | 0,2 | 25 | 50 |
| 5 | 75 | 50 | 75 | 125 | 0,2 | 0,1 | 0,2 | 0,1 |
| 6 | 50 | 800 | 1000 | 1000 | 0,25 | 0,5 | 0,2 | 0,1 |
| 7 | 75 | 800 | 2000 | 1000 | 0,25 | 0,5 | 0,1 | 0,2 |
| 8 | 100 | 1500 | 500 | 1000 | 0,4 | 0,8 | 0,1 | 0,2 |
| 9 | 120 | 50 | 125 | 50 | 0,2 | 0,4 | 20 | 10 |
| 10 | 200 | 200 | 125 | 50 | 0,4 | 0,2 | 125 | 80 |
| 11 | 240 | 100 | 50 | 200 | 0,5 | 1,0 | 50 | 125 |
| 12 | 240 | 200 | 100 | 100 | 0,1 | 0,5 | 100 | 50 |
| 13 | 50 | 800 | 1000 | 2000 | 0,25 | 0,50 | 0,1 | 0,2 |
| 14 | 240 | 200 | 100 | 100 | 0,8 | 0,4 | 100 | 50 |
| 15 | 150 | 50 | 125 | 50 | 0,4 | 0,2 | 10 | 20 |
| 16 | 150 | 50 | 125 | 50 | 0,2 | 0,4 | 20 | 10 |
| 17 | 100 | 100 | 50 | 100 | 0,5 | 0,1 | 100 | 50 |
| 18 | 100 | 200 | 100 | 100 | 0,4 | 0,8 | 80 | 125 |
| 19 | 110 | 800 | 1000 | 1000 | 0,5 | 0,25 | 0,1 | 0,2 |
| 20 | 50 | 800 | 1000 | 2000 | 0,25 | 0,5 | 0,2 | 0,1 |
| 21 | 110 | 125 | 50 | 75 | 0,2 | 0,1 | 40 | 20 |
| 22 | 100 | 125 | 50 | 100 | 0,1 | 0,2 | 20 | 40 |
| 23 | 50 | 100 | 50 | 100 | 0,5 | 0,1 | 50 | 100 |
| 24 | 50 | 100 | 50 | 100 | 0,5 | 1,0 | 125 | 80 |
| 25 | 50 | 100 | 50 | 200 | 0,5 | 1,0 | 100 | 50 |
| 26 | 50 | 800 | 1000 | 2000 | 0,25 | 0,5 | 0,1 | 0,2 |
| 27 | 50 | 800 | 2000 | 1000 | 0,25 | 0,5 | 0,2 | 0,1 |
| 28 | 50 | 1000 | 800 | 2000 | 0,25 | 0,5 | 0,2 | 0,1 |
| 29 | 50 | 2000 | 800 | 1000 | 0,25 | 0,5 | 0,2 | 0,1 |
| 30 | 50 | 2000 | 800 | 1000 | 0,5 | 0,25 | 0,1 | 0,2 |
| 31 | 50 | 800 | 1000 | 1000 | 0,25 | 0,5 | 0,2 | 0,1 |
| 32 | 50 | 800 | 1000 | 1000 | 0,25 | 0,5 | 0,2 | 0,1 |
| 33 | 50 | 800 | 1000 | 1000 | 0,25 | 0,5 | 0,2 | 0,1 |
| 34 | 100 | 1000 | 1000 | 2000 | 0,5 | 0,25 | 0,1 | 0,2 |
| 35 | 100 | 2000 | 1000 | 1000 | 0,4 | 0,8 | 0,05 | 0,1 |
| 36 | 100 | 1000 | 1000 | 2000 | 0,4 | 0,8 | 0,05 | 0,1 |
| 37 | 100 | 1000 | 2000 | 1000 | 0,4 | 0,8 | 0,1 | 0,05 |
| 38 | 100 | 2000 | 1000 | 2000 | 0,8 | 0,4 | 0,1 | 0,05 |
| 39 | 100 | 1200 | 2000 | 1000 | 0,8 | 0,4 | 0,05 | 0,1 |
| 40 | 200 | 100 | 0 | 200 | 1,0 | 0 | 50 | 0 |
| 41 | 150 | 50 | 0 | 50 | 0,4 | 0 | 10 | 0 |
| 42 | 120 | 200 | 125 | 75 | 0,2 | 0 | 50 | 0 |
| 43 | 50 | 150 | 75 | 50 | 0,5 | 0 | 25 | 0 |
| 44 | 120 | 200 | 125 | 0 | 0,2 | 0 | 50 | 0 |
| 45 | 240 | 200 | 100 | 0 | 0,4 | 0 | 125 | 0 |
| 46 | 120 | 50 | 125 | 0 | 0,2 | 0 | 20 | 0 |
| 47 | 240 | 0 | 50 | 200 | 1,0 | 0 | 100 | 0 |
| 48 | 120 | 125 | 0 | 75 | 0,2 | 0 | 50 | 0 |
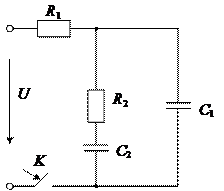

|
|
|
Рис.1 Рис.2 Рис.3
|
|
|



Рис.4 Рис.5 Рис.6



Рис.7 Рис.8 Рис.9



Рис.10 Рис.11 Рис.12



Рис.13 Рис.14 Рис.15



Рис.16 Рис.17 Рис.18
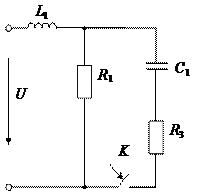


Рис.19 Рис.20 Рис.21



Рис.22 Рис.23 Рис.24



Рис.25 Рис.26 Рис.27


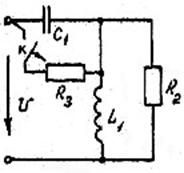
Рис.28 Рис.29 Рис.30

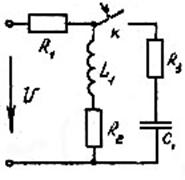
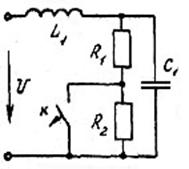
Рис.31 Рис.32 Рис.33


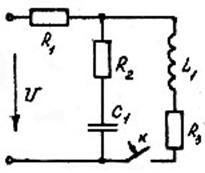
Рис.34 Рис.35 Рис.36
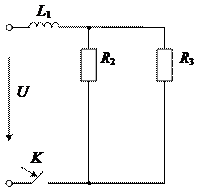

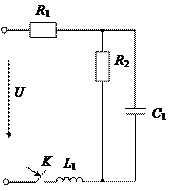
Рис.37 Рис.38 Рис.39
|
|
|


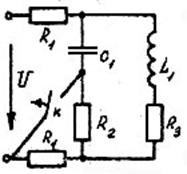
Рис.40 Рис.41 Рис.42
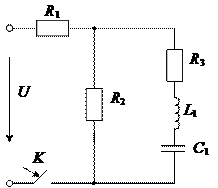

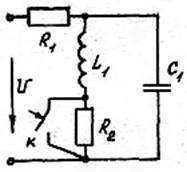
Рис.43 Рис.44 Рис.45

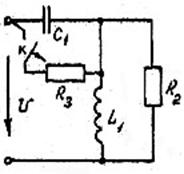

Рис.46 Рис.47 Рис.48
ПРИМЕР РАСЧЕТА
Рассчитаем цепь, показанную на рис. 4.79. Численные данные для данной схемы приведены в табл. 4.2.
Таблица 4.2
| U0 | R0 | R1 | R2 | L | C |
| В | Ом | Ом | Ом | Гн | мкФ |
| 150 | 100 | 300 | 200 | 0,1 | 10 |
Классический метод

|
| Рис. 4.79 |
1. Пусть 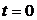 – момент коммутации.
– момент коммутации.
2. Ток 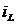 выбираем в качестве искомой переменной, т.к. этот ток подчиняется законам коммутации.
выбираем в качестве искомой переменной, т.к. этот ток подчиняется законам коммутации.
3. Рассчитаем токи до коммутации, т.е. при 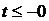 . Цепь содержит резистор
. Цепь содержит резистор 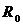 . Постоянный ток через конденсатор не проходит, поэтому
. Постоянный ток через конденсатор не проходит, поэтому 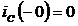 ,
, 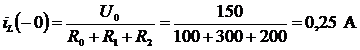 ,
, 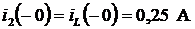 ,
,  .
.
4. Используя законы Кирхгофа, запишем уравнения для времени после коммутации 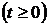
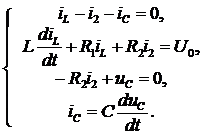 (4.1)
(4.1)
Приведем данную систему к одному дифференциальному уравнению, в котором фигурировала бы только одна переменная – ток  (или напряжение
(или напряжение 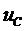 ). Так как эти переменные не изменяются в момент коммутации, то при решении дифференциального уравнения в качестве начальных условий можно использовать их значения, которые они принимают до коммутации (
). Так как эти переменные не изменяются в момент коммутации, то при решении дифференциального уравнения в качестве начальных условий можно использовать их значения, которые они принимают до коммутации ( 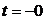 ). Исключая переменные
). Исключая переменные 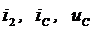 , из системы (4.1) получим требуемое дифференциальное уравнение второго порядка:
, из системы (4.1) получим требуемое дифференциальное уравнение второго порядка:
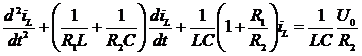 . (4.2)
. (4.2)
Решение уравнения (4.2) ищем в виде: 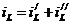 , где
, где 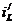 – значение тока в новом установившемся режиме,
– значение тока в новом установившемся режиме, 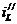 – свободная составляющая тока.
– свободная составляющая тока.
5. Рассчитаем новый установившийся режим цепи ( 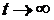 ):
):
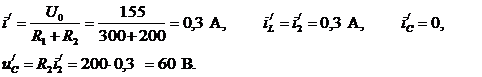
6. Найдем начальные условия для искомой переменной и ее производной: 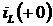 и
и 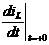 . Согласно законам коммутации имеем
. Согласно законам коммутации имеем

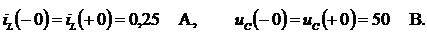
После подстановки этих величин в систему (4.1), записанную для момента времени  , получим систему алгебраических уравнений относительно переменных:
, получим систему алгебраических уравнений относительно переменных:
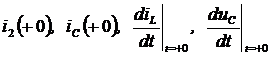 .
.

Решая эту систему, определим недостающее начальное условие:
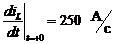 (4.3)
(4.3)
Одновременно найдем: 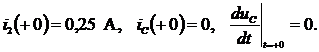
7. Подставим численные данные в уравнение (4.2) и решим его
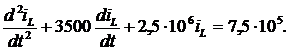 (4.4)
(4.4)
Решение неоднородного дифференциального уравнения (4.4) запишем как сумму частного решения  и общего решения
и общего решения 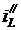 однородного уравнения:
однородного уравнения:
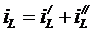 . (4.5)
. (4.5)
Решение однородного уравнения, называемое свободным током, записывается следующим образом:
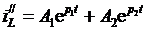 . (4.6)
. (4.6)
где  и
и  – постоянные интегрирования;
– постоянные интегрирования; 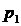 и
и 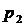 – корни характеристического уравнения:
– корни характеристического уравнения:

Решаем это уравнение и находим:
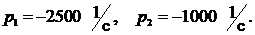
Дата добавления: 2018-04-05; просмотров: 1232; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
