Выпуклость графика функции. Точки перегиба
Понятие числовой функции, ее простейшие свойства
Задать на некотором числовом множестве функцию у = f(x) – это значит указать правило, которое каждому числу x из этого множества ставит в соответствие одно определенное число у, называемое значением функции. Множество чисел, на котором задана функция, называется областью определения функции.
Существуют различные способы задания функций: аналитический, графический, табличный, словесный. При аналитическом способе задания функции под ее областью определения (если она не указана) понимается множество всех тех значений х, при которых формула, определяющая функцию, имеет смысл.
График функции у = f(х) — это множество точек координатной плоскости вида (х; f(х)), где х — произвольное число из области определения функции.
Функция у = f(х) называется четной (нечетной), если для каждого х из области определения функции число -х также принадлежит ее области определения и выполняется равенство f(-x)=f(x) f(-x)=-f(x)
График четной функции симметричен относительно оси ординат, а нечетной — относительно начала координат.
Функция у = f(х) называется периодической, если существует такое число Т≠О, что для каждого х из области определения функции значения х + Т и х — Т также принадлежат ее области определения, и при этом выполняются равенства f (x-T) = f(x) = f(x+T)
Число Т называется периодом функции у = f(x).
Функция у=f(х) называется возрастающей (убывающей) на множестве X, если для любых х1 и x2 из этого множества и таких, что х2>х1, выполняется f(x2)>f(x1) (f(x2)<f(x1)). Если функция возрастает (убывает) на всей области определения, то говорят, что у = f(х) возрастающая (убывающая) функция. Возрастающие и убывающие функции называются монотонными.
|
|
|
Возрастание и убывание функции. Точки экстремума
С помощью производной можно находить промежутки возрастания и убывания функции.
Признаки возрастания и убывания функции:
1. Если  , то функция
, то функция  возрастает в т. x0 .
возрастает в т. x0 .
2. Если 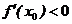 , то функция
, то функция  убывает в т. x0 .
убывает в т. x0 .
Для нахождения интервалов монотонности рекомендуется:
1. Найти область определения функции, если она не указана.
2. Найти производную и критические точки функции, т.е. точки из области определения функции, в которых ее производная равна нулю или не существует. Критическими точками область определения функции разбивается на интервалы, на каждом из которых производная сохраняет свой знак.
3. Установить знак производной на каждом из найденных интервалов. Если на рассматриваемом интервале производная функции положительна (отрицательна), то на этом интервале функция возрастает (убывает).
|
|
|
Пример 2.1. Найти интервалы возрастания и убывания функции.

Решение. Функция определена и дифференцируема на интервале (1; +∞). Найдем ее производную:
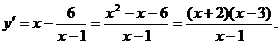
Уравнение 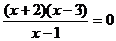 имеет два корня x1= -2 и х2= 3. Однако критической точкой функции будет только х3 = 3, так как первая х=-2 не принадлежит области определения функции. Критическая точка x2 = 3 разбивает область определения функции на два интервала (1; 3) и (3; + ∞), на каждом из которых производная сохраняет свой знак. Так как у' (2) =—4<0 и у'(4) = 2>0, то производная отрицательна на (1; 3) и положительна на [3; + оо]. Следовательно, функция убывает на интервале (1; 3) и возрастает на (3; + ∞) (рис.1).
имеет два корня x1= -2 и х2= 3. Однако критической точкой функции будет только х3 = 3, так как первая х=-2 не принадлежит области определения функции. Критическая точка x2 = 3 разбивает область определения функции на два интервала (1; 3) и (3; + ∞), на каждом из которых производная сохраняет свой знак. Так как у' (2) =—4<0 и у'(4) = 2>0, то производная отрицательна на (1; 3) и положительна на [3; + оо]. Следовательно, функция убывает на интервале (1; 3) и возрастает на (3; + ∞) (рис.1).

Рис.1
Точка х0 называется точкой максимума (минимума) функции у = f(х), если для всех х≠х0 из некоторой окрестности этой точки выполняется неравенство f(x)<f(x0) (f(x)>f(x0)).
Точки максимума и минимума называются точками экстремума.
Для нахождения точек экстремума функции нужно:
1. Найти производную и критические точки функции.
2. Исследовать знак производной в некоторой окрестности каждой критической точки.
Если функция непрерывна в критической точке х0, аее производная меняет знак при переходе через х0, то х0 — точка экстремума функции. При этом х0 — точка максимума, если знак меняется с плюса на минус, и минимума, если знак меняется с минуса на плюс. Если же знак производной сохраняется при переходе через рассматриваемую точку, то функция не имеет экстремума в этой точке.
|
|
|
Иногда для нахождения точек экстремума удобно пользоваться следующим правилом.
Если в некоторой точке х0 первая производная функции у = f(x) равна нулю 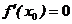 , а вторая производная отлична от нуля, то в этой точке функция имеет экстремум, а именно: максимум, если f" (х0) < 0, и минимум, если f" (х0) >0.
, а вторая производная отлична от нуля, то в этой точке функция имеет экстремум, а именно: максимум, если f" (х0) < 0, и минимум, если f" (х0) >0.
Пример 2.2. Найти точки экстремума функции у= x(x+1)3 .
Решение. Способ 1. Функция определена и дифференцируема на (-∞; +∞). Найдем ее производную: у' = (х + 1)2(4х+1). Производная равна нулю в точках х = —1 и х = -1/4, т. е. это критические точки функции. Проверим, меняет ли производная знак при переходе через эти точки. На интервалах (-∞; -1) и (-1; -1/4) производная отрицательна, а на (-1/4; + ∞) — положительна. Следовательно, х = —1/4—точка минимума, а в точке х=—1 экстремума нет (рис.2).
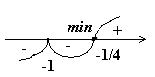
Рис.2
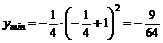 .
.
Способ 2. Найдем вторую производную: у" = 6(х+1)(2х+1).Так как у"(—1/4)=9/4 > 0, то х = —1/4— точка минимума; у" (—1) = 0, поэтому с помощью второй производной установить наличие экстремума в точке х=0 невозможно.
|
|
|
Выпуклость графика функции. Точки перегиба
График дифференцируемой функции называется выпуклым вверх, (вниз) на некотором интервале, если в пределах указанного интервала он лежит не выше (не ниже) любой своей касательной.
Если в рассматриваемом интервале вторая производная положительна, то на этом интервале график функции выпукл вниз (рис.4), если же вторая производная отрицательна, то выпукл вверх (рис.3).
Для нахождения интервалов выпуклости графика функции нужно:
1. Найти область определения функции, если она не указана.
2. Найти вторую производную функции и точки, в которых она равна нулю или не существует.
3. Установить знак второй производной в каждом из интервалов, на которые разбивается область определения функции найденными точками.
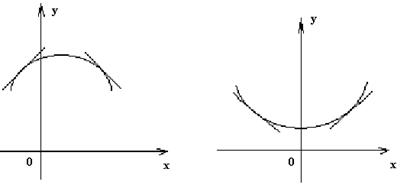
Рис.3 Рис.4
Пусть функция у=f(х) непрерывна в точке х0. Точка (х0 ;f(х0)) называется точкой перегиба графика функции, если при переходе через нее кривая меняет направление выпуклости.
Если функция непрерывна в точке х0, а ее вторая производная меняет знак при переходе через эту точку, то х0 является абсциссой точки перегиба графика данной функции.
Для нахождения точек перегиба графика нужно:
1. Найти все точки из области определения функции, в которых вторая производная обращается в нуль, или не существует.
2. Исследовать знак второй производной в некоторой окрестности каждой из этих точек.
Пример 3.1. Найти интервалы выпуклости и точки перегиба графика функции у = х4 — 6х2+5.
Решение. Функция y определена при  . Находим первую и вторую производные функции:
. Находим первую и вторую производные функции: 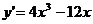 ,
, 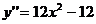
Вторая производная всюду существует и обращается в нуль в точках х = 1, х = -1. Область определения функции разбивается этими точками на три интервала: (-∞ ;-1) и (-1;1) (1,+ ∞ ) в каждом из которых вторая производная сохраняет свой знак: f"(x)>0 при |х|>1, f"(x)<0 при |х|<1 (рис.5).

Рис.5
Следовательно, на интервалах (- ∞; - 1) и (1;+∞)график функции выпуклый вниз, а на интервале (- 1; 1) — выпуклый вверх. Точки x = - 1 и x=1 - точки перегиба графика.
Асимптоты
Асимптоты графика функции подразделяются на вертикальные и наклонные. Вертикальной асимптотой графика функции y=f(x) называется прямая х=х0, если хотя бы один из пределов f(х0-0) или f(х0+0) равен символу +∞ или -∞, 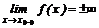 . Ясно, что вертикальными асимптотами являются прямые х=х0, если х0 – точка бесконечного разрыва функции f(х).
. Ясно, что вертикальными асимптотами являются прямые х=х0, если х0 – точка бесконечного разрыва функции f(х).
Наклонной асимптотой графика функции у=f(х) при х → + ∞ (х → - ∞) называется прямая у=kx+b, если:
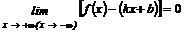 . (1)
. (1)
Для того чтобы график функции y=f(x) имел наклонную асимптоту при х→+∞ (х→-∞), необходимо и достаточно, чтобы существовали два конечных предельных значения:

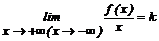 (2)
(2)
Тогда уравнение асимптоты есть у=kx+b.
Определением наклонных асимптот сразу же решается вопрос о поведении функции на бесконечности. Соотношение (1) показывает, что график функции y=f(x) при х→+∞ (х→-∞) становится сколь угодно близким к графику прямой у=kx+b. Отметим, что пределы (2), а следовательно и асимптоты графика функции, при х→+∞ и х→-∞ могут не совпадать.
Проверить наличие асимптот графиков функций:
1)  ; 2)
; 2) 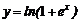 .
.
Пример 4.1. Функция  определена при -∞<х<+∞, х
определена при -∞<х<+∞, х 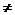 0.
0.
Вычисляя пределы: 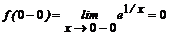 ;
;
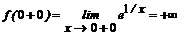 ,
,
видим, что точка х=0 является точкой бесконечного разрыва, а прямая х=0 – вертикальной асимптотой функции при х→0+0.
Для определения наклонной асимптоты вычислим пределы (2):
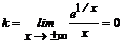 ;
; 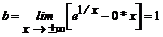 .
.
Отсюда получаем уравнение асимптоты у=1 при x→±∞.
Пример 4.2. Функция 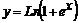 определена при -∞<x<+∞ и, следовательно, не имеет вертикальных асимптот. Вычисляя пределы (2), получаем:
определена при -∞<x<+∞ и, следовательно, не имеет вертикальных асимптот. Вычисляя пределы (2), получаем:
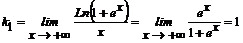
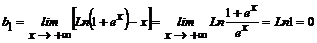 ;
;
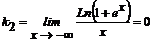 ;
; 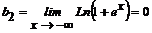 .
.
Отсюда график функции имеет наклонные асимптоты y=kx+b; при x→+∞ y=x и при x→ - ∞ y=0 .
5. Построение графиков функций
Исследование функций и построение ее графика целесообразно проводить по следующей схеме:
1. Найти область определения функции, если она не указана.
2. Выяснить, будет ли функция четной или нечетной.
3. Выяснить, будет ли функция периодической.
4. Найти, если это позволяет область определения, предел функции на бесконечности.
5. Исследовать функцию на непрерывность; изучить поведение функции в окрестности точек разрыва, если они существуют.
6. Найти интервалы возрастания и убывания функции, ее точки экстремума; вычислить значение функции в точках максимума и минимума.
7. Найти точки пересечения графика функции с осями координат (если это не приводит к уравнениям, методы решения которых неизвестны).
8. Найти промежутки выпуклости вверх (вниз) и точки перегиба графика функции.
9. Проверить наличие асимптот.
Пример 5.1. Построить график функции f(х) =16x( x+1)3
Решение.
1. Функция определена на (—∞; + ∞).
2. Она не является ни четной, ни нечетной f(-x)=16(-x)(-x+1)3 ≠ f(x), f(-x) ≠ -f(x).
3. Функция непериодическая, так как является многочленном.
4. При х →±∞ 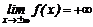 у = f(х) принимает как угодно большие по модулю значения.
у = f(х) принимает как угодно большие по модулю значения.
5. Функция непрерывна в области определения, как многочлен.
6. Найдем ее производную f’ (х) = 16(х + 1)2(4x+1).
Критические точки функции х1=-1, х2 = -1/4. Функция убывает на интервале [-¥; -1/4) и возрастает на (-1/4; + ∞). Точка x=-1/4 - ее точка минимума. Значение функции в точке минимума равно f(-1/4) = -27/16.
7. Точки пересечения с осями координат (0; 0); (-1; 0).
8. С помощью второй производной определим f" (х) = 96 (x+1)(2х+1). Она обращается в нуль в точках x1= -1,x2= -1/2. На интервалах [- ∞;-1] и [-1/2; + ∞)график функции выпуклый вниз, на интервале [- 1; -1/2] -выпуклый вверх, так как  , точки (-1; 0), (-1/2;-1)—точки перегиба графика функции.
, точки (-1; 0), (-1/2;-1)—точки перегиба графика функции.
9. Асимптот нет, так как функция - многочлен.
Используя полученные результаты, строим график функции (рис.6).
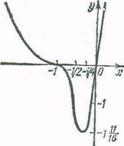
Рис.6
Пример 5.2. Построить график функции f (х) =x2/(x2-1).
Решение. 1. Область определения функции — вся числовая прямая, кроме x1 = -1, x2 = 1.
2. Функция четная, так как f(—х)=f(х). Следовательно, график функции симметричен oтносительно оси ординат. Поэтому для построения графика достаточно исследовать функцию на [0; 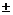 ¥].
¥].
3. Функция непериодическая.
4. 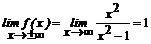
5. Функция непрерывна в своей области определения. Точки х1 = -1, x2=1 — ее точки разрыва. При х→1 функция принимает сколь угодно большие по модулю значения, причем справа от точки х = 1 — положительные, слева—отрицательные.
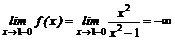
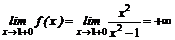 ;
;
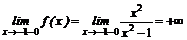
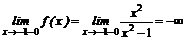 .
.
6. Найдем производную: f'(x)= -2x/(x2-1)2. Так как на (0; 1) и (1; + ∞) производная отрицательна, то функция убывает на этих интервалах.
7. Точки пересечения с осями координат (0,0).
8. Находим вторую производную функции  .
.
точек перегиба нет, так как уравнение 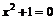 не имеет решений, но в интервале (-¥;-1) и (1;+¥)
не имеет решений, но в интервале (-¥;-1) и (1;+¥)  график выпуклый вниз, а в интервале
график выпуклый вниз, а в интервале
(-1;1) 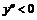 график функции выпуклый вверх.
график функции выпуклый вверх.
9) x=1, x=-1 – вертикальные асимптоты(см. п.5). Проверим наличие наклонных асимптот 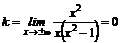 ,
, 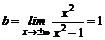 , значит y=1 – горизонтальная асимптота.
, значит y=1 – горизонтальная асимптота.
Используя полученные результаты, строим график функции (рис. 7).

Рис.7
Пример 5.3. Построить график функции 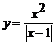
 .
.
Решение. 1. Функция определена при всех значениях х, кроме х= 1, т. е.
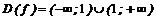
Функция может принимать все неотрицательные значения, т. е.
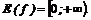
2. Функция не является четной и не является нечетной.
3. Функция не является периодической.
4. 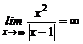 .
.
5. Функция имеет бесконечный разрыв в точке х=1, поскольку
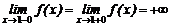 .
.
Прямая х = 1 является вертикальной асимптотой графика функции.
6. Для исследования данной функции на монотонность и для нахождении ее экстремумов вычислим производную функции.
Поскольку выражение данной функции содержит модуль, то ее производная будет задаваться двумя разными выражениями на интервалах
(-¥; 1) и (1; +∞) на которых модуль раскрывается по-разному, а именно:

Функция имеет две критические точки, х=0 и х=2, в которых производная равна нулю, а при х = 1 производная не существует. Заметим, что точка х = 1 не является критической точкой функции, так как функция не определена в этой точке.
Знаки производной 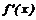 показаны на рис.8.
показаны на рис.8.
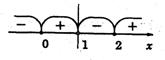
Рис.8
Исследование знака производной позволяет заключить, что:
1) на промежутке х Î(-∞,0] функция убывает;
2) на промежутке х Î [0,1) функция возрастает;
3) на промежутке х Î (1, 2] функция убывает;
4) на промежутке х Î [2;+∞) функция возрастает.
В точке х = 0 функция имеет минимум, ƒ (0) = 0. В точке х = 2 функция также имеет минимум, ƒ (2) = 4 Функция не имеет максимумов.
7. График функции имеет единственную общую точку с осями координат — точку (0;0). 8. 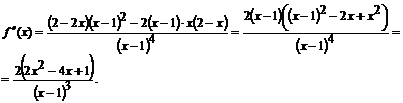
Точек перегиба нет, так как  при
при 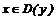 , график всюду выпуклый вниз.
, график всюду выпуклый вниз.
9. Кроме того, график функции имеет наклонные асимптоты. Поскольку при х→+∞ выполнено:
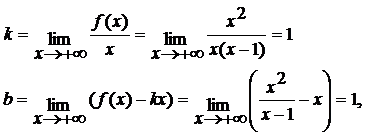
то прямая у = х + 1 является наклонной асимптотой при х→+∞.
Далее, при х→+∞ выполнено:
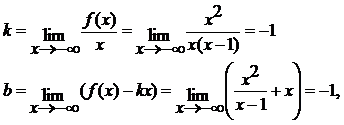
поэтому прямая у = -х-1 является наклонной асимптотой графика функции при х→-∞.
График функции представлен на рис. 9.

Рис.9
Варианты заданий
Задание 1.
Провести полное исследование функций и построить их графики
1. 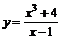
| 2. 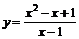
|
3. 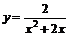
| 4. 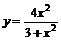
|
5. 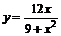
| 6. 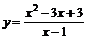
|
7. 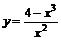
| 8. 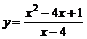
|
9. 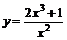
| 10. 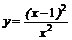
|
11. 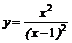
| 12. 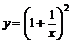
|
13. 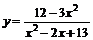
| 14. 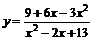
|
15. 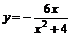
| 16. 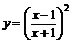
|
17. 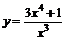
| 18. 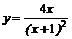
|
19. 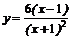
| 20. 
|
21. 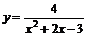
| 22. 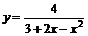
|
23. 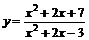
| 24. 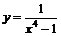
|
25. 
| 26. 
|
27. 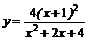
| 28. 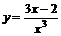
|
29. 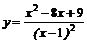
| 30. 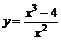
|
Задание 2.
Провести полное исследование функций и построить их графики
1. 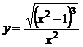
| 2. 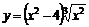
|
3. 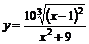
| 4. 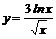
|
5. 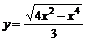
| 6. 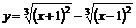
|
7. 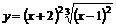
| 8. 
|
9. 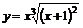
| 10. 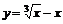
|
11. 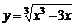
| 12. 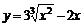
|
13. 
| 14. 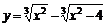
|
15. 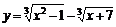
| 16. 
|
17. 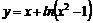
| 18. 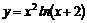
|
19. 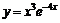
| 20. 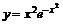
|
21. 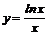
| 22. 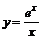
|
23. 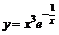
| 24. 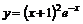
|
25. 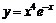
| 26. 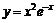
|
27. 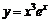
| 28. 
|
29. 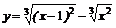
| 30. 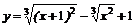
|
Список литературы
1. Берман Г. Н. Сборник задач по курсу математического анализа. – М.: Наука, 1981.
2. Бугров Я. С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1980.
3. Данко П. Е., Попов А. Г., Кожевников Т. Я. Высшая математика в упражнениях и задачах. – М.: Высш. математика, 1986.
4. Пискунов Н. С. Дифференциальное и интегральное исчисление. – М.: Наука, 1984.
Содержание
1. Понятие числовой функции, ее простейшие свойства 1
2. Возрастание и убывание функции. Точки экстремума 1
3. Выпуклость графика функции. Точки перегиба 4
4. Асимптоты 5
5. Построение графиков функций 6
6. Варианты заданий 12
Список литературы 13
Редактор Л.А.Матвеева
Подписано в печать 16.09.04 . Бумага офсетная. Формат 60х84 1/16.
Гарнитура “Таймс”. Печать трафаретная. Усл.-печ.л. 1,1 . Уч.-изд.л. 0,9
Тираж 100 экз. Заказ №
Издательство Уфимского государственного нефтяного технического университета
Адрес издательства:
450062, РБ, г.Уфа, ул.Космонавтов, 1.
Дата добавления: 2018-04-05; просмотров: 285; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
