Перечень ресурсов информационно-коммуникационной сети «Интернет»
Nbsp; Математика Методические указания к контрольной работе для студентов I курса Составитель: канд. пед. наук, доцент Л. М. Троицкая Методические указания предназначены студентам–заочникам для помощи при выполнении контрольных заданий по дисциплине Математика. Они содержат примеры решения типовых задач, аналогичные заданиям из контрольной работы. При решении задач необходимо использовать учебно-методическую литературу, рекомендуемую рабочей программой дисциплины.
Правила выполнения и оформления контрольных работ
1. Контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами синего, черного или фиолетового цвета. Необходимо оставлять поля шириной 4 – 5 см для замечаний рецензента.
2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, название дисциплины; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента. В конце работы следует поставить дату и расписаться. Студент выполняет те задачи, последняя цифра которых совпадает с последней цифрой его учебного шифра. Например, студент, учебный шифр которого имеет последнюю цифру 0, в контрольной работе решает задачи 10, 20, 30, 40, 50, 60.
3. В работу должны быть включены все задачи, указанные в задании строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не засчитываются.
|
|
|
4. Решения задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. Оформление решения каждой задачи начинается с новой страницы.
5. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
7. После получения прорецензированной работы, как зачтенной, так и незачтенной, студент должен исправить все, отмеченные рецензентом, ошибки и недочеты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
|
|
|
При высылаемых исправлениях должна обязательно находиться прорецензированная работа. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
§1. Теоретические сведения и типовое решение задач
Задача 1
Даны вершины пирамиды 
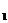 (
( 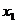 ,
, 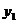 ,
, 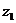 ),
), 
 (
(  ,
, 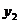 ,
, 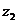 ),
), 
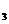 (
( 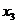 ,
, 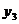 ,
,  ),
), 
 (
(  ,
, 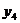 ,
, 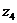 ).
).
Найти:
1. Длину ребра 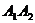 .
.
2. Угол между ребрами 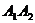 и
и 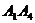 .
.
3. Уравнение грани 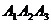 и её площадь.
и её площадь.
4. Уравнения высоты, опущенной из вершины 
 на грань
на грань 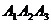 .
.
Например: 
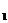 (3;7;10),
(3;7;10), 
 (-2;-5;1),
(-2;-5;1), 
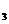 (6;5;1),
(6;5;1), 
 (-4;6;-2).
(-4;6;-2).
Решение
Предварительно сделаем рисунок пирамиды:
– зафиксируем трехмерное геометрическое пространство с помощью декартовой прямоугольной системы координат и точками отметим вершины пирамиды по их координатам;
– соединим вершины пирамиды отрезками прямых;
– введем в рассмотрение векторы  выбирая вершину
выбирая вершину 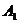 в качестве их общего начала (рис.1).
в качестве их общего начала (рис.1).

Рис.1
1. Длину ребра 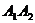 находим по формуле длины вектора
находим по формуле длины вектора 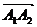 , как расстояния между точками
, как расстояния между точками 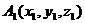 и
и 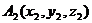 в декартовой прямоугольной системе координат
в декартовой прямоугольной системе координат
|
|
|

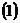
2. Для нахождения угла между ребрами 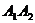 и
и 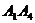 используем формулу скалярного произведения векторов
используем формулу скалярного произведения векторов 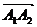 и
и  , выраженного через координаты перемножаемых сомножителей.
, выраженного через координаты перемножаемых сомножителей.
Обозначим 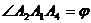 .
.
По определению скалярного произведения:
 .
. 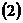
Тогда
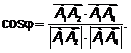 .
. 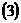
Скалярное произведение  есть сумма произведений одноименных координат перемножаемых векторов:
есть сумма произведений одноименных координат перемножаемых векторов:
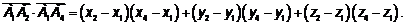 .
. 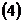
Подставляя в 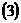 длины векторов
длины векторов 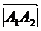 и
и 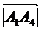 и скалярное произведение
и скалярное произведение 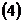 , получим:
, получим:
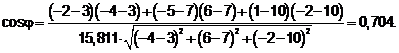
Таким образом: 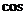
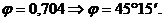
Угол  находим по таблице значений
находим по таблице значений 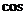
 по правилу:
по правилу:
+ 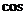

 ,
,
– 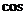

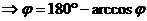 .
.
Рекомендуется использовать таблицы ″Брадис В.М. Четырехзначные математические таблицы. – М.: Дрофа, 2004″ или калькулятор.
3. Для составления уравнения грани 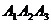 используем определение понятия "плоскость" и геометрический смысл смешанного произведения трех векторов.
используем определение понятия "плоскость" и геометрический смысл смешанного произведения трех векторов.
Из школьного курса математики известно, что плоскость однозначно определена, если заданы её три любые точки. Отсюда следует, что плоскость можно определить с помощью двух векторов, расположенных в плоскости и имеющих общее начало.
|
|
|
Векторы  и
и  имеют общее начало точку
имеют общее начало точку 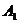 , называемую начальной точкой плоскости. Векторы
, называемую начальной точкой плоскости. Векторы 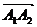 и
и  называются направляющими векторами плоскости. Мысленно проведем ещё один вектор
называются направляющими векторами плоскости. Мысленно проведем ещё один вектор 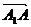 , конец которого точка А является произвольной точкой плоскости. Векторы, располагаемые в одной плоскости, называются компланарными. В соответствии с геометрическим смыслом величина смешанного произведения трех векторов
, конец которого точка А является произвольной точкой плоскости. Векторы, располагаемые в одной плоскости, называются компланарными. В соответствии с геометрическим смыслом величина смешанного произведения трех векторов  выражает объем параллелепипеда, построенного на этих векторах как на сторонах. Очевидно, что если векторы располагаются в одной плоскости, то объем равен нулю. Таким образом, приравнивая смешенное произведение нулю, получим условие компланарности трех векторов. Учитывая также, что точка
выражает объем параллелепипеда, построенного на этих векторах как на сторонах. Очевидно, что если векторы располагаются в одной плоскости, то объем равен нулю. Таким образом, приравнивая смешенное произведение нулю, получим условие компланарности трех векторов. Учитывая также, что точка  является произвольной точкой плоскости, это условие рассматривается в качестве уравнения плоскости:
является произвольной точкой плоскости, это условие рассматривается в качестве уравнения плоскости:
 = 0
= 0 
Выражение  определяет плоскость двумя способами:
определяет плоскость двумя способами:
1) тремя точками 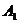 ,
, 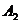 ,
, 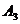 ,
,
2) начальной точной 
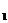 и двумя направляющими векторами
и двумя направляющими векторами  и
и  .
.
Во втором случае присутствует идея зафиксировать множество точек плоскости посредством системы координат.
Смешанное произведение трех векторов находится через координаты перемножаемых сомножителей с помощью определителя 3-го порядка, каждая строка которого состоит из координат соответствующего вектора, поэтому 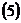 примет вид:
примет вид:
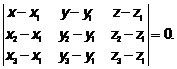 .
. 
Раскроем определитель  по элементам 1-ой строки:
по элементам 1-ой строки:
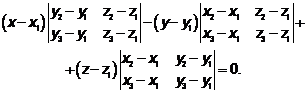 .
.
Обозначим:
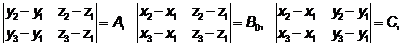
тогда
 .
.
Пусть 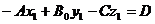 ,
,  ,
,
тогда
 .
. 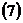

Уравнение 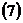 называется уравнением плоскости, проходящей через три заданные точки
называется уравнением плоскости, проходящей через три заданные точки 
 ,
, 


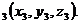 Коэффициенты
Коэффициенты 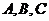 по своему смыслу суть координаты вектора, нормального к плоскости.
по своему смыслу суть координаты вектора, нормального к плоскости.
Для числовых данных примера имеем:
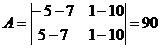
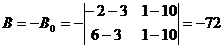
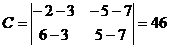
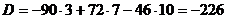
Уравнение грани 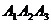 принимает вид:
принимает вид:
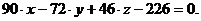

Любая точка этой грани с координатами 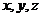 должна удовлетворять уравнению
должна удовлетворять уравнению 
Для нахождения площади грани 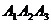 воспользуемся геометрическим смыслом модуля векторного произведения
воспользуемся геометрическим смыслом модуля векторного произведения 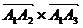 , равного площади параллелограмма, построенного на векторах
, равного площади параллелограмма, построенного на векторах 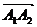 и
и  , как на сторонах
, как на сторонах
Имеем:
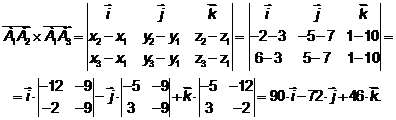
Координаты полученного вектора, который по определению векторного произведения 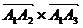 является нормальным к плоскости перемножаемых векторов, совпали с коэффициентами уравнения грани
является нормальным к плоскости перемножаемых векторов, совпали с коэффициентами уравнения грани 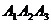 , что подтверждает правильность выполненных расчетов.
, что подтверждает правильность выполненных расчетов.
Площадь грани 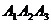 равна:
равна:

4. Чтобы найти уравнения высоты, опущенной из вершины 
 на грань
на грань 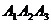 , предварительно составим уравнения прямой в пространстве.
, предварительно составим уравнения прямой в пространстве.
Прямая линия в пространстве, как и на плоскости, однозначно определена, если известны координаты любой одной точки, принадлежащей прямой, а также задан вектор, параллельный прямой. При этом точка называется начальной точкой, а вектор – направляющим вектором прямой.
В качестве начальной точки рассматривается точка  , направляющий вектор представлен вектором
, направляющий вектор представлен вектором 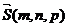 .Возьмем на прямой произвольную точку
.Возьмем на прямой произвольную точку 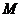 (
( 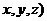 и проведем вектор
и проведем вектор 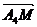 . Поскольку векторы
. Поскольку векторы  и
и 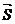 коллинеарны, то
коллинеарны, то
 =
= 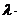
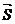 ,
, 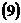
где 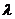 – некоторое действительное число (параметр).
– некоторое действительное число (параметр).
Отсюда
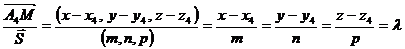 .
. 
Уравнения  называются каноническими уравнениями прямой в пространстве.
называются каноническими уравнениями прямой в пространстве.
Если вектор 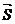 лежит на прямой и задан координатами точек его начала и конца, например, точками
лежит на прямой и задан координатами точек его начала и конца, например, точками 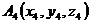 и
и 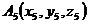 , то
, то  можно записать в виде уравнений прямой, проходящей через две заданные точки:
можно записать в виде уравнений прямой, проходящей через две заданные точки:
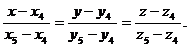
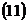
Уравнения высоты, опущенной из вершины 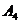 на грань
на грань 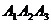 , ищем в виде
, ищем в виде  , где в качестве направляющего вектора возьмем вектор, нормальный к грани
, где в качестве направляющего вектора возьмем вектор, нормальный к грани 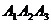 . Таким вектором является вектор, равный векторному произведению векторов
. Таким вектором является вектор, равный векторному произведению векторов 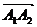 и
и  . Его координаты получим, вычисляя векторное произведение
. Его координаты получим, вычисляя векторное произведение 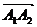

 через координаты перемножаемых векторов, или непосредственно из выражения уравнения плоскости
через координаты перемножаемых векторов, или непосредственно из выражения уравнения плоскости  .
.
Для данных числового примера уравнения высоты, опущенной из вершины 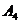 на грани
на грани 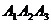 , имеют вид
, имеют вид
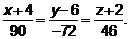 .
. 
Определим длину высоты, используя 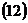 :
:
– запишем уравнение высоты в параметрическом виде
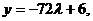
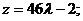
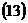
– подставим 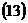 в уравнение
в уравнение  грани
грани 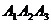

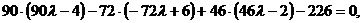
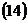
– из 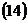 находим
находим  ,
,
– обозначим точку пересечения высоты с гранью 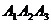 через
через 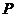 , подставим
, подставим 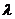 в уравнения высоты
в уравнения высоты 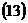 , найдем координаты точки
, найдем координаты точки 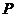
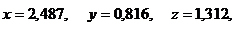
– определяем длину высоты по формуле 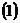 :
:
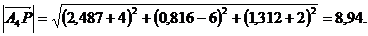

Ответ:
1. Длина ребра 

2. Угол между ребрами 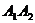 и
и 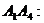
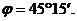
3. Уравнение грани 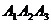 :
: 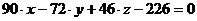 ; площадь грани
; площадь грани 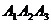 :
: 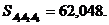
4. Уравнения высоты, опущенной из вершины 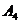 на грань
на грань 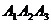 :
: 
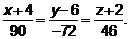 .
.
Задача 2
Составить уравнение множества точек, для каждой из которых выполняется следующее условие:
1. Сумма квадратов расстояний до точек 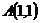 и
и  равна 20.
равна 20.
2. Сумма квадратов расстояний до точек 
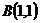 и
и 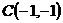 равна 28.
равна 28.
3. Сумма квадратов расстояний до точек 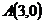 ,
, 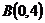 ,
, 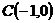 и
и  равна 58.
равна 58.
4. Квадрат расстояния до точки  на 3 больше квадрата расстояния до оси абсцисс.
на 3 больше квадрата расстояния до оси абсцисс.
5. Сумма расстояний до точек 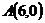 и
и 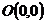 равна 10.
равна 10.
6. Квадрат расстояния до точки 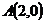 на 16 больше квадрата расстояния до оси ординат.
на 16 больше квадрата расстояния до оси ординат.
7. Сумма квадратов расстояний до сторон прямоугольника, образованного прямыми 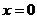 ,
,  ,
, 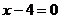 ,
, 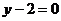 , равна 20.
, равна 20.
8. Расстояние до точки  равно расстоянию до оси абсцисс.
равно расстоянию до оси абсцисс.
9. Разность расстояний до точек  и
и  равна 8.
равна 8.
10. Расстояние до точки 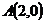 равно расстоянию до оси ординат.
равно расстоянию до оси ординат.
Решение
Линии на плоскости, определяемые алгебраическими уравнениями второй степени относительно координат их точек вида
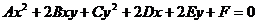 ,
, 
называются кривыми линиями второго порядка, а уравнения  – общими уравнениями этих линий. Коэффициенты
– общими уравнениями этих линий. Коэффициенты  – действительные числа.
– действительные числа.
В задаче 2 изучаются кривые линии второго порядка: окружность, эллипс, гипербола, парабола.
Каждая линия образуется в соответствии с её определяющим свойством. Логика вывода уравнения линии строится на основе этого свойства.
Окружность: множество точек плоскости, каждая из которых равноудалена от точки плоскости, называемой центром окружности (рис.2).

Рис.2
Основное свойство окружности:
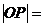 r.
r. 
Уравнение окружности:
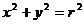 ,
, 
где r – радиус.
Если центр окружности 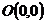 перемещается в положение точки
перемещается в положение точки 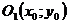 и располагается в первом квадранте, то уравнение окружности
и располагается в первом квадранте, то уравнение окружности 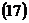 примет вид:
примет вид:
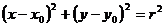 .
. 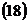
В 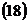 координата центра окружности, как по оси абсцисс, так и по оси ординат, входит с противоположным знаком. Если, например, в уравнении
координата центра окружности, как по оси абсцисс, так и по оси ординат, входит с противоположным знаком. Если, например, в уравнении 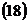 имеем
имеем 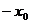 и
и 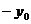 , то центр окружности находится в точке
, то центр окружности находится в точке 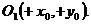
Задание уравнения  позволяет по его виду установить координаты центра окружности и, зная радиус, построить окружность.
позволяет по его виду установить координаты центра окружности и, зная радиус, построить окружность.
Эллипс: множество точек плоскости, каждая из которых удалена от двух точек плоскости, называемых фокусами эллипса, на равную сумму расстояний (рис.3).
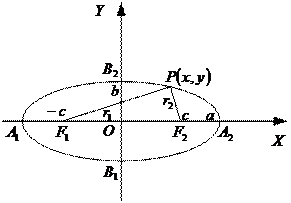
Рис.3
На рис.3:
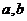 – длины большой и малой полуосей,
– длины большой и малой полуосей,
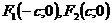 – фокусы эллипса, с – расстояние от центра до фокуса,
– фокусы эллипса, с – расстояние от центра до фокуса,
r 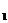 , r
, r  – фокальные радиусы точки
– фокальные радиусы точки 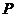
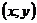 ,
,
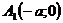 ,
,  ,
, 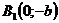 ,
, 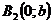 – вершины.
– вершины.
Основное свойство эллипса:
 .
. 
Уравнение эллипса:
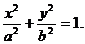
Имеет место соотношение: 
Если центр эллипса  перемещается в положение
перемещается в положение  , то уравнение
, то уравнение 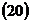 принимает вид:
принимает вид:
 .
. 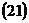
Гипербола: множество точек плоскости, каждая из которых удалена от двух точек плоскости, называемых фокусами гиперболы, на равную по абсолютной величине разность расстояний (рис.4).
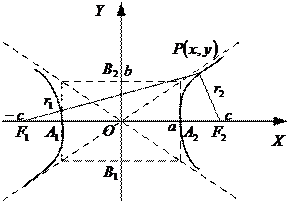
Рис.4
На рис.4:
 – длина действительной полуоси,
– длина действительной полуоси,
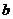 – длина мнимой полуоси,
– длина мнимой полуоси,
 ,
, 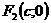 – фокусы гиперболы,
– фокусы гиперболы,
 – расстояние от центра до фокуса;
– расстояние от центра до фокуса;
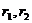 – фокальные радиусы точки
– фокальные радиусы точки 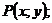
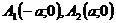 – действительные вершины,
– действительные вершины,
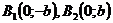 – мнимые вершины,
– мнимые вершины,
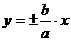 – асимптоты.
– асимптоты.
Основное свойство гиперболы:
 .
. 
Уравнение гиперболы:
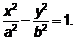
Имеет место соотношение: 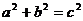 .
.
При перемещении центра гиперболы  в положение точки
в положение точки  уравнение
уравнение  принимает вид:
принимает вид:
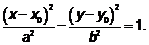
Парабола: множество точек плоскости, каждая из которых удалена от точки плоскости, называемой фокусом параболы, на расстояние, равное расстоянию удаления от прямой, называемой директрисой параболы (рис.5).
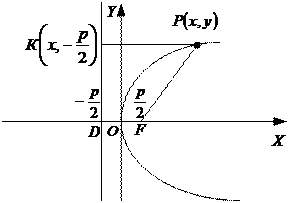
Рис.5
На рис.5:
 – вершина параболы,
– вершина параболы,
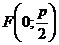 – фокус,
– фокус,
 – уравнение директрисы,
– уравнение директрисы,
Основное свойство параболы:
 .
. 
Уравнение параболы:
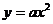 ,
, 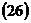
где  ,
,  – параметр параболы.
– параметр параболы.
Если вершину параболы переместить в точку 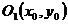 , то уравнение
, то уравнение 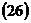 принимает вид:
принимает вид:
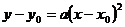 .
. 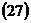
Поменяв переменные 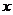 и
и  местами, получим уравнение:
местами, получим уравнение:
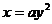 или
или 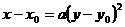
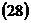
с осью 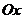 в качестве оси симметрии.
в качестве оси симметрии.
Уравнения  ,
,  ,
,  ,
, 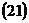 ,
, 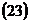 ,
, 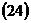 ,
, 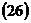 ,
, 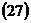 называются каноническими, т.е. простейшими. Вид уравнений содержит всю необходимую информацию для построения кривой линии.
называются каноническими, т.е. простейшими. Вид уравнений содержит всю необходимую информацию для построения кривой линии.
Уравнение  при
при  =0
=0


называется общим уравнением окружности, эллипса, гиперболы, параболы.
Утверждение: уравнение  определяет окружность при
определяет окружность при 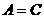 , эллипс при
, эллипс при 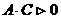 , гиперболу при
, гиперболу при 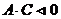 , параболу при
, параболу при  .
.
Перейдем от уравнения  к каноническому виду уравнений окружности
к каноническому виду уравнений окружности  , эллипса
, эллипса  , гиперболы
, гиперболы 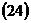 , параболы
, параболы 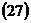 .
.
Преобразование  к виду уравнения окружности
к виду уравнения окружности 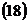
Пусть 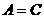 . Из
. Из  получим:
получим:
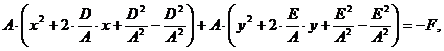
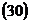
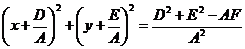 .
.
Здесь: координаты центра окружности 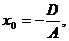
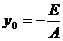 ,
, 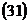
Радиус окружности 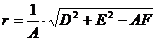 .
. 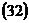
Пример 1. Составить уравнение множества точек, для каждой из которых сумма квадратов расстояний до точек 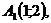

 равна
равна 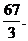
Решение
1. Обозначим произвольную точку искомого множества точек через 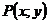 и запишем её заданное свойство
и запишем её заданное свойство
 .
.
Или 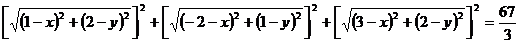 .
.
2. Приведем это выражение к виду  :
:
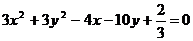 .
. 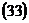
Уравнение 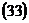 соответствует виду
соответствует виду  при
при 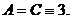 Следовательно,
Следовательно, 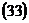 является общим уравнением окружности, представляющим заданное множество точек,
является общим уравнением окружности, представляющим заданное множество точек, 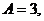
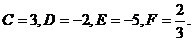
3. По формулам 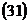 и
и 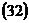 находим координаты центра окружности и радиус:
находим координаты центра окружности и радиус:
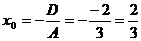 ,
,
 ,
,
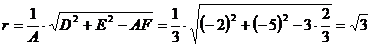 .
.
4. По выражению 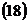 составим каноническое уравнение окружности, представляющее заданное множество точек:
составим каноническое уравнение окружности, представляющее заданное множество точек:
 .
. 
Выражение  можно получить также непосредственным преобразованием
можно получить также непосредственным преобразованием 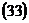 в соответствии с порядком вывода уравнения
в соответствии с порядком вывода уравнения 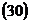 .
.
Преобразование  к виду уравнения эллипса
к виду уравнения эллипса 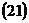
Пусть  ,
, 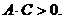
Получим 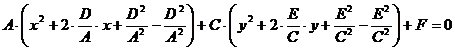 ,
,
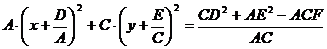 ,
,
 .
. 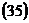
Здесь: координаты центра эллипса
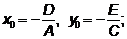
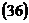
большая полуось  ,
, 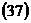
малая полуось 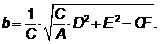 .
. 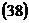
Пример 2. Составить уравнение множества точек для каждой из которых сумма расстояний до точек 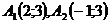 равна 5.
равна 5.
Решение
1. Пусть 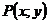 – произвольная точка заданного множества точек. Запишем её заданное свойство
– произвольная точка заданного множества точек. Запишем её заданное свойство
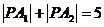 .
.
Или 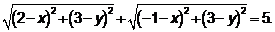 .
.
2. Приведем это выражение к виду  :
:
 .
. 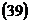
Уравнение 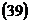 соответствует виду
соответствует виду  при
при  ,
, 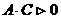 .
.
Следовательно, 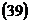 является общим уравнением эллипса, представляющим заданное множество точек,
является общим уравнением эллипса, представляющим заданное множество точек, 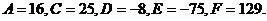
3. По формулам 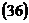 ,
, 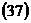 ,
, 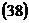 находим координаты центра эллипса, большую и малую полуоси.
находим координаты центра эллипса, большую и малую полуоси.
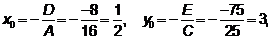
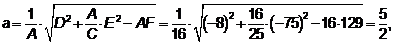 ,
,
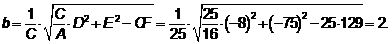 .
.
4. По выражению 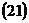 составим каноническое уравнение эллипса
составим каноническое уравнение эллипса

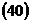
Уравнение 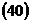 можно получить также преобразованием выражения
можно получить также преобразованием выражения 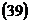 в соответствии с порядком вывода уравнения
в соответствии с порядком вывода уравнения 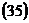 .
.
Преобразование  к виду уравнения гиперболы
к виду уравнения гиперболы 
Порядок вывода уравнения гиперболы 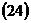 и его вид не отличаются от порядка вывода и вида уравнения эллипса
и его вид не отличаются от порядка вывода и вида уравнения эллипса 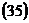 с учетом замечания: поскольку для эллипса имеет место
с учетом замечания: поскольку для эллипса имеет место 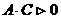 , а для гиперболы
, а для гиперболы 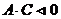 , то уравнение
, то уравнение 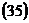 в форме
в форме 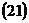 отличается от уравнения гиперболы в форме
отличается от уравнения гиперболы в форме 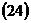 знаком в левой части перед вторым слагаемым (см.
знаком в левой части перед вторым слагаемым (см. 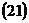 и
и 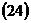 ).
).
Уравнение 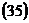 используется в качестве уравнения гиперболы, при этом необходимо иметь ввиду, что
используется в качестве уравнения гиперболы, при этом необходимо иметь ввиду, что
координаты центра гиперболы
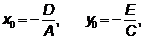

действительная полуось
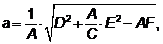 ,
, 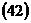
мнимая полуось
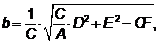 ,
, 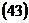
где  ,
, 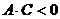 .
.
Пример 3. Составить уравнение множества точек, для каждой из которых разность расстояний до точек 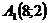 и
и  равна 8.
равна 8.
Решение
1. Пусть 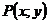 – произвольная точка заданного множества точек. По условию имеем
– произвольная точка заданного множества точек. По условию имеем
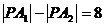 .
.
Или  .
. 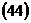
2. Приведем это выражение к виду  , получим
, получим
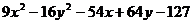 ,
,
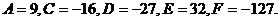
В уравнении 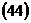
 ,
, 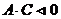 , что соответствует условию описания гиперболы и представления таким образом заданного множества точек.
, что соответствует условию описания гиперболы и представления таким образом заданного множества точек.
3. По формулам  ,
, 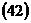 ,
, 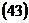 находим координаты центра гиперболы, действительную и мнимую полуоси
находим координаты центра гиперболы, действительную и мнимую полуоси
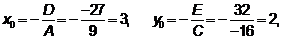
 ,
,
 ,
,
 .
.
4. По выражению 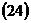 составим каноническое уравнение гиперболы
составим каноническое уравнение гиперболы
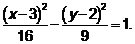 .
. 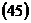
Уравнение 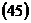 можно получить также преобразованием выражения
можно получить также преобразованием выражения
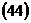 в соответствии с порядком вывода уравнения
в соответствии с порядком вывода уравнения 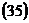 .
.
Преобразование  к виду уравнения параболы
к виду уравнения параболы 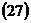 ,
, 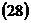
Имеем 
 .
.
1. Пусть  ,
, 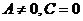 .
.
Тогда  принимает вид
принимает вид
 ,
,
 ,
,
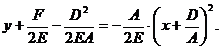

Получили:  имеет вид
имеет вид 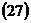 , где
, где 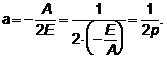
Здесь:
координаты вершины параболы 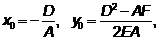

параметр параболы 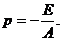

2. Пусть  ,
, 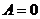 ,
, 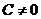
Тогда  примет вид
примет вид
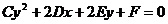 ,
,
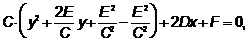 ,
,
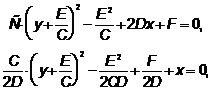
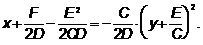 .
. 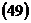
Получим: 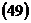 имеет вид
имеет вид 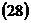 , где
, где 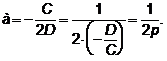 .
.
Здесь:
координаты вершины параболы 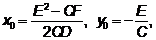 ,
, 
параметр параболы 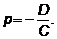 .
. 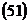
Пример 4 Составить уравнение множества точек, для каждой из которых расстояние до точки 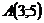 равно расстоянию до прямой
равно расстоянию до прямой 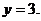
Решение.
1. Пусть 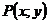 – произвольная точка заданного множества точек. По условию имеем
– произвольная точка заданного множества точек. По условию имеем

или 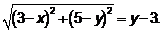 .
.
2. Приведем что выражение к виду  , получим
, получим

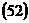
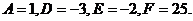
В уравнении 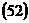
 что соответствует условию описания параболы и представления таким образом заданного множества точек.
что соответствует условию описания параболы и представления таким образом заданного множества точек.
3. По формулам  и
и  находим координаты вершины параболы
находим координаты вершины параболы  и
и 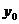
и параметр 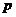 :
:
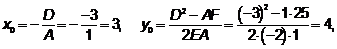

4. По выражению 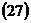 составим уравнение параболы
составим уравнение параболы

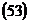
Уравнение 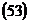 можно получить также преобразованием выражения
можно получить также преобразованием выражения
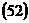 в соответствии с порядком вывода уравнения
в соответствии с порядком вывода уравнения 
Задача 3
Даны векторы 

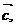
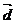 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы


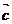 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 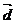 в этом базисе. Систему линейных уравнений решить методом Крамера.
в этом базисе. Систему линейных уравнений решить методом Крамера.
Например, 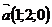 ,
, 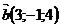 ,
, 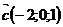 ,
, 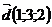 .
.
Решение
В задаче 3 изучается аффинная, общая декартова, система координат в трехмерном пространстве и формула разложения вектора на составляющие по осям координат или по базису.
Аффинной, или общей декартовой, системой координат в трехмерном пространстве называется совокупность трех объектов: заданной точки 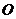 , называемой началом координат, заданных трех векторов
, называемой началом координат, заданных трех векторов 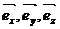 , не лежащих в одной плоскости (некомпланарных), образующих базис и называемых базисными, и трех прямых линий, проходящих через начало координат
, не лежащих в одной плоскости (некомпланарных), образующих базис и называемых базисными, и трех прямых линий, проходящих через начало координат 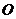 , совпадающих по направлению с базисными векторами и называемых координатными осями
, совпадающих по направлению с базисными векторами и называемых координатными осями 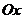 (ось абсцисс),
(ось абсцисс),  (ось ординат) и
(ось ординат) и  (ось аппликат) (рис.6).
(ось аппликат) (рис.6).
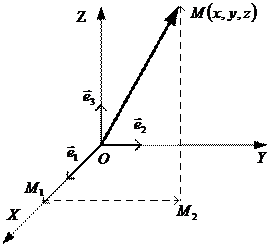
Рис.6
Декартова система координат обозначается  .
.
Плоскость, проходящая через пару координатных осей , называется координатной плоскостью и обозначается  , если проходит через оси
, если проходит через оси  и
и  ,
,  – через оси
– через оси  и
и  ,
, 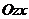 – через оси
– через оси 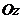 и
и 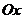 .
.
Система координат позволяет решить проблему однозначного определения положения произвольной точки 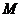 пространства с помощью упорядоченной тройки чисел
пространства с помощью упорядоченной тройки чисел  , называемых координатами точки
, называемых координатами точки 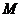 .
.
Для этого, используя линейные операции над векторами, представляют вектор 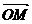 в виде
в виде
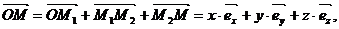

где 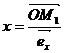 (абсцисса),
(абсцисса), 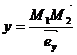 (ордината),
(ордината),  (аппликата) – аффинные координаты точки
(аппликата) – аффинные координаты точки 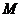 .
.
Формула  называется формулой разложения вектора
называется формулой разложения вектора 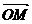 на составляющие по осям координат
на составляющие по осям координат 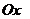 ,
, 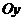 ,
, 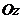 (по базису
(по базису  ).
).
Длина базисного вектора принимается за единицу длины на координатной оси.
Если углы между векторами базиса произвольны, но длины векторов равны, то система координат называется декартовой косоугольной, а координаты точки 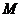 – косоугольными.
– косоугольными.
В частном случае, для базисных векторов 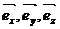 , попарно перпендикулярных и равных по длине, вводится соответствующее
, попарно перпендикулярных и равных по длине, вводится соответствующее
обозначение 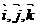 ; базисные векторы
; базисные векторы  называются ортами, базис
называются ортами, базис 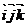 –
–
ортонормированным, общая декартова система координат  – прямоугольной ортонормированной.
– прямоугольной ортонормированной.
Формула  принимает вид:
принимает вид:
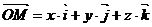 ,
, 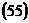
где 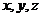 – прямоугольные координаты точки
– прямоугольные координаты точки 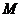 , численно выражающие величину ортогональных проекций вектора
, численно выражающие величину ортогональных проекций вектора 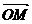 на ось абсцисс, ординат и аппликат соответственно;
на ось абсцисс, ординат и аппликат соответственно; 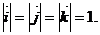
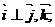

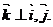

Пример. Обозначим векторы базиса, в котором даны векторы 

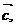
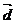 через
через 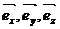 . Тогда в соответствии с данными численного примера по формуле
. Тогда в соответствии с данными численного примера по формуле  имеем
имеем
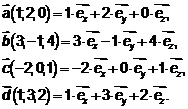
Для того, чтобы векторы 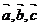 образовали базис, необходимо показать, что векторы некомпланарны и, следовательно, на этих векторах, как на сторонах, можно построить параллелепипед. Очевидно, что объем
образовали базис, необходимо показать, что векторы некомпланарны и, следовательно, на этих векторах, как на сторонах, можно построить параллелепипед. Очевидно, что объем 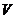 этого параллелепипеда не будет равным 0; если
этого параллелепипеда не будет равным 0; если 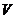 = 0, то векторы компланарны. В соответствии с геометрическим смыслом смешанного произведения
= 0, то векторы компланарны. В соответствии с геометрическим смыслом смешанного произведения 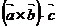 его абсолютная величина равна
его абсолютная величина равна
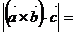
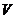 .
.
Отсюда следует, что если 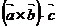
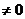 , то векторы
, то векторы 

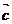 образуют базис.
образуют базис.
С помощью определителя 3-го порядка находим
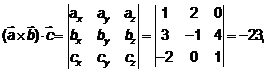 ,
,
где  – координаты перемножаемых векторов.
– координаты перемножаемых векторов.
Поскольку 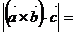 23
23 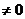 , то векторы
, то векторы 

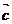 образуют базис.
образуют базис.
2. Найдём координаты вектора 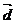 в базисе
в базисе  .
.
По формуле  имеем:
имеем:
 ,
, 

а также 


поскольку векторы 

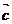 образуют базис, где
образуют базис, где 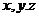 – координаты вектора
– координаты вектора 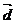 в базисе
в базисе  .
.
Подставим  в
в  :
:
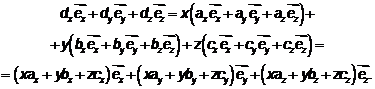
Откуда
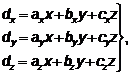 ,
, 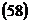
или
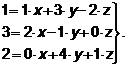 .
. 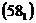
Получили систему 3-х линейных уравнений с 3-мя неизвестными 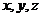 –координатами вектора
–координатами вектора 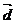 .
.
3. Решаем  методом Крамера, в соответствии с которым:
методом Крамера, в соответствии с которым:
1)система 3-х линейных уравнений с 3-мя неизвестными имеет единственное решение, если 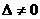 – определитель 3-го порядка, составленный из коэффициентов системы, не равен 0:
– определитель 3-го порядка, составленный из коэффициентов системы, не равен 0:
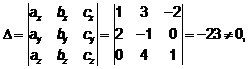
2)неизвестные 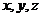 находим по формулам Крамера
находим по формулам Крамера

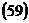
где 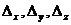 – определители 3-го порядка, составленные из определителя системы
– определители 3-го порядка, составленные из определителя системы 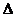 заменой коэффициентов, стоящих в
заменой коэффициентов, стоящих в 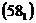 перед
перед 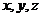 , свободными членами соответственно:
, свободными членами соответственно:
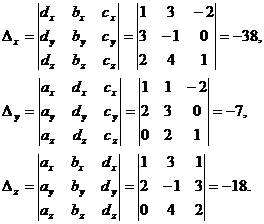
Тогда по формулам 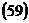 :
:
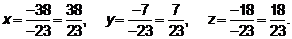
Проверка:
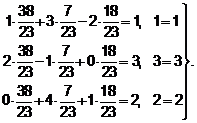 .
.
Получили тождество. Следовательно, система 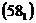 решена верно.
решена верно.
Ответ:
1)векторы 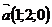 ,
, 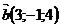 ,
, 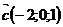 образуют базис,
образуют базис,
2)разложение вектора 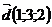 по базису
по базису  имеет вид
имеет вид
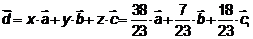 ,
,
где 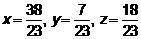 – координаты вектора
– координаты вектора 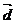 в базисе
в базисе  .
.
Задача 4
Применяя метод Гаусса исключения неизвестных, решить систему линейных уравнений. Сделать проверку найденного решения.
 Например:
Например:
(1) 2  –3
–3  +3
+3 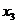 +2
+2  =3
=3
(2) 6  +9
+9  +2
+2 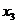 –
–  = –4
= –4
(3) 10 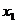 +3
+3  –3
–3 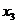 –2
–2  =3 (60)
=3 (60)
(4) 8 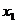 +6
+6  +
+ 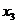 +3
+3  = –7 .
= –7 .
Решение
В задаче 4 изучается метод Гаусса решения систем линейных уравнений.
Метод Гаусса находит применение при решении систем уравнений в тех случаях, когда метод Крамера (метод определителей) оказывается слишком громоздким, что имеет место при решении систем линейных уравнений повышенной размерности, как правило, систем с числом уравнений и неизвестных более трех. Суть метода отражает его название: метод исключения неизвестных.
Путем элементарных преобразований системы линейных уравнений с помощью умножения и деления уравнений на действительные числа, сложения и вычитания уравнений можно получить систему, эквивалентную исходной, но в некоторых своих уравнениях с меньшим числом неизвестных.
Под эквивалентными системами мы понимаем такие системы, у которых равны численные значения соответствующих неизвестных. Подобное преобразование заданной системы имеет своей целью приведение её к системе треугольного вида, содержащей в последнем уравнении всего лишь одно неизвестное, а в предшествующих ему уравнениях увеличение числа неизвестных на 1. Очевидно, что такая система решается нахождением неизвестного из последнего уравнения с последующей его подстановкой в предшествующие уравнения и нахождения из них всех остальных неизвестных.
Изложенное проиллюстрируем на примере.
1. В системе (60) прежде всего избавимся от 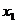 во 2-м, 3-м и 4-м уравнениях.
во 2-м, 3-м и 4-м уравнениях.
Для этого:
а) разделим каждое из уравнений на коэффициент при х1, получим:
 (60
(60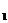 )
)
б) из 2-го, 3-го и 4-го уравнений вычтем 1-ое

 . (60
. (60  )
)
2. Аналогично предыдущему избавляемся теперь от  в 3-м и 4-м уравнениях:
в 3-м и 4-м уравнениях:
а) разделим 2-е, 3-е и 4-е уравнения на коэффициент при 
 , (60
, (60 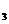 )
)
б) из 3-го и 4-го уравнений вычтем 2-е
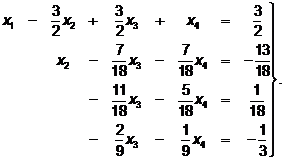 . (60
. (60  )
)
3. Избавляемся от 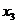 в 4-м уравнении:
в 4-м уравнении:
а) разделим 3-е и 4-е уравнения на коэффициент при 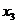 :
:
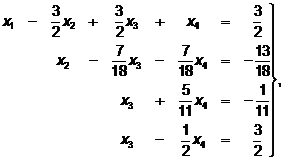 (60
(60  )
)
б) из 4-го уравнения вычтем 3-е
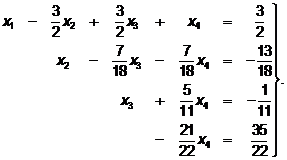 (60
(60  )
)
Получили систему уравнений – (60 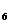 ) , эквивалентную заданной (60), но треугольного вида, в которой последнее уравнение содержит одно неизвестное
) , эквивалентную заданной (60), но треугольного вида, в которой последнее уравнение содержит одно неизвестное  , а во всех предшествующих ему уравнениях число неизвестных увеличивается на 1.
, а во всех предшествующих ему уравнениях число неизвестных увеличивается на 1.
4. Из 4-го уравнения находим  , затем, используя полученный результат, последовательно: из 3-го -
, затем, используя полученный результат, последовательно: из 3-го - 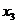 , из 2-го –
, из 2-го –  , из 1- го –
, из 1- го – 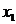 . Получим:
. Получим:
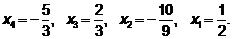
Выполненные элементарные преобразования системы уравнений (60) предусматривали определенный алгоритм приведения системы (60) к треугольному виду путем деления уравнений на коэффициенты при неизвестных и вычитания уравнений. Алгоритм может быть и другим, использующий и операции умножения и сложения, а также перестановку уравнений и удаление из рассмотрения тривиального уравнения, в котором все коэффициенты при неизвестных и свободный член равны нулю.
5. Проверка. Подставляя значения неизвестных 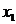 ,
,  ,
, 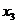 ,
,  в заданную систему (60), необходимо получить тождество в каждом уравнении:
в заданную систему (60), необходимо получить тождество в каждом уравнении:
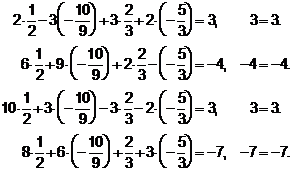
В каждом уравнении получено тождество. Задача решена верно.
Ответ: 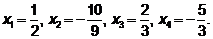
Выполненные преобразования связаны с преобразованием коэффициентов и свободных членов системы уравнений, поэтому они могут быть осуществлены в более компактном матричном виде без переписывания обозначений самих неизвестных.
Мы рассмотрели систему (60), которая имеет единственное решение. Системы, имеющие единственное решение, называются определенными. Системы линейных уравнений, имеющие бесчисленное множество решений, называются неопределенными, а не имеющие ни одного решения – несовместными.
Несовместная система всегда содержит противоречивое уравнение вида:
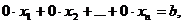 где
где 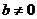 .
.
И определенные и неопределенные системы относятся к совместным.
Метод Гаусса исключения неизвестных предоставляет возможность не только получить решение определенной и неопределенной систем линейных уравнений, но и обнаружить противоречивое уравнение и на этом основании сделать заключение о несовместности системы.
В задачах экономики широкое применение получили элементарные преобразования систем линейных уравнений, известные под названием жордановых преобразований, а также связанный с ними метод Жордана –Гаусса решения систем линейных уравнений. Метод Жордана-Гаусса предполагает выполнение следующих элементарных преобразований. В каждом из уравнений системы произвольно выберем одно из неизвестных, но так, чтобы этот выбор не повторить в остальных уравнениях. Коэффициент при выбранном неизвестном и само неизвестное назовем разрешающим.
Пусть в рассмотренном выше примере разрешающими неизвестными будут: в 1-м уравнении 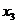 , во 2-м
, во 2-м  , в 3-м
, в 3-м 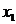 , в 4-м
, в 4-м  .
.
1. Избавимся от 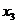 во 2-м, 3-м, и 4-м уравнениях. Для этого выполним
во 2-м, 3-м, и 4-м уравнениях. Для этого выполним
такие действия, чтобы коэффициенты при 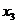 во 2-м , 3-м, 4-м уравнениях приравнять коэффициенту при
во 2-м , 3-м, 4-м уравнениях приравнять коэффициенту при 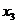 в 1-м уравнении, но с противоположным знаком и к каждому из этих уравнений прибавим 1-е уравнение.
в 1-м уравнении, но с противоположным знаком и к каждому из этих уравнений прибавим 1-е уравнение.
Умножая 2-е уравнение на -3/2, 3-е на 1, 4-е на -3 и прибавляя к ним 1-е уравнение, получаем:
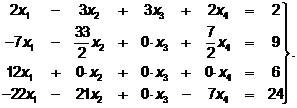 (60
(60 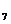 )
)
2. Выполним жорданово преобразование системы (60 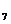 ) относительно неизвестной
) относительно неизвестной  2-го уравнения. Для этого необходимо избавиться от
2-го уравнения. Для этого необходимо избавиться от  в 1-м, 3-м и 4-м уравнениях. Однако, в результате предыдущего преобразования в 3-м уравнении уже получен при
в 1-м, 3-м и 4-м уравнениях. Однако, в результате предыдущего преобразования в 3-м уравнении уже получен при  коэффициент равный 0, а само уравнение оказалось разрешенным относительно
коэффициент равный 0, а само уравнение оказалось разрешенным относительно 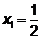 . Поэтому умножаем 1-е уравнение на
. Поэтому умножаем 1-е уравнение на 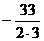 , 3-е уравнение не изменяем, 4-е умножаем на
, 3-е уравнение не изменяем, 4-е умножаем на 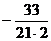 и прибавляем к 1- му и 4- му уравнениям 2-ое уравнение, получаем:
и прибавляем к 1- му и 4- му уравнениям 2-ое уравнение, получаем:
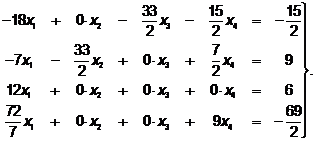 . (60
. (60 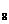 )
)
Из (60  ) видно, что продолжить решение можно было бы методом подстановки, выражая
) видно, что продолжить решение можно было бы методом подстановки, выражая 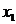 из 3-го и подставляя в 4-е уравнение, чтобы найти
из 3-го и подставляя в 4-е уравнение, чтобы найти  . Полученные
. Полученные 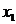 и
и  , будучи подставленными в 1-е и 2-е уравнения, позволяют найти
, будучи подставленными в 1-е и 2-е уравнения, позволяют найти 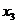 и
и  . Но мы продолжим изучать жорданово преобразование.
. Но мы продолжим изучать жорданово преобразование.
3. Выполним жорданово преобразование системы (60 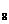 ) относительно неизвестной
) относительно неизвестной 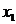 3-го уравнения, избавляясь от коэффициентов при
3-го уравнения, избавляясь от коэффициентов при 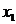 в 1-м,
в 1-м,
2-м и 4-м уравнениях . Для этого умножим 1-е уравнение на 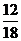 , 2-е на
, 2-е на 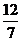 , 4-е на
, 4-е на  и прибавим к каждому из этих уравнений 3-е уравнение, получим:
и прибавим к каждому из этих уравнений 3-е уравнение, получим:
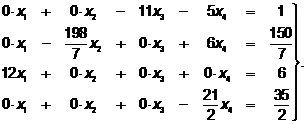 . (60
. (60  )
)
Систему (60  ),как и (60
),как и (60 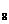 ), можно решить методом подстановки. Однако, как и в предыдущем случае, продолжаем применять жорданово преобразование теперь уже к системе (60
), можно решить методом подстановки. Однако, как и в предыдущем случае, продолжаем применять жорданово преобразование теперь уже к системе (60  )относительно неизвестной
)относительно неизвестной  4-го уравнения.
4-го уравнения.
4. Умножаем 1-е уравнение на 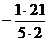 , 2-е на
, 2-е на 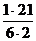 и прибавляем 4-е уравнение, получим:
и прибавляем 4-е уравнение, получим:
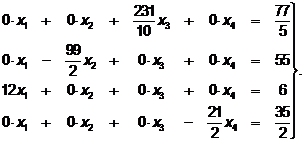 . (60
. (60 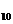 )
)
В результате получим разрешенную систему (60 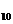 ), в которой каждое уравнение является разрешенным и позволяет найти:
), в которой каждое уравнение является разрешенным и позволяет найти:
из 1-го уравнения 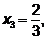 , из 2-го
, из 2-го 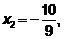 , из 3-го
, из 3-го 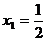 , из 4-го
, из 4-го  .
.
5. Значения неизвестных, полученные по методу Гаусса и Жордана-Гаусса
совпадают, что подтверждает правильность выполненных расчетов.
Задача 5
Следующая задача об экстремумах функций двух переменных и об отыскании наибольших и наименьших значений функции двух независимых переменных. Функция ограниченная и дифференцируемая в замкнутой области достигает в этой области своего наибольшего и наименьшего значения или во внутренних точках этой области, которые являются точками стационарности функции или на её границе. Для того, чтобы найти наибольшее и наименьшее значение функции, надо:
1) Найти стационарные точки функции, для чего следует решить систему уравнений  .
.
2) Вычислить в стационарных точках значения функции
3) Найти наибольшие и наименьшее значение функции на каждой линии, ограничивающей область;
4) Сравнить все полученные значения. Наибольшее из них будет наибольшим, а наименьшее – наименьшим значением функции в замкнутой области.
Пример. Найти наибольшее и наименьшее значение функции 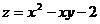 в ограниченной замкнутой области D:
в ограниченной замкнутой области D: 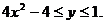
Решение
Точка 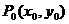 являются точкой экстремума (максимума или минимума) функции z=f(x,y), если значение функции в этой точке соответственно больше или меньше значений, принимаемых ее в некоторой окрестности точки
являются точкой экстремума (максимума или минимума) функции z=f(x,y), если значение функции в этой точке соответственно больше или меньше значений, принимаемых ее в некоторой окрестности точки  , то есть при всех x и y достаточно близких к
, то есть при всех x и y достаточно близких к  и
и 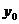 . Точка P, координаты которой обращают в нуль обе частные производные функции f(x,y) называются стационарной точкой этой функции.
. Точка P, координаты которой обращают в нуль обе частные производные функции f(x,y) называются стационарной точкой этой функции.
1. Найдем стационарные точки функции z(x,y)

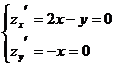
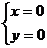
Стационарная точка y функции z одна. Это точка 0.
2. Входит ли точка (0,0) в область D? Построим эту область.
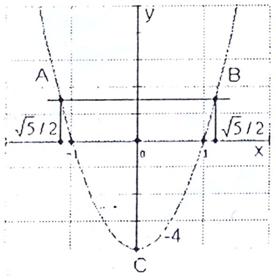
- 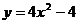 - парабола с вершиной в точке (0,-4). Точки пересечения с осью x:
- парабола с вершиной в точке (0,-4). Точки пересечения с осью x: 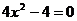 ,
, 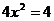 ,
, 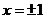
- y=0 – ось x.
Точка (0,0) входит в область D. Установим, является ли стационарная точка 0 точкой экстремума. Это делается так: Пусть  стационарная точка функции z=f(x,y). Вычислим в этой точке
стационарная точка функции z=f(x,y). Вычислим в этой точке
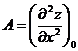 .
. 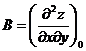 .
. 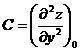
Если 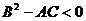 , то функция f(x,y) имеет в точке
, то функция f(x,y) имеет в точке  экстремум:
экстремум:
max – при A<0 и min – при A>0.
Если 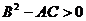 , то точка
, то точка  не является точкой экстремума.
не является точкой экстремума.
Если  , то требуется дополнительное исследование.
, то требуется дополнительное исследование.
Исследуем нашу функцию z по формулам.
3. 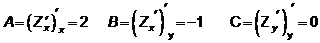
 , точка (0,0) не является точкой экстремума.
, точка (0,0) не является точкой экстремума.
4. Исследуем поведение функции на границе.
Так как Z не имеет ни max ни min, ее наибольшим и наименьшем значением является наибольшее и наименьшее из значений, принимаемых на границе.
Для того чтобы найти наибольшее или наименьшее из значений, принимаемых на границе.
4а. Рассмотрим верхнюю границу y=1. На ней функция Z(x,1) превращается в 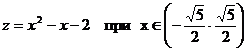
 ,
,  в этой точке возможен экстремум. Знак производной меняется с – на +, то есть в точке
в этой точке возможен экстремум. Знак производной меняется с – на +, то есть в точке  - минимум z =-2.25
- минимум z =-2.25
при 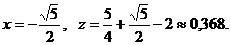
В точке 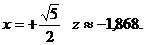
4б. Рассмотрим нижнюю границу 
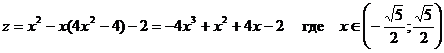

В точке 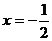 производная меняет знак с - на +, следовательно, это точка минимума
производная меняет знак с - на +, следовательно, это точка минимума 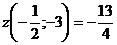

В точке 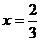 производная меняет знак с + на -, следовательно, это точка максимума
производная меняет знак с + на -, следовательно, это точка максимума 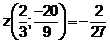 . При
. При  функция z уже вычислялось. Видим, что от
функция z уже вычислялось. Видим, что от 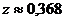 функция убывает до
функция убывает до 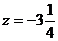 , затем возрастает до
, затем возрастает до  а затем убывает до
а затем убывает до 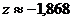 .
.
То есть наименьшее значение для всей границы 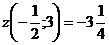 , а наибольшее
, а наибольшее 
Ответ: Наибольшее значение функции z в замкнутой области D 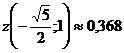 , наименьшее
, наименьшее  .
.
Задача 6
Найтиобщее решение линейного дифференциального уравнения.
Сформулируем общее правило нахождения решения линейного однородного дифференциального уравнения с постоянными коэффициентами.
1) Составляем характеристическое уравнение и находим его корни.
2) Находим частные решения дифференциального уравнения, причем:
a) каждому действительному корню соответствует решение ekx;
б) каждому действительному корню кратности m ставится в соответствие m решений:
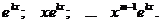
в) каждой паре комплексно – сопряженных корней 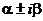 характеристического уравнение ставится в соответствие два решения:
характеристического уравнение ставится в соответствие два решения:
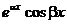 и
и 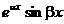 .
.
г) каждой паре m – кратных комплексно – сопряженных корней 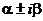 характеристического уравнения ставится в соответствие 2m решений:
характеристического уравнения ставится в соответствие 2m решений:

3) Составляем линейную комбинацию найденных решений.
Эта линейная комбинация и будет являться общим решением исходного линейного однородного дифференциального уравнения с постоянными коэффициентами.
Пример 1. Решить уравнение 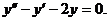
Характеристическое уравнение: 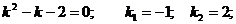
Общее решение: 
Пример 2. Решить уравнение 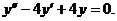
Характеристическое уравнение: 
Общее решение: 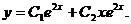
Пример 3. Решить уравнение 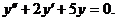
Характеристическое уравнение: 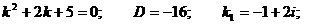
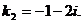
Общее решение: 
Заметим, что тот же способ применяется для решения линейных однородных дифференциальных уравнений с постоянными коэффициентами и более высоких порядков.
Рекомендуемая литература
Основная литература
1. Высшая математика для экономического бакалавриата: учебник и прак-тикум / Н.Ш. Кремер [и др.]; под ред. Н.Ш. Кремера. ― 4-е изд.; перераб. и доп. ― М.: Юрайт, 2012, 2014 ― ЭБС Юрайт.
2. Математика для экономистов и менеджеров [электронный ресурс]: Ученик / под ред. Н.Ш. Кремера. – М.: Кнорус, 2015. ЭБС: book.ru
3. Математика для экономистов и менеджеров [электронный ресурс]: Прак-тикум : учебное пособие / Н.Ш. Кремер, Б.А. Путко, М.Н. Фридман / под ред. Н.Ш. Кремера. – М.: Кнорус, 2015. ЭБС: Book.ru
4. Высшая математика [электронный ресурс]: Учебник и практикум для ака-демического бакалаврата / М. Б. Хрипунова [и др.] ; под общ. ред. М. Б. Хрипуновой, И. И. Цыганок. — М. : Издательство Юрайт, 2017 ― ЭБС Юрайт.
Дополнительная литература
5. Математика в экономике. Ч.1: Линейная алгебра, аналитическая геометрия и линейное программирование: учебник / А.С.Солодовников [и др.]. — 3-е изд., перераб. и доп. — М.: Финансы и статистика; ИНФРА-М, 2011.
6. Сборник задач по курсу "Математика в экономике". В 3 ч. Ч. 1: Линейная алгебра, аналитическая геометрия и линейное программирование: учебное пособие / под ред. В.А. Бабайцева и В.Б. Гисина.— М.: Финансы и стати-стика, 2013.
7. Математика в экономике. Ч.2: Математический анализ: учебник / А.С.Солодовников [и др.]. — 3-е изд., перераб. и доп. — М.: Финансы и статистика; Инфра-М, 2011 .
8. Сборник задач по курсу "Математика в экономике". В 3 ч. Ч. 2: Математи-ческий анализ: учебное пособие / под ред. В.А. Бабайцева и В.Б. Гисина. — М.: Финансы и статистика, 2013.
9. Красс М.С. Основы математики и ее приложения в экономическом образо-вании: учебник / М.С. Красс, Б.П. Чупрынов – 5-е изд., испр. и доп. – М.: Дело, 2006.
10. Красс М.С. Математика для экономических специальностей: учебник / М.С. Красс . – 4. изд., испр. – М.: Дело, 2005, 2002.
11. Кремер Н.Ш. Математика для экономистов: от арифметики до эконо-метрики: учебно-справочное пособие / Кремер Н.Ш., Путко Б.А., И.М. Тришин.; Финуниверситет; под ред. Н.Ш. Кремера.— 4-е изд., перераб. и доп.— М.: Юрайт, 2015.— 724с.— ЭБС Юрайт.
12. Simon C.P. Mathematics for Economists / C.P. Simon, L. Blume . – Norton Company. N.-Y., 1994.
13. Dowling E. Mathematical Economics / E. Dowlin . – Shaum’s Outline Se-ries. N.-Y., 2006
Перечень ресурсов информационно-коммуникационной сети «Интернет»
1. Информационно-образовательный портал Финансового университета при Правительстве Российской Федерации http://portal.ufrf.ru/.
2. Сайт департамента анализа данных, принятия решений и финансовых технологий. http://fa.ru/dep/data_analysis/
3. Библиотечно – информационный комплекс Финуниверситета при Правительстве РФ. http://library.fa.ru.
4. Репозиторий Финуниверситета при Правительстве РФ.
http://repository.vzfei.ru.
Дата добавления: 2018-04-05; просмотров: 230; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
