Лекция 2 Решение систем линейных уравнений
Лекция 1 Матрицы и матричные операции
Матрицей размерности m×n называется совокупность чисел, расположенных в виде таблицы, содержащей m строк и n столбцов.
Если матрица состоит из одной строки, то она называется матрицей – строкой размерности 1×n.
Если матрица состоит из одного столбца, то она называется матрицей – столбцом размерности m×1.
При n=m матрица называется квадратной матрицей n–го порядка.
Элементы матрицы, aij, у которых номер строки равен номеру столбца, называются диагональными и образуют главную диагональ матрицы.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
Если у диагональной матрицы n–го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n–го порядка, она обозначается E.
Матрица любого размера называется нулевой, или нуль – матрицей, если все её элементы равны нулю.
Рассмотрим операции над матрицами.
1. Сложение (вычитание) матриц.
Суммой (разностью) матриц A и B одинакового типа называется матрица C того же типа, элементы которой равны сумме (разности) соответствующих элементов исходных матриц A и B.
2. Умножение матрицы на число.
Произведением матрицы A на число 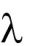 называется матрица C того же типа, что и A, элементы которой равны произведению соответствующих элементов матрицы A на число . Возможно сделать и обратную опера-цию: упростить элементы матрицы вынесением за матрицу общего множителя.
называется матрица C того же типа, что и A, элементы которой равны произведению соответствующих элементов матрицы A на число . Возможно сделать и обратную опера-цию: упростить элементы матрицы вынесением за матрицу общего множителя.
|
|
|
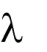
3. Умножение матрицы на матрицу.

Произведением матрицы A размера ( m1 n1)на матрицу B размера


| ( m 2 n2) называется матрица C размера ( m1 | n2) ,элементы которой оп- | ||||||
| ределяются по формуле: | |||||||
| n1 | , ( i=1,2....m1; | j=1,2...n2). | |||||
| C | a | b | (1.1) | ||||
| i , j | k | i , k | k , j | ||||
| 1 | |||||||

Умножение матриц возможно в случае, когда число столбцов матрицы A равно числу строк матрицы B.
4. Операция транспонирования матрицы.
Операция транспонирования заключается в перемене местами строк и столбцов с сохранением их номеров.
Определителем (детерминантом) n-го порядка квадратной мат  рицы A(n х n) называется алгебраическая сумма всех возможных произведений ее элементов, взятых по одному из каждой строки и каждого столбца. Причем знак каждого слагаемого определяется числом инверсий в перестановках из первых и вторых индексов членов сомножителей.
рицы A(n х n) называется алгебраическая сумма всех возможных произведений ее элементов, взятых по одному из каждой строки и каждого столбца. Причем знак каждого слагаемого определяется числом инверсий в перестановках из первых и вторых индексов членов сомножителей.
|
|
|
Общая формула расчета определителя выражается:
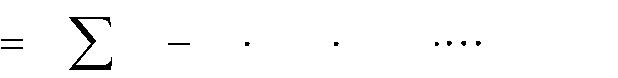
| det A | ( 1)t a | a | a | , |
| |
| 1, j1 | 2, j 2 | n , jn |
j1, j2... jn
где j – индексы столбцов определителя; t – число инверсий в перестановке индексов столбцов.
Недостатком данного метода является его громоздкость. При вычислении определителей выше третьего порядка резко возрастает объем вычислений.
Метод вычисления определителя разложением его по элементам строки или столбца основан на теореме: любой определитель можно представить в виде суммы произведений элементов произвольной его строки или столбца на соответствующие алгебраические дополнения Аi,j:
| n | n | ||
| det A | aik Ai , k | aki Ak ,i(i 1,2, , n),. | |
| k | 1 | k 1 |

Под алгебраическим дополнением (Ai,j) определителя D понимается дополнительный минор к элементу ai,j:

Ai , j ( 1)i j M ,
где i, j – номера строки и столбца элемента.
Разложение определителя по элементам столбца или строки проще всего, когда в этой строке или столбце имеется единственный ненулевой элемент. Тогда определитель равен произведению этого элемента на его алгебраическое дополнение. К такому виду можно преобразовать определитель путем операций над его строками или столбцами, используя его основные свойства.
|
|
|
Наиболее просто вычисляется определитель диагональной и треугольной матрицы. Он равен произведению его диагональных элементов. Метод заключается в преобразовании исходного определителя путем элементарных операций, основанных на свойствах определителя, к диагональной или треугольной форме.
Лекция 2 Решение систем линейных уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется система вида
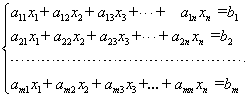 (1)
(1)
Решением системы (1) называется такая совокупность n чисел 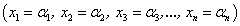 , при подстановке которых каждое уравнение системы обращается в верное равенство.
, при подстановке которых каждое уравнение системы обращается в верное равенство.
Решить систему означает найти все ее решения или доказать, что ни одного решения нет.
СЛАУ называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.
Если совместная система имеет только одно решение, то она называется определенной, и неопределенной, если она имеет более чем одно решение.
Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений. В частности, две несовместные системы считаются эквивалентными.
|
|
|
Основной матрицей СЛАУ (1) называется матрица А размера 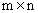 , элементами которой являются коэффициенты при неизвестных данной системы, то есть
, элементами которой являются коэффициенты при неизвестных данной системы, то есть
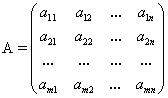 .
.
Матрицей неизвестных СЛАУ (1) называется матрица-столбец Х, элементами которой являются неизвестные системы (1):
 .
.
Матрицей свободных членов СЛАУ (1) называется матрица-столбец В, элементами которой являются свободные члены данной СЛАУ:
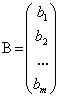 .
.
С учетом введенных понятий СЛАУ (1) можно записать в матричном виде 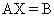 или
или
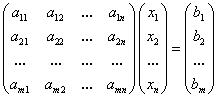 . (2)
. (2)
Рассмотрим в общем виде систему уравнений АХ = В с невырожденной квадратной матрицей А. В этом случае существует обратная матрица А-1. Домножим слева обе части на А-1. Получим А-1АХ = А-1В. Отсюда ЕХ = А-1В и Х = А-1В.
Последнее равенство представляет собой матричную формулу для нахождения решения таких систем уравнений. Использование этой формулы получило название метода обратной матрицы
Правило и формулы Крамера
Рассмотрим систему 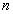 линейных уравнений с
линейных уравнений с 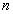 неизвестными
неизвестными
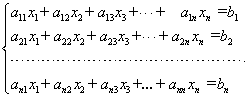
Учитывая равенство 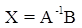 , или в развернутом виде
, или в развернутом виде
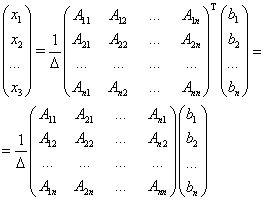 .
.
Таким образом, после перемножения матриц получаем:
 или
или
 .
.
Заметим, что сумма  есть разложение определителя
есть разложение определителя
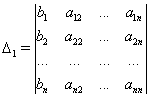
по элементам первого столбца, который получается из определителя  путем замены первого столбца коэффициентов столбцом из свободных членов.
путем замены первого столбца коэффициентов столбцом из свободных членов.
Таким образом, можно сделать вывод, что 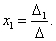
Аналогично: 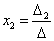 , где
, где  получен из
получен из  путем замены второго столбца коэффициентов столбцом из свободных членов,
путем замены второго столбца коэффициентов столбцом из свободных членов,  .
.
Следовательно, нами найдено решение заданной системы по равенствам
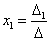 ,
, 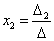 ,
,  ,
,
известным, как формулы Крамера.
Для нахождения решения СЛАУ, последние равенства можно записать в общем виде следующим образом:
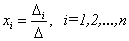 .
.
Согласно этим формулам, имеем правило Крамера для решения СЛАУ:
по матрице системы  вычисляется определитель системы
вычисляется определитель системы  ;
;
если 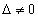 , то в матрице системы каждый столбец последовательно заменяется столбцом свободных членов и вычисляются определители
, то в матрице системы каждый столбец последовательно заменяется столбцом свободных членов и вычисляются определители 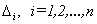 получаемых при этом матриц; решение системы находится по формулам Крамера.
получаемых при этом матриц; решение системы находится по формулам Крамера.
Лекция 3 Комплексные числа
Комплексным числом называется число вида z = x +iy, где x и y – действительные числа, i – мнимая единица, то есть число, квадрат которого равен (минус) –1, x – действительная часть, y – мнимая часть.
Если x = 0, то число z = iy чисто мнимое.
Запись z = x + iy – алгебраическая форма записи числа.
Два комплексных числа z1 = x1+iy1и z2=x2+iy2называются равными (z1=z2) тогда и только тогда, когда равны их действительные части и равны их мнимые части: x1=x2, y1=y2. Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Два комплексных числа вида z = x + iy и z = x – iy называются комплексно-сопряженными.
Всякое комплексное число z = x + iy можно изобразить точкой М(x,y) на плоскости Оxy и, наоборот, каждую точку М(x,y) координатной плоскости можно рассматривать как образ комплексного числа z = x + iy.
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Комплексное число z = x + iy можно также изобразить в виде радиус-вектора r = ОМ.
Длина вектора r = │ОМ│ называется модулем комплексного числа.
Угол φ, образованный вектором OM с положительным направлением оси Ox называется аргументом комплексного числа: φ = Arg z.
Аргумент комплексного числа величина многозначная Arg z = arg z +2πk, где arg z – главное значение аргумента, – π < arg z <+ π (или [0, 2π)). Угол φ таков, что cos φ = x/r; sin φ = y/ r.
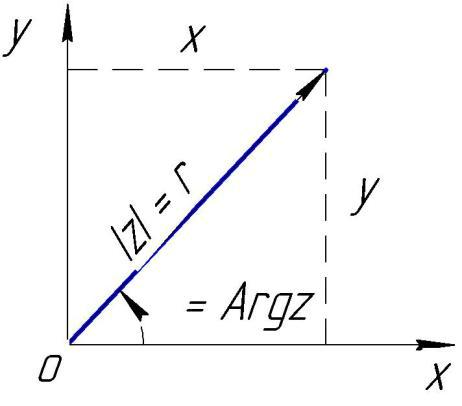
Если x и y - декартовы координаты точки плоскости, то, перейдя на плоскости к полярным координатам (r, φ) и воспользовавшись связью x = rcos φ, y = rsin φ получим тригонометрическую форму записи комплексного числа:
z = r (cos φ + isin φ) .
При решении задач для вычисления аргумента удобно пользоваться схемой, приведенной ниже:

Используя формулу Эйлера еiφ= cos φ+isin φ получим показательную формузаписи комплексного числа: Z= z еiφ
Cуммой комплексных чисел z1 и z2 называется комплексное число z вида z = (x1 + x2; y1 + y2).
Произведением комплексных чисел z1 и z2 называется комплексное число z = (x1x2 – y1y2; x1y2 + x2y1).
Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что z2 + z = z1, откуда находим z = z1 – z2 = (x1 – x2, y1 – y2).
 Частным комплексных чисел z1 и z2 называется комплексное число z такое, что
Частным комплексных чисел z1 и z2 называется комплексное число z такое, что  .
.
Лекция 4 Дробно-рациональные функции
Дробно-рациональные функции комплексного переменного в различных формах широко используют в ТАУ для представления передаточных функций и решения задач синтеза и анализа САУ.
Дробно-рациональная функция некоторого действительного или комплексного переменного  имеет следующий вид:
имеет следующий вид:

| (1) |
где  - полиномы числителя и знаменателя,
- полиномы числителя и знаменателя,  - действительные числа,
- действительные числа, 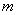 - порядок числителя,
- порядок числителя, 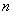 - порядок знаменателя (всей дробно-рациональной функции функции),
- порядок знаменателя (всей дробно-рациональной функции функции), 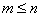 - для функций используемых в ТАУ.
- для функций используемых в ТАУ.
Полиномы дробно-рациональной функции могут быть представлены в виде произведения биномов (разложение многочлена на сомножители), тогда функция может быть представлена в форме Боде
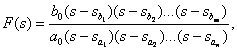
| (2) |
где 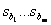 - корни уравнения
- корни уравнения 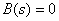 ,
, 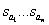 - корни характеристического уравнения
- корни характеристического уравнения 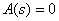 .
.
Корни уравнения 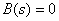 называют нулями дробно-рациональной функции
называют нулями дробно-рациональной функции  , так как
, так как
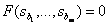 .
.
Корни характеристического уравнения 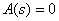 называют полюсами дробно-рациональной функции, так как
называют полюсами дробно-рациональной функции, так как
 .
.
Полюсы и нули могут быть действительными и комплексно-сопряженными числами. Таким образом, задача представления функции в форме Боде сводится к поиску корней уравнений, образованных полиномами числителя и знаменателя.
Их принято располагать на плоскости комплексной переменной  , обозначая расположение полюсов крестиками, а нулей кружками. Для лучшего освоения этого материала необходимо освежить в памяти сведения из высшей математики по операциям с комплексными числами. Нули, а особенно полюсы дробно-рациональных функций изображают на плоскости комплексного переменного
, обозначая расположение полюсов крестиками, а нулей кружками. Для лучшего освоения этого материала необходимо освежить в памяти сведения из высшей математики по операциям с комплексными числами. Нули, а особенно полюсы дробно-рациональных функций изображают на плоскости комплексного переменного 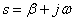 . На рис. 1 показано расположение полюсов и нулей некоторой дробно-рациональной функции.
. На рис. 1 показано расположение полюсов и нулей некоторой дробно-рациональной функции.
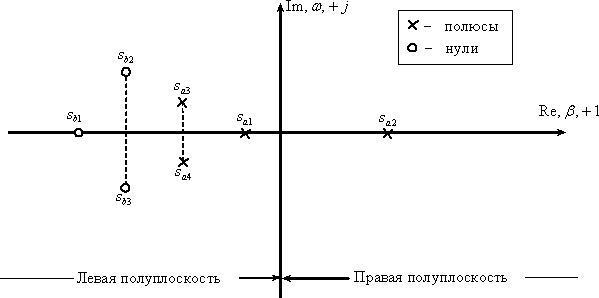
Рис. 1
Мнимая ось делит плоскость  на правую и левую полуплоскости. Нули и полюсы, расположенные в правой полуплоскости, называют правыми, в левой полуплоскости – левыми. Комплексные полюсы и нули всегда располагаются парами симметрично относительно действительной оси; такие пары корней называют комплексно сопряженными корнями. Если среди нулей и полюсов встречаются два или несколько одинаковых, их называют кратными в отличие от остальных, которых называют простыми. Кратность определяется числом одинаковых нулей или полюсов (
на правую и левую полуплоскости. Нули и полюсы, расположенные в правой полуплоскости, называют правыми, в левой полуплоскости – левыми. Комплексные полюсы и нули всегда располагаются парами симметрично относительно действительной оси; такие пары корней называют комплексно сопряженными корнями. Если среди нулей и полюсов встречаются два или несколько одинаковых, их называют кратными в отличие от остальных, которых называют простыми. Кратность определяется числом одинаковых нулей или полюсов ( 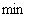 – 2). Рассмотрим пример получения формы Боде.
– 2). Рассмотрим пример получения формы Боде.
Пример
Представьте дробно-рациональную функцию
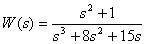
в форме Боде и покажите расположение полюсов и нулей дробно-рациональной функции на комплексной плоскости.
Решение
Найдем корни уравнения
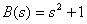 .
.
Получаем два комплексно-сопряженных корня (нуля)
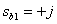 ,
, 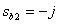 .
.
Найдем полюсы 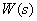
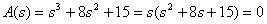 .
.
Получаем три полюса
 .
.
Покажем расположение нулей и полюсов на комплексной плоскости (см. рис. 2).
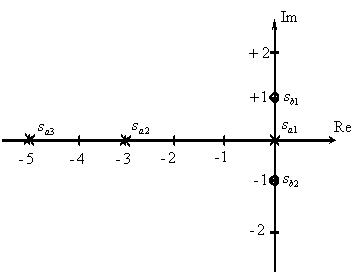
Рис. 2
Дробно-рациональную функцию (1) часто представляют в виде суммы простейших дробей (форма Хэвисайта)

| (3) |
где  - корни характеристического уравнения
- корни характеристического уравнения 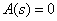 ,
,  - коэффициенты разложения, которые находят по следующей функции:
- коэффициенты разложения, которые находят по следующей функции:

| (4) |
Такое представление дробно-рациональной функции возможно, если полюсы  – простые, а
– простые, а 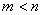 .
.
Функция, которая имеет один нулевой полюс, может быть представлена в следующем виде:
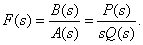
В этом случае вместо формул (3), (4) применяют выражение
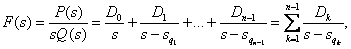
| (5) |
где  - ненулевые полюсы
- ненулевые полюсы  , корни уравнения
, корни уравнения  ,
,

| (6) |
Следовательно, представление дробно-рациональной функции в форме Хэвисайта сводится к нахождению полюсов дробно-рациональной функции и рациональному использованию формул разложения. Рассмотрим ряд примеров получения формы Боде.
Пример
Представьте дробно-рациональную функцию
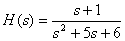
в форме Хэвисайта, используя формулы разложения (3), (4).
Решение
Уравнение полинома числителя имеет вид
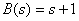 .
.
Характеристическое уравнение имеет вид
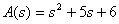 .
.
Найдем корни характеристического уравнения
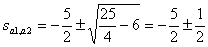 ,
, 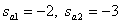 .
.
Определим производную от полинома знаменателя
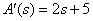 .
.
Определим коэффициенты разложения соответствующие по номеру полюсам
 ,
,  .
.
Тогда форма Хэвисайта имеет вид
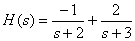 .
.
Пример
Представьте дробно-рациональную функцию

в форме Хэвисайта, используя формулы разложения (5), (6).
Решение
Представим  в виде
в виде
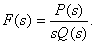
Тогда
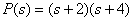 ,
,
 .
.
Ненулевые полюсы имеют вид
 ,
, 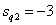 .
.
Производная от 
 .
.
Определим коэффициенты разложения
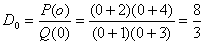 ,
,  ,
, 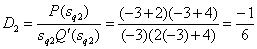 .
.
Тогда форма Хэвисайта имеет вид
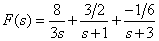 .
.
Импульсные функции
Реальные сигналы (переменные и воздействия), встречающиеся в системах управления, обычно представляют с помощью некоторых идеализаций – импульсных функций. Чаще всего используют ступенчатую единичную функцию (функцию Хэвисайта) и дельта-функцию (функцию Дирака), которые описываются следующим образом:
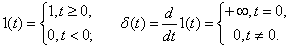
Графики этих функций показаны на рис. 3.
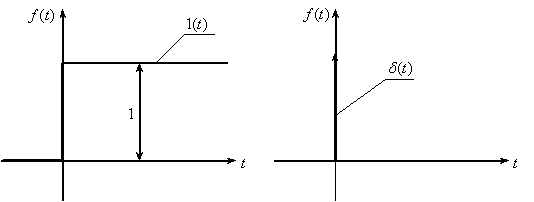
Рис. 3
Для единичной и дельта-функции справедливо
 .
.
Таким образом, дельта-функция представляет собой мгновенный импульс, равный бесконечности в нулевой момент времени и нулю в другие моменты, площадь которого постоянна и равна единице. Поэтому иногда 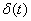 называют единичным импульсом.
называют единичным импульсом.
Контрольные вопросы и задачи
1. Как определить порядок дробно-рациональной функции?
2. Поясните процедуру преобразования функции к форме Боде.
3. Какие полюсы дробно-рациональной функции называют простыми?
4. В чем состоит идеализация представления реального сигнала единичной ступенчатой функцией?
5. Представьте дробно-рациональную функцию
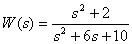
в форме Боде.
Ответ:
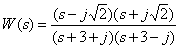 .
.
6. Представьте дробно-рациональную функцию
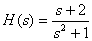
в форме Хэвисайта.
Ответ:
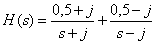 .
.
7. Представьте дробно-рациональную функцию
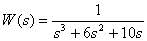
в форме Хэвисайта.
Ответ:
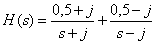 .
.
Лекция 5 Преобразование Фурье
Соотношение
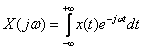
называют прямым преобразованием Фурье. Функция угловой частоты 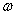 –
– 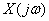 называется Фурье-изображением или частотным спектром функции
называется Фурье-изображением или частотным спектром функции  . Спектр характеризует соотношение амплитуд и фаз бесконечного множества бесконечно малых синусоидальных компонент, составляющих в сумме непериодический сигнал
. Спектр характеризует соотношение амплитуд и фаз бесконечного множества бесконечно малых синусоидальных компонент, составляющих в сумме непериодический сигнал  . Операция преобразования Фурье математически записывается следующим образом:
. Операция преобразования Фурье математически записывается следующим образом:
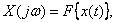
где 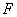 - символ прямого преобразования Фурье.
- символ прямого преобразования Фурье.
Спектры в теории автоматического управления представляют графически, изображая отдельно их действительную и мнимую части:

На рис. 1 представлено типичное изображение спектра непериодического сигнала.

Рис. 1
Отметим следующие особенности спектра непериодической функции  :
:
1. Спектр непериодической функции времени непрерывен;
2. Область допустимых значений аргумента спектра
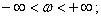
3. Действительная часть спектра – четная функция частоты, мнимая часть спектра – нечетная функция, что позволяет использовать одну половину спектра
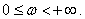
Преобразование Фурье обратимо, то есть, зная Фурье-изображение, можно определить исходную функцию – оригинал. Соотношение обратного преобразования Фурье имеет следующий вид:

или в сокращенной записи  , где
, где 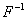 - символ обратного преобразования Фурье. Заметим, что временная функция имеет преобразование Фурье тогда и только тогда, когда:
- символ обратного преобразования Фурье. Заметим, что временная функция имеет преобразование Фурье тогда и только тогда, когда:
· функция однозначна, содержит конечное число максимумов, минимумов и разрывов;
· функция абсолютно интегрируема, то есть

Обратное преобразование Фурье возможно только в том случае, если все полюсы 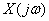 - левые.
- левые.
Рассмотрим примеры определения спектра временных функций.
Пример:
Найдем частотный спектр дельта-функции.
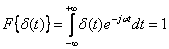 ,
,
так как при 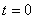
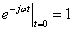 ,
,
а при 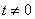
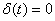 и
и
 .
.
В итоге, 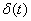 имеет единичный, равномерный и не зависящий от частоты действительный спектр, а мнимая часть спектра будет равна нулю (см. рис.2).
имеет единичный, равномерный и не зависящий от частоты действительный спектр, а мнимая часть спектра будет равна нулю (см. рис.2).
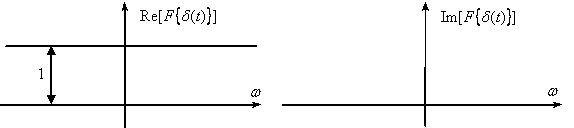
Рис. 2
Пример:
Найдем частотный спектр единичной ступенчатой функции.
Для этой функции не выполняется требование абсолютной интегрируемости, так как
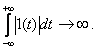
Поэтому 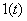 Фурье-изображения не имеет.
Фурье-изображения не имеет.
Преобразование Лапласа
Соотношение

называют прямым преобразованием Лапласа. Комплексная переменная 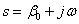 называется оператором Лапласа, где
называется оператором Лапласа, где 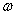 - угловая частота,
- угловая частота, 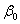 - некоторое положительное постоянное число. Функция комплексной переменной
- некоторое положительное постоянное число. Функция комплексной переменной 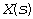 называется изображением сигнала
называется изображением сигнала  по Лапласу. Операция определения изображения по оригиналу сокращенно записывается -
по Лапласу. Операция определения изображения по оригиналу сокращенно записывается - 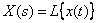 , где
, где  - символ прямого преобразования Лапласа.
- символ прямого преобразования Лапласа.
Преобразование Лапласа обратимо, то есть, зная изображение по Лапласу, можно определить оригинал, используя соотношение обратного преобразования

или 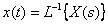 , где
, где 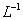 - символ обратного преобразования Лапласа.
- символ обратного преобразования Лапласа.
Отметим, что преобразование Лапласа изображает исходную функцию лишь при  , а поведение исходной функции при
, а поведение исходной функции при 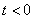 никак не сказывается на изображении. Класс функций, преобразуемых по Лапласу, значительно шире класса функций, преобразуемых по Фурье. Практически любые функции времени в ТАУ имеют преобразование Лапласа.
никак не сказывается на изображении. Класс функций, преобразуемых по Лапласу, значительно шире класса функций, преобразуемых по Фурье. Практически любые функции времени в ТАУ имеют преобразование Лапласа.
Получим изображения по Лапласу для импульсных функций.
 ,
,
так как 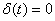 при
при 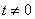 ,
,
 , и
, и 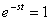 при
при 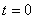 .
.
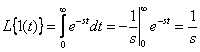 .
.
На практике для выполнения прямого и обратного преобразований Лапласа используются таблицы преобразований, фрагмент которой показан в табл. 1.
Таблица 1.

| 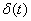
| 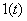
| 
| 
| 
| 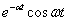
| 
|

| 1 | 
| 
| 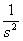
| 
| 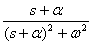
| 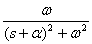
|
Таблицы преобразования Лапласа могут быть использованы для определения Фурье-изображений таких абсолютно интегрируемых функций, которые равны 0 при 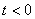 . Для получения Фурье-изображений в этом случае достаточно положить в изображении по Лапласу
. Для получения Фурье-изображений в этом случае достаточно положить в изображении по Лапласу 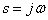 . В общем виде это выглядит как
. В общем виде это выглядит как
 ,
,
если  при
при 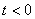 и
и 
Рассмотрим формулировки основных теорем преобразования Лапласа, которые широко используются в ТАУ.
1. Теорема линейности. Любое линейное соотношение между функциями времени справедливо и для изображений по Лапласу этих функций;
 ;
;
2. Теорема о дифференцировании оригинала.
Если 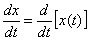 и
и 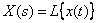 , то
, то 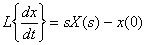 ,
,
где 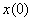 - начальное значение оригинала.
- начальное значение оригинала.
Дифференцирование 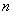 степени оригинала по времени при нулевых начальных условиях соответствует умножению изображения на
степени оригинала по времени при нулевых начальных условиях соответствует умножению изображения на 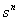 .
.
3. Теорема об интегрировании оригинала.
 ;
;
Замечание
В области изображений по Лапласу сложные операции дифференцирования и интегрирования сводятся к операциям умножения и деления на  , что позволяет переходить от дифференциальных и интегральных уравнений к алгебраическим. Это является главным достоинством преобразования Лапласа как математического аппарата теории автоматического управления.
, что позволяет переходить от дифференциальных и интегральных уравнений к алгебраическим. Это является главным достоинством преобразования Лапласа как математического аппарата теории автоматического управления.
Для нахождения оригинала функции по ее изображению используют обратное преобразование Лапласа. Функцию изображения необходимо представить в форме Хэвисайта, воспользовавшись необходимой формулой разложения дробно-рациональной функции. Полученную сумму простейших дробей подвергают обратному преобразованию Лапласа. Для этого можно воспользоваться таблицами преобразования Лапласа, которые определяют изображения многих временных функций. Фрагмент таблицы преобразования Лапласа приведен в табл. 1. В тех случаях, когда имеются комплексно-сопряженные полюсы изображения, необходимо преобразовать соответствующие простейшие дроби к виду, удобному для использования таблицы преобразования Лапласа.
Пример
Определим оригинал  по изображению в виде дробно-рациональной функции
по изображению в виде дробно-рациональной функции
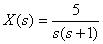 .
.
Используем разложение Хэвисайта для дробно-рациональной функции с одним нулевым полюсом. Тогда
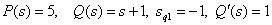 .
.
Коэффициенты разложения имеют вид
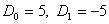 .
.
Изображение в форме Хэвисайта имеет вид
 .
.
Используем теорему о линейности и таблицу преобразований к каждому слагаемому, в результате получаем
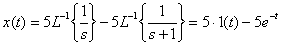 .
.
График функции оригинала имеет вид, показанный на рис. 3.
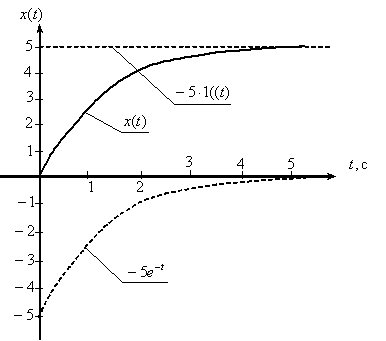
Рис. 3
Кратко поясним алгоритм решения дифференциальных уравнений операторным методом на примере решения дифференциального уравнения 2 порядка в общем виде
 ,
,
где 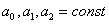 ,
, 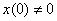 ,
, 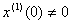 .
.
Применим теорему о дифференцировании для нахождения изображений производных
 ,
, 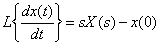 .
.
Пусть 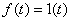 , тогда
, тогда
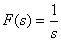 .
.
Получим операторное уравнение, используя теорему линейности
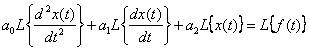 ,
,
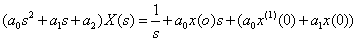 .
.
Решаем уравнение относительно  ,
,
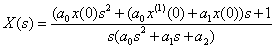 .
.
Найдем  , используя переход к форме Хэвисайта (разложение Хэвисайта)
, используя переход к форме Хэвисайта (разложение Хэвисайта)
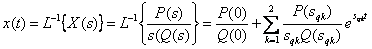 ,
,
где 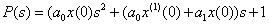 ,
,  .
.
Особо следует обратить внимание на получение изображения производной ступенчатой единичной функции 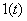 , которая определяется следующим образом:
, которая определяется следующим образом:
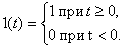
Если использовать
 ,
,
то получается ошибочное решение, поэтому следует использовать называемые "левые" начальные условия
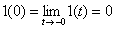 .
.
Справедливость этого можно легко проверить подстановкой решения в исходное дифференциальное уравнение.
Контрольные вопросы и задачи
1. Какие ограничения накладываются на прямое и обратное преобразование Фурье?
2. Как с помощью таблиц преобразования Лапласа получить частотный спектр реального сигнала – непериодической функции времени?
3. Если изображение по Лапласу имеет вид дробно-рациональной функции, в какой форме ее удобнее представлять для получения оригинала, в форме Боде или в форме Хэвисайта?
4. Определите оригинал следующего изображения по Лапласу
 .
.
Ответ:
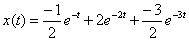 .
.
5. Определите оригинал следующего изображения по Лапласу
 .
.
Ответ:
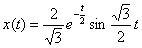 .
.
6. Найдите  , решив дифференциальное уравнение
, решив дифференциальное уравнение
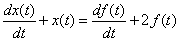 ,
,
где 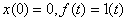 .
.
Ответ:
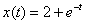 .
.
7. Найдите  , решив дифференциальное уравнение
, решив дифференциальное уравнение
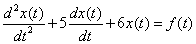 ,
,
где 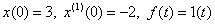 .
.
Ответ:
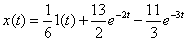 .
.
Лекция 6 Понятие линейного динамического звена
САУ удобно представлять для анализа и при синтезе в виде взаимосвязанной совокупности отдельных элементов – динамических звеньев.
Под динамическим звеном понимают в общем случае абстрактное устройство, имеющее вход и выход, и для которого задано уравнение, связывающее сигналы на входе и выходе, как это показано на рис. 1.
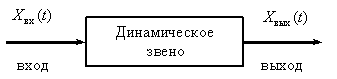
Рис. 1
Подробное изучение свойств реальных объектов управления и систем автоматического управления приводит к описанию динамических звеньев в виде нелинейных дифференциальных уравнений. Но во многих случаях их можно линеаризовать, то есть заменить нелинейные уравнения линейными, приближенно описывающими процессы в системах. Тем самым осуществляется декомпозиция задач анализа и синтеза систем, то есть первоначально используют линейное представление, а затем осуществляют учет вносимых нелинейностями особенностей. Такому подходу способствует то, что, в большинстве случаев, нормально функционирующая система работает в режиме малых отклонений, при которых нелинейности не проявляются. В дальнейшем мы будем рассматривать преимущественно аппарат изучения линейных систем, а особенности систем других классов: нелинейных, импульсных, цифровых и стохастических, будут излагаться позднее в других учебных дисциплинах.
Если уравнение, связывающее сигналы 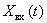 и
и 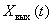 , линейно, то говорят о линейном динамическом звене
, линейно, то говорят о линейном динамическом звене
Уравнение линейного динамического звена имеет следующий общий вид:
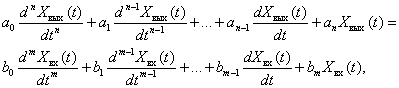
| (1) |
где 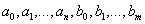 - постоянные коэффициенты,
- постоянные коэффициенты, 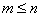 .
.
Использовать такое описание динамического звена в задачах анализа и синтеза систем и объектов управления не рационально, поэтому существуют и иные формы описания и представления динамических звеньев и систем в целом.
Передаточная функция
Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу
 .
.
Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов
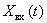
| (2) |
Преобразуем уравнение (2) к следующему виду
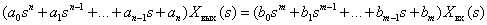
| (3) |
Получим из (3) отношение изображений выходного и входного сигналов

| (4) |
Отношение (4) не зависит от изображений сигналов, определяется только параметрами самого динамического звена (  ), имеет вид дробно-рациональной функции.
), имеет вид дробно-рациональной функции.
Отношение изображений выходного и входного сигналов называют передаточной функцией динамического звена
 .
.
Уравнение вида
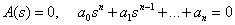 ,
,
называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции – это характеристический полином дифференциального уравнения, описывающего динамическое звено.
Пример
Определим передаточную функцию динамического звена по его принципиальной электрической схеме

Рис. 2
Решение:
По второму закону Кирхгоффа запишем уравнения описывающие схему
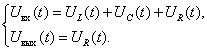
С учетом того, что
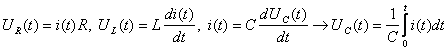 ,
,
получаем
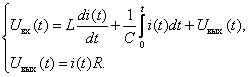
Получим операторные уравнения
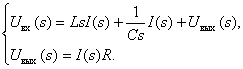
Из второго уравнения выразим значение изображения тока
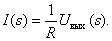
Подставим полученное выражение в первое уравнение системы
 .
.
В итоге получаем искомую передаточную функцию
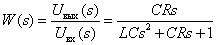 .
.
Структурная схема
Графически передаточные функции динамического звена представляют в следующем виде:
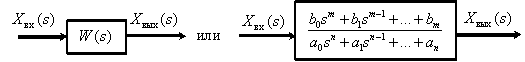
Рис. 3
Если известно изображение входного сигнала и передаточная функция динамического звена, всегда можно найти изображение выходного сигнала при нулевых начальных условиях
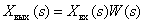 .(5)
.(5)
В общем случае САУ состоит из множества динамических звеньев, сигналы с выходов звеньев могут суммироваться или вычитаться, суммироваться с внешними для САУ сигналами. Суммирование и вычитание изображений сигналов могут быть представлено графически с помощью суммирующих звеньев:
1. 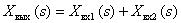
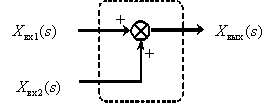
2. 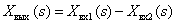

Показанная выше неоднозначность графического представления вычитания изображений на суммирующем элементе связана с различием в стандартах разных стран.
Используя графическое представление передаточных функций звеньев и суммирующие звенья, можно в графической форме представить операторные уравнения, описывающие САУ. Такое графическое представление операторных уравнений в ТАУ называют структурной схемой.
Пример
По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.

Решение:
Получим систему операторных уравнений, подвергнув исходную систему дифференциальных уравнений преобразованию Лапласа и заменив оригиналы изображениями,
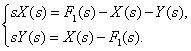
Из первого уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим
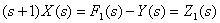 .
.
Тогда передаточная функция этого звена имеет вид
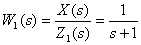 ,
,
а выражение 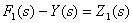 описывает суммирующее звено
описывает суммирующее звено 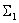 . Таким образом, получены два фрагмента структурной схемы
. Таким образом, получены два фрагмента структурной схемы
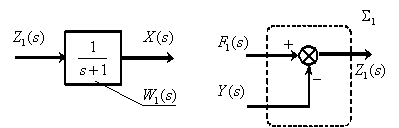
Из второго уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим, вводя обозначение,
 .
.
Тогда передаточная функция этого звена имеет вид
 ,
,
а выражение  описывает суммирующее звено
описывает суммирующее звено 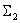 . Таким образом, получены еще два фрагмента структурной схемы
. Таким образом, получены еще два фрагмента структурной схемы
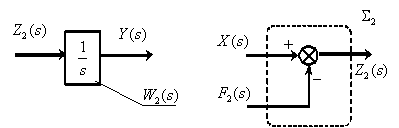
Соединим все фрагменты структурной схемы объекта управления, объединяя одноименные сигналы, либо разветвляя их с помощью точек ветвления , показанных на схеме. В результате получим
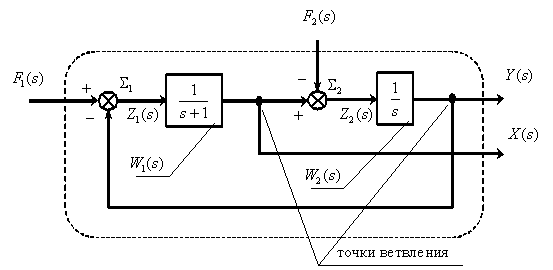
Временные характеристики динамического звена
Временной или импульсной характеристикой динамического звена называют реакцию звена на 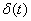 , обозначая ее как
, обозначая ее как 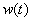 . При этом схема эксперимента имеет вид –
. При этом схема эксперимента имеет вид –
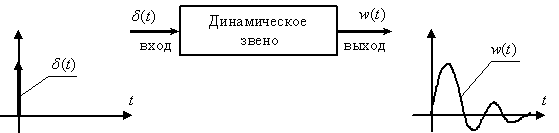
Рис. 4
Выясним, что представляет собой временная характеристика, то есть почему ее называют характеристикой динамического звена?
Для этого рассмотрим динамическое звено с передаточной функцией 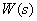
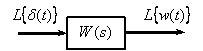
Рис. 5
В этом случае, в соответствии с (5), имеем
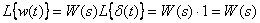 .
.
Таким образом
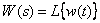
Получаем, что передаточная функция звена – это изображение по Лапласу импульсной характеристики динамического звена. В свою очередь, импульсная характеристика может быть определена по передаточной функции
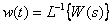 ,
,
при использовании разложения в форму Хэвисайта и обратное преобразование Лапласа.
Знание импульсной характеристики позволяет определить реакцию динамического звена на сигнал любой формы.
Для динамического звена с передаточной функцией 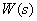 преобразуем (5), используя теорему об умножении изображений преобразования Лапласа,
преобразуем (5), используя теорему об умножении изображений преобразования Лапласа,
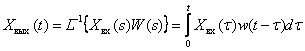 ,
,
а если легко получить 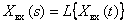 , тогда
, тогда
 .
.
Переходной характеристикой или переходной функцией динамического звена называют реакцию динамического звена на 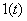 , обозначая ее как
, обозначая ее как 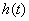 . При этом схема эксперимента имеет вид –
. При этом схема эксперимента имеет вид –

Рис. 6
Для анализа переходной характеристики рассмотрим динамическое звено с передаточной функцией 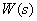

Рис. 7
В этом случае, в соответствии с (5), имеем
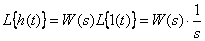 .
.
По теореме об интегрировании оригинала имеем
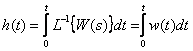
Переходная функция является интегралом по времени от импульсной характеристике и наоборот
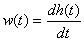 .
.
Переходная характеристика динамического звена может быть определена по передаточной функции
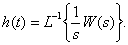
Контрольные вопросы и задачи
1. Что такое линейное динамическое звено?
2. Как определить передаточную функцию линейного динамического звена?
3. Перечислите основные элементы структурных схем систем управления.
4. Как определить по передаточной функции динамического звена его временные характеристики: импульсную и переходную?
5. Как по переходной характеристике определить импульсную характеристику динамического звена?
6. Определите передаточную функцию динамического звена по его принципиальной электрической схеме
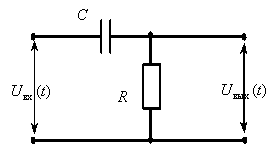
Ответ:
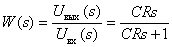 .
.
7. Определите передаточную функцию динамического звена по его принципиальной электрической схеме
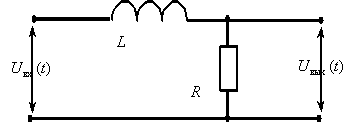
Ответ:
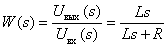 .
.
8. По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.

Ответ:

Лекция 7 Частотные характеристики динамического звена
Частотной характеристикой динамического звена называют функцию комплексного аргумента 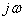 , полученную путем формальной замены
, полученную путем формальной замены 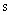 на
на 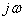 в выражении передаточной функции
в выражении передаточной функции
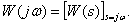
Получим связь частотной характеристики с известными понятиями. Для этого рассмотрим динамическое звено с передаточной функцией 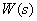 и сигналами
и сигналами 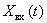 ,
, 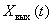 . Пусть
. Пусть 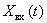 ,
, 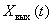 – абсолютно интегрируемые функции и равны нулю при
– абсолютно интегрируемые функции и равны нулю при 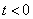 . Тогда частотные спектры этих сигналов (преобразование Фурье) этих функций можно определить следующим образом –
. Тогда частотные спектры этих сигналов (преобразование Фурье) этих функций можно определить следующим образом –
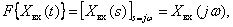
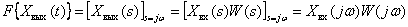 .
.
Получим отношение спектров
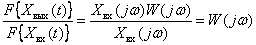 .
.
Таким образом, частотную характеристику динамического звена можно определить как отношение спектра (преобразования Фурье) выходного сигнала к спектру входного сигнала.
Знание частотной характеристики звена позволяет определить выходной спектр по входному
 .
.
Рассмотрим динамическое звено –
Рис. 1
Получим спектр выходного сигнала – импульсной характеристики
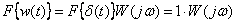 .
.
Тогда имеем
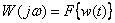 ,
,
то есть преобразование Фурье от импульсной характеристики равно частотной характеристике динамического звена.
Частотная функция характеристика как функция комплексного аргумента может быть представлена в следующем виде –
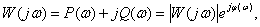
где 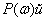 – действительная (вещественная) часть
– действительная (вещественная) часть 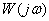 ,
,
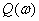 – мнимая часть
– мнимая часть 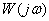 ,
,
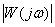 – модуль (амплитуда)
– модуль (амплитуда) 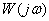 ,
,
 – фаза аргумент
– фаза аргумент 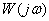 .
.
Амплитуда, фаза, действительная и мнимая части частотной характеристики являются функциями частоты, поэтому частотная характеристика используется и графически представляется в виде амплитудно-фазовой, действительной, мнимой, амплитудной и фазовой частотных характеристик.
В теории автоматического управления рассматривают и используют следующие частотные характеристики динамических звеньев:
1. Амплитудно-частотная характеристика (АЧХ) –
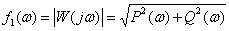 .
.
2. Фазочастотная характеристика (ФЧХ) –
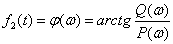 .
.
3. Вещественная частотная характеристика (ВЧХ) –
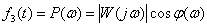 .
.
4. Мнимая частотная характеристика (МЧХ) –
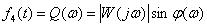 .
.
5. Амплитудно-фазовая частотная характеристика (АФЧХ), которая определяется как годограф (след движения конца) вектора 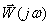 , построенный на комплексной плоскости при изменении частоты от 0 до
, построенный на комплексной плоскости при изменении частоты от 0 до 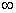 .
.
На рис. 2 покажем частотные характеристики некоторого динамического звена.
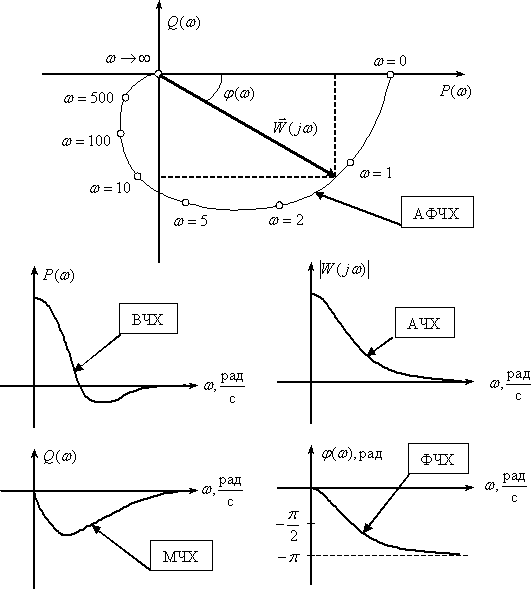
Рис. 2
Для выяснения физического смысла частотной характеристики рассмотрим динамическое звено с передаточной функцией 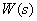 и импульсной характеристикой
и импульсной характеристикой 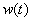 , на вход которого подаем гармонический сигнал
, на вход которого подаем гармонический сигнал 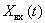 .
.

Рис. 3
Вспомним, что решение линейного дифференциального уравнения динамического звена, в рамках классического метода, состоит из двух составляющих – свободной и установившейся.
Установившаяся составляющая в случае гармонической функции времени, стоящей в правой части уравнения, так же является гармонической функцией времени. Поэтом установившийся сигнал на выходе динамического звена можно описать следующим выражением
 .
.
Сигнал на выходе звена определим с помощью теоремы об умножении изображений

В результате получаем
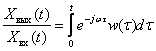 .
.
Для перехода к установившемуся режиму полагаем  , тогда получаем
, тогда получаем
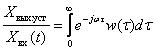 .
.
Но, с другой стороны, имеем по определению прямого преобразования Фурье
 .
.
Поэтому
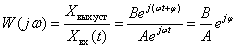 .
.
Отсюда следует простой алгоритм экспериментального определения частотной характеристики линейного динамического звена, объекта или системы управления для конкретной частоты  :
:
1. Подать на вход объекта синусоидальный сигнал частоты  и постоянной амплитуды.
и постоянной амплитуды.
2. Дождаться затухания свободной составляющей переходного процесса.
3. Измерить амплитуду выходного сигнала и сдвиг его по фазе относительно входного сигнала.
4. Отношение амплитуды выходного установившегося сигнала к амплитуде входного сигнала определит модуль частотной характеристики при частоте  .
.
5. Сдвиг фазы выходного сигнала относительно входного сигнала определит угол (аргумент) частотной характеристики при частоте  .
.
Применяя данный алгоритм для частот от нуля до бесконечности, можно экспериментальным путем определить частотную характеристику конкретного устройства.
Физический смысл частотной характеристики: показывает, во сколько раз изменяет динамическое звено (устройство), работающее в установившемся режиме, амплитуду входной синусоиды частоты 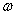 , и на какой угол сдвигает входную синусоиду по фазе.
, и на какой угол сдвигает входную синусоиду по фазе.
Контрольные вопросы и задачи
1. Как определить частотную характеристику динамического звена, если известна его передаточная функция?
2. Какие виды частотных характеристик вы знаете?
3. Как определить амплитуду и аргумент частотной характеристики?
4. Перечислите основные этапы экспериментального снятия частотной характеристики устройства.
5. Поясните физический смысл частотной характеристики линейного динамического звена.
6. Определите выражение частотной характеристики по заданной передаточной функции
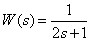 .
.
Ответ: 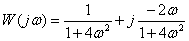 .
.
7. Определите выражение частотной характеристики по заданной передаточной функции
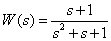 .
.
Ответ: 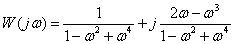 .
.
8. Определите выражения амплитудной и фазовой частотных характеристик для динамического звена с передаточной функцией –
 .
.
Ответ: 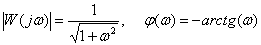 .
.
9. На вход динамического звена с передаточной функцией
 ,
,
поступает гармонический сигнал постоянной амплитуды с частотой
 .
.
На какой угол будет смещен выходной сигнал в установившемся режиме?
Ответ: 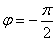
Лекция 8 Элементарные (типовые) динамические звенья
Любая линейная САУ может быть представлена в виде передаточной функции в форме Боде
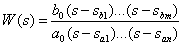 ,(1)
,(1)
где 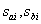 могут быть или действительными или комплексно-сопряженными. Рассмотрим отдельно каждый случай.
могут быть или действительными или комплексно-сопряженными. Рассмотрим отдельно каждый случай.
Действительные нули и полюсы
Преобразуем сомножители из (1), введя обозначения
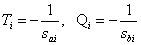 ,
,
в итоге имеем сомножители следующего вида –
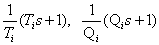 (2)
(2)
Комплексно-сопряженные нули и полюсы
В этом случае имеем корни вида –
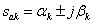 ,
,
и соответствующие им сомножители
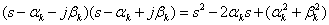 .
.
Введем обозначения –
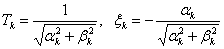 ,
,
получим сомножители следующего вида
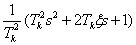 ,(3)
,(3)
в числителе и знаменателе передаточной функции.
Тогда (1) с учетом (2) и (3) можно записать в следующем виде
в итоге имеем сомножители следующего вида –
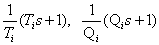 .(2)
.(2)
Комплексно-сопряженные нули и полюсы
В этом случае имеем корни вида –
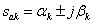 ,
,
и соответствующие им сомножители
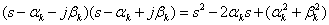 .
.
Введем обозначения –
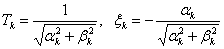 ,
,
получим сомножители следующего вида
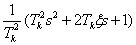 ,(3)
,(3)
в числителе и знаменателе передаточной функции.
Тогда (1) с учетом (2) и (3) можно записать в следующем виде
 ,(4)
,(4)
где
 .
.
Из (4) следует, с учетом правила эквивалентного преобразования структурных схем, что линейная САУ может быть представлена в виде последовательного соединения элементарных динамических звеньев 1-го и 2-го порядка с передаточными функциями следующего вида
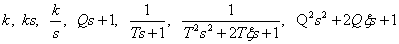 .(5)
.(5)
Кроме того, передаточную функцию САУ можно представить в форме Хэвисайта –
 .
.
Из чего следует, что САУ можно представить в виде параллельно соединенных звеньев с передаточными функциями вида (5). Кроме того, передаточными функциями 1-го и 2-го порядка описываются многие функциональные компоненты систем управления
Такие динамические звенья называют элементарными или типовыми звеньями, изучение их свойств и характеристик многое дает при синтезе и анализе реальных и сложных систем.
К типовым звеньям относят следующие динамические звенья:
1. Безынерционное (масштабирующее, пропорциональное) звено
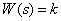 .
.
2. Дифференцирующее звено
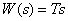 .
.
3. Интегрирующее звено
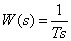 .
.
4. Апериодическое звено
 .
.
5. Колебательное звено
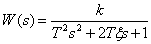 .
.
6. Форсирующие звенья
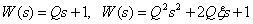 .
.
Замечание
Следующие звенья не являются элементарными в полном смысле этого слова, но их часто относят к типовым в силу их широкого распространения.
7. Реальное дифференцирующее звено
 .
.
8. Интегральное звено с замедлением
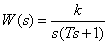 .
.
9. Пропорционально-интегральное звено
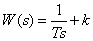 .
.
Характеристики (временные и частотные) типовых звеньев могут быть получены аналитически по их передаточным функциям, при этом удобно использовать сводную диаграмму, показывающую взаимосвязь математических моделей динамических звеньев.

Рис. 1
Контрольные вопросы и задачи
1. Дайте определение типового динамического звена.
2. Почему типовые динамические звенья так подробно изучают?
3. Перечислите динамические звенья, которые относят к типовым (элементарным).
4. Как по передаточной функции определить импульсную характеристику динамического звена?
5. Как по передаточной функции определить переходную характеристику динамического звена?
6. Как по передаточной функции определить частотную характеристику динамического звена?
7. Какое типовое звено смещает гармонический сигнал любой частоты на угол 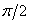 в сторону запаздывания?
в сторону запаздывания?
8. Какое типовое звено смещает гармонический сигнал любой частоты на угол 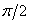 в сторону опережения?
в сторону опережения?
9. Какое типовое звено не изменяет фазу гармонического сигнала любой частоты?
Лекция 9 Правила эквивалентных преобразований структурных схем систем автоматического управления
Выше были рассмотрены математические модели отдельных динамических звеньев. САУ представляет собой систему, состоящую из функциональных элементов, каждый из которых может быть представлен в виде динамического звена. То есть САУ можно представить в виде совокупности динамических звеньев с известными математическими моделями. Рассмотрим структуру типичной САУ –
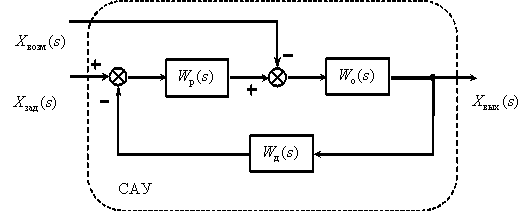
где 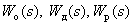 – передаточные функции соответственно объекта, датчика и регулятора,
– передаточные функции соответственно объекта, датчика и регулятора, 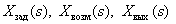 – изображения задающего, возмущающего и выходного сигналов.
– изображения задающего, возмущающего и выходного сигналов.
В процессе анализа и синтеза САУ необходимо получать передаточные функции САУ, которые связывают выходную переменную с заданием и возмущением в САУ, по известным структурной схеме и передаточным функциям динамических звеньев, входящих в состав САУ.
Аналогичная задача возникает в том случае, когда известны частотные характеристики динамических звеньев, а необходимо определить частотные характеристики САУ, характеризующие связи между выходом и входом САУ.
Решением этих задач мы и займемся в дальнейшем.
Эта задача решается путем преобразования (сворачивания) структурной схемы к одному динамическому звену с искомой передаточной функцией на основе использования правил эквивалентных преобразований структурных схем и принципа суперпозиции (наложения).
Правила эквивалентных преобразований позволяют найти необходимую передаточную функцию САУ, свернув структурную схему к одному динамическому звену с искомой передаточной функцией.
Рассмотрим правила эквивалентных преобразований, не изменяющих свойств систем и необходимых для нахождения передаточной функции:
1. Последовательное соединение динамических звеньев.
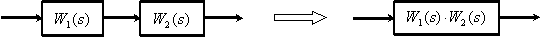
2. Параллельное соединение динамических звеньев.
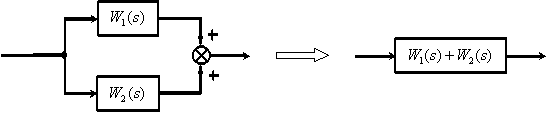
3. Замкнутый контур с отрицательной обратной связью.
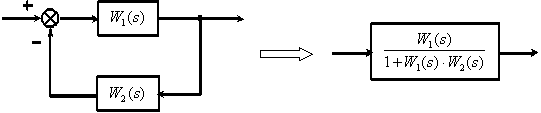
4. Замкнутый контур с положительной обратной связью.
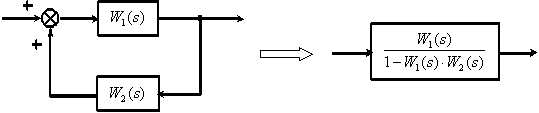
5. Перенос точки ветвления через динамическое звено.
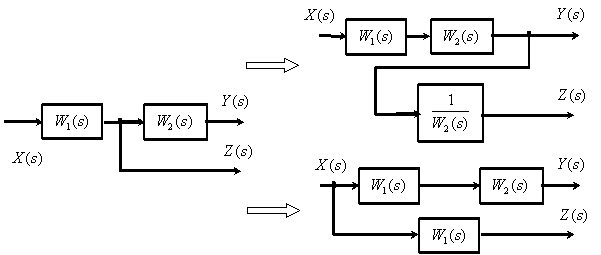
Лекция 10 Ориентированные графы систем автоматического управления
Математическую модель САУ можно наглядно представить с помощью ориентированных графов (орграфов).
Орграфы используются в сложных САУ, особенно при управлении и автоматизации технологических процессов в промышленности, когда описание в виде структурных схем становится громоздким и сложным для восприятия. Рассмотрим простейший орграф динамического звена САУ.
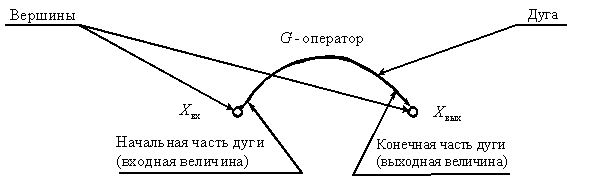
Рис. 1
Орграфом САУ является графическое представление САУ в виде совокупности вершин, соответствующих переменным, и дуг, соединяющих вершины.
Рассмотрим основные свойства орграфа:
1. Каждая дуга со стрелкой, указывающей направление распространения сигнала, изображает звено и характеризуется оператором изображаемого звена (передаточной функцией);
2. Каждой вершине, отмеченной кружком, ставится в соответствие одна из переменных САУ (изображение переменной по Лапласу);
3. Входная величина дуги равна переменной вершины, из которой эта дуга исходит;
4. Выходная величина дуги получается как результат преобразования оператором входной величины;
5. Если к вершине подходят несколько дуг, то соответствующая вершине переменная равна сумме выходных величин этих дуг (аналог суммирующего звена структурных схем);
6. Если из вершины исходит несколько дуг, то входные величины всех этих дуг одинаковы (аналог точки ветвления в структурных схемах).
Ориентированный граф (орграф) можно построить по структурной схеме и наоборот. При построении орграфа по структурной схеме необходимо придерживаться следующих правил:
1. Модифицируют структурную схему так, чтобы в сумматорах все переменные складывались с положительным знаком, отрицательные знаки вносятся в передаточные функции соответствующих звеньев;
2. Каждый сумматор структурной схемы заменяется вершиной, которой ставится в соответствие выходная переменная сумматора;
3. Каждое динамическое звено заменяется дугой с оператором, равным передаточной функции звена;
4. Каждой переменной, включая и входные воздействия, соответствует своя вершина.
Рассмотрим пример. На рис. 2 показана структурная исходная схема, на рис. 3 показан полученный орграф САУ.
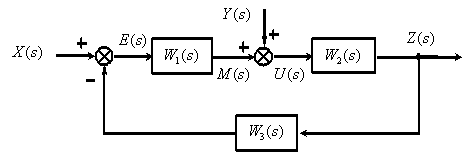
Рис. 2
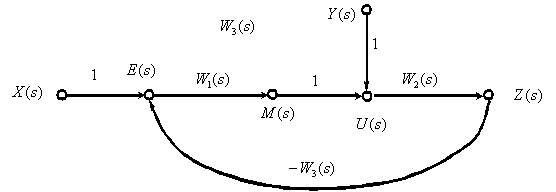
Рис. 3
Преобразовать орграф САУ можно, как и структурную схему, используя правила эквивалентных преобразований для орграфов, которые легко могут быть получены по аналогичным правилам для структурных схем.
5. Последовательное соединение динамических звеньев.

6. Параллельное соединение динамических звеньев.
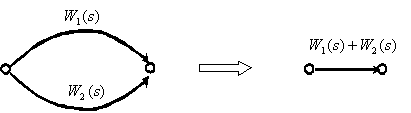
7. Замкнутый контур с отрицательной обратной связью.
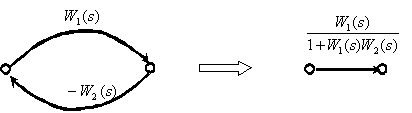
8. Замкнутый контур с положительной обратной связью.
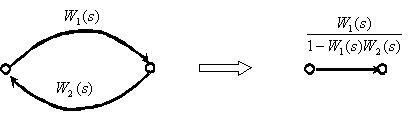
9. Перенос точки ветвления через динамическое звено.
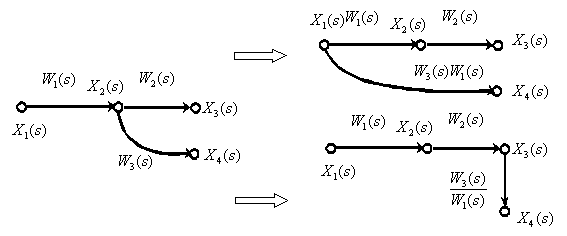
10. Перенос суммирующего звена через динамическое звено.
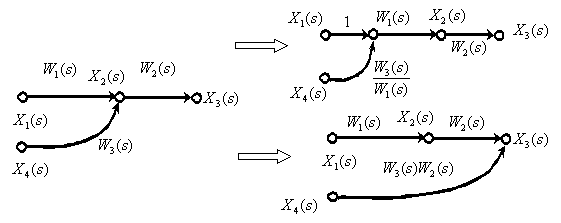
Использование формулы Мейсона для преобразования структурных схем и ориентированных графов
Когда структурная схема преобразована в орграф, для нахождения необходимой передаточной функции можно использовать формулу Мейсона (правило некасающихся контуров), которая позволяет получить передаточную функцию, связывающую переменные в сложных, многоконтурных САУ.
Рассмотрим общий вид формулы и поясним ее компоненты:
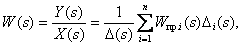
| (1) |
где  - передаточная функция
- передаточная функция 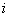 -го отдельного прямого пути от
-го отдельного прямого пути от 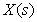 до
до  , вычисленная как произведение передаточных функций дуг, входящих в этот путь;
, вычисленная как произведение передаточных функций дуг, входящих в этот путь;
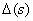 - определитель орграфа.
- определитель орграфа.
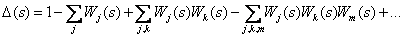
| (2) |
где 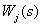 - передаточная функция
- передаточная функция 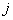 -го замкнутого контура, вычисленная как произведение передаточных функций дуг, входящих в этот контур;
-го замкнутого контура, вычисленная как произведение передаточных функций дуг, входящих в этот контур;
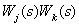 - произведение передаточных функций пары (
- произведение передаточных функций пары ( 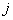 -го и
-го и  -го) замкнутых контуров, не касающихся ни дугами, ни вершинами, суммирование осуществляется по всем парам некасающихся контуров;
-го) замкнутых контуров, не касающихся ни дугами, ни вершинами, суммирование осуществляется по всем парам некасающихся контуров;
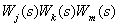 - произведение тройки (
- произведение тройки ( 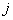 -го,
-го,  -го и
-го и 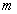 -го) некасающихся контуров, суммирование производится по всем тройкам не касающихся контуров.
-го) некасающихся контуров, суммирование производится по всем тройкам не касающихся контуров.
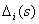 - определитель орграфа, полученного при удалении дуг и вершин
- определитель орграфа, полученного при удалении дуг и вершин 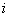 -го отдельного прямого пути, определяется по формуле (2).
-го отдельного прямого пути, определяется по формуле (2).
Поясним использование формулы Мейсона.
В начале выявляются все отдельные прямые пути между входной и выходной переменными, для которых необходимо определить передаточную функцию. Отдельным прямым путем считается такая последовательность дуг и вершин, которая соединяет вершины, соответствующие входному и выходному сигналам. При этом отдельный прямой путь не должен пересекать в вершинах сам себя.
Далее выявляются все замкнутые контуры в орграфе САУ. Замкнутым считается такой контур, когда между двумя вершинами имеется как прямая, так и обратная связь. Передаточная функция замкнутого контура определяется как произведение передаточных функций всех дуг, входящих в контур с учетом знаков.
После того как выявлены все замкнутые контуры орграфа, необходимо проанализировать – есть ли контуры, которые не касаются ни дугами, ни вершинами, есть ли пары, тройки и т. д. таких контуров.
На основании полученного формируется определитель орграфа по формуле (2).
Определители орграфов, полученных после изъятия 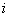 -х отдельных прямых путей, также формируются по формуле (2), при этом учитываются только те контуры, которые остаются после изъятия
-х отдельных прямых путей, также формируются по формуле (2), при этом учитываются только те контуры, которые остаются после изъятия 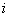 -го прямого пути. Если после изъятия прямого пути не остается ни одного замкнутого контура, определитель такого орграфа принимается равным единице.
-го прямого пути. Если после изъятия прямого пути не остается ни одного замкнутого контура, определитель такого орграфа принимается равным единице.
В качестве примера определим передаточную функцию между  и
и 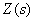 в структурной схеме САУ, показанной на рис. 4, полагая в соответствии с принципом суперпозиции
в структурной схеме САУ, показанной на рис. 4, полагая в соответствии с принципом суперпозиции 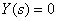 .
.
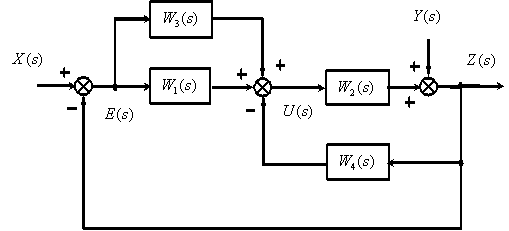
Рис. 4
Преобразуем структурную схему в ориентированный граф (рис. 5).
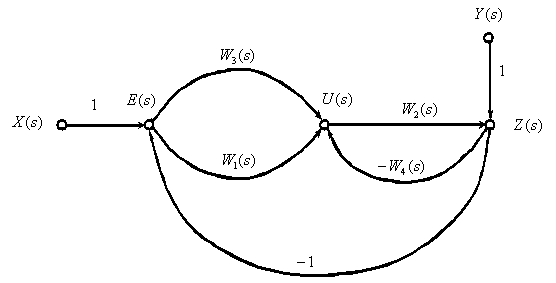
Рис. 5
Определим прямые пути:
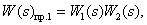
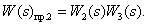
Определим замкнутые контуры:
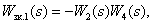
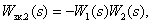
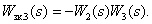
Все контуры имеют общую дугу 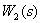 , поэтому некасающихся контуров нет. Определитель орграфа имеет вид
, поэтому некасающихся контуров нет. Определитель орграфа имеет вид
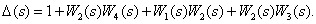
При изъятии 1-го или 2-го прямых путей в орграфе не сохраняется ни одного замкнутого контура, поэтому
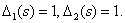
Передаточная функция имеет вид

Контрольные вопросы и задачи
1. Дайте определение орграфа динамического звена.
2. Поясните процедуру преобразования структурной схемы САУ в ориентированный граф.
3. Что называется отдельным прямым путем при использовании правила некасающихся контуров?
4. Какие замкнутые контуры называют некасающимися?
5. Определите передаточную функцию

по следующей структурной схеме
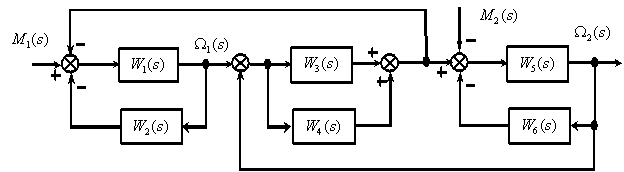
Ответ:
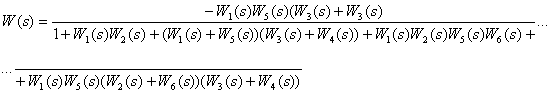 .
.
6. Определите передаточную функцию
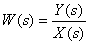
по следующей структурной схеме

Ответ:
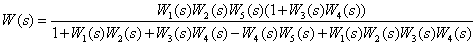 .
.
7. Определите передаточную функцию
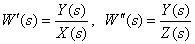
по следующей структурной схеме
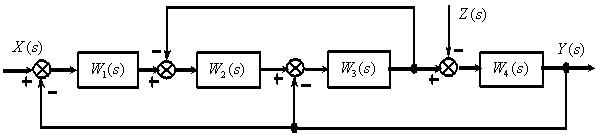
Ответ:
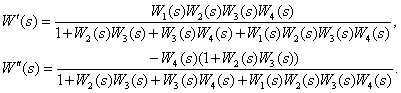 .
.
8. Определите передаточную функцию

по следующей структурной схеме
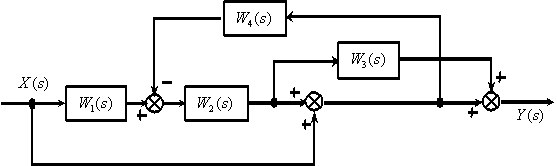
Ответ:
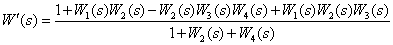 .
.
Лекция 11 Логарифмические частотные характеристики динамических звеньев
При рассмотрении и сравнение частотных характеристик амплитудных и фазочастотных для устройств различных видов возникает проблема их компактного представления, так как значения амплитуд и частот (см. рис. 1) существенно различаются друг от друга. Кроме того, и сама величина диапазона частот, в котором характеристики конкретного устройства представляют интерес, может быть весьма значительна, от долей герц до десятков мегагерц.

Рис. 1
Решение этой проблемы лежит в использовании логарифмических масштабов в частотных характеристиках.
Впервые обратились к логарифмическим масштабам в технике связи, так как там рассматриваются объекты, как с большими коэффициентами усиления, так и объекты которые характеризуются существенным затуханием сигналов.
В технике связи используют понятие коэффициента передачи по мощности для четырехполюсника, показанного на рис. 2,

Рис. 2
 .
.
Значительный диапазон изменения этого коэффициента и заставил использовать логарифмическое представление, логарифмический коэффициент передачи по мощности –
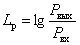
| (1) |
Логарифмический коэффициент усиления по мощности измеряют специальными единицами, которые носят название Белл (Б).
1 Белл соответствует усилению мощности в 10 раз.
Чаще используют единицу в десять раз меньшую – децибел (дБ).
 .
.
При определении логарифмического коэффициента в децибелах, выражение (1) принимает вид –
 .
.
Логарифмический коэффициент усиления можно выразить через отношение выходного и входного напряжений при одинаковых нагрузочных сопротивлениях 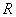
 .
.
Такое представление коэффициента усиления используют в теории автоматического управления для измерения амплитуды частотной характеристики в децибелах –

| (2) |
По оси частот в теории автоматического управления так же используют логарифмический масштаб на основе десятичного логарифма частоты.
При этом ось частот будет иметь следующий вид –
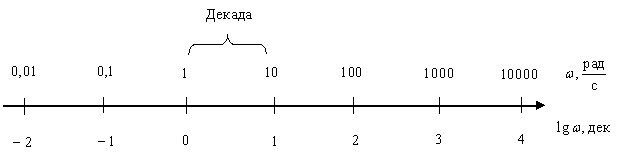
Рис. 3
Изменение частоты в десять раз называют декадой. Причем на оси частот, при ее логарифмическом масштабе, принято обозначать значения частоты в рад/с, иногда в герцах, особенно это принято в радиотехнике и в инженерной практике.
Особо отметим, что логарифмическая шкала не имеет нуля и может пересекаться вертикальной осью в любом месте, что особенно важно тем, что дает возможность рассматривать частотные свойства динамических звеньев и конкретных устройств в необходимом диапазоне изменения частот, где характеристика представляет интерес для исследователя.
Теперь дадим определение логарифмическим частотным характеристикам.
Логарифмической амплитудной частотной характеристикой (ЛАЧХ) динамического звена называют такое представление амплитудной частотной характеристики (АЧХ), в котором модуль (амплитуда) частотной характеристики выражен в децибелах, а частота – в логарифмическом масштабе.
Логарифмической фазовой частотной характеристикой (ЛФЧХ) динамического звена называют такое представление фазочастотной характеристики (ФЧХ) , в котором частота выражена в логарифмическом масштабе.
Довольно часто ЛАЧХ И ЛФЧХ строятся на одном графике, чтобы давать полное представление о свойствах объекта, покажем на рис. 4 примерный вид и оформление ЛАЧХ и ЛФЧХ некоторого инерционного объекта.

Контрольные вопросы и задачи
1. Дайте определение величине в 1 Белл.
2. Каким образом вычисляется логарифмический коэффициент усиления по мощности для четырехполюсников?
3. Что определяет понятие "декада" применительно к логарифмическим частотным характеристикам?
4. Дайте определение логарифмической амплитудной частотной характеристике.
5. Дайте определение логарифмической амплитудной частотной характеристике.
6. Перечислите основные достоинства логарифмических частотных характеристик по сравнению с обычными частотными характеристиками.
7. Передаточная функция звена –
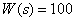 ,
,
как зависит от частоты ЛАЧХ этого звена? Определите ЛАЧХ этого звена.
Ответ:
ЛАЧХ не зависит от частоты,
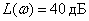 .
.
8. Передаточная функция звена –
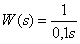 ,
,
определите значение ЛАЧХ этого звена при частоте 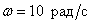 .
.
Ответ:
 .
.
9. Передаточная функция звена –
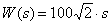 ,
,
определите наклон ЛАЧХ этого звена.
Ответ:
Наклон ЛАЧХ этого звена составляет 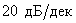 .
.
10. Передаточная функция объекта имеет вид –
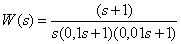 ,
,
Постройте асимптотическую ЛАЧХ объекта?
Ответ:
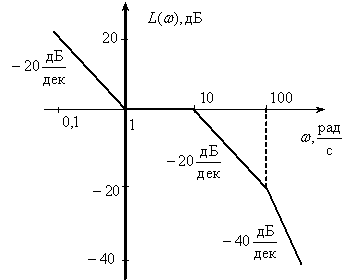
Лекция 12 Структурные матричные схемы и передаточные матрицы
Матричные структурные схемы
Матричные структурные схемы являются по сути компактным графическим представлением классической структурной схемы многомерного объекта или системы управления. Они основываются на операторной форме представления уравнений, на замене реальных сигналов их изображениями по Лапласу.
Используя несколько уровней представления схем, различающихся степенью агрегатирования (объединения) связей и элементов системы.
Рассмотрим различные уровни представления матричных структурных схем на примере некоторой обобщенной структуры многомерной системы автоматического управления.
I уровень
На рис. 3 показаны  – векторы изображений переменных,
– векторы изображений переменных,
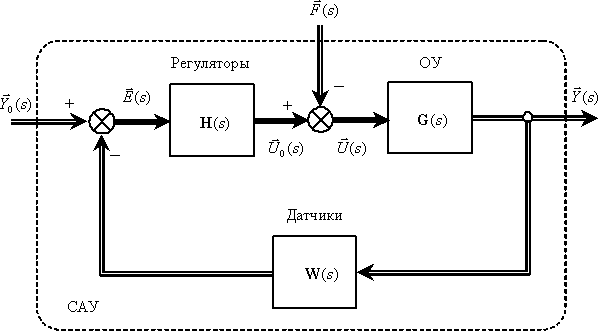
Рис. 1
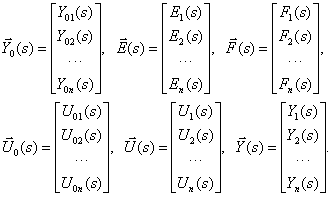 ,
,
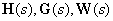 – матрицы передаточных функций,
– матрицы передаточных функций,
 ,
,
 ,
,
 .
.
На показанной на рис. 1 матричной структурной схеме суммирующие элементы, матричные звенья и точки ветвления выполняют те же функции, что и на обычных структурных схемах. Поэтому в соответствии со схемой можно записать систему матричных уравнений –
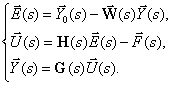
II уровень
Рассмотри второй уровень, полагая для матричной структурной схемы 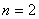 .
.
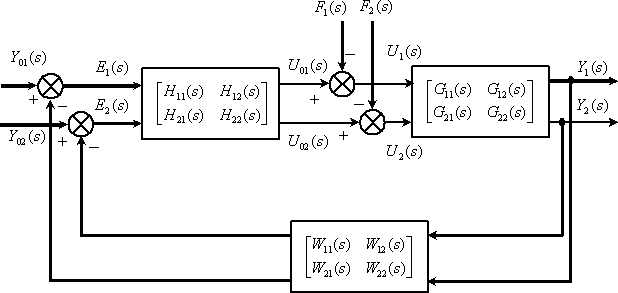
Рис. 2
Рассмотрим на этом уровне ОУ, описываемый матрицей 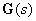
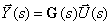
| (1) |
Перейдем от матричных уравнений к скалярным –
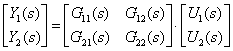 ,
,
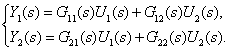
| (2) |
Из последнего выражения видно, что передаточная функция 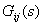 в соответствии с принципом суперпозиции является передаточной функцией между
в соответствии с принципом суперпозиции является передаточной функцией между 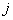 -м входом и
-м входом и 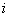 -м выходом, при отсутствии сигналов на всех входах, кроме
-м выходом, при отсутствии сигналов на всех входах, кроме 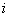 -го.
-го.
III уровень
Рассмотри третий уровень матричной структурной только для объекта управления. На основании полученной для объекта системы операторных уравнений (2) можно изобразить структурную схему объекта управления.
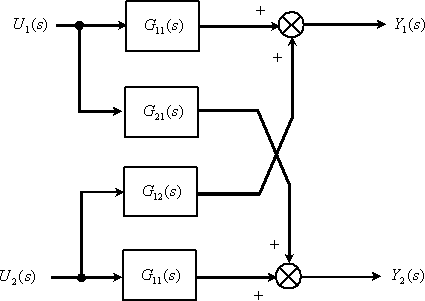
Рис. 3
Из предложенного примера уровней сложности матричной структурной схемы видно, что представление даже не очень сложных многомерных систем управления в виде схем III уровня, то есть в виде классических структурных схем, приводит к громоздкому графическому представлению, не отражающему характерных связей и функциональных элементов системы.
Передаточные матрицы
Передаточные или эквивалентные матрицы относятся к моделям типа "вход-выход" и представляют собой матрицы, связывающие вход и выход многомерной системы. На рис. 4 показана многомерная система.
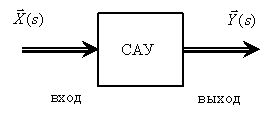
Рис. 4
Матричное операторное уравнение описывающее систему имеет вид –
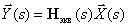 ,
,
где 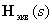 – передаточная или матрица системы, компонентами, которой будут передаточные функции, связывающие компоненты векторов входа и выхода системы.
– передаточная или матрица системы, компонентами, которой будут передаточные функции, связывающие компоненты векторов входа и выхода системы.
Аналогами эквивалентных матриц в одномерных системах являются передаточные функции, связывающие вход и выход объекта или системы. Матрицы 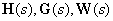 из рассмотренной выше матричной структурной схемы (см. рис. 1) являются, по сути, передаточными матрицами многомерных функциональных элементов системы.
из рассмотренной выше матричной структурной схемы (см. рис. 1) являются, по сути, передаточными матрицами многомерных функциональных элементов системы.
Эквивалентные матрицы многомерных систем могут быть получены двумя способами.
1. Определяются передаточные функции, связывающие соответствующие входы и выходы системы. То есть матрица определяется по ее компонентам. Компоненты определяются известными способами в соответствии с принципом суперпозиции.
2. Передаточные матрицы определяются в результате эквивалентных преобразований матричных структурных схем или по матричным операторным уравнениям. Преобразование матричных структурных схем осуществляется в соответствии с правилами эквивалентных преобразований обычных структурных схем, необходимо лишь учитывать специфику операций с векторами и матрицами (не соблюдение коммутативного закона, замена деления умножением на обратную матрицу, понятие единичной и нулевой матрицы и т. п.).
В качестве примера найдем передаточную матрицу, связывающую вход и выход рассматриваемой выше системы (рис. 1), при этом полагаем в соответствии с принципом суперпозиции, что сигнал возмущения отсутствует ( 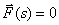 ). Тогда структурная схема примет вид, показанный на рис. 5.
). Тогда структурная схема примет вид, показанный на рис. 5.
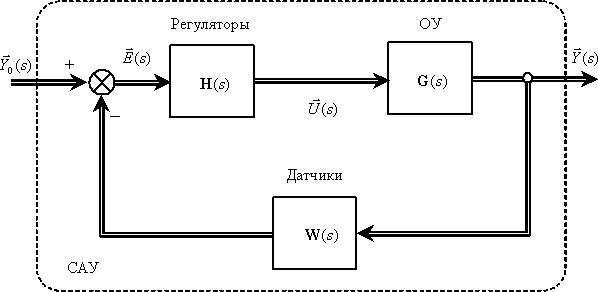
Рис. 5
Определим 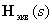 , удовлетворяющую следующему матричному операторному уравнению –
, удовлетворяющую следующему матричному операторному уравнению –
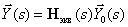 .
.
Для определения 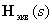 воспользуемся преобразованием матричных операторных уравнений, которые могут быть записаны по матричной структурной схеме.
воспользуемся преобразованием матричных операторных уравнений, которые могут быть записаны по матричной структурной схеме.
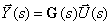
| (3) |

| (4) |
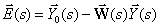
| (5) |
Подставим  из (4) в (3)
из (4) в (3)
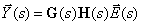
| (6) |
Подставим 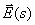 из (5) в (6)
из (5) в (6)
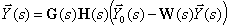
| (7) |
Раскроем скобки в правой части (7)

| (8) |
Перенесем слагаемое с 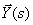 из правой части выражения (8) в левую часть
из правой части выражения (8) в левую часть
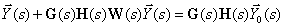
| (9) |
Вынесем 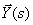 за скобку вправо
за скобку вправо
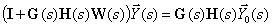
| (10) |
где 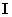 - единичная матрица
- единичная матрица 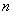 -го порядка.
-го порядка.
Если
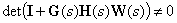 ,
,
тогда матрица
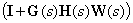 ,
,
является невырожденной и от нее может быть получена обратная матрица –
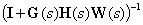
| (11) |
Умножим левую и правую части уравнения (10) справа на обратную матрицу (11), после несложных преобразований получаем –

Тогда получаем окончательно –
 .
.
Следовательно

| (12) |
По выражению (12), зная выражения матриц элементов системы, всегда можно определить передаточную матрицу системы в целом.
Контрольные вопросы и задачи
1. Дайте определение матричной структурной схеме.
2. В каких формах могут быть представлены матричные структурные схемы?
3. Определите вектор  , если вектор
, если вектор  имеет вид –
имеет вид –
 ,
,
векторы связаны уравнением –
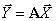 ,
,
где
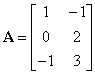 ,
,
Ответ:
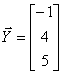 .
.
4. По матричному уравнению
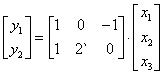 ,
,
определите 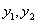 .
.
Ответ:
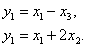
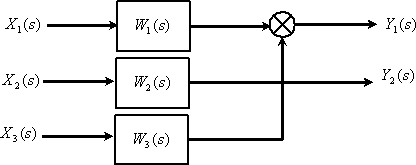
5. Объект управления описывается передаточной матрицей –
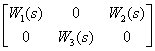 ,
,
которая связывает векторы –

Изобразить структурную схему, связывающую компоненты векторов 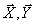 .
.
Ответ:
6. Дайте определение передаточной (эквивалентной) матрицы.
7. Дайте определение компонентам передаточной матрицы объекта управления.
8. Какими способами могут быть определены передаточные матрицы многомерных объектов.
9. Для многомерной системы, показанной на рис. 1, определите передаточную матрицу, связывающую векторы 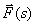 и
и 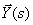 .
.
Ответ:
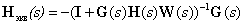 .
.
Лекция 14 Математические модели в пространстве состояний
Основу математической модели многомерной системы во временной области составляет векторно-матричная форма записи системы дифференциальных уравнений первого порядка, которая носит название уравнения состояния. Уравнение состояния имеет вид –

| (1) |
где 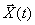 — вектор состояния размерности
— вектор состояния размерности 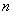 , который включает в себя переменные объекта, однозначно определяющие его состояние,
, который включает в себя переменные объекта, однозначно определяющие его состояние,

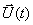 — вектор управления или входа размерности
— вектор управления или входа размерности 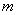 , который включает в себя сигналы, действующие на систему извне,
, который включает в себя сигналы, действующие на систему извне,
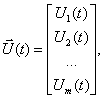
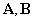 — матрицы параметров, включающие в себя параметры системы, размерность которых соответственно
— матрицы параметров, включающие в себя параметры системы, размерность которых соответственно 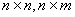 ,
,

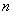 — порядок системы.
— порядок системы.
Иногда уравнение состояния (1) записывают в развернутой форме –
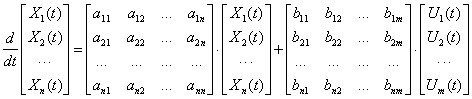 .
.
Уравнение состояния и структура полностью описывают объект управления, вектор состояния содержит переменные объекта, которые однозначно описывают его состояние.
Но в реальных системах многие компоненты не могут быть измерены или наблюдаемы с помощью датчиков. Эту ситуацию разрешает введение дополнительного уравнения выхода, которое определяет те переменные, которые доступны для наблюдения (на выходе системы) –
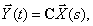
| (2) |
где 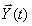 — вектор выхода размерности
— вектор выхода размерности 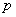 , который содержит переменные объекта, доступные для наблюдения,
, который содержит переменные объекта, доступные для наблюдения,
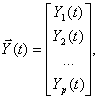
 — матрица параметров размерности
— матрица параметров размерности 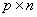 –
–

в системах управления 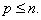
Уравнение выхода (2) также можно записать в развернутой форме

Графически уравнение состояния и уравнение выхода могут быть представлены в виде, показанном на рис. 1.
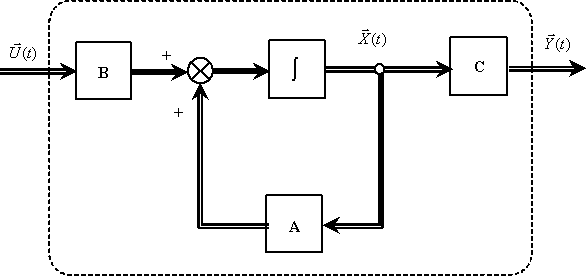
Рис. 1
Символ интегрирования на схеме означает покомпонентное интегрирование векторной величины.
В общем виде пространство состояний 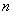 — мерной системы задается радиус-вектором
— мерной системы задается радиус-вектором 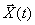 в координатной системе, оси которой определяются компонентами вектора состояния, как это показано на рис. 2.
в координатной системе, оси которой определяются компонентами вектора состояния, как это показано на рис. 2.
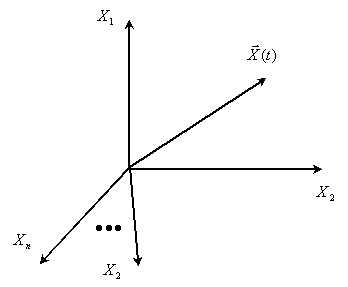
Рис. 2
Рассмотрим несколько примеров представления процессов в пространстве состояний.
Пример
Рассмотрим в пространстве состояний процесс пуска электродвигателя (М) постоянного тока с постоянными магнитами, принципиальная схема установки показана на рис. 3. Пуск производится подключением с помощью контакта (К) напряжения  , при этом в цепи будет протекать ток
, при этом в цепи будет протекать ток  и двигатель будет вращать вал с нагрузкой (Н) со скоростью
и двигатель будет вращать вал с нагрузкой (Н) со скоростью  , ток и скорость определяются с помощью датчиков соответственно ДТ ДС.
, ток и скорость определяются с помощью датчиков соответственно ДТ ДС.
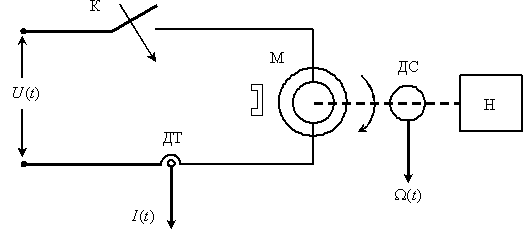
Рис. 3
Состояние двигателя в данном случае однозначно определяется током и скоростью двигателя, поэтому вектор состояния задаем в следующем виде –
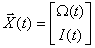 .
.
Вектор входа будет иметь только одну компоненту  . Графики изменения во времени переменных двигателя показаны на рис. 4.
. Графики изменения во времени переменных двигателя показаны на рис. 4.

Рис. 4
На рис. 4 введены обозначения: 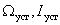 — установившиеся значения соответственно скорости и тока,
— установившиеся значения соответственно скорости и тока, 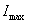 – максимальное значение тока при пуске.
– максимальное значение тока при пуске.
Сформируем двухмерное пространство состояний двигателя с траекторией движения конца вектора состояния в процессе пуска, для этого откладываем проекции вектора, то есть ток и скорость, в одинаковые моменты времени.
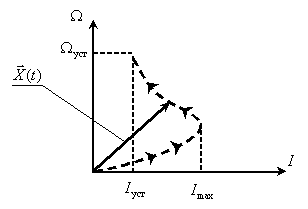
Рис. 5
Пример
Рассмотрим в пространстве состояний процесс позиционирования, то есть перемещения вала в заданное положение  , в автоматизированном электроприводе, показанном на рис. 6.
, в автоматизированном электроприводе, показанном на рис. 6.

Рис. 6
В этом случае состояние двигателя и всей системы электропривода в целом определяют три переменные двигателя ток  , скорость
, скорость  и положение вала
и положение вала 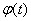 –
–
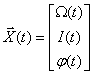 .
.
Графики изменения во времени переменных двигателя показаны на рис. 7.

Рис. 7
Сформируем трехмерное пространство состояний электропривода с траекторией движения конца вектора состояния в процессе позиционирования по временным графикам изменения компонент вектора состояния.
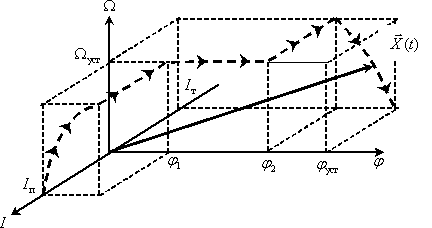
Рис. 8
Теперь рассмотрим получения математической модели многомерного объекта в виде уравнений состояния на примере двухмассовой упругой механической системы, показанной на рис. 9.
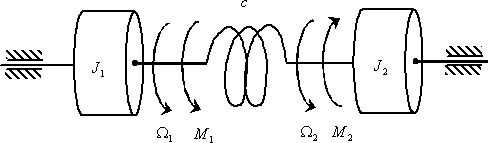
Рис. 9
Двухмассовая упругая система представляет собой механическую систему, состоящую из двух вращающихся масс с моментами инерции 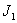 и
и 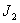 . К каждой массе прикладывается извне момент (
. К каждой массе прикладывается извне момент (  и
и 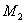 ), массы соединены валом, обладающим упругими свойствами (
), массы соединены валом, обладающим упругими свойствами ( 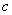 ), массы вращаются со скоростями
), массы вращаются со скоростями 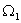 и
и 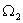 .
.
Система дифференциальных уравнений, описывающих систему, имеет вид –

| (3) |
где 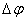 – разность углов положения первой
– разность углов положения первой 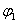 и второй
и второй 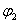 масс.
масс.
Так как уравнения состояния (1) и выхода (2) имеют единый для всех линейных систем вид, поэтому, чтобы определить их для конкретной системы мы должны выполнить следующее:
· задать векторы состояния и входа, определив тем самым порядок системы и порядок вектора входа,
· определить матрицы параметров уравнений.
Состояние системы определяется тремя переменными 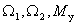 , поэтому задаем вектор состояния следующего вида –
, поэтому задаем вектор состояния следующего вида –
 .
.
Порядок системы 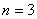 . Заметим, что положение переменных в векторе состояния можно задать произвольно, но в дальнейшем изменять его нельзя. Вектор входа определяется сигналами, действующими на систему извне, а это – моменты
. Заметим, что положение переменных в векторе состояния можно задать произвольно, но в дальнейшем изменять его нельзя. Вектор входа определяется сигналами, действующими на систему извне, а это – моменты  и
и 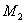 , поэтому вектор входа имеет вид –
, поэтому вектор входа имеет вид –
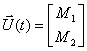 .
.
Порядок вектора выхода 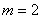 . Здесь также порядок следования компонент может быть произвольным, но фиксированным в дальнейших операциях.
. Здесь также порядок следования компонент может быть произвольным, но фиксированным в дальнейших операциях.
Преобразуем уравнения системы (3) к форме Коши –

| (4) |
Нам требуется получить уравнение состояния для системы третьего порядка с вектором входа второго порядка, посмотрим, что представляет собой это уравнение в общем виде –
 .
.
Раскрывая матричные скобки, получим –
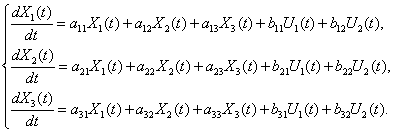
| (5) |
Теперь можно сформулировать задачу следующего этапа. Необходимо привести систему (4) в виду (5), для этого следует:
· расположить уравнения в порядке следования компонент в векторе состояния,
· расположить слагаемые в правых частях слева на право в порядке следования сначала компонент вектора состояния, затем вектора входа,
· отсутствующие слагаемые заменяем произведениями переменных на нулевые коэффициенты.
В результате коэффициенты в правых частях при соответствующих компонентах векторов состояния и входа будут компонентами искомых матриц уравнения состояния.
Преобразуем систему (4) к виду (5), в результате получим –
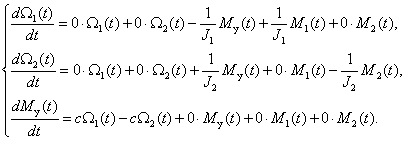
| (6) |
В результате по коэффициентам слагаемых в правых частях (6) получим искомые матрицы параметров уравнения состояния –
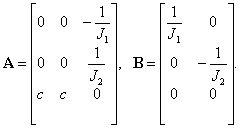
Уравнение состояния в развернутом виде –

Вид уравнения выхода определяется тем, какие компоненты вектора состояния доступны для наблюдения. В электромеханических системах электроприводов, эквивалентом которых является упругая двухмассовая система, возможны три варианты датчиковых систем (полагаем датчики безынерционными, а коэффициенты преобразования датчиков единичными):
1. Датчики скорости установлены на обеих массах. Тогда имеем следующее уравнение выхода –
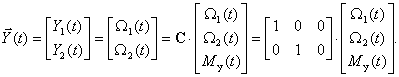
То есть имеем 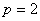 ,
,

2. Датчик скорости установлен на первой массе, уравнение выхода –

 ,
, 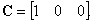
3. Датчик скорости установлен на второй массе, уравнение выхода –
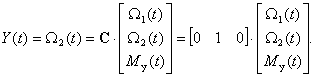
 ,
, 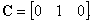
Контрольные вопросы и задачи
1. Перечислите компоненты уравнения состояния (векторы и матрицы), их размерности.
2. Поясните смысл уравнения выхода, перечислите компоненты и их размерности.
3. По системе дифференциальных уравнений, описывающих многомерную систему –
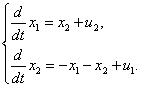 ,
,
полагая векторы состояния и входа –
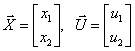 ,
,
записать уравнение состояния в развернутой форме.
Ответ:
 .
.
4. По уравнению состояния
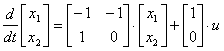 ,
,
описывающему многомерную систему, определить систему дифференциальных уравнений, связывающих компоненты векторов состояния и входа.
Ответ:
. 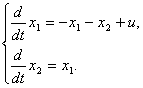 .
.
5. По системе дифференциальных уравнений, описывающих многомерную систему –
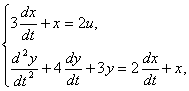
полагая векторы состояния и входа –
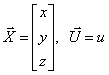 ,
,
записать уравнение состояния в развернутой форме.
Ответ:
 .
.
Лекция 13 Методы оценки качества систем управления
К процессам систем автоматического управления предъявляются три основные группы требований:
1. Требования по точности в установившихся режимах.
2. Требования к устойчивости.
3. Требования к качеству переходных процессов.
Кроме этих к системам на практике так же предъявляются требования технико-экономического характера, связанные со спецификой объекта управления или технологического процесса.
В нашем курсе мы будем рассматривать только требования к качеству переходных процессов, динамики систем, как вопрос не только тесно связанный с математическим моделированием систем, но и связанный с использованием разнообразного математического аппарата. Требования по точности в установившихся режимах и требования к устойчивости будут рассмотрены в дисциплинах "Теория автоматического управления", "Системы управления электроприводами", "Автоматизация типовых производственных процессов и промышленных установок".
В промышленных установках с системами автоматического управления можно выделить две большие группы:
1. Установки, в которых время переходного процесса пренебрежимо мало по сравнению с установившимся режимом. В этих случаях динамические режимы не оказывают существенного влияния ни на качество продукции, ни на производительность оборудования, на пример, насосы, вентиляторы, транспортеры и т. д.
2. Установки, в которых время переходного процесса соизмеримо с временем установившихся режимов, или, такие, в которых отклонение регулируемой переменной в динамике существенно влияет на качество продукции, на пример, станки, роботы, следящие системы и т. д.
Устойчивость, то есть способность к затуханию переходных процессов, является необходимым, но далеко не достаточным условием практической пригодности систем. Этот критерий позволяет очень грубо оценить переходные процессы. Рассмотрим, как выглядят переходные характеристики для трех основных режимов с точки зрения устойчивости.

Рис. 1
Использовав, как показано на рис. 1, критерий устойчивости по виду переходной характеристики (переходного процесса), мы можем сказать, что система устойчива, если переходный процесс затухает. Однако система может быть устойчивой, но ее переходные процессы, в зависимости от изменения параметров, будут сильно различаться, как это показано на рис. 2.
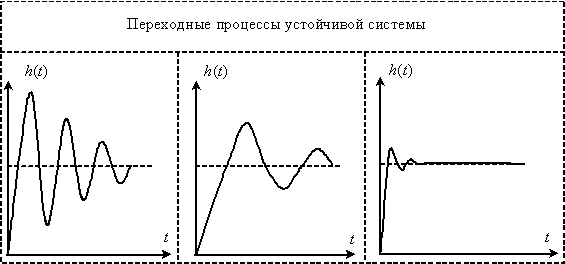
Рис. 2
Мы видим, что эти процессы существенно отличаются по виду, имеют разные частоту колебаний, время завершения, амплитуду отклонения от заданной величины. В связи с этим возникает необходимость сравнения, оценки устойчивых временных характеристик систем.
Следует отметить, что специалистов интересует не только переходные процессы при изменении управляющих воздействий, но и переходные процессы при изменении возмущающих воздействий.
Таким образом, важным понятие для систем управления является понятие качества переходных процессов, то есть становится важным сам характер протекания процессов, особенно такие факторы, как длительность, колебательность и динамическое отклонение регулируемой переменной от заданной величины.
Для оценки качества переходных процессов требуются характеристики, критерии или показатели качества, которые могут быть выражены численно.
Критерии качества имеют следующие области применения:
1. Сравнительный анализ систем автоматического управления при изменении параметров объекта управления, или при сравнении систем разного вида для одного и того же объекта управления.
2. Синтез, выбор параметров систем автоматического управления, обеспечивающих заданные критерии качества переходных процессов, требованиям технического задания на разработку системы.
Известно, что переходный процесс в системе управления зависит не только от свойств самой системы, но и от характера (вида) входного воздействия. Поэтому поведение системы при оценке качества переходных процессов рассматривают при типовых внешних воздействиях. В качестве таких типовых воздействий чаще всего используют:
· единичную ступенчатую функцию, реже, линейнонарастающий сигнал,
· воздействие гармонической функцией.
Оценки качества делятся на две группы:
1. Прямые показатели качества переходных процессов. Они характеризуют непосредственно сам переходный процесс, реакцию системы на типовое воздействие, чаще всего, на единичную ступенчатую функцию.
2. Косвенные показатели (критерии) качества. Они оценивают качество переходных процессов по другим характеристикам системы, таким как частотные характеристики, характер и расположение корней характеристического уравнения (полюсов передаточной функции), интегралы временной функции переходного процесса.
Оценка качества переходного процесса при воздействии ступенчатой функции
Прямые оценки качества определяют по графику переходной характеристики системы управления 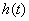 , то есть при воздействии на систему единичной ступенчатой функции –
, то есть при воздействии на систему единичной ступенчатой функции –
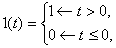
и при нулевых начальных условиях, или по кривой переходного процесса регулируемой переменной  при воздействии на вход ступенчатой функции с амплитудой, соответствующей номинальному или иному определенному значению регулируемой переменной.
при воздействии на вход ступенчатой функции с амплитудой, соответствующей номинальному или иному определенному значению регулируемой переменной.
· Рассмотрим систему управления с единичной отрицательной обратной связью, структурная схема которой показана на рис. 2.
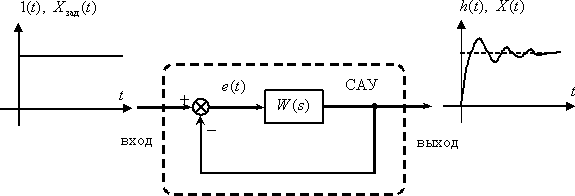
Рис. 3
На вход системы поступает ступенчатый сигнал, на выходе можно наблюдать реакцию системы, кроме того, в качестве переходного процесса может рассматриваться изменение ошибки регулирования –
 .
.
Примерные графики изменения сигнала на выходе и ошибки регулирования показаны соответственно на рис. 4 и 5.

Рис. 4
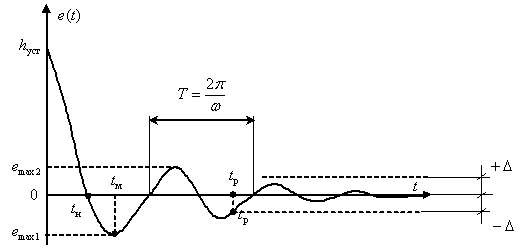
Рис. 5
Рассмотрим прямые оценки качества переходных процессов, показанные на рис. 4 и 5:
1. 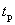 – минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью –
– минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью –
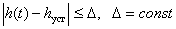 .
.
 предварительно задается в процентах от установившегося значения
предварительно задается в процентах от установившегося значения 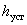 , где нет определенных требований – принимают
, где нет определенных требований – принимают 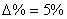 .
.
2. 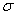 – перегулирование – максимальное отклонение от установившегося значения, выраженное в относительных единицах или процентах –
– перегулирование – максимальное отклонение от установившегося значения, выраженное в относительных единицах или процентах –
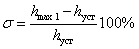 или
или 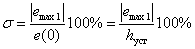 .
.
Обычно требования по перегулированию составляют 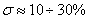 , иногда к качеству процессов может быть предъявлено требование
, иногда к качеству процессов может быть предъявлено требование  , на пример в системах позиционирования манипуляторов промышленных роботов.
, на пример в системах позиционирования манипуляторов промышленных роботов.
3. 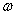 – частота колебаний –
– частота колебаний –
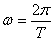 ,
,
где 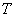 – период колебаний для колебательных процессов.
– период колебаний для колебательных процессов.
4.  – это число полных колебаний, которое имеет
– это число полных колебаний, которое имеет 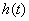 или
или 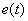 за время регулирования
за время регулирования 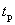 , обычные требования по числу колебаний
, обычные требования по числу колебаний 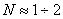 , в некоторых системах накладывают ограничение на колебательность
, в некоторых системах накладывают ограничение на колебательность 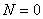 , на пример, в системах с существенным люфтом в механических передачах.
, на пример, в системах с существенным люфтом в механических передачах.
5.  – время достижения первого максимума.
– время достижения первого максимума.
6. 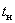 – время нарастания переходного процесса, время от начала переходного процесса до момента первого пересечения графиком линии установившегося значения.
– время нарастания переходного процесса, время от начала переходного процесса до момента первого пересечения графиком линии установившегося значения.
7. 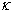 – декремент затухания, равный отношению модулей двух смежных перегулирований –
– декремент затухания, равный отношению модулей двух смежных перегулирований –
 .
.
Перечисленные выше показатели могут быть дополнены и другими, если этого требуют специфические технические задания на разработку или исследование систем управления.
Устойчивые переходные процессы, возникающие при ступенчатом воздействии, принято делить на три группы:
1. Монотонные процессы. Такие процессы, где первая производная выходной величины по времени не меняет знак.
2. Апериодические процессы. Здесь производная меняет знак не более одного раза.
3. Колебательные процессы. Производная меняет свой знак периодически
На рис. 6 показан примерный вид колебательного, апериодического и монотонного процессов.

Рис. 6
Требования к качеству переходного процесса могут быть представлены графически. Они сводятся к требованию, чтобы отклонение регулируемой величины при ступенчатом воздействии не выходило за границы некоторой области, изображенной на диаграмме качества процесса. Простейшая диаграмма показана на рис. 7.

Рис. 7
Уточненная диаграмма, в которой накладываются ограничения на скорость нарастания сигнала, показана на рис. 8. На уточненной диаграмме  обозначает время запаздывания, равное отрезку времени, заключенному между моментами приложения скачкообразного сигнала (
обозначает время запаздывания, равное отрезку времени, заключенному между моментами приложения скачкообразного сигнала ( 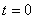 ) и моментом времени, при котором выходная величина достигает половины установившегося значения.
) и моментом времени, при котором выходная величина достигает половины установившегося значения.

Рис. 8
Контрольные вопросы и задачи
1. В каких системах автоматического управления важен характер и параметры протекания переходных процессов?
2. Перечислите основные области применения критериев качества.
3. Какие показатели качества относят к прямым показателям?
4. Какие показатели (критерии) качества относят к косвенным критериям?
5. Как определить время регулирования по графику переходного процесса?
6. Как определить перегулирование по графику переходного процесса?
7. Как определить время нарастания по графику переходного процесса?
8. Какие переходные процессы относят к апериодическим процессам?
9. Какие переходные процессы относят к монотонным процессам?
Лекция 14 Оценка качества при гармонических воздействиях
Качество переходных процессов в системах и объектах при гармонических воздействиях оценивают по частотным характеристикам, снятым экспериментально или рассчитанным по параметрам математической модели. В этом случае получают частотные критерии качества переходных процессов, которые относят к косвенным критериям.
Частотные критерии определяют по одной из частотных характеристик: амплитудно-фазовой, амплитудной, вещественной или логарифмической амплитудной. Рассмотрим в качестве основы определение косвенных показателей качества по амплитудной частотной характеристике (АЧХ) систем.
1.  – показатель колебательности, определяемый как отношение максимального значения АЧХ к ее значению при
– показатель колебательности, определяемый как отношение максимального значения АЧХ к ее значению при 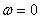
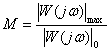
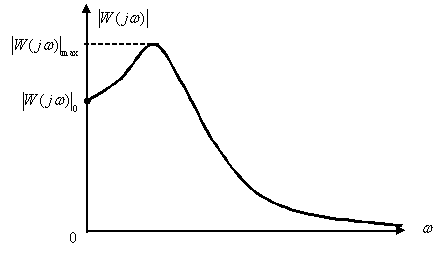
Рис. 1
Показатель колебательности характеризует склонность систем или объектов к колебательности. Чем выше показатель колебательности, тем более колебательна система, то есть менее качественна.
При 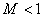 переходная характеристика системы неколебательная, а АЧХ системы имеет примерный вид, показанный на рис. 2.
переходная характеристика системы неколебательная, а АЧХ системы имеет примерный вид, показанный на рис. 2.
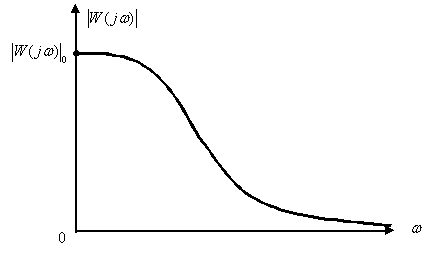
Рис. 2
Если 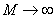 , то говорят о незатухающих колебаниях переходной характеристики, а АЧХ системы имеет вид, показанный на рис. 3.
, то говорят о незатухающих колебаниях переходной характеристики, а АЧХ системы имеет вид, показанный на рис. 3.
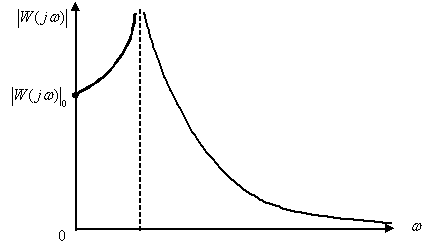
Рис. 3
Считается допустимым, если 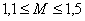 .
.
2. 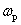 – резонансная частота системы или объекта, при которой АЧХ имеет максимум.
– резонансная частота системы или объекта, при которой АЧХ имеет максимум.

При  гармонические сигналы проходят через систему с наибольшим усилением.
гармонические сигналы проходят через систему с наибольшим усилением.
3. Полоса пропускания системы управления – это интервал частот от  до частоты
до частоты  , в котором выполняется условие
, в котором выполняется условие
 .
.
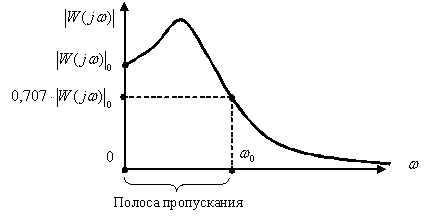
Рис. 4
Полоса пропускания систем не должна быть очень широкой, чтобы не проходили высокочастотные помехи. С другой стороны, чем выше частота сигналов, которые пропускает система, тем выше ее быстродействие. В электроприводах полосу пропускания задают в герцах, для систем управления скоростью вращения двигателя полоса пропускания, в зависимости от типа двигателя и преобразователя энергии, находится в диапазоне  Гц,
Гц,
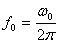 ,
,
при этом накладывается дополнительное ограничение о том, что фазочастотная характеристика в полосе пропускания не должна опускаться ниже 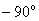 .
.
4. 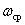 – частота среза, при которой АЧХ системы принимает значение, равное единице
– частота среза, при которой АЧХ системы принимает значение, равное единице
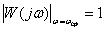 ,
,
как это показано на рис. 5.

Рис. 5
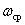 косвенно характеризует длительность переходного процесса, так же как и
косвенно характеризует длительность переходного процесса, так же как и  . Время регулирования системы обратно пропорционально частоте среза –
. Время регулирования системы обратно пропорционально частоте среза –
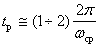 ,
,
если переходный процесс имеет 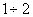 колебания, то можно установить связь между частотой среза т временем достижения первого максимума –
колебания, то можно установить связь между частотой среза т временем достижения первого максимума –
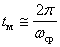 .
.
Полоса среза, как характеристика быстродействия систем получила распространение, так как она легко определяется на логарифмических частотных характеристиках (см. рис. 6).
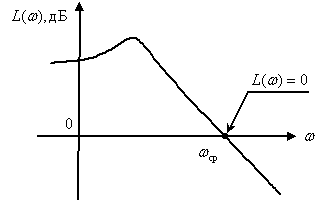
Рис. 6
Интегральные оценки качества
Интегральными оценками качества переходного процесса систем управления называют интегралы по времени от некоторых функций переходного процесса изменения ошибки регулирования.
Рассмотрим скалярную линейную систему, показанную на рис. 7. На вход управления системы поступает ступенчатый сигнал с амплитудой 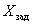 , система предназначена для стабилизации заданного значения регулируемой переменной
, система предназначена для стабилизации заданного значения регулируемой переменной  , на систему так же может действовать скалярное ступенчатое возмущение
, на систему так же может действовать скалярное ступенчатое возмущение  стремящееся снизить значение регулируемой переменной.
стремящееся снизить значение регулируемой переменной.
Рис. 7
Примерный вид графиков переходных процессов регулируемой величины  и ошибки регулирования –
и ошибки регулирования –
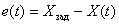 ,
,
показаны соответственно на рис. 8 и 9.

Рис. 8
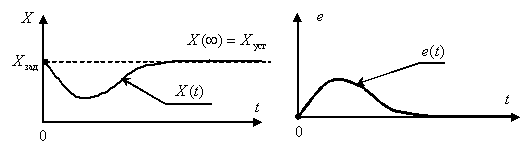
Рис. 9
Основные области применения интегральных оценок в теории автоматического управления:
1. Общая оценка быстроты затухания и величины отклонения регулируемой величины в совокупности, без определения того и другого в отдельности.
2. Выбор при синтезе параметров систем, обеспечивающих оптимальность переходного процесса с точки зрения достижения минимума интегральных оценок.
Простейшей интегральной оценкой может служить линейная интегральная оценка следующего вида –
 .
.
Геометрическая интерпретация этого интеграла представляет собой площадь под кривой 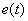 , как это показано на рис. 10 для переходных процессов изменения ошибки при управлении и возмущении.
, как это показано на рис. 10 для переходных процессов изменения ошибки при управлении и возмущении.
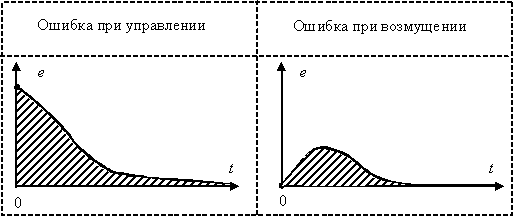
Рис. 10
Если система управления устойчива и обладает свойством астатизма, тогда
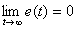 ,
,
а интеграл  стремится к конечному значению, равному площади под кривой
стремится к конечному значению, равному площади под кривой 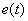 . Параметры системы управления стремятся выбирать таким образом, чтобы добиться минимума
. Параметры системы управления стремятся выбирать таким образом, чтобы добиться минимума  , при этом идеальный переходный процесс будет стремиться к идеальной ступенчатой форма.
, при этом идеальный переходный процесс будет стремиться к идеальной ступенчатой форма.
Контрольные вопросы и задачи
1. Как определить показатель колебательности по АЧХ системы?
2. Как определить частоту среза и полосу пропускания по АЧХ?
3. Как соотносятся частота среза системы и ее быстродействие?
4. Дайте определение линейной интегральной оценке, укажаите ее достоинства и недостатки.
5. Почему для интегральных оценок переходного процесса используют график изменения ошибки регулирования?
6. По графику АЧХ системы
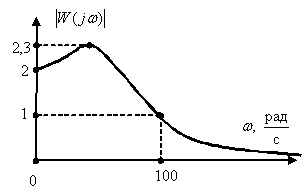
определить показатель колебательности и частоту среза системы.
Ответ:
Показатель колебательности 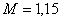 , частота среза
, частота среза  .
.
1. По графикам АЧХ двух систем: САУ1 – 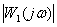 , САУ2 –
, САУ2 – 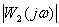 ,
,
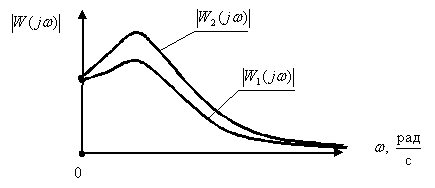
определить систему управления, переходные процессы которой имеют большую колебательность.
Ответ:
Большую колебательность переходных процессов имеет система САУ2.
1. По графикам АЧХ двух систем: САУ1 – 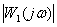 , САУ2 –
, САУ2 – 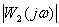 ,
,

определить систему управления, которая имеет большее быстродействие.
Ответ:
Большую колебательность переходных процессов имеет система САУ1.
Лекция 15 Корневые критерии качества переходных процессов
Эта группа критериев основана на оценке качества переходных процессов по значениям полюсов и нулей передаточной функции системы между интересующими нас входами и выходами системы.
Как известна, переходная характеристика системы может быть определена следующим образом –
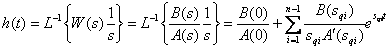
| (1) |
где 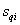 – корни характеристического уравнения системы
– корни характеристического уравнения системы
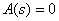 .
.
Очевидно, что на характер переходного процесса оказывает влияние и числитель 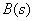 и знаменатель
и знаменатель 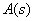 передаточной функции. Но, в большинстве случаев, при анализе систем по реакции на управляющее воздействие,
передаточной функции. Но, в большинстве случаев, при анализе систем по реакции на управляющее воздействие, 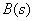 не имеет корней, то есть передаточная функция не имеет нулей. Тогда характер переходного процесса можно оценить только по полюсам передаточной функции, подвергая тем самым анализу корни характеристического уравнения системы –
не имеет корней, то есть передаточная функция не имеет нулей. Тогда характер переходного процесса можно оценить только по полюсам передаточной функции, подвергая тем самым анализу корни характеристического уравнения системы –

| (2) |
В случае приближенной оценки качества по корням характеристического уравнения на комплексной плоскости выделяют область расположения корней, границы которой задаются по требованиям к качеству процессов, как это показано на рис. 1.
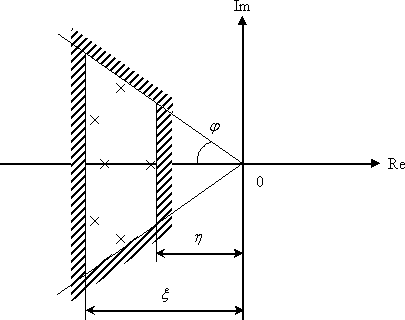
Рис. 1
Границы области, показанной на рис. 1, задаются следующими параметрами:
·  – критерий длительности переходного процесса,
– критерий длительности переходного процесса,
· 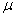 – колебательность переходного процесса, определяется по
– колебательность переходного процесса, определяется по 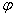 ,
,
· 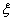 – максимальное удаление корня от мнимой оси.
– максимальное удаление корня от мнимой оси.
Рассмотрим эти параметры.
Критерий длительности  определяется как расстояние от мнимой оси до ближайшего действительного корня или ближайшей пары комплексно сопряженных корней.
определяется как расстояние от мнимой оси до ближайшего действительного корня или ближайшей пары комплексно сопряженных корней.
Выясним, действительно ли этот параметр характеризует длительность переходного процесса? Возможны два случая расположения корней на границе области.
1. Пусть ближайшим к мнимой оси, то есть лежащий на границе области, будет действительный корень –
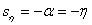 ,
,
тогда соответствующая ему компонента переходного процесса, в соответствии с (1) будет иметь вид –
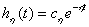
| (3) |
где 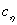 - коэффициент разложения (1).
- коэффициент разложения (1).
2. Если ближайшей к мнимой оси будет комплексно-сопряженная пара корней –
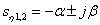 ,
,
тогда соответствующая им компонента переходного процесса, в соответствии с (1) будет иметь вид –
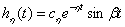
| (4) |
где 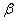 - частота колебаний.
- частота колебаний.
Из (3) и (4) мы видим, что время затухание компоненты 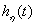 определяет сомножитель –
определяет сомножитель –
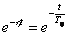 ,
,
где  – величина минимального действительного корня или минимальной действительной части корней,
– величина минимального действительного корня или минимальной действительной части корней, 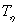 – соответствующая
– соответствующая  , наибольшая постоянная времени. Таким образом, можно считать, что переходный процесс системы завершится не раньше, чем затухнет компонента
, наибольшая постоянная времени. Таким образом, можно считать, что переходный процесс системы завершится не раньше, чем затухнет компонента 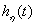 . Следовательно,
. Следовательно,  определяет длительность переходного процесса, будучи величиной, обратно пропорциональной времени регулирования. Зная
определяет длительность переходного процесса, будучи величиной, обратно пропорциональной времени регулирования. Зная  , мы можем оценить время регулирования или переходного процесса по следующему соотношению –
, мы можем оценить время регулирования или переходного процесса по следующему соотношению –
 ,
,
где  – половина ширины области, при попадании в которую переходной процесс считается завершенным. Если
– половина ширины области, при попадании в которую переходной процесс считается завершенным. Если 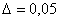 , а крайний корень действительный, то имеем –
, а крайний корень действительный, то имеем –
 .
.
Критерий колебательности 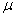 определяется по углу
определяется по углу 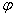 следующим образом –
следующим образом –
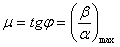 .
.
где 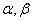 – соответственно действительная и мнимая части комплексно сопряженной пары корней расположенных на границе области (см. рис. 1). При увеличении
– соответственно действительная и мнимая части комплексно сопряженной пары корней расположенных на границе области (см. рис. 1). При увеличении 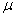 возрастает колебательность системы.
возрастает колебательность системы.
Дальнюю от мнимой оси границу области 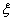 , определяют корни, оказывающие предельно малое влияние на переходный процесс.
, определяют корни, оказывающие предельно малое влияние на переходный процесс.
При прочих равных условиях от системы требую увеличения  и снижения
и снижения 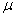 .
.
В качестве примера влияния расположения корней на характер переходных процессов покажем графики, представленные на рис. 2 и 3.
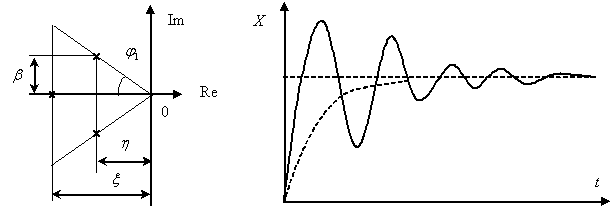
Рис. 2
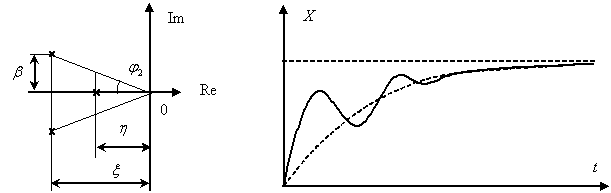
Рис. 3
Если передаточная функция системы имеет нули, то оценка качества системы только по полюсам может дать существенную погрешность.
Чтобы пояснить характер влияния нулей на качество переходных процессов, представим систему следующим образом, как это показано на рис. 4.
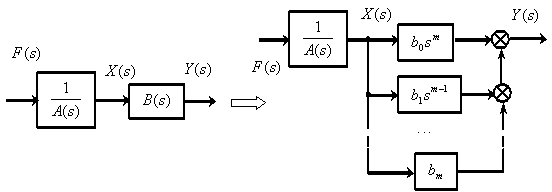
Рис. 4
Конкретизируем задачу, пусть
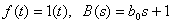 ,
,
а  имеет вид, показанный на рис. 5. При этом рассмотрим два варианта графика:
имеет вид, показанный на рис. 5. При этом рассмотрим два варианта графика: 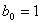 ,
, 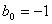 .
.
Из рассмотрения рис. 5 можно сделать вывод, что члены 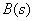 с положительными коэффициентами приводят к повышению колебательности и быстродействия, а отрицательные коэффициенты затягивают переходный процесс.
с положительными коэффициентами приводят к повышению колебательности и быстродействия, а отрицательные коэффициенты затягивают переходный процесс.
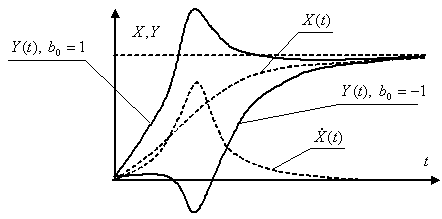
Рис. 5
Контрольные вопросы и задачи
1. Как объяснить влияние на переходные процессы корней характеристического уравнения?
2. Какую компоненту переходного процесса дает отрицательный действительный корень характеристического уравнения?
3. Какие компоненты переходного процесса дают комплексно сопряженные корни характеристического уравнения?
4. Что определяют корни характеристического уравнения ближе всего расположенные к мнимой оси комплексной плоскости?
5. Как связана с быстродействием системы величина среднегеометрического корня характеристического уравнения?
6. Какое влияние оказывает на переходный процесс нули передаточной функции?
7. В каких случаях следует использовать на настройки системы биномиальное распределение корней характеристического уравнения?
8. В каких случаях следует использовать на настройки системы распределение корней характеристического уравнения Баттерворта?
9. Определите коэффициенты характеристического уравнения с биномиальным распределением корней для системы управления третьего порядка, если требуемое время регулирования 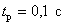 .
.
Ответ:
Желаемое характеристическое уравнение имеет вид –
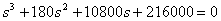 .
.
10. Определите коэффициенты характеристического уравнения с распределением корней по Баттерворту для системы управления четвертого порядка, если требуемое время регулирования 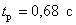 .
.
Ответ:
Желаемое характеристическое уравнение имеет вид –
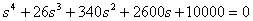 .
.
Рекомендуемая учебно-методическая литература по дисциплине:
1. Лебедев С. К. Конспект лекций «Математические основы теории автоматического управления». – Иваново: ИГЭИ, 150 с.
2. Теория автоматического управления/ Под ред. А. А. Воронова - М.: Высшая школа, 1986, ч. 1, 2.
3. Математические основы теории автоматического регулирования/ Под ред. Б. К. Чемоданова. - М.: Высшая школа, 1972, т. 1, 2.
4. Справочник по математике для научных работников и инженеров. Корн Г., Корн Т. - М.: Наука, 1984.
5. Теория систем автоматического регулирования. - Бессекерский В.А., Попов Е.П. М.: Наука, 1975.
6. Справочное пособие по теории автоматического регулирования и управления/ Под ред. П. А. Санковского. - Мн.: Высшая школа, 1973.
7. Трахтенберг Р. М. Теория автоматического управления. Нелинейные, импульсные, оптимальные, инвариантные, адаптивные и многомерные САУ. - Иваново: ИвГУ, 1990.
Дата добавления: 2018-04-05; просмотров: 1257; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
