Лекция 9. Динамика твердого тела
Лекция 1. Основные понятия и аксиомы механики Ньютона. Механика есть наука о механических движениях и взаимодействиях материальных тел. В курсе «Теоретическая механика» изучаются классические математические модели реальных тел: материальная точка, система материальных точек, абсолютно твердое тело. Основные понятия механики. Пространство, время, система отсчета, система координат. Масса. Пространство, в котором находятся материальные тела, моделируется как трехмерное и эвклидово, а время как одномерное. Масса тела, как мера его инертности, постоянна. Положение точки. В выбранной декартовой системе координат положение точки определяется упорядоченной тройкой действительных чисел x, y, z , координат точки (вектором ). Движение точки есть последовательное во времени изменение ее положения по отношению к выбранной системе отсчета. В декартовых координатах движение задается дважды дифференцируемым отображением : , то есть , t (1.1) Скорость и ускорение точки: (1.2) Связи. Уравнения связей. Если тело при движении контактирует с другими телами, то его положение в пространстве не может быть произвольным. Ограничения (связи) на положение тела записывают в виде уравнений геометрических связей. Три координаты точки связаны уравнениями связей. Поэтому число независимых координат точки меньше трех. Число независимых координат точки (обобщенных координат) называют ее числом степеней свободы. Ограничения на скорость и ускорение точки представляют в виде кинематических уравнений связей, которые получают из геометрических уравнений их дифференцированием по времени. Пример 1. Математический маятник есть точка, подвешенная на нити, имеющей постоянную длину , которая движется в вертикальной плоскости z = 0 по части окружности. Уравнения геометрических связей: , z = 0. Три координаты связаны двумя уравнениями. Поэтому имеется одна независимая координата. Точка имеет одну степень свободы. Уравнения кинематических связей точки маятника: , . (1.3) Взаимодействие тел: силы действия и противодействия. .Механические взаимодействия тел вызывают движение этих тел или деформируют их. Сила – мера взаимодействия тел есть вектор. Силу действия называют активной силой, силу противодействия – силой реакции. Для некоторых взаимодействий тел свойства сил взаимодействий формулируют в аксиомах сил и их моментов. Механика Ньютона. Модель «материальная точка». Аксиомы (принципы) механики Ньютона – три закона Ньютона. 1. Первый закон Ньютона. Существуют системы отсчета (инерциальные системы), в которых изолированная материальная точка (равнодействующая всех сил ее взаимодействий с другими телами равна нулю), сохраняет покой или движется равномерно и прямолинейно. 2. Второй закон Ньютона (в векторной форме и в декартовых координатах): , (1.4) . 3. Третий закон Ньютона. Для двух взаимодействующих тел сила действия равна по величине и противоположна по направлению силе противодействия. Векторы сил имеют общую линию действия. . (1.5) Уравнения (1.4) есть дифференциальные уравнения движения точки в декартовых координатах. Основные задачи динамики материальной точки. Прямая задача: нахождение сил по известному движению (или его характеристикам). Пример прямой задачи. Снаряд массой m вылетает из ствола орудия на поверхности Земли со скоростью v0 под углом α к горизонту. Движение снаряда в декартовых координатах известно: Здесь есть постоянное ускорение свободного падения точки у Земли. Какая сила вызвала это движение? Обратная задача. Нахождение движения по известным силам взаимодействий известному начальному состоянию. Пример обратной задачи. Снаряд, моделируемый как материальная точка, притягивается к Земле с постоянной силой притяжения к Земле (силой тяжести ). Найти движение снаряда, если в начальный момент времени его выпустили с Земли со скоростью v0 под углом α к горизонту. В этом случае движение точки есть решение дифференциальных уравнений (1.4), которое однозначно определяется начальным состоянием точки – начальным положением и начальной скоростью точки. Задача 1.1. Найти траекторию снаряда, дальность L его полета до Земли, максимальную высоту H подъема снаряда, а также время T его полного полета. Задача 1.2. В условиях предыдущей задачи, найти время полета снаряда, если он упал в яму глубиной h. Задача 1.3. Найти силу реакции T нити математического маятника в нижнем положении точки на окружности , если в этом положении скорость точки равна . Ось 0y направлена по вертикали вниз. Решение. Уравнения связей (1.3) справедливы для любого положения точки на окружности. В нижнем положении точки оно принимает вид: . Из второго уравнения закона Ньютона (1.4) получаем: , откуда, используя предыдущее уравнение, получаем значение силы реакции в нижнем положении маятника: . Задача 1.4. Капсула спускаемого аппарата с космонавтом на большой высоте H над Землей имела скорость vН . Какова скорость vЗ снаряда у поверхности Земли, если пренебречь вращением капсулы и сопротивлением воздуха. Учесть гравитационную силу притяжения снаряда к Земле, обратно пропорциональную квадрату расстояния от снаряда до центра «неподвижной» Земли. Радиус Земли равен R . На поверхности Земли сила притяжения равна mg . Решение. Выберем ось 0x от центра 0 Земли вдоль прямолинейной траектории движения космонавта (как точки). Проекция на ось 0x силы притяжения , с учетом ее значения на Земле , равна . Второй закон Ньютона в проекции на ось 0x имеет вид: . (1.6) В обратной задаче динамики требуется проинтегрировать уравнение движения с учетом начального состояния. За независимые параметры примем положение и скорость точки, тем более что начальные значения этих параметров заданы. Так как , то, разделяя в уравнении (1.6) переменные x, , получим: , (1.7) Для решения задачи достаточно проинтегрировать (1.7) один раз. Получаем: . Интегрирование этого уравнения дает следующее значение скорости космонавта при подлете к Земле: . Лекция 2. Движение вдоль траектории. Скорость и ускорение точки в проекциях на естественный ортонормированный базис. Траектория точки есть геометрическое место всех последовательных положений точки при ее движении. Пусть это есть некоторая гладкая кривая линия в . Пусть траектория известна и задана в параметрической форме: (2.1) В таком случае, в силу уравнений (3.1), как уравнений геометрических связей, точка имеет один независимый параметр t (одну степень свободы). Выберем, однако, вместо t другой независимый параметр - дуговую координату s - расстояние вдоль кривой от некоторого начального положения точки O на траектории до ее текущего положения. При движении точки по траектории и (2.2) Далее при записи уравнения траектории примем в качестве независимого параметра дуговую координату s: (2.3) Касательный к траектории вектор определим следующим образом: (2.4) Вектор главной нормали перпендикулярен к вектору и определяется следующим образом: (2.5) Величина называется кривизной кривой в точке М, а величина называется радиусом кривизны. В каждой точке траектории три единичных вектора и взаимно перпендикулярны и образуют естественный ортонормированный базис, ориентация векторов которого определяется видом траектории и положением точки М на траектории. Движение точки в естественной форме (2.6) Скорость точки направлена параллельно вектору : (2.7) а её проекция на ось равна: Ускорение точки раскладывается по естественному базису так: Компоненты вектора ускорения называются так: касательное , нормальное и бинормальное ускорения. Окончательно: (2.8) Закон Ньютона в проекциях на естественный базис запишем в виде: (2.9) Если траектория точки есть окружность с радиусом R , то кривизна окружности равна, по определению, радиусу окружности, и поэтому нормальное ускорение точки есть (2.10) Задача 2.1. Материальная точка массы m движется в поле силы тяжести по гладкой неподвижной окружности радиуса R в вертикальной плоскости. Написать дифференциальное уравнение движения точки. Дуговую координату s отсчитывать от её нижнего положения. Найти скорость точки в любом её положении, если в нижнем положении она равна v0 . При какой начальной скорости v0 0 точка пройдет всю окружность? Решение. Закон Ньютона в проекции на касательный вектор к траектории имеет вид: (2.11) Это есть дифференциальное уравнение движения математического маятника. Для того, чтобы найти движение, нужно интегрировать это уравнение. Однако его нельзя проинтегрировать в элементарных функциях. Решение в эллиптических функциях показывает, что движение точки периодическое, но период колебаний не есть постоянная величина. Для нахождения начальной скорости, при которой точка пройдет всю окружность, используем закон сохранения механической энергии, который можно получить интегрированием (3.11) один раз, и условие того, что в верхней точке траектории скорость больше нуля: Ответ: Задача 2.2. Материальная точка массы m движется по гладкой неподвижной кривой в виде ветви циклоиды в вертикальной плоскости в поле силы тяжести mg.Уравнение траектории в параметрической форме имеет вид: При движении точки по траектории Для любого положения точки М на циклоиде угол есть угол между касательной к кривой и горизонталью. Ось Оx горизонтальна, а Оy направлена вертикально вверх. Выбрав за начало отсчета дуговой координаты s низшее положение точки М на траектории, найти движение точки в естественной форме s = s(t). Найти также силу реакции кривой R для любого положения s точки на циклоиде, если в начале координат точка имеет минимальную скорость. Решение. Определим векторы естественного ортонормированного базиса и : Кривизна кривой и радиус кривизны имеют вид: Длина дуговой координаты s, отсчитываемой из низшего положения на траектории, равна: Закон Ньютона в естественном базисе (2.9) запишем в виде: откуда получаем движение точки в естественном виде: Это решение есть гармоническое колебание с постоянной круговой частотой колебаний и с постоянным периодом колебаний Тяжелую точку в её движении по циклоиде называют циклоидальным маятником. Сила реакции циклоиды находится из закона Ньютона (2.9) в проекции на нормаль к траектории: Скорость точки находится из закона сохранения механической энергии: Ответ: Лекция 3. Криволинейные системы координат. Декартовой системой координат в R3 называется совокупность точки О, начала координат, и трех векторов I =1, 2, 3. -- векторов ортонормированного базиса. Определение. Каждой точке с координатами = (x, y, z)T сопоставим три упорядоченных числа k1 , k2 , k3, по некоторому правилу: (3.1) Назовем ki , i = 1, 2 ,3, криволинейными координатами точки М. Функции (3.1) взаимно однозначны и непрерывно дифференцируемы по всем координатам и имеют обратные функции в некоторой области взаимной однозначности (3.2) Определение. Три вектора называются базисом криволинейных координат в любой точке М из области определения криволинейных координат. В ней функции (3.2) взаимно однозначны и взаимно непрерывно дифференцируемы. Компоненты векторов базиса записаны в декартовом базисе. Каждый вектор базиса касается соответствующей координатной линии, вдоль которой в (3.2) изменяется только одна координата, а две другие фиксированы. Длины векторов базиса hi (коэффициенты Ламе) могут быть для разных точек М различными и вычисляются по формулам: (3.3) Координатные поверхности, проходящие через точку М, определяются уравнениями При этом координатные поверхности пересекаются по координатным линиям, проходящим через точку М. Базис единичный, нормированный базис. Криволинейная система координат называется ортогональной системой координат, если векторы базиса ортогональны: Ортонормированный базис ортогональной системы координат удовлетворяет условию: Цилиндрическая ортогональная система координат. Прямое отображение K: (3.4) Обратное отображение : (3.5) Коэффициенты Ламе: Ортонормированный базис в разложении по декартовому базису имеет вид: (3.6) Сферическая ортогональная система координат. Прямое отображение: Обратное отображение: Коэффициенты Ламе: Скорость и ускорение точки в ортонормированном базисе криволинейной системы координат определяются по движению точки в криволинейных координатах следующим образом: (3.7) (3.8) Компоненты вектора скорости и компоненты вектора ускорения в ортонормированном базисе криволинейных координат называются физическими компонентами и имеют обычную физическую размерность. Пример вычисления физических компонент векторов скорости и ускорения в цилиндрических координатах. Физические компоненты вектора скорости имеют по (3.7) значения: (3.9) Для компонент вектора ускорения вычислим сначала в базисе , а затем посчитаем векторы . Так как векторы записаны в декартовом базисе в виде (3.6), то получаем в этом базисе: Сравнивая эти векторы с векторами (2.6), получаем: Окончательно, по формуле (3.8) и тогда (3.10) Полярная система координат. Если в цилиндрических координатах положить z = 0 , то система координат называется полярной системой координат. Она описывает движение точки в одной плоскости. Для нее физические компоненты векторов скорости и ускорения имеют вид : (3.11) (3.12) Задача 3.1. Вычислить физические компоненты векторов скорости и ускорения в сферических координатах. Решение. Коэффициенты Ламе вычислим по (2.3): Ортонормированный базис , записанный в декартовом базисе, имеет вид: Физические компоненты вектора скорости есть: Вычислим вектор ускорения точки : (3.13) Сначала вычисляются скалярные величины а затем - векторы . Покажем, что векторы перпендикулярны к соответствующим векторам . Действительно: Отсюда можно сделать вывод о том, что каждый вектор раскладывается по двум векторам базиса с номерами, не совпадающими с номером i . Для вектора можно получить, что: Проверим это: Аналогичные вычисления приводят к результатам: Наконец, по формуле (2.13) вектор ускорения принимает следующий вид: Таким образом, компоненты вектора ускорения в ортонормированном базисе сферических координат запишутся в следующем виде: (3.14) Лекция 4. Центральные силы. Потенциальные силы, потенциальная энергия. Силы, имеющие осевую симметрию. Идеальные силы. В лекции 1 была показана связь движения точки с силами ее взаимодействия с другими телами. Именно характер сил влияет на возможность интегрирования дифференциальных уравнений движения точки и записи результатов интегрирования уравнений движения в виде теорем динамики точки в интегральной форме и законов сохранения. Рассмотрим ниже подробнее этот вопрос. Определение. Сила, вызывающая движение точки, называется центральной, если в любом положении точки линия действия силы проходит через неподвижную точку О (центр, полюс). По определению, вектор положения точки параллелен вектору силы . Определение. Элементарной работой силы на элементарном перемещении называется скаляр dА, равный скалярному произведению вектора силы и вектора элементарного перемещения : Определение. Сила называется идеальной, если в любом положении точки, совместимом со связями, и на любом элементарном перемещении, допустимом связями, элементарная работа силы равна нулю. Определение. Сила называется потенциальной силой, если её элементарная работа есть со знаком минус полный дифференциал некоторой скалярной функции U , зависящей от скалярных параметров, определяющих положение точки: (4.1) Функция U для данной силы называется ее потенциальной энергией. По определению (4.1), если сила есть векторная сумма потенциальных сил, то точка имеет потенциальную энергию, равную сумме потенциальных энергий всех сил. Определение. Если в евклидовом пространстве R3 для каждого положения материальной точки задана потенциальная сила, зависящая от параметров, задающих ее положение (от координат), то говорят, что в пространстве задано силовое поле. Вычисление потенциальных энергий потенциальных сил . Сила тяжести . В декартовых осях Oxyz , где ось Oy направлена по вертикали, Если принять, что U(O) = 0, то С = 0 , и (4.2) Сила гравитационного притяжения Центральная сила записана в базисе сферических координат. Тогда Принимаем, что U(∞)=0. Тогда С = 0 и (4.3) Сила упругой пружины , где есть удлинение (сжатие) пружины. Коэффициент - жесткость пружины. Сила зависит только от удлинения (сжатия) пружины, поэтому (4.4) Здесь dx есть элементарное удлинение пружины при растяжении. Теоремы динамики точки. Законы сохранения. Интегрирование дифференциальных уравнений движения представляет в общем случае существенные трудности. Однако, для некоторых типов взаимодействий (типов сил) результаты интегрирования дифференциальных уравнений движения могут быть легко предсказаны и сформулированы с помощью введения нескольких новых понятий. Докажем это. Определения. Импульс (количество движения) материальной точки есть вектор (4.5) Момент импульса (момент количества движения) точки относительно неподвижной точки О есть вектор (4.6) 3. Моментом импульса относительно оси называется скаляр - проекция на эту ось вектора : (4.7) Кинетическая энергия точки есть скаляр (4.8) Момент силы относительно точки О есть вектор (4.9) 6. Проекция вектора на ось Оz называется моментом силы относительно оси Oz: (4.10) 7. Работа силы на пути из положения в положение есть скаляр (4.11) Здесь - элементарное перемещение в некотором положении точки на пути. Если сила потенциальная сила, то работа силы на пути не зависит от формы пути и вычисляется как разность потенциальных энергий U точки в начале и в конце пути: (4.12) Теорема об изменении импульса точки . Из второго закона Ньютона следует дифференциальная форма теоремы об изменении импульса (4.13) Если главный вектор сил зависит либо от времени, либо от скорости, то (4.13) можно проинтегрировать на интервале времени [ , ] (4.14) Уравнения (4.14) есть интегральные формы теоремы об изменении импульса. Закон сохранения импульса точки. Если в (4.13) главный вектор всех сил = 0 , то имеет место закон сохранения импульса (4.15) Если в (4.13) равна нулю компонента силы по оси Оx, то сохраняется импульс точки в проекции на эту ось: (4.16) Теорема об изменении момента импульса (момента количества движения) точки. Используем определения (4.6) и (4.9). Тогда дифференциальная форма теоремы имеет вид: Действительно, (4.17) что и требовалось доказать. Здесь - главный вектор (сумма всех сил), а - главный момент (сумма моментов) всех сил. Закон сохранения момента импульса точки. 1. Если главный момент всех сил равен нулю относительно точки О, то из (4.17) следует закон сохранения момента импульса относительно этой точки: (4.18) Определение. Говорят, что система сил имеет осевую симметрию, если в любом положении движущейся точки линии действия сил расположены в плоскости, проходящей через эту точку и некоторую неподвижную ось (0z). Задача. Доказать, что главный момент системы сил, имеющих осевую симметрию относительно оси 0z, равен нулю относительно этой оси. 2. Если равна нулю проекция главного момента сил на ось Оz , то из (4.17) следует закон сохранения момента импульса относительно оси 0z: (4.19) Таким образом, закон сохранения момента импульса относительно оси имеет место тогда, когда система сил имеет относительно этой оси осевую симметрию. Теорема об изменении кинетической энергии точки. Все формы теоремы используются тогда, в качестве переменных выбирается скорость точки и какие – либо её положения. Все формы теоремы есть формы записи закона Ньютона или способ его интегрирования в переменных скорость – положение. Дифференциальные формы теоремы об изменении кинетической энергии . (4.20) Интегральная форма теоремы об изменении кинетической энергии. (4.21) Задача. Доказательство теорем (4.20) и (4.21) провести самостоятельно. Закон сохранения механической энергии. Если все работающие силы потенциальны, результатом интегрирования будет закон сохранения механической энергии E = T + U . (4.22) Задача 4.1. Кольцо массой m скользит по неподвижной гладкой проволоке, имеющей форму параболы , в вертикальной плоскости, в поле постоянной силы притяжения к Земле. Определить силу реакции проволоки в нижнем положении кольца, если в его начальном положении кольцо имело скорость . Решение. Покажем, как выглядит решение, если представить движение в декартовых координатах, а затем в естественной форме. В обоих случаях решение можно получить с помощью дифференциальных уравнений движения (1.4) или (3.9), добавив к ним уравнения связей. Однако вначале проанализируем тип сил, вызывающих движение точки. Сила тяжести есть потенциальная сила, имеющая потенциальную энергию (ось 0y направлена вертикально вверх), а сила реакции гладкой проволоки есть идеальная сила – она не работает при движении точки, так как ее элементарная работа равна нулю в любом положении точки на траектории: В таком случае имеет место закон сохранения механической энергии (4.22), из которого можно найти скорость точки в любом положении по известным начальным значениям положения и скорости точки. Именно знание скорости точки, как следует из уравнений движения, достаточно для нахождения силы реакции в любом ее положении. Еще раз подчеркнем, что закон сохранения механической энергии есть результат интегрирования уравнений ее движения. Решение задачи в декартовых координатах . 1. Уравнения связей: (4.1.1) Уравнения движения точки в нижнем положении с учетом уравнений связей (4.1.1) в этом положении (x = 0) имеют вид: Закон сохранения механической энергии: (4.1.2) откуда скорость в нижнем положении равна: Ответ: Решение задачи с помощью естественных уравнений движения: Проекция закона Ньютона на нормаль: (4.1.3) Вычисление радиуса кривизны параболы по формуле: дает значение: С учетом скорости из (4.1.2) и найденного значения , из (4.1.3) получаем для силы реакции тот же ответ. Любую задачу динамики точки можно решить, используя декартовы координаты, однако в некоторых задачах проще применять криволинейные координаты. Задача 4.2. Материальная точка М движется по гладкой внешней поверхности неподвижного прямого кругового конуса с вертикальной осью 0z и углом 2 его раствора. Найти силу реакции конуса N для любого положения точки, если в начальном положении точка получила горизонтальную скорость на расстоянии от вершины конуса 0. Решение: решим задачу в сферических координатах. Условие нахождения точки на конусе запишем в виде уравнений связей: Выберем за независимые координаты и . Интегрируя уравнение закона Ньютона в проекции на базисный вектор , получим: Силу реакции конуса N найдем из уравнения закона Ньютона в проекции на базисный вектор : , откуда Решим задачу 4.2 в цилиндрических координатах. Уравнения связи (условие нахождения точки на конусе): Так как для сил имеет место осевая симметрия относительно оси 0z,то имеет место закон сохранения момента импульса относительно оси 0z: Закон Ньютона в проекциях на направления базисных векторов и с использованием (2.14) запишется так: Исключив из двух уравнений, получаем: Наконец, с помощью найденной из закона сохранения момента импульса относительно оси 0z величины , находим силу реакции: Лекция 5. Движение материальной точки в центральном поле сил. Если материальная точка движется под действием силы притяжения или отталкивания от неподвижного центра 0 (центральная сила), то она сохраняет момент импульса относительно 0: (5.1) Тогда точка может двигаться только в плоскости, проходящей через 0 и перпендикулярной векторам начального состояния и . В таком случае для описания ее движения достаточно ввести полярные координаты и . Запишем (5.1) в виде: (5.2) Пусть центральная сила зависит от расcтояния r (полярная координата) между полюсом 0 и текущим положением точки, то есть проекция силы на есть (5.3) Тогда сила образует поле с потенциальной энергией U(r): (5.4) и выполняется закон сохранения механической энергии (5.5) С использованием законов сохранения (5.2) и (5.5) для нахождения движения точки (5.6) запишем (5.5) в виде: Сначала решаем задачу нахождения Интегрирование проведено при возрастании r. Затем ищем φ = φ(t): Траекторию точки найдем из формулы: (5.7) Траектории точки в гравитационном (ньютоновском) поле сил. Гравитационное поле есть центральное поле с силой притяжения и потенциальной энергией : где m есть масса точки, есть постоянная Гаусса (Gauss) неподвижного притягивающего центра. Интегрирование (5.7) при условии, что получим траекторию в виде: или (5.8) Это есть уравнение конических сечений с параметром p и эксцентриситетом e , определенные по формулам: Формулы Бинэ. Дифференциальное уравнение движения точки в полярных координатах в проекции на базисный вектор с помощью (5.2) можно записать в форме, предложенной Бинэ: (5.9) Для доказательства (5.9) достаточно использовать следующие соотношения: Если (5.9) принято называть второй формулой Бинэ, то первой формулой Бинэ называют выражение квадрата скорости точки в виде: . Покажем, что уравнение (5.9) удобно для нахождения траектории точки в центральном поле сил на примере нахождения траектории в гравитационном поле сил с потенциальной энергией Уравнение (5.9) примет вид: (5.10) Это линейное неоднородное уравнение второго порядка. Его решение есть сумма частного решения и общего решения однородного уравнения Тогда общее решение можно представить в виде: Множество его решений для различных значений параметров и есть различные траектории точки. Примем, что больше нуля, . Тогда решение примет вид: Это уравнение конического сечения. Здесь p есть параметр конического сечения, e есть эксцентриситет. Далее. Как и раньше, примем, что угол φ = 0, когда расстояние от точки до притягивающего центра минимально и равно rmin = r0 . Тогда уравнение конического сечения запишется так же как и (5.8): Если e < 1 , то кривая есть эллипс. При e = 0 кривая есть окружность. Если e = 1 , то кривая есть парабола, а если e > 1 , то кривая есть гипербола. Можно показать, что постоянное значение эксцентриситета и вид траектории определяется начальным состоянием точки - r0 и v0 в любом месте на траектории. Оценим эту зависимость при φ = 0 , когда величина расстояния до притягивающего центра 0 минимальна, радиальная скорость . Тогда полная скорость v = . Из закона сохранения момента импульса (5.2) следует: (5.11) Отсюда: при траектория есть эллипс, (5.12) при траектория есть окружность, (5.13) при траектория есть парабола, (5.14) и, наконец, при траектория есть гипербола. (5.15) Задача 5.1. Тело, моделируемое материальной точкой, запускается на высоте H над Землей радиуса R со скоростью , перпендикулярной местной вертикали. Какова должна быть величина скорости запуска тела, чтобы оно бесконечно удалилось от Земли? Сила гравитационного притяжения точки к Земле у поверхности Земли равна . Чему равны первая и вторая космические скорости точки на Земле ? Решение. Гравитационная сила, определяемая формулой (5.9), из условия, что на земле она равна силе тяжести, дает значение постоянной Гаусса, равное Поэтому, из формул (5.14) и (5.15) имеем следующее значение искомой скорости: . Из формулы (5.13) первая космическая скорость равна , а из формулы (5.14) вторая космическая скорость равна Траектории планет Солнечной системы. Законы Кеплера. Если принять за неподвижный центр притяжения Солнце, то гравитационная сила притяжение записывается так: (5.12) где постоянная Гаусса Солнца записывается через гравитационную постоянную Солнечной системы G и массу Солнца . Траектории планет – эллипсы, для которых Солнце находится в фокусе эллипса. Угол φ отсчитывается от перигелия – минимального расстояния планет от Солнца. Это первый закон Кеплера. Из (5.1) и (5.2) вытекает второй закон Кеплера, выраженный через секторную скорость (5.13) Здесь S(t) - площадь, заметаемая вектором за время t . Секторная скорость планет постоянна. Период τ обращения планеты – время полного прохождения траектории - находится из условия (a, b есть большая и малая полуоси эллипса соответственно) Поэтому третий закон Кеплера выражает общее свойство для всех планет Солнечной системы: (5.14) то есть отношение квадратов периодов планет τ2 к кубам их больших полуосей a3 есть постоянная величина для всех планет солнечной системы. Доказательство. Решение задач о движении планет использует следующие соотношения между параметрами эллипса: (5.15) Лекция 6. Модель «система материальных точек». Система материальных точек есть набор конечного числа точек N, с постоянными конечными массами, взаимодействующих между собой, а также с другими телами, не включенными в систему. Мерами взаимодействий являются главный вектор внешних сил системы и главный вектор внутренних сил взаимодействий системы: (6.1) Здесь есть главный вектор всех внешних сил взаимодействий точки с номером k, а есть главный вектор всех внутренних сил взаимодействий этой точки со всеми остальными точками системы. Дифференциальные уравнения движения системы точек. Это есть совокупность дифференциальных уравнений движения всех точек: (6.2) Система (6.2), записанная в выбранном базисе, имеет 3N скалярных уравнений, в которых число скалярных неизвестных (движение, силы) больше, чем число уравнений. Система (6.2) иногда незамкнута. Введем новые понятия для системы точек, и с их помощью опишем некоторые свойства движения и взаимодействия точек системы. Определения. Центр масс системы точек есть точка С, определяемая массами точек и их векторами положения (6.3) При движении системы центр масс имеет скорость и ускорение : (6.4) Здесь называют массой системы. Теоремы динамики системы материальных точек. Теорема о движении центра масс: (6.5) Определения. Импульс системы: (6.6) Момент импульса системы относительно неподвижной точки О (оси Oz): (6.7) Кинетическая энергия системы точек: (6.8) Теорема об изменении импульса: (6.9) Теорема об изменении момента импульса: (6.10) Здесь есть главный момент всех внешних сил системы. Теорема об изменении кинетической энергии: (6.11) Законы сохранения. Закон сохранения вектора импульса системы или его проекции на ось. Если то (6.12) Если то Закон сохранения вектора положения центра масс или его проекции на ось Оx : Если , то Если , то (6.13) Закон сохранения вектора момента импульса или его проекции на ось: Если то (6.14) Закон сохранения механической энергии: если все работающие силы потенциальны, то (6.15) Задача 6.1. Призма 1 с массой может двигаться по гладкой горизонтальной поверхности. Гладкая призма 2 с массой скользит по гладкой боковой поверхности призмы 1 , образующей угол α с горизонтом. Найти общий класс движений системы двух призм, а также силы взаимодействий призм между собой и с горизонтальной плоскостью. Найти также величину перемещения призмы 1 за то время, когда призма 2 переместится вдоль боковой поверхности призмы 1 на расстояние . В начальный момент система призм покоилась. Решение 1 в декартовых координатах. Уравнения связей и число независимых геометрических параметров, определяющих положение системы двух точек 1 и 2. Шесть декартовых координат системы связаны четырьмя уравнениями связей: (6.1.1) Cистема двух точек имеет два независимых параметра. Пусть это будут x1 и x2 . Идеальность гладких поверхностей определяет внешнюю нормальную силу реакции и внутренние действие и противодействие внутреннего взаимодействия двух призм. Силы тяжести есть внешние активные силы (притяжения к Земле). Дифференциальные уравнения движения системы (6.2) в векторной форме: Дифференциальные уравнения движения системы в декартовых координатах Оxy, с учетом уравнения связи : (6.1.2) Четыре уравнения имеют четыре неизвестных . Решение этой системы имеет вид: Чтобы найти связь и , используем закон сохранения положения центра масс системы (6.13) в проекции на ось 0x: Решение 2. Применим к системе двух точек теорему о движении центра масс а затем напишем уравнение движения точки 2. Уравнения связей (6.1.1) и аксиомы сил те же, что в первом решении. Используем далее независимые параметры и , где Теорема о движении центра масс системы (6.5) в проекции на оси Ox и Oy имеет вид: Уравнение движения призмы 2 спроектируем на неподвижные оси и , перпендикулярную и параллельную наклонной плоскости призмы 2 соответственно: Решение четырех последних уравнений с четырьмя неизвестными дает те же результаты, однако уравнения решаются проще. Замечание. Если требуется найти только движение системы, то достаточно двух уравнений Ответ: движение системы в независимых параметрах и : Движение системы в декартовых координатах: Задача двух тел. Два твердых тела с массами m1 и m2 взаимодействуют между собой, причем модуль силы взаимодействия F(r) зависит от расстояния между телами r. Определить движение тел и их траектории, моделируя тела материальными точками. Решим задачу, предполагая, что существует инерциальная система отсчета, в которой есть декартова система координат Oxyz. Пусть и определяют в этой системе положения точек 1 и 2 соответственно. Так как учитывается только взаимодействие точек между собой, то, обозначая силу действия точки 1 на точку 2, а силу противодействия точки 2 на точку 1, дифференциальные уравнения движения системы запишем в виде: Система двух точек есть замкнутая система и от начальных условий, покоится или движется равномерно и прямолинейно, то есть его движение известно. Теорема. Решение задачи двух взаимодействующих точек в поле сил взаимодействия, зависящих от расстояния между ними, сводится к решению задачи движения одной точки с массой в том же поле центральной силы Доказательство. Умножая второе уравнение на , а первое уравнение - на , и вычитая из второго уравнения первое, получим следующее уравнение: (6.16) Это уравнение имеет такой же вид, а значит и такое же по форме решение, как уравнение движения точки 2 по отношению неподвижной точке 1, (5.3) - (5.9): Достаточно только в решении последнего уравнения заменить массу на приведенную массу . Окончательно, движение точек 1 и 2 определяется уравнениями в виде: Движение двух взаимодействующих точек в гравитационном поле. В гравитационном поле (5.10) уравнение движения точки1 по отношению к точке 2 имеет вид: (6.17) Решение этого уравнения есть движение точки 2 относительно подвижного центра притяжения 1, постоянная Гаусса которого равна (при неподвижном центре 1 она была равна ) Траектории обеих точек есть конические сечения с фокусом, расположенным в точке 1. Их геометрические параметры вычисляются так же, как в задаче с заменой массы на. Заметим, что все векторы записаны в одном и том же базисе инерциальной системы координат. Применение уравнения (6.17) к солнечной системе с заменой массы на массу приводит к уточненной формулировке законов Кеплера, с учетом движения Солнца. Они имеют ту же формулировку, как и в (5.13), (5.15), (5.17), только постоянную Гаусса в них необходимо заменить на где есть масса планеты. Траектории планет есть эллипсы, фокусы траекторий планет совпадают с Солнцем. Движение двух взаимодействующих точек в осях Кенига. Так как базис осей Кенига совпадает с базисом исходной инерциальной системы координат, а центр масс С движется равномерно и прямолинейно, то система координат Кенига с началом в центре масс инерциальна. По отношению к осям Кенига уравнения движения двух точек запишутся в виде: (6.18) Здесь и определяют движение точек 1 и 2 по отношению к системе координат Кенига, при этом Умножая второе уравнение (6.18) на , а первое - на и вычитая из второго уравнения первое, снова получим уравнение. После его решения движение точек в осях Кенига найдем из определения центра масс по формулам: Лекция 7. Модель «абсолютно твердое тело». Движение абсолютно твердого тела. По определению, расстояния между любыми двумя точками твердого тела не меняются, когда тело движется. Пусть в теле элементарная масса , занимает объём . Массовая плотность - масса единицы объёма, - есть . Выберем в теле систему координат для индивидуализации положения массы в теле вектором При движении твердого тела по отношению к неподвижной системе координат вектор вращается вместе с телом, и его запись в неподвижном базисе производится с помощью ортогональной матрицы вращения , сохраняющей расстояние между точками тела и ориентацию подвижного базиса. В неподвижном базисе вектор обозначим : (7.1) Движение твердого тела есть движение всех ее точек. Для любой точки тела определим ее движение в неподвижной системе координат как сумму двух векторов: и , определяющих соответственно поступательное и вращательное движение как составляющие абсолютного движения твердого тела: (7.2) Здесь есть ортогональная матрица перехода всех векторов, определенных в подвижном базисе, к неподвижному базису. Её определитель равен +1. Для таких матриц (7.2) обратная матрица равна транспонированной матрице : Задать движение твердого тела значит задать поступательную часть движения тремя координатами вектора полюса и тремя независимыми элементами матрицы вращения. Таким образом, произвольное движение задается 6 независимыми параметрами, то есть имеет 6 степеней свободы. Рассмотрим различные виды движений твердого тела и их уравнения связей, уменьшающие его число степеней свободы. Поступательное движение. Имеет 3 степени свободы из шести, так как элементы матрицы вращений постоянны, а движение задается Сферическое движение (вращение вокруг неподвижной точки О). Вращение тела вокруг неподвижной оси. В теле имеется две неподвижные точки. Тогда все точки оси (Оz) неподвижны. Нет поступательного движения, а вращательное движение задается одним параметром – углом поворота подвижных векторов базиса и вокруг неподвижной оси Оz . Ниже представим ограничения (связи) для других видов движения твердого тела. Скорости точек твердого тела. Угловая скорость тела. Скорость любой точки тела определим в неподвижном базисе: (7.3) Матрица At есть антисимметричная матрица, что доказывается с помощью (7.2): Тогда из (7.3) получим (7.4) Вектор можно представить следующим образом: так как где три различных элемента матрицы , по определению, образуют вектор угловой скорости твердого тела: Тогда скорость точки тела вычисляется как векторная сумма скорости поступательного движения с выбранным полюсом О и скорости вращательного движения по отношению к полюсу : (7.5) Вектор угловой скорости не зависит от выбора полюса О и определяется только матрицей вращения . Из (7.5) следует связь скоростей любых двух точек А и В тела: Итак: проекции скоростей любых двух точек твердого тела на направление вектора , соединяющего точки, равны. Кинематика частных движений твердого тела. Вращение тела вокруг неподвижной оси. Существуют хотя бы две точки тела, которые имеют нулевые скорости для любого момента времени. Тогда неподвижны в теле все точки, лежащие на оси, проходящей через эти неподвижные точки. Возьмем одну неподвижную точку за полюс О, а ось Оz проведем через другую неподвижную точку. Будем говорить, что твердое тело вращается вокруг неподвижной оси Оz. В матрице вращения и матрице есть угол вращения вокруг оси Оz подвижного базиса по отношению к неподвижному базису: откуда вектор угловой скорости имеет в неподвижном базисе одну ненулевую компоненту : (7.6) Во вращении твердого тела вокруг неподвижной оси вектор угловой скорости параллелен оси вращения . По (7.5) скорости точек тела перпендикулярны к оси вращения и к вектору . Точки тела движутся по окружностям с радиусами R и имеют величину 4. Плоское движение твердого тела. Скорость полюса расположена в неподвижной плоскости а угловая скорость перпендикулярна этой плоскости Плоское движение есть композиция поступательного и вращательного движений. Для двух точек А и В плоской фигуры скорости этих точек лежат в плоскости фигуры, а угловая скорость ей перпендикулярна. (7.7) Плоское движение имеет три степени свободы. Движение определяется уравнениями: Для непоступательного плоского движения твердого тела в любом положении тела существует точка Р плоской фигуры ( или ее продолжения), скорость которой равна нулю. Эту точку Р называют мгновенный центр скоростей плоской фигуры. Взяв её за полюс, из (7.7) получим, что скорость любой точки А плоской фигуры перпендикулярна вектору РА, соединяющего точку с мгновенным центром скоростей. Плоское качение цилиндра без проскальзывания по негладкой плоскости y = 0 . В общем случае положение твердого тела определяется шестью степенями свободы – тремя координатами полюса в теле, и тремя углами между осями неподвижной и подвижной осями координат. В данном примере шесть параметров связаны пятью уравнениями связей Условие качения без проскальзывания выражает первое уравнение. В нем для некоторой точки К на поверхности цилиндра принято, что в начальном положении она (К0) находилась в начале координат. Цилиндр имеет одну степень свободы. Ускорение точек твердого тела. Угловое ускорение тела. Продифференцируем по времени формулу (7.5): Здесь вектор называется угловым ускорением твердого тела. Итак, (7.8) Формула (7.8) задает поле ускорений в теле, то есть каждому вектору (или его образу ) сопоставляется вектор ускорения точки . Аналогично, формула (7.5) задает поле скоростей точек твердого тела. Абсолютная и относительная производные вектора, заданного в подвижной системе координат. Пусть некоторый вектор задан в подвижном базисе: Определения. Относительная производная вектора , заданного в подвижном базисе, есть (7.9) Абсолютная производная вектора, заданного в подвижном базисе, , есть (7.10) Тогда связь между ними в подвижном базисе имеет вид: (7.11) Здесь есть угловая скорость вращения подвижного базиса. Доказательство. Если вектор заданный в подвижном базисе, перезаписан в неподвижный базис, то абсолютная производная этого вектора в неподвижном базисе имеет вид: (7.12) Лекция 8. Кинематика сложного движения точки и твердого тела. Представить движение как сложное – это значит представить абсолютное движение как два движения – относительное плюс переносное. Сложное движение точки. Введем две системы отсчета: неподвижную (absolute) - с системой координат и подвижную - с системой координат . Определения. 1. Движение точки M по отношению к подвижной системе отсчета называется относительным (relative): (8.1) Относительная скорость и относительное ускорение есть: (8.2) 2. В каждый данный момент времени переносным (entraine) движением точки M называется движение той точки подвижной системы отсчета по отношению к неподвижной системе отсчета, в которой движущаяся точка в данный момент находится. (8.3) Переносная скорость, переносное ускорение есть: (8.4) Здесь есть матрица переносного вращения подвижной системы отсчета. 3. Абсолютным (absolute) движением называется движение точки по отношению к неподвижной системе координат: (8.5) Абсолютная скорость, абсолютное ускорение точки есть: (8.6) Теоремы сложения скоростей и ускорений в сложном движении точки. (8.7) (8.8) где последнее слагаемое есть ускорение Кориолиса (8.9) Доказательство. Сложное движение точки есть сумма двух движений: Теоремы докажем в неподвижном базисе. Переносные характеристики уже записаны в неподвижном базисе. Относительные характеристики, заданные в подвижном базисе, перезапишем в неподвижном базисе. Тогда по (7.12) получим: где Сложное движение твердого тела. В тех случаях, когда абсолютное движение твердого тела можно представить, как два движения, говорят о представлении движения твердого тела как сложное движение. Чтобы задать абсолютное движение, введем неподвижную, абсолютную систему координат . Тогда абсолютное движение тела определяется движением полюса О и матрицей абсолютного вращения . Введем подвижную систему координат , по отношению которой относительное движение тела определяется относительным движением полюса О и матрицей относительного вращения , а переносное движение задается вектором и матрицей . Наконец, для индивидуализации точек тела, как и раньше, задана в теле система координат , жестко связанная с телом. Исследуем только вращательные части относительного и переносного вращений, заданные матрицами и соответственно, игнорируя при этом все поступательные движения. Это значит, что начала всех систем координат совпадают, и точка О есть неподвижная точка тела. Тогда абсолютное вращение тела есть композиция двух последовательных аффинных преобразований с ортогональными матрицами. Поэтому определяется как произведение матриц и : Абсолютная скорость любой точки тела есть для сферического движения Здесь вектор последовательно перезаписывается сначала в подвижном базисе как , а потом в неподвижном как . Представляя движение тела как сложное, вычислим скорость точки так: Здесь , , есть угловые скорости абсолютного, относительного и переносного вращений соответственно. В результате получаем теорему о сложении векторов угловых скоростей относительного и переносного вращений: (8.10) Дифференцируя (8.10) по времени, докажем теорему о сложении угловых ускорений твердого тела в сложном движении: (8.11) Здесь , , и есть абсолютное, относительное и добавочное угловые ускорения.
|
|
|
|
|
|
|
|
|
|
|
|
Лекция 9. Динамика твердого тела.
Инерционные характеристики абсолютно твердого тела.
Масса тела, а также пространственное распределение элементарных масс в теле влияют на способность тела препятствовать ускорению или замедлению движения тела при его поступательном или вращательном движениях. Эти свойства называется инерционностью тела.
Определения.
Центр масс С есть постоянная в теле точка в подвижной системе координат 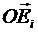
 (9.1)
(9.1)
Здесь вектор 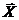 определяет в теле положение элементарной массы тела
определяет в теле положение элементарной массы тела  ,
, 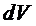 - её элементарный объем. Удельная массовая плотность
- её элементарный объем. Удельная массовая плотность 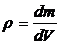 . Масса тела есть m .
. Масса тела есть m .
В неподвижной системе координат центр масс имеет положение
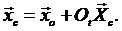
При движении тела центр масс движется и имеет в неподвижной системе координат скорость 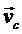 и ускорение
и ускорение  :
:
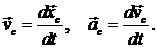 (9.2)
(9.2)
Импульс абсолютно твердого тела есть вектор
 (9.3)
(9.3)
Момент импульса телаотносительно неподвижной точки 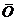 есть вектор:
есть вектор:
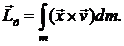 (9.4)
(9.4)
Кинетическая энергия твердого тела есть скаляр
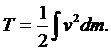 (9.5)
(9.5)
Дата добавления: 2018-04-04; просмотров: 289; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
