Критическая сила. Критическое напряжение. Гибкость. Влияние способов закрепления
Наименьшая величина сжимающей силы, при которой первоначальная форма равновесия стержня – прямолинейная становится неустойчивой – искривленной, называется критической.
При исследовании устойчивости форм равновесия упругих систем первые шаги были сделаныЭйлером.
В упругой стадии деформирования стержня при напряжениях, не превышающих предел пропорциональности, критическая сила вычисляется по формуле Эйлера: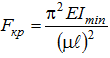 
гдеImin – минимальный момент инерции сечения стержня (обусловлено тем, что изгиб стержня происходит в плоскости с наименьшей жесткостью), однако исключения могут быть только в случаях, когда условия закрепления концов стержня различны в разных плоскостях, ℓ - геометрическая длина стержня, μ – коэффициент приведенной длиныиликоэффициент приведения (зависит от способов закрепления концов стержня), Значения μприведены под соответствующей схемой закрепления стержней 
Критическое напряжение вычисляется следующим образом
, где 
гибкость стержня ,
а 
радиус инерции сечения.
Введем понятие предельной гибкости.
Величинаλпред зависит только от вида материала: 
Если у стали 3 Е=2∙1011Па, а σпц=200МПа, то предельная гибкость
Для дерева (сосна, ель) предельная гибкость λпред=70, для чугуна λпред=80
Таким образом, для стержней большой гибкости λ≥λпред критическая сила определяется по формуле Эйлера.
В упругопластической стадии деформирования стержня, когда значение гибкости находится в диапазоне λ0≤λ≤λпр,(стержни средней гибкости) расчет проводится по эмпирическим формулам, например, можно использовать формулу Ясинского Ф.С. Значения введенных в нее параметров определены эмпирически для каждого материала.
|
|
|
σк=а-bλ, или Fкр=A(a—bλ)
где a и b – постоянные, определяемые экспериментальным путем (эмпирические коэффициенты).Так, для стали3 а=310МПа,b=1,14МПа.
При значениях гибкости стержня0≤λ≤λ0 (стержни малой гибкости) потеря устойчивости не наблюдается.
Таким образом, пределы применимости формулы Эйлера — применяется только в зоне упругих деформаций.
Формула Эйлера и пределы ее применимости для стальных и деревянных стержней. Другие формулы для определения критической силы
Для шарнирно закрепленного, центрально-сжатого стержня постоянного сечения (рис.8.2). I Формула Эйлера имеет вид:
где Е - модуль продольной упругости материала стержня;
Jmin - минимальный момент инерции поперечного сечения стержня.
Для стержней с другими видами закрепления формулу Эйлера записывают в виде:
где 
- приведенная длина стержня;
- коэффициент приведения длины.
|
|
|
Выражение "приведенная длина" означает, что в формуле Эйлера с помощью коэффициента все случаи закрепления концов стержня можно привести к основному, шарнирному закреплению.
Коэффициент приведения длины иногда можно оценить по числу полуволн n, по которым выпучится стержень, теряя устойчивость, а именно, можно принять
На рис. 8.2 показаны наиболее часто встречающиеся на практике случаи закрепления концов стержня и соответствующие им значения коэффициента
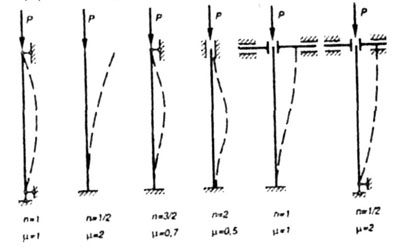
Рис. 8.2
Формула Эйлера применима только о пределах выполнения закона Гука, когда критическое напряжение 
не превышает предел пропорциональности материала стержня, так как эта формула была введена с помощью зависимости
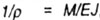
в свое время полученной на основании закона Гука.
Применимость формулы Эйлера можно определить, оценив гибкость стержня и сравнив эту гибкость с ее предельным значением. Гибкость стержня равна
где
- минимальный радиус инерции (геометрическая характеристика сечения);
- минимальный момент инерции площади сечения стержня.
Значение предельной гибкости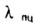 
получается из условия
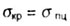
Предельная гибкость равна
Так, для малоуглеродистой стали, если принять Е = 2x105 МПа,
Для повышения несущей способности конструкций в них стремятся использовать стержни возможно меньшей гибкости. Так что расчет реальных конструкций с гибкостью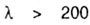 
практически маловероятен. Будем считать 
верхней границей значений гибкости реальных стержней.
|
|
|
Следовательно, формула Эйлера для определения критического значения сжимающей силы в виде
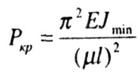
применима в случае, если гибкость стержня находится в пределах
(кривая СД на рис. 8.3)
Рис. 8.3
Для малоуглеродистой стали этот диапазон равен
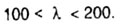
Дата добавления: 2018-04-04; просмотров: 4623; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!