Обозначение и правило знаков нормальных и касательных напряжений, действующих на гранях элементарного параллелепипеда в точке твердого тела. Закон парности касательных напряжений
Правило знаков нормальных напряжений: нормальное напряжение, соответствующее растяжению, считается положительным, а сжатию – отрицательным.
Правило знаков для касательных напряжений.
Касательное напряжение положительно, если одновременновыполняются (или одновременно не выполняются) два условия правила знаков касательных напряжений:
условие 1: направление напряжения совпадает с положительным направлением соответствующей координатной оси;
условие 2: внешняя нормаль к площадке, на которой возникает напряженное состояние, направлена в ту же сторону, что и другая соответствующая координатная ось.
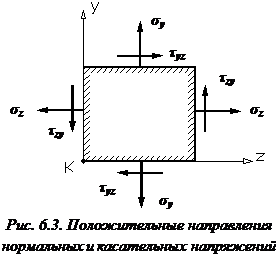
Например, все напряжения, возникающие по граням элементарного параллелепипеда (рис. 6.3), показаны положительными. Поскольку, как уже отмечалось в правиле знаков для касательных напряжений, во всех точках элементарного параллелепипеда напряженное состояние однородно, если одноименные напряжения, возникающие на параллельных гранях элемента, численно равны друг другу.
При анализе напряженного состояния в некоторой точке тела нормальные 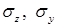 и касательные напряжения
и касательные напряжения 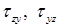 , возникающие по граням элементарного параллелепипеда, считаются заданными.
, возникающие по граням элементарного параллелепипеда, считаются заданными.

В формуле условии равновесия параллельного параллелепипеда в скобки заключены соответствующие силы, выраженные через касательные и нормальные напряжения, а их плечи указаны за скобками. После элементарных упрощений этого выражения, получим закон парности касательных напряжений:
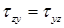
Формулировка закона парности касательных напряжений: касательные напряжения на любых двух взаимно перпендикулярных площадках, направленные по перпендикуляру к линии пересечения площадок, равны по величине, притом касательные напряжения либо сходятся к линии пересечения площадок, либо расходятся от нее.
Понятие о главных напряжениях и главных площадках. Понятие о наибольших касательных напряжениях
Главные площадки – это площадки, проходящие через исследуемую точку, на которых Касательные напряжения отсутствуют.
Главные напряжения – это возникающие на главных площадках нормальные напряжения
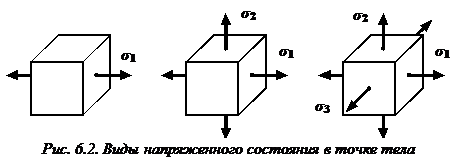
В общем случае нагружения (при объемном напряженном состоянии) среди множества площадок, проходящих через некоторую точку тела, всегда можно найти три взаимно перпендикулярныеглавные площадки. В окрестности любой точки деформированного твердого тела всегда можно выделить элементарный параллелепипед, ориентированный в пространстве таким образом, что по его граням будут возникать только нормальные (главные) напряжения (рис. 6.2).
Главные напряжения обозначаются 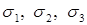 . Индексы расставляются после вычисления главных напряжений. Должно выполняться неравенство:
. Индексы расставляются после вычисления главных напряжений. Должно выполняться неравенство:
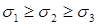
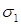 – наибольшее, а
– наибольшее, а 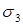 – наименьшее нормальное напряжение в исследуемой точке тела.
– наименьшее нормальное напряжение в исследуемой точке тела.
В частном случае нагружения может получиться так, что все три главных напряжения в исследуемой точке тела равны между собой. Тогда любая площадка, проведенная через эту точку, является главной площадкой.
По значениям главных напряжений дается оценка прочности материала в исследуемой точке деформированного твердого тела.
При плоском напряженном состоянии на грани элементарного параллелепипеда с нормалью х полностью отсутствует не только касательное, но и нормальное напряжение. Площадка тоже является главной площадкой, главное напряжение на которой равно нулю.
Формула для расчета касательных напряжений для балки квадратного сечения была получена в 1855 году русским инженером Д. И. Журавским,

где Qy — поперечная сила в сечении; Sx — статический момент отсеченной части относительно оси х, Sx = Аотсус, А0ТС – площадь поперечного сечения отсеченной части ; Jx — момент инерции сечения; b — ширина балки.
Наибольшее значение касательного напряжения достигается на нейтральной оси:
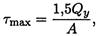
Дата добавления: 2018-04-04; просмотров: 1480; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
