Плоский изгиб (консольная балка)
Для балки, изображенной на рисунке 22, данные к эадаче приведены в таблице 7, необходимо:
1. Определить опорные реакции.
2. Написать выражения изгибающего момента М и поперечной
силы для Q каждого участка в общем виде.
3. Построить эпюры М и Q.
4. Подобрать балку круглого сечения из стали 20.
Таблица 7
Данные к задаче 4
| Номер | Схема | l | а1/ а | М | F | q |
| строки | По рис.5 | М | кНм | кН | кН/м | |
| 1 | 1 | 1,1 | 1 | 10 | 10 | 1 |
| 2 | 2 | 1,2 | 2 | 20 | 20 | 2 |
| 3 | 3 | 1,3 | 3 | 3 | 3 | 3 |
| 4 | 4 | 1,4 | 4 | 4 | 4 | 4 |
| 5 | 5 | 1,5 | 5 | 5 | 5 | 5 |
| 6 | 6 | 1,6 | 6 | 6 | 6 | 6 |
| 7 | 7 | 1,7 | 7 | 7 | 7 | 7 |
| 8 | 8 | 1,8 | 8 | 8 | 8 | 8 |
| 9 | 9 | 1,9 | 9 | 9 | 9 | 9 |
| 0 | 10 | 2 | 10 | 15 | 15 | 10 |
| Е | Д | Б | Г | В | Е |
Задача 5
Плоский изгиб (консольная балка). Определение перемещений
Используя результаты, полученные в задаче 6, для балки, изображенной на
рисунке 22, необходимо построить эпюру прогибов.
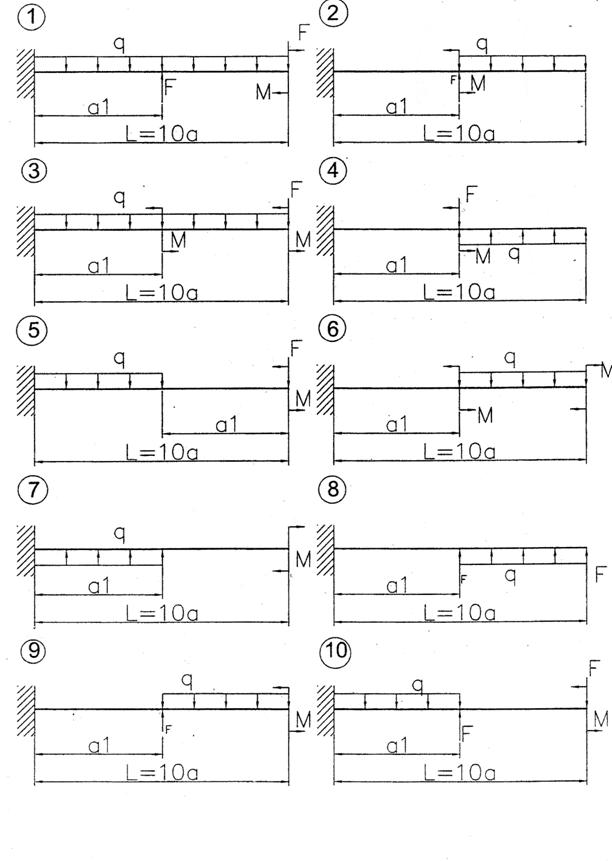
Рисунок 22 − Схемы балок к задаче 4
Задача 6
Плоский изгиб (двухопорная балка)
Для балки, изображенной на рисунке 23, необходимо:
1. Определить опорные реакции.
2. Написать выражения изгибающего момента М и поперечной силы Q для каждого участка в общем виде.
3. Построить эпюры М и Q.
4. Подобрать балку двутаврового поперечного сечения при [σ]=160 МПа.
|
|
|
Если по данным задачи опоры оказываются в одной точке, следует вместо
a1 взять 0,5 a1.
Таблица 8
Данные к задаче 8
| Номер | Схема | l | a1 /а | a2 /а | M | F | q |
| строки | по рис. 6 | м | кНм | кН | кН/м | ||
| 1 | 1 | 6 | 1 | 9 | 10 | 10 | 1 |
| 2 | 2 | 7 | 2 | 8 | 20 | 20 | 2 |
| 3 | 3 | 3 | 3 | 7 | 3 | 3 | 3 |
| 4 | 4 | 4 | 4 | 6 | 4 | 4 | 4 |
| 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| 0 | 10 | 10 | 10 | 10 | 15 | 15 | 10 |
| Е | Д | Б | В | Г | Д | Е |
Задача 7
Плоский изгиб (двухопорная балка). Определение перемещений
Используя результаты, полученные в задаче 8, для балки,
изображенной на рисунке 23, необходимо построить эпюру прогибов.
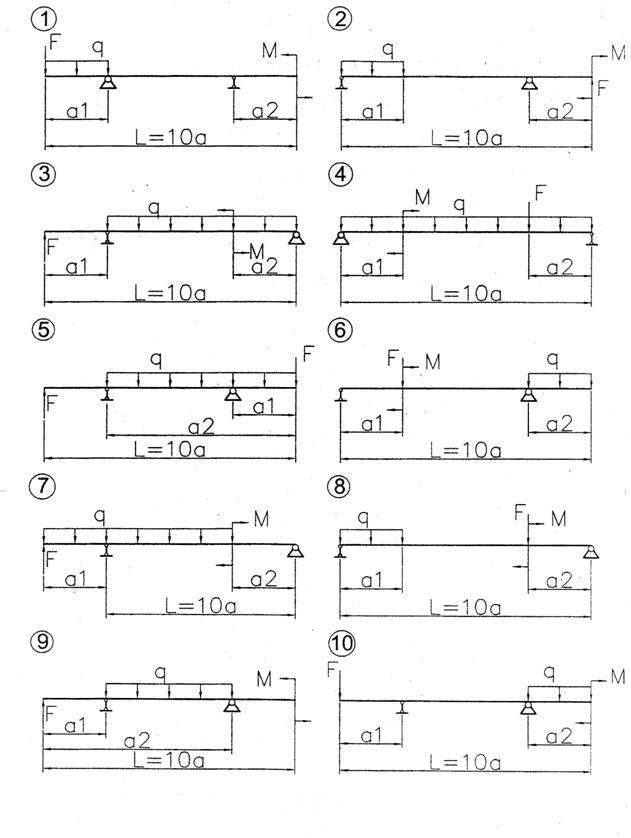
Рисунок 23 − Схемы балок к задаче 6
РАСЧЕТ НА ПРОЧНОСТЬ СТАТИЧЕСКИ
НЕОПРЕДЕЛИМОЙ БАЛКИ
Понятие о статически неопределимой системе
Статически неопределимой называется система, в которой реакции и внутренние усилия не могут быть найдены только из уравнений равновесия и определяются из дополнительных уравнений, вытекающих из деформированного состояния системы. Статически неопределимые системы имеют так называемые "лишние" связи: внешние (опорные) или внутренние. Будем рассматривать только внешние статически неопределимые системы. Степень статической неопределимости определяется разностью между числом неизвестных реакций и числом независимых уравнений статики. Будем рассматривать геометрически неизменяемые балки, не содержащие шарниров.
|
|
|
Обозначим:
n - степень статической неопределимости,
s - число опорных связей.
Для неподвижного закрепления плоеной геометрически неизменяемой системы требуется три определенным образом расположенные опорные связи. Число независимых уравнений статики для плоской системы равно трём. Следовательно, степень статической неопределимости такой системы может быть определена по формуле
n = s – 3
Например, для балки, изображённой на рисунке 24, а, число опорных cвязей s = 4 и, следовательно, степень статической неопределимости n= 4 — 3 = 1; для балок, изображенных на рисунке 24, 6 и на рисунке 24, в, степени статической неопределимости равны n= 2 и n= 4 соответственно.
|
|
|
Рисунок 24 − Определение степени статической неопределимости n
Для раскрытия статической неопределимости к уравнениям статики нужно составить столько дополнительных уравнений, сколько раз статически неопределима система. Эти дополнительные уравнения составляются из условий совместности деформаций.
Расчет статически неопределимой системы сводится к определению неизвестных реакций и построению эпюр внутренних усилий (изгибающих моментов М и попеpeчных сил Q, на основании которых подбираются размеры попеpeчных сечений или проверяются напряжения в опасных сечениях.
Существуют различные методы раскрытия статической неопределимости: метод сравнения перемещений, метод сил, метод перемещений. Рассмотрим метод сравнения перемещений.
Метод сравнения перемещений
Метод сравнения перемещений (деформаций) наиболее простой. Суть этого метода заключается в том, что дополнительные уравнения составляются из условий равенства нулю прогибов на опорах балки. Рассмотрим этот метод на примере.
|
|
|
Пример 6
Для балки, изображённой на рисунке 25, требуется определить опорные реакции и построить эпюры поперечных сил Qy и изгибающих моментов МZ
Рисунок 25 − Расчетная схема статически неопределимой балки
Балка имеет 4 опорные связи и является один раз статически неопределимой. Для определения неизвестных реакций МА, RА, HА и RB имеем только три уравнения равновесия статики:
1. ∑Х = 0; (11)
откуда следует, что HА = 0.
2. ∑Y = 0; (12)
RА − q∙3+ RB − F = 0;
RА + RB = 380.
3. ∑ МB = 0; (13)
МА + 6∙ RА − q∙3∙4,5 + M + F∙2 = 0;
МА + 6∙ RА = 1310.
Дополнительное четвертое уравнение составим, исходя из условия, что на опоре В прогиб yB равен нулю. Прогиб в опоре определим, используя универсальное уравнение упругой линии (метод начальных параметров), которое применительно к данной задаче имеет вид:
4. EI yB = 0; (14)
EI yB = EI y0 + EIφ0 ∙x + МА ∙62 /2 + RА ∙63 /6 − q∙64 /24 + q∙34 /24 + М ∙12 /2 = 0.
Так как качало координат помещено в защемлении, начальные параметры y0 = 0 и φ0 = 0, где y0 − прогиб балки при х = 0, φ0 − угол поворота сечения балки при х = 0.
С учетом этого уравнение (14) имеет вид
МА + 2∙ RА = 330.
Решая совместно уравнения (3) и (4), получим:
,
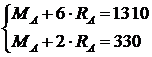- откуда RА = 245 кН, МА = − 160 кHм.
Затем, подставив в уравнение (12) найденное значение реакции RА, определим реакцию RB = 380 – 245 = 135 кН.
Для проверки правильности вычисленных реакций составим уравнение
моментов всех сил относительно опоры А:
∑ mА = −120∙3∙1,5 + 270 −135∙6 + 20∙8 = 0
Равенство нулю суммы моментов означает, что реакции определены
правильно. Определив значения реакций МА, RА, и RB, можно приступить к
построению эпюр внутренних усилий.
На рисунке 26 приведены: схема балки, эпюры поперечных сил
Qy, кН и изгибающих моментов МZ, кНм.
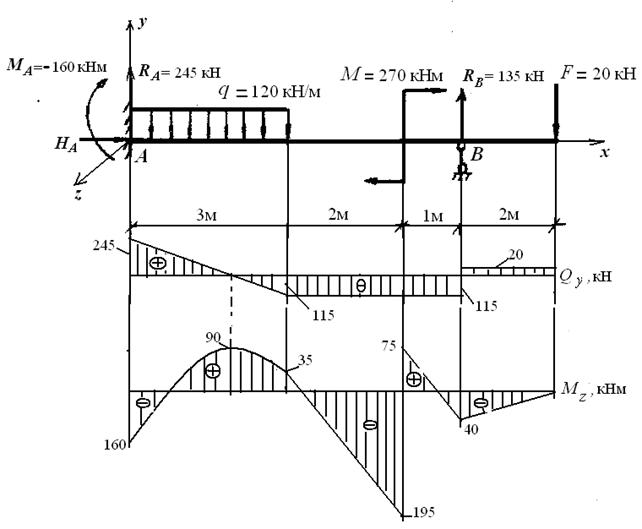
Рисунок 26 − Расчет статически неопределимой балки.
Эпюры поперечных сил Qy и изгибающих моментов МZ
Рассмотрим ещё один пример расчета статически неопределимой балки.
Пример 7
Определить размеры h, b прямоугольного поперечного сечения стальной балки (рисунок 27), если [σи] = 160 МПа, E = 2·105 МПа и h/b = 2. Определить прогибы посредине пролета балки и на конце консоли. Число неизвестных реакций 4, уравнений статики 3: балка один раз статически неопределима. Целесообразные уравнения статики:
;
. (15)
Рисунок 27 − Расчетная схема статически неопределимой балки
Число неизвестных реакций 4, уравнений статики 3: балка один раз статически неопределима. Целесообразные уравнения статики:
;
. (15)
Дополнительное уравнение составим, исходя из условия, что на опоре Bпрогиб равен нулю:
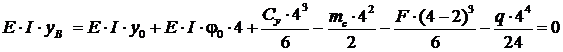. Так как начало координат помещено в защемлении, начальные параметры y0 = 0 и φ0 = 0. Тогда из уравнения прогибов получим:
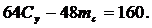(16)
Из уравнений (15) и (16) следует: Су = 7,75 кН, mc = 7 кН∙м.
Определим опорную реакцию B:
,
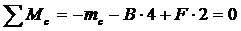откуда В = 4,25 кН.
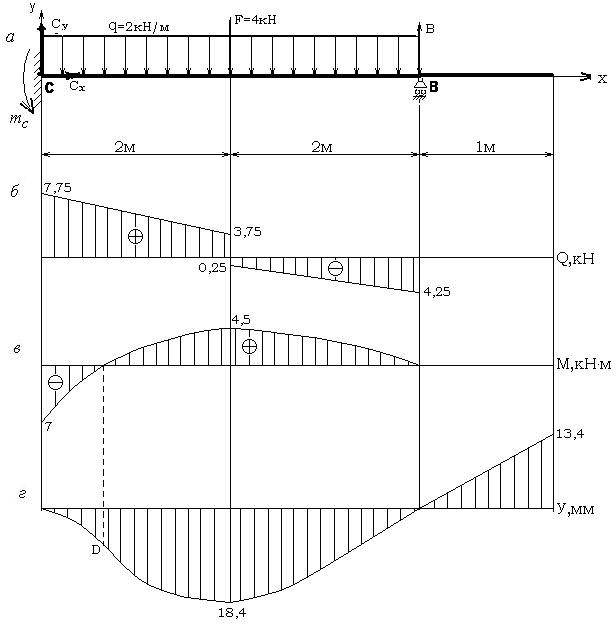
Рисунок 28 − Пример 9. Эпюры поперечных сил Q,
изгибающих моментов M и прогибов y
Проверка вычислений реакций:
.
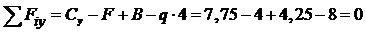Эпюры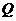 
и 
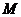показаны на рисунке 51, б, в.
Размеры сечения балки определим из условия прочности по нормальным напряжениям:
; 
;
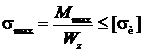Момент инерции сечения
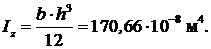
Жесткость сечения
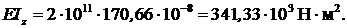
Прогиб посередине пролета балки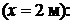 
;
.
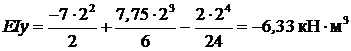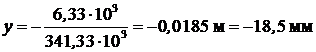Прогиб на конце консоли (х = 5 м):
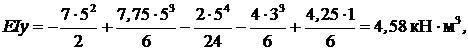
откуда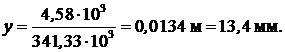 
Изогнутая ось балки показана на рисунке 51, г. Необходимо отметить,
что консольная часть балки не деформируется 
, но перемещается за счет деформации пролетной части. Точка D – точка перегиба упругой линии.
Задача 8
Дата добавления: 2018-04-04; просмотров: 1125; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!