Задачи для самостоятельного решения
Математика 8 класс. Контрольная работа №3
ДЕЛЕНИЕ МНОГОЧЛЕНОВ. МЕТОД ВЫДЕЛЕНИЯ ЦЕЛОЙ ЧАСТИ
Составитель: Г.А.Одинцова
Многочленом степени n от переменной х будем называть выражение вида
а0 хn +a1 xn-1+…+an-1 x +an, где n – целое неотрицательное число, а0 ,a1, …, an – действительные числа, причем а0¹0.
Например, 5х3 – х + 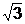 - многочлен степени 3, число -7 – многочлен степени 0.
- многочлен степени 3, число -7 – многочлен степени 0.
Обозначать многочлены принято символами P(x), Q(x), R1(x), R2(x), …, Rk(x) и т.д. Числа а0 ,a1, …, an будем называть коэффициентами многочлена, причем а0 – старшим коэффициентом, an –свободным членом. Например, числа 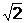 , -1, 0, -5 – коэффициенты многочлена P(x)=
, -1, 0, -5 – коэффициенты многочлена P(x)= 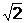 х3 – х2 -5, причем
х3 – х2 -5, причем 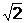 - старший коэффициент, -5 – свободный член.
- старший коэффициент, -5 – свободный член.
Многочлены принято записывать, располагая их члены по убыванию степени переменной. Такой вид называется стандартным или каноническим. Например, многочлен Q(x)= х – 2х2 + 3х3 – 1,5 следует записать в виде Q(x)=3х3 – 2х2 +х -1,5.
Многочлены, как и другие алгебраические выражения, можно складывать, вычитать и умножать по правилам раскрытия скобок и приведения подобных членов, известным вам с седьмого класса.
Пример 1. P(x)= х-1, Q(x)=х3+х2+х+1, P(x)+Q(x)=(х-1)+(х3+х2+х+1) = х3+х2+2х, P(x)-Q(x)=(х-1)-(х3+х2+х+1)=-х3-х2-2, P(x)×Q(x)=(х-1)(х3+х2+х+1)=х4+х3+х2+х+1-х3-х2–х-1= =х4-1.
Делить многочлен на многочлен можно не всегда. Например, если P(x)=х2-1, Q(x)=х-1, то P(x):Q(x)=х+1, т.е. деление возможно. А если P(x)=2, Q(x)=х, то P(x):Q(x)= 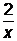 - не многочлен, т.е. деление невозможно. Но целое число p тоже не всегда можно разделить на целое число s нацело. Но можно всегда разделить с остатком, т.е. представить в виде p=sq+r, где 0£r<|s|. Например, 25=4×6+1, 25=(-4)×(-6)+1.
- не многочлен, т.е. деление невозможно. Но целое число p тоже не всегда можно разделить на целое число s нацело. Но можно всегда разделить с остатком, т.е. представить в виде p=sq+r, где 0£r<|s|. Например, 25=4×6+1, 25=(-4)×(-6)+1.
|
|
|
Попробуем получить аналогичное представление для многочленов, используя схему деления «уголком» (при этом очень важно, чтобы многочлены были записаны в стандартном виде).
Пример 2.
_4х5 + 7х4 + 6х3 +3х + 1 | 2х3 + х2 +3
4х5 + 2х4 + 6х2 | 2х2 +2,5х +1,75
_5х4 + 6х3 – 6х2 +3х +1
5х4 +2,5х3 +7,5х
3,5х3 – 6х2-4,5х +1
3,5х3+1,75х2 +5,25
-7,75х2-4,5х-4,25
Степень многочлена R(x)= -7,75х2-4,5х-4,25 меньше степени делителя 2х3 + х2 +3, значит, R(x)- остаток, а Q(x)= 2х2 +2,5х +1,75 – неполное частное.
Получаем 4х5 + 7х4 + 6х3 +3х +1 = (2х3 + х2 +3)(2х2 +2,5х +1,75)+(-7,75х2-4,5х-4,25).
Пример 3.
_ х4 + 2х3 – 2х2 -5х -2 | х2 +3х +2
х4 + 3х3 + 2х2 | х2 -х -1
|
|
|
_ -х3 – 4х2 -5х -2
-х3 – 3х2 -2х
_– х2 -3х -2
– х2 -3х -2
0
Получили, что остаток равен 0, т.е. х4 + 2х3 – 2х2 -5х -2=(х2 +3х +2)( х2 -х -1).
Выражение вида 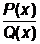 , где P(x) и Q(x) – многочлены, называют дробно-рациональным. Если степень P(x) выше степени Q(x), то часто бывает полезно выделить «целую часть». Например,
, где P(x) и Q(x) – многочлены, называют дробно-рациональным. Если степень P(x) выше степени Q(x), то часто бывает полезно выделить «целую часть». Например, 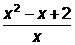 =
= 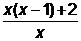 =х-1+
=х-1+ 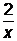 .
.
Рассмотрим ряд задач, решению которых помогает прием выделения целой части дробно-рационального выражения.
Задача 1. Найдите все целые числа с, при которых дробь 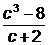 принимает целые значения.
принимает целые значения.
Решение: Выделим целую часть дроби 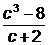 =
= 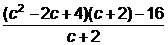 =с2-2с+4 -
=с2-2с+4 -  .
.
_с 3 – 8 | с+2
с3 + 2с2 | с2-2с +4 Дробь принимает целые значения, если с+2
_-2с2 -8 является делителем 16.
-2с2-4с Делители 16: ±1, ±2, ±4, ±8, ±16.
_-4с-8 Получаем с+2=1, с=-1; с+2=-1, с=-3; с+2=2, с=0;
|
|
|
-4с+8 с+2=-2, с=-4; с+2=4, с=2; с+2=-4, с=-6; с+2=8, с=6;
-16 с+2=-8, с= -10; с+2=16, с=14; с+2=-16, с=-18.
Ответ: -18, -10, -6, -4, -3, -1, 0, 2, 6, 14.
Задача 2. Зная, что 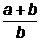 =7, найдите значение выражения
=7, найдите значение выражения 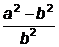 .
.
Решение: 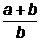 =7,
=7, 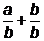 =7,
=7, 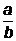 +1=7,
+1=7, 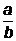 =6. Тогда
=6. Тогда 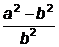 =
= 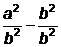 =
= 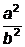 -1=36-1=35.
-1=36-1=35.
Ответ: 35.
Задача 3. Найдите значение выражения 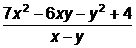 при х=6, у=129.
при х=6, у=129.
Решение: 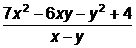 =
= 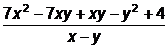 =
= 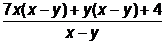 =7х+у+
=7х+у+ 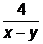 .
.
_7х2 – 6ху –у2 +4 | х-у
7х2 – 7ху | 7х+у При х=6 у= 129 получаем 42 +129 -4/123 = 170+119/123.
_ху - у2+4
ху - у2
+4
Ответ:170 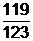 .
.
Задача 4. Найдите наименьшее значение дроби  , если х<1.
, если х<1.
Решение:  =
= 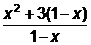 =3+
=3+ 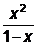 . При х<1 1-х>0 и
. При х<1 1-х>0 и 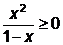 , значит, наименьшее значение выражения получим при
, значит, наименьшее значение выражения получим при 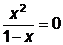 , т.е. при х=0, и это значение равно 3.
, т.е. при х=0, и это значение равно 3.
Ответ: 3.
Задача 5. Решите уравнение 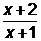 +
+ 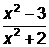 =2.
=2.
Решение: 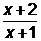 +
+ 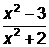 =2, 1+
=2, 1+ 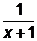 +1-
+1- 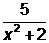 =2,
=2, 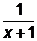 =
= 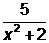 . По основному свойству пропорции при х¹-1 получаем х2 +2=5х+5 или х2 -5х -3=0, х=
. По основному свойству пропорции при х¹-1 получаем х2 +2=5х+5 или х2 -5х -3=0, х=  .
.
 Ответ: х=
Ответ: х=  .
.
Задача 6. Постройте график функции у= 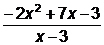 .
.
Решение:
_-2х2 +7х -3 | х-3
-2х2 +6х | -2х+1
_х-3
х-3
0
Получили у=-2х+1 при х¹3. Графиком функции
является прямая, на которой выколота точка с
|
|
|
координатами (3; -5).
Задача 7. Какое самое большое и самое маленькое значение принимает дробь 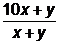 , если х и у – цифры, х¹0?
, если х и у – цифры, х¹0?
Решение: Применим к этому выражению метод выделения целой части дважды:
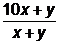 =1+
=1+ 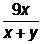 =1+
=1+ 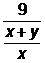 =1+
=1+ 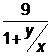 . Самое большое значение выражения будет при наименьшем значении знаменателя 1+
. Самое большое значение выражения будет при наименьшем значении знаменателя 1+ 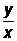 , т.е. при у=0. Это значение равно 10. Самое маленькое значение получим при самом большом значении
, т.е. при у=0. Это значение равно 10. Самое маленькое значение получим при самом большом значении 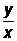 , т.е. при у=9,х=1. Это значение равно 1,9.
, т.е. при у=9,х=1. Это значение равно 1,9.
Ответ:10; 1,9.
Задачи для самостоятельного решения
Вариант 4.
1.Выполните деление многочленов с остатком:
а) х 5 –2х4 +4х3 -х2 +х+2 на х3 - 2х+1; б) х4 -2х2+1 на х2 +2х-1.
2.Найдите значение выражения 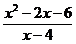 при х=34.
при х=34.
3.Определите, при каких целых n дробь 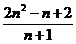 принимает натуральные значения.
принимает натуральные значения.
4.Найдите наименьшее значение дроби 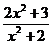 .
.
5.Постройте график функции у= 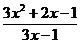 .
.
6.Зная, что 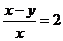 , найдите значение выражения
, найдите значение выражения 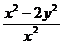 .
.
7.Решите уравнение 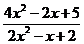 -
- 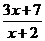 +1=0.
+1=0.
ПРИМЕЧАНИЕ: Срок отправки контрольной работы – 14 дней с момента получения.
Убедительно просим вкладывать вместе с ответами контрольной работы пустой конверт с маркой и подписанным вашим адресом! На конверте сделайте отметку: КЗШЕМН, математика, 8 класс, контрольная работа №3.
Выполненные контрольные работы отправляйте по адресу: 614022, г. Пермь, ул. Карпинского, д.79 или на электронную почту: region_olimp@mail.ru, контактный телефон: 8(342)280-11-03.
Дата добавления: 2018-02-28; просмотров: 312; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
