Дифференциальное уравнение теплопроводности. Решение задач теплопроводности связано с определением поля температур и тепловых потоков
Решение задач теплопроводности связано с определением поля температур и тепловых потоков. Для установления зависимости между величинами, характеризующими явление теплопроводности, используется метод математической физики, который рассматривает протекание физических процессов в произвольно выделенном из всего рассматриваемого пространства элементарном объеме и в течение бесконечно малого промежутка времени. Это позволяет пренебречь изменением некоторых величин и существенно упростить выкладки.
При выводе дифференциального уравнения теплопроводности принимаем некоторые допущения:
· считаем, что тело однородно и изотропно (то есть физические свойства тела не зависят от выбранного в нём направления),
· физические параметры λ, с(теплоемкость), и ρ (плотность) постоянны,
· деформация рассматриваемого объема, связанная с изменением температуры очень мала по сравнению с самим объемом
· внутренние источники теплоты равномерно распределены в теле.
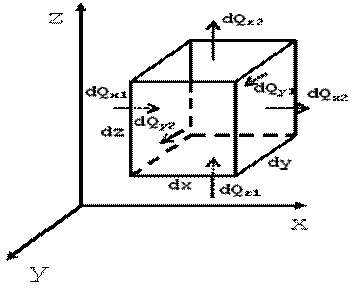
Рис. 2. Элементарный объем пространства (к выводу уравнения)
Под внутренними источниками теплоты понимаются тепловыделения, например, некоторый объем с тепловыми включениям (система отопления с замоноличенной в стене или полу трубой)
Внутренние источники теплоты характеризуются величиной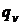 
— количеством теплоты, которое выделяется в единице объема в единицу времени.
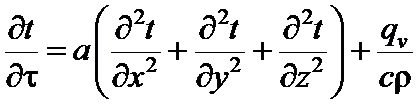(5)
Это уравнение называется дифференциальным уравнением теплопроводности или уравнением Фурье и лежит в основе математической теории теплопроводности. Величину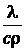 
называют коэффициентом температуропроводности и обозначают буквой a. Коэффициент температуропроводности a является физическим параметром вещества. Из уравнения (5) следует, что изменение температуры во времени для любой точки тела пропорционально величине a.
|
|
|
Сумма вторых частных производных любой функции в математическом анализе носит название оператора Лапласа и обозначается следующим образом:
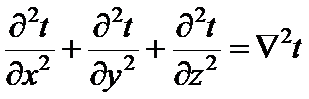
Поэтому уравнение (5) можно записать в виде:
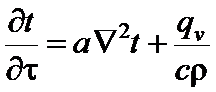(5а)
Методы решения дифференциального уравнения теплопроводности
Здесь Важно понимать !!!!
***** Обычная производная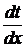 
и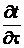 
отличаются тем, что для многомерного поля можно лишь расписать все в частных производных…
Дифференциальные уравнения теплопроводности не всегда могут быть легко решены точными аналитическими методами, т.к. они крайне сложны, поэтому на практике используют приближенными аналитическими методами, которые приводят к удовлетворительным для инженерной практики результатам. Приближенные методы решения задач применяются в случае, когда точные аналитические методы расчета затруднительны. Одним из приближенных методов и является численный метод – метод конечных разностей или метод сеток.
|
|
|
На практике часто интересуются распределением температур в двухмерных областях, т.е. когда температура изменяется только по двум координатам (например, угол здания, угол промышленной печи, изгиб детали, заготовки и т.д.). Знание такого распределения температур может помочь определить температурные напряжения, тепловые потоки.
Целью данной работы как раз является приобретение навыков расчета двумерных задач стационарной теплопроводности методом конечных разностей (методом сеток) и методом итераций.
Рис. 3. Схема упрощения общего дифференциального уравнения теплопроводности
Лекция 2
Дата добавления: 2018-02-28; просмотров: 304; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!