Пример. Рассмотрим примеры евклидовых пространств
 Арифметическое пространство
Арифметическое пространство 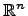 . Если
. Если 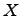 и
и 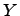 -- столбцы координат векторов
-- столбцы координат векторов 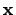 и
и 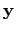 соответственно в стандартном базисе, то
соответственно в стандартном базисе, то 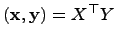 .
.
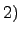 Пространство
Пространство 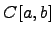 непрерывных функций на
непрерывных функций на 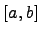 . Для любых двух функций
. Для любых двух функций 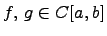 полагаем
полагаем 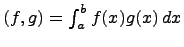 .
.
 Пространство многочленов степени не больше
Пространство многочленов степени не больше 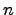 . Для любых двух многочленов
. Для любых двух многочленов 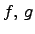 полагаем
полагаем 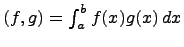 .
.
Определение. Пусть 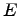 --
-- 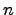 -мерное евклидово пространство с базисом
-мерное евклидово пространство с базисом 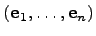 . Матрица Грамма базиса
. Матрица Грамма базиса 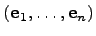 -- это матрица
-- это матрица

Определитель 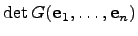 матрицы Грамма
матрицы Грамма 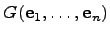 называется определителем Грамма.
называется определителем Грамма.
Определение. Вектора 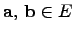 называются ортогональными, если
называются ортогональными, если 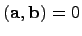 . Длинавектора
. Длинавектора 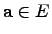 -- это неотрицательное число
-- это неотрицательное число  . Если
. Если 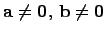 , то уголмежду
, то уголмежду 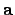 и
и 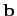 определяется по формуле
определяется по формуле 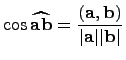 .
.
Теорема. Если векторы 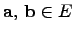 ортогональны, то
ортогональны, то  .
.
Теорема. Если  -- ортогональная система ненулевых векторов, то она линейно независима.
-- ортогональная система ненулевых векторов, то она линейно независима.
Теорема.[Неравенство Коши-Буняковского] Для любых векторов 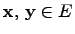 евклидова пространства
евклидова пространства 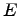 справедливо неравенство
справедливо неравенство 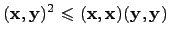 . Причем равенство имеет место тогда и только тогда, когда векторы
. Причем равенство имеет место тогда и только тогда, когда векторы 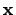 и
и 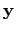 линейно зависимы.
линейно зависимы.
Следствие.[Неравенство Коши] Для всяких векторов чисел 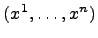 и
и  справедливо неравенство
справедливо неравенство 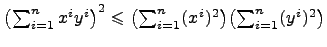 .
.
Следствие.[Неравенство Буняковского] Для любых чисел 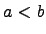 и любых непрерывных функций
и любых непрерывных функций 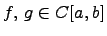 справедливо неравенство
справедливо неравенство 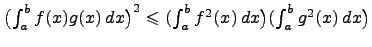 .
.
Следствие.[Неравенство треугольника] Для всяких векторов 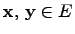 евклидова пространства
евклидова пространства 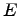 справедливо неравенство
справедливо неравенство 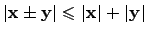 .
.
Определение. Унитарным пространством называется линейное пространство над полем комплексных чисел 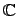 , на котором определена эрмитова положительно определенная функция. Она обозначается также
, на котором определена эрмитова положительно определенная функция. Она обозначается также  .
.
|
|
|
31. Ортогональные и ортонормированные базисы
Евклидово пространство является линейным пространством. Поэтому правомерно говорить о его размерности и его базисах.Как и произвольные линейные пространства, евклидовы пространства можно разделить на бесконечномерные и конечномерные.
Если базис евклидова пространства представляет собой ортогональную систему векторов, то этот базис называют ортогональным. В силу теоремы 3.4 любая ортогональная система ненулевых векторов линейно независима, и если она в п-мерном евклидовом пространстве состоит из пвекторов, то является базисом.
В линейном пространстве все базисы равноправны. В евклидовом же пространстве наличие скалярного умножения позволяет выделить среди всех базисов ортогональные и ортонормированные, которые более удобны и играют в линейной алгебре роль, аналогичную роли прямоугольной системы координат в аналитической геометрии.
Определение 3.7.Ортогональный базис называют ортонормированным, если каждый вектор этого базиса имеет норму (длину), равную единице.
Дополнительное требование к нормам векторов в ортонормированном базисе в принципе не является существенным, так как любой ортогональный базис легко преобразовать в ортонормированный, умножая векторы на соответствующие нормирующие коэффициенты (разделив каждый вектор базиса на его длину). Однако дополнительная нормировка векторов упрощает изложение теории.
|
|
|
32.Билинейной формой в действительном линейном пространстве  называется числовая функция
называется числовая функция 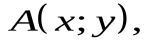 удовлетворяющая следующим двум условиям:
удовлетворяющая следующим двум условиям:
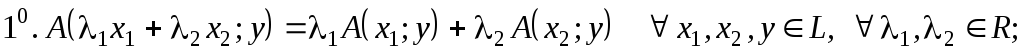

Билинейная форма  называется симметричной, если для любых векторов
называется симметричной, если для любых векторов 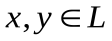 выполняется равенство
выполняется равенство
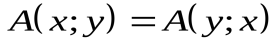 .
. 
Скалярное произведение 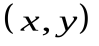 в евклидовом пространстве является примером симметричной билинейной формы.
в евклидовом пространстве является примером симметричной билинейной формы.
При заданном базисе 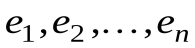 всякая билинейная форма в
всякая билинейная форма в  мерном действительном линейном пространстве
мерном действительном линейном пространстве  может быть записана в виде
может быть записана в виде
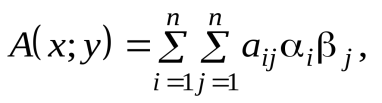

где 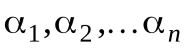 - координаты вектора
- координаты вектора 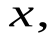 а
а 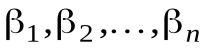 - координаты вектора
- координаты вектора 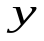 в данном базисе. Числа
в данном базисе. Числа 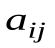 зависят от выбора базиса и вычисляются по формулам
зависят от выбора базиса и вычисляются по формулам

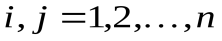
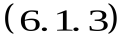
Матрица 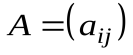 называется матрицей билинейной формы
называется матрицей билинейной формы  в базисе
в базисе 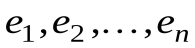 .
.
Дата добавления: 2018-02-28; просмотров: 303; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
