Понятие переключательной схемы

Раздел 4. Применение алгебры высказываний в логико-математической практике

Получение следствий из данных посылок

Мы знаем, как проверить, следует ли в логике высказываний некоторое предложение из других данных предложений.

Используя СКНФ, можно решить задачу о нахождении всех следствий из данных посылок. Будем иметь в виду следствия, содержащие только те элементарные высказывания, которые входят в посылки.

Чтобы получить всевозможные (неравносильные) следствия из данных посылок, можно применить следующее правило:

1) Составить конъюнкцию всех посылок (если они даны в форме высказываний, то предварительно их нужно формализовать).

2) Находим СКНФ.

3) Выписываем из СКНФ все возможные варианты комбинаций сомножителей ( , где n – количество этих сомножителей).

Пример 4.1: Найти все возможные следствия из посылок , .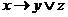

1) .

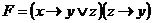2) .

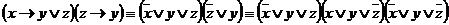3) Возможные следствия: , , , , , , .

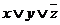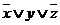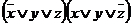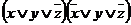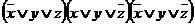Докажем, что любое из полученных выражений является следствием формулы F.

СКНФ истинна тогда и только тогда, когда каждый ее член является истинным. Следовательно, невозможны случаи, при которых СКНФ истинна, а какая-то из ее частей – ложна. Это и доказывает следование членов СКНФ и их конъюнкций из СКНФ формулы F.

Любая не тождественно истинная формула, не равносильная ни одной из полученных, не следует из данных посылок. Докажем это. Пусть  – формула, СКНФ которой содержит член , отличный от всех дизъюнкций, составляющих СКНФ конъюнкции  посылок. Утверждение, что  не следует из 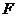, истинно, если существует такой набор значений переменных, при котором формула  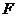истинна, а формула  ложна. Например, пусть 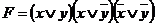,  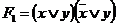и .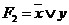

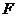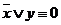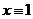Дизъюнкцию , входящую в формулу  и отличную от всех дизъюнкций, входящих в формулу , всегда можно сделать ложной, приписав переменным, входящим в эту дизъюнкцию без знака отрицания, значение «ложь», а переменным под знаком отрицания – значение «истина» (в нашем примере  при  и 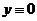). Формула  при этом также имеет значение 0, так как . Формула же 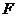 при этих значениях переменных примет значение 1, так как каждая из составляющих ее дизъюнкций содержит хотя бы один член, являющийся отрицанием члена дизъюнкции : для рассматриваемого примера имеем пр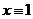и  и .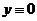

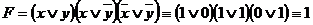Таким образом, всякая формула , СКНФ которой содержит дизъюнкцию, не входящую в СКНФ формулы 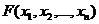, являющейся конъюнкцией посылок, не следует из этих посылок.

Замечание. Если стоит задача найти все следствия из данных посылок, но их количество велико, то перечисляют самые простые из полученных следствий, а для остальных указывают: «и их всевозможные конъюнкции».

 

Получение следствий, содержащих заданные переменные

Рассмотрим теперь задачу, в которой требуется найти не все следствия из данных посылок, а какое-нибудь одно, содержащее только некоторые заданные элементарные высказывания из числа входящих в посылки. Эту задачу можно решить с помощью СДНФ следующим образом:

1) Составляем объединенную таблицу истинности для формул, соответствующих посылкам.

2) Выделяем строки, в которых одновременно истинны все посылки.

3) В выделенных строках подчеркиваем значения переменных, которые должны войти в искомую формулу.

4) Если какие-нибудь наборы этих значений повторяются, вычеркнуть лишние.

5) Составляем СДНФ по выделенным строкам, учитывая только заданные переменные.

6) Упрощаем полученную СДНФ.

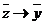Пример 4.2: Найти следствие из посылок  и , содержащее только переменные  и .

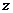Решение.

1) Составляем объединенную таблицу истинности посылок:

№ строки
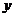
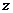
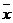
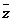
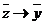
1	1	1	1	0	0	0	1	1
2	1	1	0	0	0	1	1	0
3	1	0	1	0	1	0	1	1
4	1	0	0	0	1	1	1	1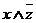
5	0	1	1	1	0	0	1	1
6	0	1	0	1	0	1	1	0
7	0	0	1	1	1	0	0	1
8	0	0	0	1	1	1	0	1

 

2) Выделяем строки, в которых обе посылки истинны. Это строки 1, 3, 4 и 5.

3) Подчеркиваем в отмеченных строках значения переменных  и .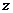

4) Вычеркиваем один из дважды встречающихся в отмеченных строках наборов значений переменных  и .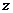

5) По оставшимся в отмеченных строках наборам значений  и 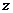 составляем СДНФ искомой формулы: .

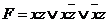6) Упростим полученную формулу:

.

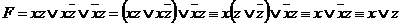Таким образом, 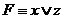 – искомое следствие.

Если посылки даны в виде содержательных предложений, то нужно: 1) формализовать их; 2) найти формулу искомого заключения; 3) перейти от формулы заключения к его содержательной форме.

Решение логических задач

К текстовым логическим задачам относят, как правило, те, при решении которых используются логические рассуждения, правила и методы. Все текстовые логические задачи можно условно разделить на три вида:

1. Задачи, в которых все высказывания истинны.

2. Задачи, в которых не все высказывания истинны, но мы точно знаем, какие из них истинны.

3. Задачи о «правдолюбцах» и «лжецах».

При решении любой задачи могут быть выделены следующие этапы:

1. Анализ условия задачи (выделение исходных данных).

2. Поиск метода решения.

3. Символическая запись задачи.

4. Рассуждения и пояснения к решению.

5. Анализ полученных результатов и запись ответа.

Среди методов решения текстовых логических задач чаще всего используют: метод рассуждений, метод таблиц, алгебраический метод (построение и упрощение формул).

Метод рассуждений. Идея метода: последовательные рассуждения и выводы из утверждений, содержащихся в условии задачи. Этим способом обычно решают несложные логические задачи. В методе рассуждений при решении помогают схемы, чертежи, краткие записи, умение выбирать информацию, умение использовать правило перебора.

Задача 1. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?

Решение. Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе – ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.

Ответ: Сергей изучает китайский язык, Михаил – японский, Вадим – арабский.

Задача 2. В поездке пятеро друзей – Антон, Борис, Вадим, Дима и Гриша, знакомились с попутчицей. Они предложили ей отгадать их фамилии, причём каждый из них высказал одно истинное и одно ложное утверждение:

Дима сказал: «Моя фамилия – Мишин, а фамилия Бориса – Хохлов». Антон сказал: «Мишин – это моя фамилия, а фамилия Вадима – Белкин». Борис сказал: «Фамилия Вадима – Тихонов, а моя фамилия – Мишин». Вадим сказал: «Моя фамилия – Белкин, а фамилия Гриши – Чехов». Гриша сказал: «Да, моя фамилия Чехов, а фамилия Антона – Тихонов». Какую фамилию носит каждый из друзей?

Решение. Обозначим высказывательную форму «юноша по имени А носит фамилию Б» как АБ, где буквы А и Б соответствуют начальным буквам имени и фамилии.

Зафиксируем высказывания каждого из друзей:

ДМ и БХ;

АМ и ВБ;

ВТ и БМ;

ВБ и ГЧ;

ГЧ и АТ.

Допустим сначала, что истинно ДМ. Но, если истинно ДМ, то у Антона и у Бориса должны быть другие фамилии, значит АМ и БМ ложно. Но если АМ и БМ ложны, то должны быть истинны ВБ и ВТ, но ВБ и ВТ одновременно истинными быть не могут.

Значит, остается другой случай: истинно БХ. Этот случай приводит к цепочке умозаключений: БХ истинно, БМ ложно, ВТ истинно, АТ ложно, ГЧ истинно, ВБ ложно, АМ истинно.

Ответ: Борис – Хохлов, Вадим – Тихонов, Гриша – Чехов, Антон – Мишин, Дима – Белкин.

С помощью таблиц решаются задачи, в которых устанавливается однозначное соответствие между элементами двух или трех множеств. При этом количество элементов во множествах может быть и неодинаковым. Таблица заполняется путем вычеркивания клеток, находящихся на пересечении столбцов и строк тех элементов разных множеств, между которыми точно нет соответствия. Оставшиеся невычеркнутыми клетки и соответствуют истинным высказываниям.

Задача 3. Барсук позвал к себе гостей:

Медведя, рысь и белку.

И подарили барсуку

Подсвечник и тарелку.

Когда же он позвал к себе

Рысь, белку, мышку, волка,

То он в подарок получил

Подсвечник и иголку.

Им были вновь приглашены

Волк, мышка и овечка.

И получил в подарок он

Иголку и колечко.

Он снова пригласил овцу,

Медведя, волка, белку.

И подарили барсуку

Колечко и тарелку.

Нам срочно нужен ваш совет.

(На миг дела отбросьте.)

Хотим понять, какой предмет

Каким дарился гостем.

И кто из шестерых гостей

Явился без подарка?

Не можем мы сообразить,

Сидим… Мудрим… Запарка…

Решение. В задаче устанавливается однозначное соответствие между множеством гостей (6 элементов) и множеством подарков (4 элемента). При этом все высказывания истинны. Поэтому составим таблицу 4х6:

	Медведь	Рысь	Белка	Мышка	Волк	Овечка
Подсвечник
Иголка
Тарелка
Колечко

Таблицу заполняем, вычеркивая клетки, которые соответствуют подаркам, которые данный гость НЕ дарил.

Из первого четверостишия ясно, что гости Медведь, Рысь и Белка подарили Подсвечник и Тарелку, значит, они НЕ дарили Иголку и Колечко. Вычеркнем соответствующие клетки в таблице:

	Медведь	Рысь	Белка	Мышка	Волк	Овечка
Подсвечник
Иголка	-	-	-
Тарелка
Колечко	-	-	-

Из второго четверостишия выясняем, что гости Рысь, Белка, Мышка и Волк НЕ дарили Колечко и Тарелку:

	Медведь	Рысь	Белка	Мышка	Волк	Овечка
Подсвечник
Иголка	-	-	-
Тарелка		-	-	-	-
Колечко	-	-	-	-	-

Аналогично рассуждая, из третьего четверостишия получаем:

	Медведь	Рысь	Белка	Мышка	Волк	Овечка
Подсвечник				-	-	-
Иголка	-	-	-
Тарелка		-	-	-	-	-
Колечко	-	-	-	-	-

И, из четвертого четверостишия:

	Медведь	Рысь	Белка	Мышка	Волк	Овечка
Подсвечник	-		-	-	-	-
Иголка	-	-	-		-	-
Тарелка		-	-	-	-	-
Колечко	-	-	-	-	-

Теперь, по оставшимся пустыми клеткам, можно сделать вывод: Медведь подарил тарелку, Рысь подарила подсвечник, Мышка подарила иголку и Овечка подарила колечко. Ничего не подарили Волк и Белка.

Задача 4. Владимир, Игорь и Сергей преподают математику, физику и литературу, а живут они в Рязани, Туле и Ярославле. Известно также, что Владимир живет не в Рязани, Игорь живет не в Туле, рязанец – не физик, Игорь – не математик, туляк преподает литературу. Кто где живет и что преподает?

Решение. В задаче устанавливается взаимно-однозначное соответствие между элементами трех множеств: имен (3 элемента), городов (3 элемента) и учебных предметов (3 элемента). При этом каждому элементу любого множества соответствует единственный элемент любого другого множества. Поэтому если мы установим соответствие между двумя любыми элементами двух разных множеств, то остальные связи этих элементов в этих множествах можно сразу вычеркнуть. Это существенно облегчает процесс решения.

Для таблицы выберем любые два множества. Например, множество имен и множество городов:

	Рязань	Тула	Ярославль
Владимир
Игорь
Сергей

Так как Владимир живет не в Рязани, а Игорь живет не в Туле, то в соответствующих клетках можно поставить знак минус:

	Рязань	Тула	Ярославль
Владимир	-
Игорь		-
Сергей

Так как туляк преподает литературу, то в соответствующем столбике во всех клетках напишем слово «литература».

	Рязань	Тула	Ярославль
Владимир	-	литература
Игорь		- литература
Сергей		литература

Из того, что туляк преподает литературу и того, что рязанец – не физик, следует, что рязанец преподает математику, соответственно физику преподает тот, кто живет в Ярославле. Добавим в таблицу соответствующую информацию:

	Рязань	Тула	Ярославль
Владимир	- математика	литература	физика
Игорь	математика	- литература	физика
Сергей	математика	литература	физика

Осталось не использованной информация о том, что Игорь – не математик. В соответствующей клетке ставим минус.

	Рязань	Тула	Ярославль
Владимир	- математика	литература	физика
Игорь	- математика	- литература	физика
Сергей	математика	литература	физика

Так как соответствие однозначное и в столбике «Рязань» в двух клетках из трех стоят минусы, то для этого столбца остается единственный положительный вариант против имени Сергей:

	Рязань	Тула	Ярославль
Владимир	- математика	литература	физика
Игорь	- математика	- литература	физика
Сергей	+ математика	литература	физика

Аналогично для строки «Игорь» единственным положительным вариантом является третья клетка. Все остальные клетки в строке «Сергей» и в столбце «Ярославль» можно вычеркнуть:

	Рязань	Тула	Ярославль
Владимир	- математика	литература	- физика
Игорь	- математика	- литература	+ физика
Сергей	+ математика	- литература	- физика

И теперь очевидным становится ответ: Владимир живет в Туле и преподает литературу, Игорь живет в Ярославле и преподает физику, Сергей – математик и живет в Рязани.

Алгебраический метод. При применении алгебраического метода самое трудное – перевести условие задачи на язык формул. Все остальное зависит от правильности выполнения преобразований, в процессе выполнения которых, как правило, сразу получается четкий, недвусмысленный ответ. Рассмотрим примеры.

Задача 5. Кросс осенний вспоминая,

Спорят белки два часа:

Победил в забег заяц.

А второй была лиса.

– Нет, – твердит другая белка, –

Ты мне эти штучки брось.

Заяц был вторым, конечно.

Первым был, я помню, – лось.

– Я, – промолвил филин важно, –

В спор чужой не стану лезть.

Но у вас в словах у каждой

По одной ошибке есть.

Белки фыркнули сердито.

Неприятно стало им.

Вы уж взвесьте все, найдите,

Кто был первым, кто вторым.

Решение. Для каждого из высказываний задачи, истинность которых устанавливается, введем обозначения.

Пусть А = «Первым был заяц»; В = «Второй была лиса»; С = «Заяц был вторым»; D = «Лось был первым». Тогда высказывание первой белки, учитывая, что истинна только одна его часть, примет вид: 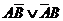. Соответственно, высказывание второй белки будет выглядеть так: 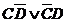. Оба высказывания обеих белок истинны, так как хотя бы одна из конъюнкий всякий раз истинна. Следовательно, будет истинна и конъюнкция . Упростим эту формулу.

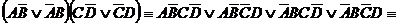
Заметим, что конъюнкци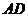и ,  и 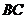 являются ложными, так как два зверя не могут одновременно занимать одно и то же призовое место и один зверь не может занимать два разных призовых места. Поэтому:

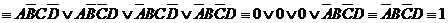
Отсюда следует, что заяц не был первым, лиса была второй, заяц не был вторым, лось был первым, а из этого вытекает, что заяц был третьим.

Ответ: Первый – лось, вторая – лиса.

Задача 6. В одном королевстве были незамужние принцессы, голодные тигры и приговоренный к казни узник. Но король всякому узнику, осужденному на смерть, давал последний шанс спастись. Ему предлагалось угадать, в какой из двух комнат находится тигр, а в какой принцесса. Хотя вполне могло быть, что король в обеих комнатах разместил принцесс или , что хуже, в обеих тигров. Выбор надо было сделать на основании табличек на дверях комнат. Причем, узнику было известно, что утверждения на табличках либо оба истинны, либо оба ложны. Надписи гласили: 1 комната: «По крайней мере в одной из этих комнат находится принцесса»; 2 комната: «Тигр в другой комнате». Какую дверь должен выбрать узник?

Решение. Введем обозначения: 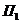 = «В первой комнате находится принцесса».  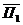= «В первой комнате находится тигр».  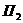= «Во второй комнате находится принцесса».  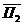= «Во второй комнате находится тигр». Тогда утверждение на первой двери: 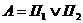, утверждение на второй двери: .

Условие задачи о том, что утверждения на табличках либо одновременно истинны, либо одновременно ложные, записываются так: .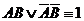

Подставим вместо А и В соответствующие формулы и упростим:

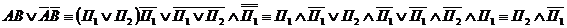
Таким образом, 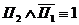. Значит, в первой комнате находится тигр, а во второй принцесса.

Понятие переключательной схемы

Переключательная схема – это устройство из переключателей (контактов) и проводов, связывающих два полюса – вход и выход. (Полюсов может быть и больше, но мы ограничимся рассмотрением двухполюсных схем.) Для конкретности будем говорить о переключательных схемах, представляющих собой участок электрической цепи, по которому проходит ток от источника А к потребителю В (например, к лампочке). Между источником и потребителем может быть замыкающий и размыкающий цепь контакт либо несколько контактов, соединенных последовательно или параллельно.

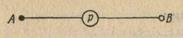Рассмотрим схему с одним контактом (рис.). Цепь замкнута (лампочка горит) в том и только в том случае, если контакт замкнут.

Сопоставим контакту р переменную X, а двум состояниям контакта "замкнут", разомкнут" – соответственно значения 1и0переменной X. Условимся также обозначать утверждение "цепь замкнута" через 1, а утверждение "цепь разомкнута" – через 0; тогда формула X опишет работу данной цепи:

 

 

р	X	Цепь
Замкнут	1	Замкнута
Разомкнут	0	Разомкнута

 

 

Если между источником и потребителем тока поместить два контакта р₁ и р₂ (рис.), соединенные последовательно, то цепь замкнута, когда оба контакта замкнуты, и разомкнута, когда хотя бы один из них разомкнут. Конъюнкция переменных Х и Y, поставленных в соответствие контактам р₁ и р₂, истинyа, когда обе переменные принимают значение 1, и ложна, когда хотя бы одна из них принимает значение 0. Таким образом, формула 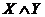 соответствует схеме на втором рисунке.

Очевидно, что формула  описывает схему с п последовательно соединенными контактами.

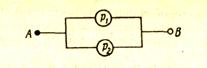Если контакты р₁ и р₂ соединены параллельно (рис.), то цепь замкнута, когда хотя бы один из контактов замкнут, и разомкнута когда оба они разомкнуты. Такой схеме соответствует формула 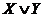, являющаяся истинной, когда хотя бы одна из переменных принимает значение 1, и ложной, когда обе переменные принимают значение 0.

Легко видеть, что дизъюнкция  описывает работу цепи с п параллельно соединенными контактами.

Контакты не всегда независимы друг от друга. Можно устроить их так, чтобы они замыкались и размыкались одновременно, либо так, чтобы один из них размыкался, когда другой замыкается, и наоборот. В первом случае контакты называются идентичными, во втором – инверсными. Идентичные контакты обозначают одинаково; контакт, инверсный контакту р, будем обозначать через 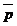. Если контакту р поставить в соответствие переменную X, то очевидно, что контакту  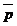будет соответствовать формула : Когда переменная X принимает значение 1(контакт р замкнут), формула  принимает значение 0(контакт 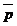 разомкнут), и наоборот.

Установленные соответствия дают возможность описать любую цепь с последовательно или параллельно соединенными контактами формулой логики высказываний. С другой стороны, любую формулу логики высказываний можно смоделировать в виде переключательной схемы.

 

---

Дата добавления: 2018-02-28; просмотров: 1128; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!