Раздел 4 Основы теории комплексных чисел. Тема 4.1 Понятие комплексного числа
Тема 4.1 Понятие комплексного числа. Действия над комплексными числами
Определение комплексного числа в алгебраической форме, действия над ними. Геометрическое изображение комплексных чисел. Решение алгебраических уравнений. Тригонометрическая форма комплексных чисел. Переход от алгебраической формы к тригонометрической и обратно. Действия над комплексными числами в тригонометрической форме. Показательная форма комплексных чисел, действия над ними. Тождество Эйлера
Литература
Основные источники:
1. Григорьев В.П., Дубинский Ю.А. Элементы высшей математики: учебник для студ. Учреждений сред. проф. образования. – М.:ИЦ «Академия», 2014
2. Григорьев В.П. Сборник задач по высшей математике: учеб. пособие для студ. учреждений сред.проф. образования. - М.:ИЦ «Академия», 2014
3. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика: учебник для студентов учреждений сред. проф. образования. – М., Издательский центр «Академия», 2015
Дополнительные источники:
4. Богомолов Н.В. Практические занятия по математике. Учеб. пособие для сред. учеб. заведений. – Москва, Издательство Юрайт, 2017
Интернет-ресурсы:
1. https://biblio-online.ru -сайт электронной библиотеки Юрайт
2. http://www.mathprofi.ru – сайт по решению задач высшей математики и математической библиотеки
Требования к оформлению контрольной работы
Контрольная работа выполняется студентом в отдельной тетради в клетку 12-ти или 18-ти листов. Титульный лист тетради заклеивается листом белой бумаги с напечатанным текстом (см. приложение №1). Работа студента должна быть выполнена чернилами одного (синего или фиолетового) цвета, аккуратно и разборчиво.
Решение задач желательно располагать в порядке номеров, указанных в задании, номера задач следует указывать перед условием.
Условия задач должны быть обязательно переписаны полностью.
При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения. Перечислим важнейшие из этих требований:
а) студенты должны соблюдать абзацы, всякую новую мысль следует начинать с красной строки;
б) важные формулы, равенства, определения нужно выделять в отдельные строки, чтобы сделать их более обозримыми;
в) при описании решения задачи краткая запись условия отделяется от решения и в конце решения ставится ответ.
г) серьезное внимание следует уделять правильному написанию сокращенных единиц величин;
д.) необходимо правильно употреблять математические символы.
Решения задач должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.
Чертежи следует выполнять карандашом с использованием чертежных инструментов, соблюдая масштаб.
Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки.
Контрольная работа состоит из восьми заданий. Вариант работы выбирается по последней цифре номера, под которым находится фамилия студента в списке на странице дисциплины в учебном журнале. Из всех задач студенту необходимо решить задачи под номерами, последняя цифра которых соответствует номеру варианта. Например, если у студента вариант №1, то он выполняет в полном объеме задачи №1, 11, 21, 31, 41, 51, 61, 71. Студент, имеющий вариант№10, выполняет задания №10, 20, 30, 40, 50, 60, 70, 80.
Задания для контрольной работы
1-10. Решить систему линейных уравнений:
а) методом Крамера;
б) матричным методом;
в) методом Гаусса.
| 1. | 
| 6. | 
| |
| 2. | 
| 7. | 
| |
| 3. | 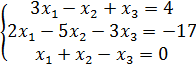
| 8. | 
| |
| 4. | 
| 9. | 
| |
| 5. | 
| 10. | 
|
11-20. Вычислить предел функции:
| 11. | а) | 
| б) | 
| в) | 
|
| 12. | а) | 
| б) | 
| в) | 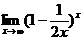
|
| 13. | а) | 
| б) | 
| в) | 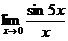
|
| 14. | а) | 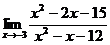
| б) | 
| в) | 
|
| 15. | а) | 
| б) | 
| в) | 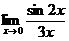
|
| 16. | а) | 
| б) | 
| в) | 
|
| 17. | а) | 
| б) | 
| в) | 
|
| 18. | а) | 
| б) | 
| в) | 
|
| 19. | а) | 
| б) | 
| в) | 
|
| 20. | а) | 
| б) | 
| в) | 
|
21-30. Вычислить производную данной функции:
|
21.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
22.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
23.
| а) | 
| в) | 
|
| б) | 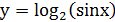
| г) | 
| |
|
24.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
25.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
26.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
27.
| а) | 
| в) | 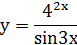
|
| б) | 
| г) | 
| |
|
28.
| а) | 
| в) | 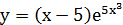
|
| б) | 
| г) | 
| |
|
29.
| а) | 
| в) | 
|
| б) | 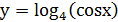
| г) | 
| |
|
30.
| а) | 
| в) | 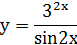
|
| б) | 
| г) | 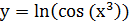
|
31-40. Исследовать функцию с помощью производной и построить её график.
| 31. | 
| 36. | 
| |
| 32. | 
| 37. | 
| |
| 33. | 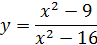
| 38. | 
| |
| 34. | 
| 39. | 
| |
| 35. | 
| 40. | 
|
41-50. Вычислить интеграл:
|
41.
| а) | 
| в) | 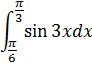
|
| б) | 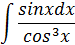
| г) | 
| |
|
42.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
43.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
44.
| а) | 
| в) | 
|
| б) | 
| г) | 
|
|
45.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
46.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
47.
| а) | 
| в) | 
|
| б) | 
| г) | 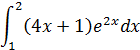
| |
|
48.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
49.
| а) | 
| в) | 
|
| б) | 
| г) | 
| |
|
50.
| а) | 
| в) | 
|
| б) | 
| г) | 
|
51-60. Найти общее решение дифференциального уравнения первого порядка:
| 51. | 
| 56. | 
| |
| 52. | 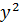 dy= dy=  dx dx
| 57. | 
| |
| 53. | 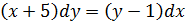
| 58. | 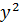 dy= dy=  dx dx
| |
| 54. | 
| 59. | 
| |
| 55. | 
| 60. | ydy= 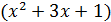 dx dx
|
| 61. | Из десяти билетов выигрышными являются 2. Определить вероятность того, что среди взятых наудачу 5 билетов один выигрышный. |
| 62. | Устройство содержит 5 элементов, из которых 2 изношены. При включении устройства включаются случайным образом 2 элемента. Найти вероятность того, что включенными окажутся неизношенные элементы. |
| 63. | Ребёнок играет с пятью буквами разрезанной азбуки а, к, р, ш, ы. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «крыша»? |
| 64. | В ящике содержится 100 деталей 10 из которых бракованы. Наудачу извлекают 4 детали. Найти вероятность того, что среди извлечённых деталей нет бракованных. |
| 65. | В книжной лотерее разыгрывается 6 книг. Всего в урне имеется 50 билетов. Первый подошедший к урне вынимает билет. Определить вероятность того, что билет окажется выигрышным. |
| 66. | В урне содержатся 5 синих, 7 красных и 8 белых шара. Из нее наудачу извлекаются сразу два шара. Найти вероятность того, что будут вынуты два белых шара. |
| 67. | В двух ящиках находятся детали: в первом – 20, из них 18 стандартных, во втором – 25, из них 3 – бракованных. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными. |
| 68. | Вероятность попадания в цель при стрельбе первого и второго орудий соответственно равны 0,98 и 0,95. Найти вероятность того, что при одновременном залпе из обоих орудий в цель попадут оба выстрела. |
| 69. | Для сигнализации о возгорании установлены два независимо работающих датчика. Вероятности того, что при возгорании датчик сработает, для первого и второго датчиков соответственно равны 0,98 и 0,95. Найти вероятность того, что при пожаре сработает ровно один датчик. |
| 70. | Для сигнализации о возгорании установлены два независимо работающих датчика. Вероятности того, что при возгорании датчик сработает, для первого и второго датчиков соответственно равны 0,98 и 0,95. Найти вероятность того, что при пожаре сработают оба датчика. |
71-80. Даны числа  и
и  Вычислить:
Вычислить:
а) сумму  ,
,
б) разность  ,
,
в) произведение  ,
,
г) частное  .
.
| 71. |  , ,
| 
| 76. |  , ,
| 
| |
| 72. |  , ,
| 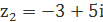
| 77. |  , ,
| 
| |
| 73. |  , ,
| 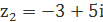
| 78. |  , ,
| 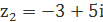
| |
| 74. |  , ,
| 
| 79. |  , ,
| 
| |
| 75. |  , ,
| 
| 80. |  , ,
| 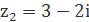
|
Вопросы для самоконтроля
1. Определение матрицы. Виды матриц: квадратная, треугольная, ступенчатая, единичная, нулевая, вектор-матрица (матрица-строка, матрица-столбец), транспонированная матрица.
2. Операции над матрицами, их свойства.
3. Минор элемента матрицы. Алгебраическое дополнение элемента матрицы.
4. Союзная матрица. Обратная матрица.
5. Определитель. Определитель второго и третьего порядка.
6. Определение СЛУ и СЛОУ.
7. Сущность метода определителей (правила Крамера) в решении СЛУ.
8. Сущность метода обратной матрицы в решении СЛУ.
9. Сущность метода Гаусса в решении СЛУ.
10. Определение предела. Свойства предела.
11. Определение бесконечно малой и бесконечно большой величины.
12. Замечательные пределы.
13. Односторонние пределы.
14. Определение функции, непрерывной в точке и на промежутке.
15. Определение точки разрыва функции. Классификация точек разрыва функции.
16. Определение производной. Формулы дифференцирования. Правила дифференцирования.
17. Геометрический и физический смысл производной.
18. Формулы дифференцирования сложной функции.
19. Производная второго порядка и её физический смысл.
20. Производная высшего порядка (n-ого порядка).
21. Правило Лопиталя по раскрытию неопределенностей вида 0/0 и ∞/∞.
22. Определение дифференциала. Геометрический смысл дифференциала.
23. Дифференциал высшего порядка (n-ого порядка)
24. Признаки возрастания и убывания функции
25. Экстремум функции. Признаки максимума и минимума функции.
26. Выпуклость графика функции. Точки перегиба.
27. Асимптоты графика функции.
28. Первообразная. Основное свойство первообразной.
29. Неопределенный интеграл и его геометрический смысл
30. Свойства неопределенного интеграла. Таблица интегралов
31. Метод непосредственного интегрирования
32. Метод замены переменной (метод подстановки).
33. Метод интегрирования по частям.
34. Определенный интеграл. Формула Ньютона-Лейбница. Геометрический смысл определенного интеграла. Криволинейная трапеция
35. Свойства определенного интеграла
36. Дифференциальное уравнение. Общее и частное решение ДУ. Задача Коши.
37. ДУ с разделяющимися переменными. ДУ второго порядка
38. Комбинаторика. Правило произведения, правило суммы в комбинаторике. Размещения. Сочетания. Перестановки.
39. Случайное событие. Виды случайных событий: равновозможные, совместные, зависимые, достоверные, невозможные.
40. Вероятность события.
41. Теоремы сложения вероятностей. Теоремы умножения вероятностей.
42. Формула полной вероятности. Формула Байеса.
43. Повторение испытаний. Формула Бернулли.
44. Случайная величина.
45. Дискретная и непрерывная случайная величина.
46. Закон распределения дискретной случайной величины.
47. Числовые характеристики дискретной случайной величины: мода, медиана, размах вариации, математическое ожидание, дисперсия, среднее квадратическое отклонение.
48. Биномиальный закон распределения ДСВ.
49. Статистическая информация. Математическая статистика.
50. Генеральная и выборочная совокупность. Объем выборки.
51. Таблицы распределения частот и относительных частот.
52. Точечные оценки параметров: выборочная средняя, выборочная дисперсия, выборочное среднее квадратическое отклонение.
53. Ошибки выборки.
54. Графическое представление данных: гистограмма, полигон, кумулята.
55. Комплексное число. Число, сопряженное и противоположное комплексному.
56. Графическое представление комплексного числа.
57. Модуль и аргумент комплексного числа.
58. Действия над комплексными числами.
59. Алгебраическая форма комплексного числа.
60. Тригонометрическая форма комплексного числа. Формула Муавра.
61. Показательная форма комплексного числа. Формулы Эйлера.
Приложение №1
Оформление титульного листа контрольной работы
| ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ БЛАГОВЕЩЕНСКИЙ МНОГОПРОФИЛЬНЫЙ ПРОФЕССИОНАЛЬНЫЙ КОЛЛЕДЖ Контрольная работа по математике студента группы ХТОз-1 ___________________________ (ФИО) Вариант ______ Дата сдачи на проверку __________ Дата проверки __________ Оценка __________ Преподаватель _____________ (подпись) г. Благовещенск, 2018г. |
Дата добавления: 2018-02-28; просмотров: 260; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
