Устойчивость одномерной динамической системы
ОБЩАЯ ТЕОРИЯ ДИНАМИЧЕСКИХ СИСТЕМ
Динамическая система
Динамическая система (ДС) – объект или процесс, состояние которого изменяется с течением времени.
Состояние механической системы – это координаты и скорости тел, входящих в систему.
Примеры динамических систем: физический маятник; электрический колебательный контур; генератор квазипериодических колебаний.
Если в ДС время  может изменяться непрерывно, то ДС называют системой с непрерывным временем, или потоком.
может изменяться непрерывно, то ДС называют системой с непрерывным временем, или потоком.
Если же в ДС  может изменяться лишь дискретно, то ДС называют системой с дискретным временем, или каскадом.
может изменяться лишь дискретно, то ДС называют системой с дискретным временем, или каскадом.
Вместо реальной ДС будем рассматривать её математическую модель.
Математическая модель динамической системы – это уравнение или система уравнений, описывающая изменение состояния ДС с течением времени.
Изменение состояния ДС во времени называют эволюцией ДС.
Эволюция одномерной динамической системы
Пусть состояние ДС характеризуется единственной величиной (координатой)  а эволюция задаётся дифференциальным уравнением (ДУ)
а эволюция задаётся дифференциальным уравнением (ДУ)
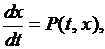
или
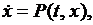 (2.1)
(2.1)
где точка над буквой означает производную по времени, а  – заданная функция, зависимая от неизвестной функции
– заданная функция, зависимая от неизвестной функции  Производная по времени имеет простой смысл:
Производная по времени имеет простой смысл: 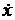 есть скорость изменения величины
есть скорость изменения величины  – состояния ДС. Если каким-нибудь способом мы найдём функцию
– состояния ДС. Если каким-нибудь способом мы найдём функцию  то будем знать, как изменяется состояние ДС с течением времени.
то будем знать, как изменяется состояние ДС с течением времени.
|
|
|
В процессе решения уравнения (2.1) приходится вычислять неопределённый интеграл, а поэтому всегда будет появляться произвольная постоянная величина. Обычно эту постоянную обозначают буквой 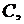 а решение любого уравнения вида (2.1) обозначают
а решение любого уравнения вида (2.1) обозначают 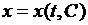 или
или 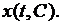
Решение, содержащее произвольную постоянную, называют общим решением.
Пример 1. Решив уравнение  вы получите
вы получите 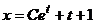 – общее решение (потому что содержит произвольную постоянную
– общее решение (потому что содержит произвольную постоянную  ).
).
Так как вместо  можно подставлять какие угодно числа, то выходит, что уравнение (2.1) имеет бесчисленное множество решений.
можно подставлять какие угодно числа, то выходит, что уравнение (2.1) имеет бесчисленное множество решений.
Если в общем решении вместо  вы подставите какое-нибудь число, получится частное решение.
вы подставите какое-нибудь число, получится частное решение.
(В примере 1 если вместо  подставить 9, получится
подставить 9, получится 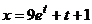 – частное решение).
– частное решение).
Теперь на плоскости 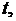
 вы сможете нарисовать график полученного частного решения.
вы сможете нарисовать график полученного частного решения.
График частного решения называют интегральной линией.
Вследствие того, что вместо  можно подставлять любые числа, общее решение
можно подставлять любые числа, общее решение 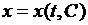 изобразится бесконечным количеством линий, и каждому значению
изобразится бесконечным количеством линий, и каждому значению  будет соответствовать своя линия. Эти линии заполнят собой некоторую область
будет соответствовать своя линия. Эти линии заполнят собой некоторую область 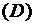 – область существования решений на плоскости
– область существования решений на плоскости 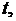
 Примеры интегральных линий, полученных в результате решения разных уравнений, и области
Примеры интегральных линий, полученных в результате решения разных уравнений, и области  где располагаются эти линии, показаны на рис. 2.1.
где располагаются эти линии, показаны на рис. 2.1.
|
|
|
В реальной практике обычно известно начальное состояние ДС: в начальный момент 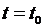 состояние ДС равно
состояние ДС равно 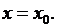
Требование того, что при 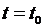 должно быть
должно быть 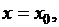 принято записывать в виде
принято записывать в виде 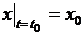 , или
, или 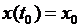 и называть начальным условием.
и называть начальным условием.
Пример 2. Если при 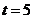 должно быть
должно быть  то это записывают в виде
то это записывают в виде 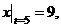 либо
либо 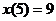 .
.
На плоскости 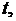
 начальное условие изображается точкой с координатами
начальное условие изображается точкой с координатами 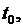
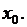 Эта точка, находясь в области
Эта точка, находясь в области  попадает на какую-то интегральную линию. Это означает, что наличие начального условия даёт возможность найти частное решение уравнения (2.1).
попадает на какую-то интегральную линию. Это означает, что наличие начального условия даёт возможность найти частное решение уравнения (2.1).
В общем случае возможно, что какие-то интегральные линии пересекаются между собой. Оказывается, что если функция 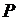 и её частная производная
и её частная производная 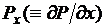 непрерывны в
непрерывны в  то интегральные линии не могут пересекаться. Иными словами, через каждую точку области
то интегральные линии не могут пересекаться. Иными словами, через каждую точку области 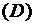 будет проходить ровно одна интегральная линия.
будет проходить ровно одна интегральная линия.
а б в
|
|
|
г д е
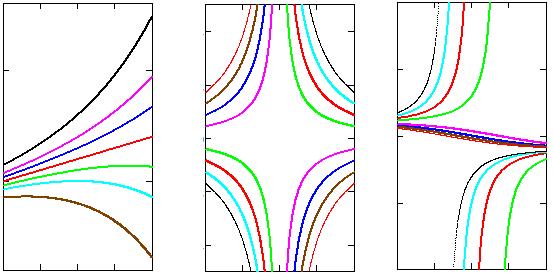
Рис. 2.1
Отметим, что на рис. 2.1 линии д и б схожи, хотя соответствуют разным уравнениям. Поэтому говорят, что эти семейства интегральных линий качественно эквивалентны.
Устойчивость одномерной динамической системы
Пусть эволюция ДС задаётся уравнением
 (3.1)
(3.1)
и начальным условием (входным данным)
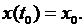 (3.2)
(3.2)
Решив задачу (3.1) – (3.2), получим частное решение
 (3.3)
(3.3)
В (3.3) правая часть 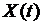 стала известной, поэтому выражение (3.3) отвечает на вопрос, как изменяется состояние ДС с течением времени.
стала известной, поэтому выражение (3.3) отвечает на вопрос, как изменяется состояние ДС с течением времени.
Обычно начальные данные не являются точными, так как получаются путём предыдущих измерений, а при измерении результат получается с некоторой погрешностью. А нам бы хотелось, чтобы неточность входных данных не сильно сказывалась на точности конечного ответа.
Решение называют устойчивым, если бесконечно малое изменение начальных данных приводит к бесконечно малому изменению решения на протяжении всего дальнейшего времени 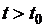 эволюции ДС.
эволюции ДС.
Эту идею выразим формулами, пригодными для исследования уравнений, описывающих ДС.
|
|
|
Дано: динамическая система описывается уравнением
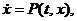 которое
которое 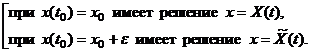
|
Решение  называется
устойчивым, если называется
устойчивым, если 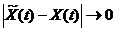 при при 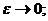 асимптотически устойчивым, если
асимптотически устойчивым, если 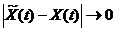 при при 
|
П р и м е ч а н и е. Задачу об устойчивости любого решения (3.3) всегда можно свести к задаче об устойчивости нулевого решения. Для этого достаточно от неизвестной функции  перейти к новой неизвестной
перейти к новой неизвестной  по формуле
по формуле 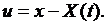 Естественно, уравнение для определения
Естественно, уравнение для определения  станет другим:
станет другим:  То, что это уравнение имеет нулевое решение
То, что это уравнение имеет нулевое решение  легко проверить подстановкой; будем иметь
легко проверить подстановкой; будем иметь  или
или  Получилось такое же равенство, как и (3.1), только неизвестная обозначена другой буквой. Поэтому во многих последующих задачах исследуется устойчивость только нулевого решения.
Получилось такое же равенство, как и (3.1), только неизвестная обозначена другой буквой. Поэтому во многих последующих задачах исследуется устойчивость только нулевого решения.
З а д а ч а 1. Решение дифференциального уравнения
 (а)
(а)
с начальным условием
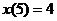
исследовать на устойчивость.
Запишем ДУ (а) в виде
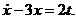 (б)
(б)
Это линейное уравнение, поэтому общее решение имеет вид 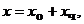 где
где 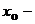 решение соответствующего однородного ДУ, а
решение соответствующего однородного ДУ, а 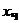 – частное решение. Отбросим в (б) правую часть и для полученного однородного ДУ
– частное решение. Отбросим в (б) правую часть и для полученного однородного ДУ 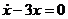 составим характеристическое уравнение
составим характеристическое уравнение 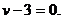 Оно имеет корень
Оно имеет корень 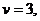 поэтому
поэтому  Теперь учтём правую часть. Правая часть в (б) подсказывает, что частное решение следует искать в подобном же виде:
Теперь учтём правую часть. Правая часть в (б) подсказывает, что частное решение следует искать в подобном же виде:  Тогда
Тогда  Подстановка
Подстановка 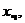
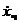 в (б) даёт
в (б) даёт  Раскроем скобки:
Раскроем скобки:  Составим систему уравнений
Составим систему уравнений
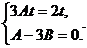
Отсюда находим 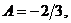
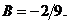 Следовательно,
Следовательно, 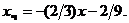 Общее решение уравнения (б) выглядит так:
Общее решение уравнения (б) выглядит так:
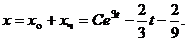
Запишем два одинаковых общих решения
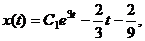 (в)
(в)
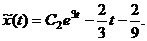 (г)
(г)
Для отыскания 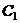 и
и  воспользуемся близкими друг другу начальными условиями
воспользуемся близкими друг другу начальными условиями

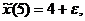 (д)
(д)
где 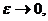 из-за чего будет выполняться условие
из-за чего будет выполняться условие 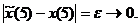 Подставим значения (д) в (в) и (г). Получим равенства
Подставим значения (д) в (в) и (г). Получим равенства
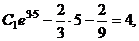

из которых находим 
 Подставим их в (в), (г). Получим частные решения
Подставим их в (в), (г). Получим частные решения
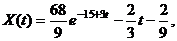 (д)
(д)
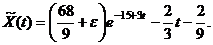
Тогда
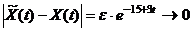 при
при 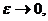
т.е. ДС устойчива. Однако если 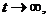 то
то 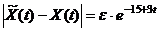 не стремится к нулю, а значит, ДС не является асимптотически устойчивой. ■
не стремится к нулю, а значит, ДС не является асимптотически устойчивой. ■
Дата добавления: 2018-02-28; просмотров: 366; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
