Шаг 1 – Пишем условие дифференцируемости
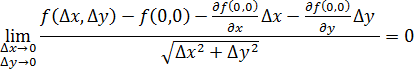
Шаг 2 – Вычисление частных производных
1. 
2. 
Шаг 2 – Вычисление предела
Пояснение:последнее равенство ( 
) возникает таким образом:
(при стремлении дельт к нулю), что верно в силу следующего неравенства:
Вывод: предел равен нулю, значит наша функция дифференцируема в нуле.
№3 – Разложить функцию 
в точке 
по формуле Тейлора до порядка 
включительно
Теория:
Практика:
Замечание:Сведения из теории нам особо не потребуются, так как разложение напрямую по формуле очень громоздко. Вместо этого нужно пользоваться готовыми разложениями в ряд некоторых функций.
Вот основные разложения вряд Маклорена: 
Задание:
, точка 
Шаг 1 – Ищем в fтакую подфункцию, которую мы могли бы разложить в ряд
В данном случае есть 
Шаг 2 – Приводим нашу функцию к удобному виду для разложения
Точка у нас , это значит, что просто так разложить в ряд Маклорена не удастся (так как там разложение происходит в нуле). Приведем к такому виду, чтобы можно было разложить (как бы) в нуле:
Теперь если x-1 заменить на u, у нас получится разложить в ряд Маклорена, в (u, y) = (0, 0) = (x-1, y), иначе говоря (u, y) = (0,0), при (x,y) = (1,0).
Пользуемся разложением экспоненты:
–это можно уже назвать ответом. Осталось только раскрыть скобки, что сделать рекомендуется.
№4 – Исследовать на экстремум функцию
Теория:
Практика:
Задание:
Шаг 1 – Ищем стационарные точки
Это такие точки, в которых частные производныеz равны нулю, то есть:
Решаем систему из двух уравнений и находим корни.
Учитывая, что знаменатель не равен нулю и логарифм берется от чисел больше нуля, у нас получаются следующие стационарные точки:
Шаг 2 – Смотрим чем являются стационарные точки. Точками минимума или максимума.
Для этого нужно вычислить второй дифференциал zв стационарных точках:
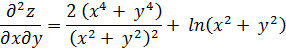
Итак, 
Теперь рассмотрим все точки. Подставим каждую из них в получившееся равенство:
в (1; 0) = 
У нас получилась квадратичная форма. Составим для нее матрицу:
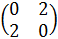, если все главные миноры положительны, то форма положительно определена, а значит в этой точке у функции точка минимума. Если же знак главных миноров чередуется, начиная с «-», то форма отрицательно определена иу функции в этой точке точка максимума.
Аналогично с другими точками.
№5 – Найти дифференциал в точке M функции заданной неявно
Практика:
Задание:
Создадим новую функцию уже от трех переменных 
Вычислим полный дифференциал :
Так как нужно вычислить дифференциал в точке M, то подставим её:
Так как нужно вычислить именно 
, товыразим его из формулы выше:
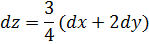
Это ответ.
№6 – Преобразовать уравнение, заменив независимые переменные
Практика:
Задание:
Шаг 1 – Получим uи v
Дата добавления: 2018-02-28; просмотров: 237; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!