КАТУШКА С МАГНИТОПРОВОДОМ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 17 страница

Подставив значение постоянной А в общее решение, найдем за­висимость тока от времени:

* = h + »св = 4»iSin(urf + г|;_м - ф) - I_msin(a|)_tt- ф)е"^^т,

где т =L/R —постоянная времени цепи.

Таким образом, во время переходного процесса ток в цепи состо­ит из синусоидальной составляющей и свободной составляющей, убывающей экспоненциально (рис. 5.11, б). Практически через ин­тервал времени Зт после замыкания ключа свободной составляю­щей можно пренебречь.

Если момент коммутации(t= 0) выбран так, что начальная фаза напряжения источника я|;_и = ф, то свободная составляющая тока рав­на нулю, т. е. переходного процесса нет и в цепи сразу устанавлива­ется синусоидальный ток.

Если начальная фаза напряжения источника = ф + тт/2, то интенсивность переходного процесса будет наибольшая. В момент времениt« Т/2 = тт/u; максимум тока будет наибольшим и в преде­ле при т > Т близким к 2I_m.

Аналогично рассчитывается переходный процесс при подключе­нии источника синусоидальной ЭДС к цепи с последовательно со­единенными резистивным и емкостным элементами и в других слу­чаях. И здесь переходный процесс зависит от начальной фазы на­пряжения источника: он отсутствует при = ф + тт/2, где ф = = arctg[—l/(wCR)]< 0, и выражен наиболее сильно при г|)_м = ф, ког­да максимальное напряжение на емкостном элементе может почти в 2 раза превысить амплитуду установившегося напряжения. Такое пе­ренапряжение может привести к пробою изоляции в высоковольт­ных установках.

5.9. Операторный метод расчета переходных процессов

Операторный метод не обладает физической наглядностью в силу своей глубокой математической формализации, но в ряде случаев упрощает расчеты. Его идея заключается в том, что расчет переход­ного процесса переносится из области функций действительной пе­ременной (времени t) в область функций комплексного переменно­го р, в которой дифференциальные уравнения преобразуются в ал­гебраические. Такое преобразование называется прямым. Получен­ное решение алгебраических уравнений обратным преобразовани­ем переносится в область действительного переменного. Строгое обоснование метода дается в курсе математики. Здесь познакомим­ся лишь с техникой применения операторного метода.

Для прямого преобразования функций времениf(t)применяет­ся преобразование Лапласа

оо

F(p)=fе-»<f(t)dt,                              (5.37)

О

что сокращенно записывается так:

F(p) = L[f(t)},

где функция времениf(t)— однозначная, называемая оригиналом, определенная приt> 0, интегрируемая в интервале времени 0 — оо и равная нулю приt < 0; F(p) — функция комплексного переменно­го р = а +juпри Reр = а > 0, называемая лапласовым изображе­нием.

Примем, что начало переходного процесса в цепи соответствует моменту времениt = 0.

В табл. 5.1 приведены примеры изображения простых функций. Отметим некоторые свойства преобразования Лапласа, называемые также теоремами.

1. Теорема о сложении или линейность преобразования

Ца_гт + а₂т] - аМАШ + а₂Щ(*)]. (5.38)

(5.39)

-Ир).

ff№

(5.40)

3. Теорема о дифференцировании h[df(t)/dt] = pF(p) - /(0+).

2. Теорема об интегрировании

Таблица5.1 Изображения функций по Лапласу Функция-оригинал /(£) Изображение функцииF(p) Выражение функции Вид функции i(0 = 0 приt < 0 1 приt^0 /< 1   1 Р   (единичная функция) 0 t e-at f\ 1   1 р + а 0 t   /-   а Р(Р + <*) 0 t t /- 1/ . 1 Р2 0 t     /-   (3 — а               s—^__________       0 1 t

 

4. Теорема запаздывания

L\f(t - Г)] = f(t)} = e~"^TF(p).                           (5.41)

Преобразование (5.37) позволяет получить соотношения между напряжениемu(t) ~ и и токомi(t) = г в операторной форме для резистивного, индуктивного и емкостного элементов.

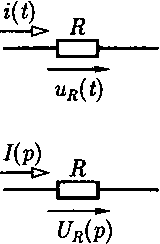
Изображение напряжения на резистивном элементеu_R(t) = Ri(t) по (5.25)

оо

U_R(p) = rJe~^pti(t)dt = Ri(p).                     (5.42)

о

Выражение (5.42) называется законом Ома в операторной фор­ме для резистивного элемента (рис. 5.12, а).

Изображение напряжения u_L— L— на индуктивном элементе по (5.38) и (5.40)       ^dt

U_L(p) = -ЬЦр) + рЬЦр),                       (5.43)

где г(0) = г(0_) = г(0+) — ток в индуктивном элементе в момент коммутацииt= 0, учитывающий начальные условия (5.1).

Напряжение на емкостном элементе, начиная с момента времени t= 0 возникновения переходного процесса в общем случае,

Г

u_c{t) =_%(0) • 1 (t) + i(t)dt,

о

где г/с(0) ^{= и}с(0-) =              ~~ напряжение на емкостном элементе,

соответствующее начальному условию (5.2).

Учитывая изображение единичной функцииL[l(t)] = 1/р (см. табл.5.1) и соотношения (5.38) и (5.39), найдем изображение напря­женияu_c(t):

и_с(р) = ^ + ±1(р).                                 (5.44)

Выражениям (5.43) и (5.44) соответствуют схемы замещения ин­дуктивного и емкостного элементов в операторной форме на рис. 5.12, бив.

форме для индуктивного элемента UL(p) = рЬЦр); для емкостного элемента ис(р) =j^m

Если начальные условия нулевые, т. е. ?₇ (0 ) = 0 и '%(0_) = 0, то выражения (5.43) и (5.44) примут вид закона Ома в операторной

(5.45а)

(5.456)

i(t)

»(<) С =^41---- Uc(t) J_ МО) 1(р) рС р =41-0- Uc(t) в

uL{t) pL -MO) m) б

гдеpLи 1/(рС) — сопротивления индуктивного и емкостного эле­ментов в операторной форме.

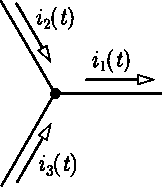
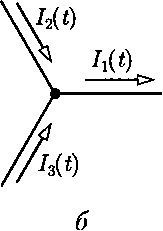
Воспользовавшись линейностью преобразования Лапласа (5.38)

п

для суммы токов в любом узле цепи          — 0> получим первый

к=1

закон Кирхгофа в операторной форме:

= 0,                              (5.46)

к = 1

гдеI_k(p) =L[i_k(t)](рис. 5.13, а, б).

Аналогично и второму закону Кирхгофа для любого контура по (2.29)

тп

= о,

к=1

или в другой форме по (2.49)

£«*(<) =

к=1

соответствует его представление в операторной форме

т

J2u_k(t) = о,                                (5.47а)

к=1

Или

п           т

=                                     (5.476)

где = Ь[и*(«)] и ад = L[e*(t)]-

При расчете переходного процесса операторным методом полез­но выделить несколько логически самостоятельных этапов:

1) представить исходные данные о параметрах всех элементов схемы цепи в операторной форме. Это оз­начает, что, во-первых, ЭДС источ­ников напряжения и токи источни­ков тока, заданные мгновенными значениямиe(t)иJ{t),следует пред­ставить по (5.37) соответствующи­ми изображениями Е(р) иJ(p)и, во- вторых, пассивные элементы — схе­мами замещения по рис. 5.12;                                  Рис. 5.13

2) для полученной схемы замещения в операторной форме со­ставить и решить полную систему независимых уравнений по пер­вому [см. (5.46)] и второму [см. (5.47)] законам Кирхгофа в опера­торной форме, т.е. найти изображениеF(p)искомой величины, на­пример ток 1(р);

(5.48)

3) наиболее часто изображение имеет вид рациональной дроби F(p) =^^у Для которой обратным преобразованием нужно най­ти оригиналf(t), например токi(t).Для этого можно воспользовать­ся теоремой разложения

fit) ₌ у ^N(Pt)_еп>.

гдеN(p) и М(р) — многочлены в числителе и знаменателе изображе­нияF(p); М'(р) — производная многочлена М(р) по р; р_к — корни многочлена М(р) = 0, где предполагается, что корни простые. Если получаются кратные корни, то теорема разложения записывается в другой форме.

В качестве примера рассчитаем ток в цепи, содержащий В = 3 ветви и У = 2 узла (рис. 5.14, а) при ЭДСe(t)= Ее~^ы (рис. 5.14, б) и нулевых начальных условиях, т.е. при г_ь(0_) = 0, операторным ме­тодом.

Для этого выполним последовательно все этапы расчета:

1) по правилам, показанным на рис. 5.12, составим схему замеще­ния в операторной форме (рис. 5.14, в), где Е(р) = Е/(р + а) — изоб­ражение функции ЭДСe(t),найденное по (5.37) или выписанное из табл. 5.1;

(5.49а)

(5.496) (5.49в)

2) при выбранных положительных направлениях токов составим одно (У—1 = 2 — 1 = 1) уравнение по первому закону Кирхгофа для узла а:

-hip) +Up) + Up) = о

и два (К = В — У + 1 = 3 — 2 + 1 = 2) уравнения по второму закону Кирхгофа для контуров 1 и 2:

ад + ОД = ад; ад - ад = о

или

ДОД+ pU_L(p) = Е{р); ДОД - pLI_L(p) = О,

Щ

PI

R-.

ч

u2

S,

e(t)

©

b a a

Ri

h(p)

иы i pl\

E(p)

uM I * 2Л.

Л) ад

© !

R.

b в

Рис. 5.14

где учтены законы Ома для пассивных элементов (2.42) и (2.45а). Решив систему трех алгебраических уравнений (5.49), определим ток в операторной форме:

R₂E

Щр) М(р)

(р + а)

L(RI + R₂)

Многочлен М(р) = 0 имеет два корня: _Pl= -а и р₂ =

L(R_X+R₂)

L(Ri + Яг)

h(p)

R1R2

Р +

-RXR2

= -(3, aМ\р) = 2р + а + (3. По теореме разложения (5.48) опреде­лим ток:

-pr

[e

-at

4(t) =

ERn

R_xR₂- aL{Ri + R₂)

изменение тока показано на рис. 5.14, б.

Во многих практических случаях расчетов пользоваться прямым [см. (5.37)] и обратным [см. (5.48)] преобразованиями нет необходи­мости, так как имеются обширные справочные материалы соответствия оригиналов и их изображений, подобные приведенным в табл. 5.1.

5.10. Расчет переходных процессов на ЭВМ

Токиi_Lв индуктивных и напряжения и_сна емкостных элементах определяют энергию этих элементов [см. (2.5) и (2.13)], инерцион­ность изменения которой при различного рода коммутациях вызы­вает переходный процесс в цепи. Совокупность токовi_Lи напряже­ний и_с называется переменными состояния цепи.

Различают два подхода при применении ЭВМ для расчета цепи. Первый подход предполагает универсальные программные средства, включая входной язык формирования системы уравнений цепи по ее топологии. Такие средства созданы в настоящее время, но их раз­работка и совершенствование требуют специальных знаний в обла­сти математики и программирования. Второй подход, рассмотрен­ный в книге, основан на численном решении систем уравнений цепи с помощью подпрограмм стандартного математического обеспече­ния ЭВМ. При этом расчетчик самостоятельно составляет систему уравнений в форме, необходимой для реализации подпрограмм. Для расчета стационарных режимов цепи это — система уравнений в мат­ричной форме [см. (1.10)], а для расчета переходных процессов — система дифференциальных уравнений первого порядка относитель­но переменных состояния.

В последнем случае система уравнений на основе законов Кирх­гофа, Ома, электромагнитной индукции (2.3) и соотношения между током и напряжением для емкостных элементов (2.11), описываю­щая переходный процесс в цепи, преобразуется в систему уравне­ний, разрешенную относительно первых производных токовi_Lи на­пряжений и_с:

di_Ll/dt =f₁(i_LV---,i_Lmi--'>>'u>_cv...,u_Cn,t)]

dhm/dt —fm(hv-'>hm^"^,>^ucv"">^ucn^)^ du_ci/dt =

^^иСт! ^ — fm+n(hv">hm^--'>^UCV">^UCn^)\

где тип — число индуктивных и емкостных элементов с начальны­ми значениями токов s_L1(0),...,i_Lm(0) и напряжений г/_С1(0),...,u_Cn(0).

Система уравнений (5.37) называется системой уравнений в нор­мальной форме. Для ее решения разработан ряд эффективных чис­ленных методов: метод Эйлера, метод Рунге — Кутта и др., входящих в современное стандартное математическое обеспечение ЭВМ.

Например, система уравнений, описывающая переходный про­цесс в цепи на рис. 5.15 и составленная на основе законов Кирхгофа

С ic

Ф)

0

R

-ic+ к + Ч = 0; и_с + u_L= e(f); и_с ~ Щ = 0 или с зачетом (2.3) и (2.11)

Рис. 5.15

_тdir             / ч

= о.

fi(uc,t);

«<■ + = Ф);

после исключения тока г_д преобразуется в систему уравнений в нор­мальной форме относительно переменных состоянияi_Lи и_с:

^ _Ш - Ц_С) _

dt        L

du_c_ i_L(e(t)-u_c)_ ₍. dt ~C⁺ RC

гдеe(t) — ЭДС, возбуждающая переходный процесс в цепи при за­данных начальных условиях и_с(0) и i_L(0).

---

Дата добавления: 2018-02-28; просмотров: 297; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

⇐ Предыдущая12131415161718192021Следующая ⇒

---

Мы поможем в написании ваших работ!