V241П Электромагнитная индукция. Закон Фарадея. Тема: 060 Механические колебания и волны
Дисциплина: Физика
Тема: 060 Механические колебания и волны
V061 – П Механические колебания
S061 – П Механические колебания (незатухающие, затухающие, вынужденные 30 заданий)
1. [Уд1] (ВО1) Полная механическая энергия пружинного маятника увеличилась в 2 раза. При этом амплитуда колебаний … раз(а).
1) увеличилась в 2
2) увеличилась в 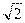
3) уменьшилась в 2
4) уменьшилась в 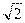
:2
2. [Уд1] (ВО1) Материальная точка совершает гармонические колебания по закону  . График, на котором изображена зависимость проекции ускорения
. График, на котором изображена зависимость проекции ускорения 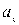 этой точки от времени t –
этой точки от времени t –
1) 1 
2) 2
3) 3
4) 4
:1
3. [Уд1] (ВО1) Материальная точка совершает колебания по закону 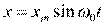 . График, на котором изображена зависимость кинетической энергии материальной точки от времени –
. График, на котором изображена зависимость кинетической энергии материальной точки от времени –

1) 1
2) 2
3) 3
4) 4
:2
4. [Уд1] (ВО1) Материальная точка совершает колебания по закону  . График, на котором изображена зависимость потенциальной энергии материальной точки от времени –
. График, на котором изображена зависимость потенциальной энергии материальной точки от времени –

1) 1
2) 2
3) 3
4) 4
:4
5. [Уд1] (ВО1) На рисунке представлены графики гармонических колебаний материальных точек одинаковой массы, А1=2А2. Соотношение амплитудных значений ускорений колеблющихся точек следующее 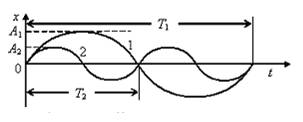
1) am1 = am2
2) a m1 < am2
3) a m1 > am2
4) Однозначного ответа нет
:2
6. [Уд1] (ВО1) На рисунке представлены графики гармонических колебаний материальных точек одинаковой массы, А1=2А2. Соотношение амплитудных значений скоростей колеблющихся точек следующее 
|
|
|
1) V m1 = Vm2
2) V m1 < Vm2
3) V m1 > Vm2
4) Однозначного ответа нет
:1
7. [Уд1] (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми коэффициентами упругости k. Маятник, имеющий наибольшую массу – … кг.
1) 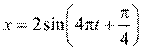
2) 
3) 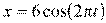
4) 
:4
8. [Уд1] (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми коэффициентами упругости k. Маятник, имеющий наименьшую массу – … кг.
1) 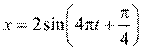
2) 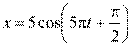
3) 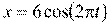
4) 
:2
9. [Уд1] (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми массами. Маятник, имеющий наибольший коэффициент упругости k – … Н/м.
1) 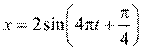
2) 
3) 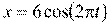
4) 
:2
10. [Уд1] (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми массами. Маятник, имеющий наименьший коэффициент упругости k – … Н/м.
1) 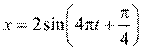
2) 
3) 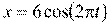
4) 
:4
11. [Уд1] (ВО1) Даны уравнения гармонических колебаний материальной точки массы m . Коэффициент упругости k наибольший в случае
1) х = 3 sin (2πt + π) м
2) х = 3 cos (4πt + 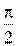 ) м
) м
3) x = 5 cos (15πt – 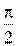 ) м
) м
4) x = 5 sin (5πt) м
:3
12. [Уд1] (ВО1) На рис.1 изображена зависимость проекции скорости материальной точки, совершающей гармонические колебания, от времени. На рис.2 график зависимости от времени проекции ускорения этой точки изображен под номером 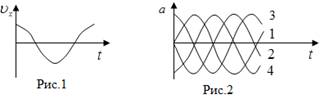
|
|
|
1) 1
2) 2
3) 3
4) 4
:2
13. [Уд1] (ВО1) На рис.1 изображена зависимость проекции скорости материальной точки, совершающей гармонические колебания, от времени. На рис.2 график зависимости от времени смещения от положения равновесия этой точки изображен под номером 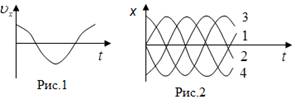
1) 1
2) 2
3) 3
4) 4
:1
14. [Уд1] (ВО1) Материальная точка массой m = 0,1 кг колеблется так, что проекция ах ускорения зависит от времени в соответствии с уравнением ах = 10 sin 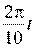 , м/с2. Проекция силы на ось ОХ, действующей на материальную точку в момент времени t =
, м/с2. Проекция силы на ось ОХ, действующей на материальную точку в момент времени t = 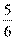 c равна … Н.
c равна … Н.
1) 0,25
2) 0,5
3) 0,83
4) 1,0
: 2
15. [Уд1] (ВО1) Если в колебательной системе изменяющаяся физическая величина описывается законом 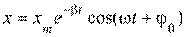 , то частота затухающих колебаний связана с собственной частотой соотношением
, то частота затухающих колебаний связана с собственной частотой соотношением
1) 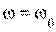
2) 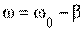
3) 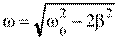
4) 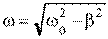
:4
16. [Уд1] (ВО1) Уравнение затухающих колебаний материальной точки имеет вид  , где ω = 6 рад/с, β = 8 с-1. Логарифмический декремент затухания колебаний равен
, где ω = 6 рад/с, β = 8 с-1. Логарифмический декремент затухания колебаний равен
1) 83,7
2) 8,37
3) 0,63
4) 62,8
:2
17. [Уд1] (ВО1) Уравнение затухающих колебаний материальной точки имеет вид  , где ω = 6 рад/с, логарифмический декремент затухания λ = 8,37 . Коэффициент затухания колебаний равен … с-1.
, где ω = 6 рад/с, логарифмический декремент затухания λ = 8,37 . Коэффициент затухания колебаний равен … с-1.
|
|
|
1) 8,0
2) 1,3
3) 0,6
4) 3,0
:1
18. [Уд1] (ВО1) Уравнение затухающих колебаний материальной точки имеет вид 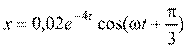 ,м. Если логарифмический декремент затухания колебаний λ = 0,1, то период T затухающих колебаний равен … мс.
,м. Если логарифмический декремент затухания колебаний λ = 0,1, то период T затухающих колебаний равен … мс.
1) 20
2) 25
3) 40
4) 75
:2
19. [Уд1] (ВО1) Уравнение затухающих колебаний материальной точки имеет вид 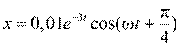 ,м. Если логарифмический декремент затухания колебаний λ = 0,02, то частота ω затухающих колебаний равна … рад/с.
,м. Если логарифмический декремент затухания колебаний λ = 0,02, то частота ω затухающих колебаний равна … рад/с.
1) 50π
2) 100π
3) 200π
4) 300π
:4
20. [Уд1] (ВО1) На рисунке изображен график затухающих колебаний, где х - колеблющаяся величина, описываемая уравнением х(t) = A0e-βt sin (ωt + φ). Коэффициент затухания β равен 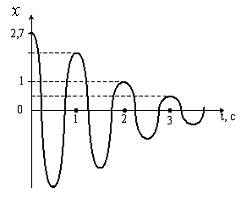
1) 0,5
2) 1
3) 2
4) 2,7
:1
21. [Уд1] (ВО1) Приведены графики механических колебаний. Два графика соответствуют зависимости смещения х, два других – зависимости кинетической Wk и полной энергии W системы от времени. Обозначения вертикальных осей не указаны.

Зависимости кинетической энергии системы от времени в неконсервативной системе соответствует график
1) 1
2) 2
3) 3
4) 4
:2
22. [Уд1] (ВО1) Приведены графики механических колебаний. Два графика соответствуют зависимости смещения х, два других – зависимости кинетической Wk и полной энергии W системы от времени. Обозначения вертикальных осей не указаны.
|
|
|

Зависимости полной энергии W системы от времени в консервативной системе соответствует график
1) 1
2) 2
3) 3
4) 4
:1
23. [Уд1] (ВО1) Приведены графики механических колебаний. Два графика соответствуют зависимости смещения х, два других – зависимости кинетической Wk и полной энергии W системы от времени. Обозначения вертикальных осей не указаны.

Зависимости смещения х от времени в консервативной системе соответствует график
1) 1
2) 2
3) 3
4) 4
:4
24. [Уд1] (ВО1) Приведены графики механических колебаний. Два графика соответствуют зависимости смещения х, два других – зависимости кинетической Wk и полной энергии W системы от времени. Обозначения вертикальных осей не указаны.
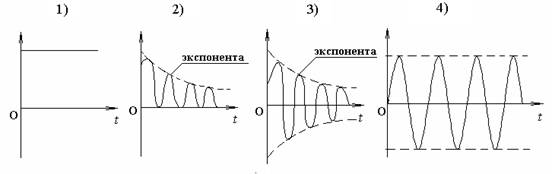
Зависимости смещения х от времени в неконсервативной системе соответствует график
1) 1
2) 2
3) 3
4) 4
:3
25. [Уд1] (ВО1) Приведены графики зависимости кинетической Wк и полной механической W энергии от времени t при различных видах механических колебаний. Обозначения осей ординат не указаны.
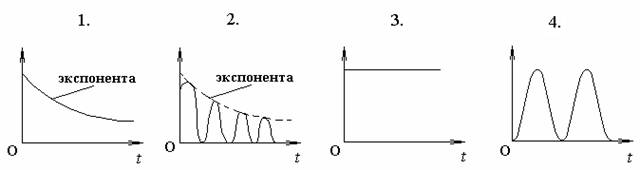
Зависимость полной энергии W от времени описывается … графиками.
1) 1 и 2
2) 2 и 4
3) 3 и 1
4) 4 и 3
:3
26. [Уд1] (ВО1) Уравнение движения пружинного маятника 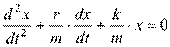 является дифференциальным уравнением … колебаний.
является дифференциальным уравнением … колебаний.
1) свободных незатухающих
2) затухающих
3) вынужденных
4) апериодических
:2
27. [Уд1] (ВО1) Уравнение движения пружинного маятника  является дифференциальным уравнением … колебаний.
является дифференциальным уравнением … колебаний.
1) свободных незатухающих
2) затухающих
3) вынужденных
4) апериодических
:1
28. [Уд1] (ВО1) Уравнение движения пружинного маятника 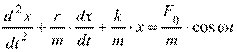 является дифференциальным уравнением … колебаний.
является дифференциальным уравнением … колебаний.
1) свободных незатухающих
2) затухающих
3) вынужденных
4) апериодических
:3
29. [Уд1] (ВО1) Решение дифференциального уравнения  движения пружинного маятника ищется в виде зависимости
движения пружинного маятника ищется в виде зависимости
1) х = Acos (ω0t +ϕo)
2) х = Ao e-βt cos (ωt +ϕo)
3) x = 2A cos 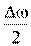 t ⋅cosωt
t ⋅cosωt
4) х = Ao e-2βt cos (ω0t +ϕo)
:2
30. [Уд1] (ВО1) На рисунке представлена зависимость амплитуды колебаний груза на пружине с жесткостью k = 10 Н/м от частоты внешней силы. Максимальная энергия в этой системе равна … Дж. 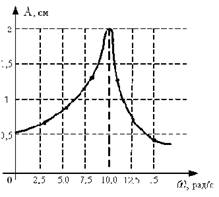
1) 0,002
2) 0,004
3) 20
4) 40
:1
C061 – П Механические колебания (сложение колебаний) – 16 заданий
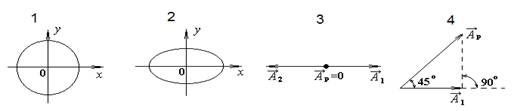
1. [Уд1] (ВОМ) На рисунке под номерами 1, 2 изображены траектории результирующего движения при сложении двух взаимно перпендикулярных гармонических колебаний, а под номерами 3, 4 – векторные диаграммы сложения гармонических колебаний одного направления и одинаковой частоты ( 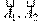 - векторы амплитуд складываемых колебаний,
- векторы амплитуд складываемых колебаний, 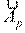 - вектор амплитуды результирующего колебания). Амплитуды складываемых колебаний равны для случаев, приведенных под номерами
- вектор амплитуды результирующего колебания). Амплитуды складываемых колебаний равны для случаев, приведенных под номерами
 |
:1,3,4
2. [Уд1] (ВО1) Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями x = 3cosωt и y = -6cosωt. Траекторией результирующего движения точки является
1) прямая линия
2) парабола
3) окружность
4) эллипс
:1
3. [Уд1] (ВО1) Складываются два гармонических колебания, происходящих в одном направлении.
1) 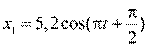 ,м и
,м и 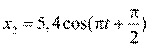 , м.
, м.
2) 
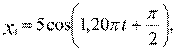 м и
м и 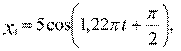 м.
м.
3) 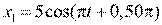 , м и
, м и 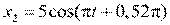 , м.
, м.
4) 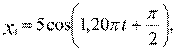 м и
м и 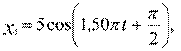 м.
м.
Результирующее движение называется биением в (во) … случае.
1) 1
2) 2
3) 3
4) 4
:2
4. [Уд1] (ВО1) Складываются два гармонических колебания, происходящих в одном направлении: 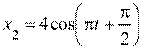 см и
см и 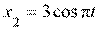 см. Амплитуда результирующего движения равна … см.
см. Амплитуда результирующего движения равна … см.
1) 7
2) 5
3) 3,5
4) 1
:2
5. [Уд1] (ВО1) Результат сложения двух гармонических колебаний одного направления с одинаковыми амплитудами и близкими частотами описывает уравнение
1) х = Acos (ω0t +ϕo)
2) A2 = A12 +A22 + 2A1A2 cos Δϕ
3) x = 2A cos 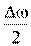 t ⋅cosωt
t ⋅cosωt
4) 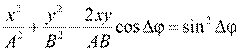
:3
6. [Уд1] (ВО1) Уравнение траектории при сложении двух гармонических колебаний взаимно перпендикулярных направлений с отличающимися амплитудами и одинаковыми частотами –
1) х = Acos (ω0t +ϕo)
2) A2 = A12 +A22 + 2A1A2 cos Δϕ
3) x = 2A cos 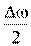 t ⋅cosωt
t ⋅cosωt
4) 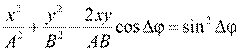
:4
7. [Уд1] (ВО1) Точка М одновременно совершает колебания по гармоническому закону вдоль осей координат ОХ и ОУ с одинаковыми амплитудами, разность фаз равна 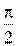 . При соотношении частот 1:1 траектория точки имеет вид, соответствующий схеме под номером
. При соотношении частот 1:1 траектория точки имеет вид, соответствующий схеме под номером
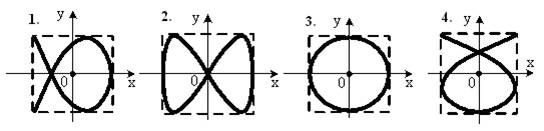
1) 1
2) 2
3) 3
4) 4
:3
8. [Уд1] (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с различными амплитудами, но одинаковыми частотами. При разности фаз π траектория точки имеет вид, соответствующий схеме под номером
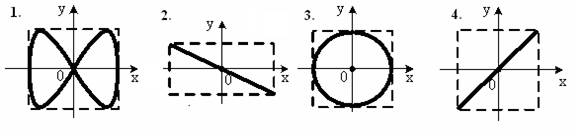
1) 1
2) 2
3) 3
4) 4
:2
9. [Уд1] (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с одинаковыми амплитудами, и одинаковыми частотами. При разности фаз 0 траектория точки имеет вид, соответствующий схеме под номером

1) 1
2) 2
3) 3
4) 4
:4
10. [Уд1] (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с одинаковыми амплитудами, но разными частотами. При разности фаз π/2 траектория точки имеет вид, соответствующий схеме под номером

1) 1
2) 2
3) 3
4) 4
:1
11. [Уд1] (ВО1) Точка М одновременно колеблется по гармоническому закону вдоль оcей координат ОХ и ОУ с одинаковыми амплитудами, разность фаз равна 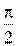 . При соотношении частот 3:2 траектория точки имеет вид на схеме, обозначенной номером
. При соотношении частот 3:2 траектория точки имеет вид на схеме, обозначенной номером
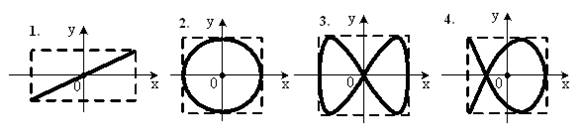
1) 1
2) 2
3) 3
4) 4
:4
12. [Уд1] (ВО1) При сложении двух взаимно-перпендикулярных колебаний одинаковой частоты траектория результирующего движения материальной точки представлена на рисунке. Тогда разность фаз Δϕ складываемых колебаний равна 
1) π
2) 0
3) 3π
4) π/2
:2
13. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1=4 см и А2=3 см. Амплитуда их результирующего колебания Ар=7 см. Разность фаз складываемых колебаний равна
1) ∆φ = 0
2) ∆φ = 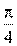
3) ∆φ = 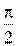
4) ∆φ = π
:1
14. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Амплитуда их результирующего колебания Ар = 5 см. Разность фаз складываемых колебаний равна
1) ∆φ = 0
2) ∆φ = 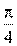
3) ∆φ = 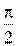
4) ∆φ = π
:3
15. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Амплитуда их результирующего колебания Ар = 1 см. Разность фаз складываемых колебаний равна
1) ∆φ = 0
2) ∆φ = 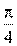
3) ∆φ = 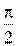
4) ∆φ = π
:4
16. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Разность фаз складываемых колебаний равна ∆φ = 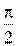 . Амплитуда их результирующего колебания составляет … см.
. Амплитуда их результирующего колебания составляет … см.
1) 7
2) 5
3) 1
4) 12
:2
Дисциплина: Физика
Тема: 060 Механические колебания и волны
V064 – П Волновое движение
S064 – П Волновое движение - 10 заданий
1. [Уд1] (ВО1) Решением волнового уравнения 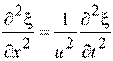 является уравнение плоской монохроматической волны ξ, которая распространяется вдоль направления оси Ох. Это уравнение представлено формулой
является уравнение плоской монохроматической волны ξ, которая распространяется вдоль направления оси Ох. Это уравнение представлено формулой
1) 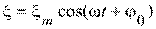
2) 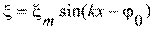
3) 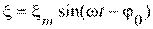
4) 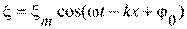
:4
2. [Уд1] (ВО1) Уравнение плоской синусоидальной волны, распространяющейся вдоль оси Ох со скоростью v = 500 м/с, имеет вид ξ = 0,01 sin (ωt – 2х). Циклическая частота ω равна … рад·с-1.
1) 1000
2) 159
3) 0,02
4) 0,001
:1
3. [Уд1] (ВО1) Уравнение плоской монохроматической волны ξ, которая распространяется вдоль положительного направления оси Ох представлено формулой
1) 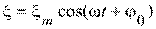
2) 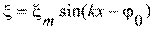
3) 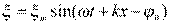
4) 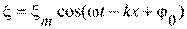
:4
4. [Уд1] (ВО1) Уравнение сферической монохроматической волны ξ представлено формулой
1) 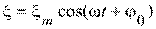
2) 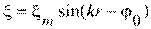
3) 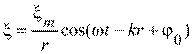
4) 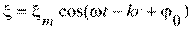
:3
5. [Уд1] (ВО1) Уравнение стоячей волны ξ представлено формулой
1) 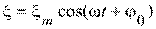
2) 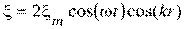
3) 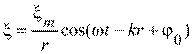
4) 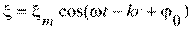
:2
6. [Уд1] (ВО1) При интерференции двух волн результирующая волна характеризуется изменением
1) частоты волны
2) длины волны
3) распределения энергии в пространстве
4) периода колебаний
:3
7. [Уд1] (ВО1) Источник колебаний, находится в упругой среде, и точки этой среды находятся на расстоянии 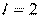 м от источника. Частота колебаний
м от источника. Частота колебаний 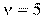 Гц, фазовая скорость волны
Гц, фазовая скорость волны 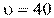 м/с. Разность фаз
м/с. Разность фаз 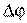 равна … рад.
равна … рад.
1) 2π
2) 0,5π
3) 0,25π
4) 0,33π
:2
8. [Уд1] (ВО1) Если разность фаз колебаний источника волн в упругой среде равна 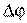 = 0,5π рад, и точки этой среды находятся на расстоянии
= 0,5π рад, и точки этой среды находятся на расстоянии 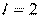 м от источника. Частота колебаний составляет
м от источника. Частота колебаний составляет 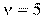 Гц, тогда фазовая скорость волны равна … м/с.
Гц, тогда фазовая скорость волны равна … м/с.
1) 20
2) 30
3) 40
4) 50
:3
9. [Уд1] (О) Точки пространства, в которых амплитуда колебаний стоячей волны, равна нулю, называются … стоячей волны.
Узлы, узлами
10. [Уд1] (ВО1) В стоячей волне расстояния между двумя соседними пучностями равно
1) λ
2) λ/2
3) 3λ/2
4) 2λ
:2
C064 – П Волновое движение (графики) – 4 задания
1. [Уд1] (ВО1) В упругой среде в положительном направлении оси 0x распространяется плоская волна. На рисунке приведен график зависимости смещения ξ частицы среды от времени t в произвольной точке оси 0х. Циклическая частота волны … рад/c. 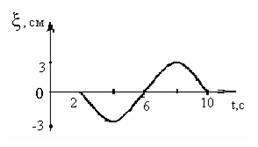
1) 2π
2) 0,8π
3) π/4
4) π/3
:3
2. [Уд1] (ВО1) В упругой среде в положительном направлении оси 0x распространяется плоская волна. На рисунке приведен график зависимости смещения ξ частицы среды от времени t в произвольной точке оси 0х. Если длина волны равна 40 м, то скорость распространения составляет … м/c. 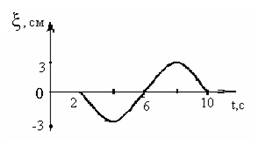
1) 2
2) 5
3) 8
4) 10
:2
3. [Уд1] (ВО1) На рисунке приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 6 с. Источник колебаний находится в точке с координатой х = 0. В начальный момент времени (t = 0) все частицы среды находились в покое. Фазовая скорость волны равна … м/c. 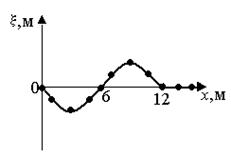
1) 12
2) 6
3) 4
4) 2
:4
4. [Уд1] (ВО1) На рисунке приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 6 с. Источник колебаний находится в точке с координатой х = 0. В начальный момент времени (t = 0) все частицы среды находились в покое. Циклическая частота волны равна … рад/c. 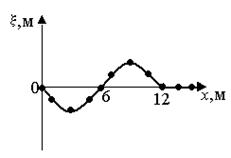
1) 2π
2) 0,8π
3) π/4
4) π/3
:4
Дисциплина: Физика
Тема: 240 Электромагнитная индукция
v241П Электромагнитная индукция. Закон Фарадея
Дата добавления: 2018-02-28; просмотров: 574; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
