Разложение функций в степенные ряды.
Возможны различные способы разложения функции в степенной ряд:
1) разложение при помощи рядов Тейлора и Маклорена
2) разложения в степенной ряд при помощи алгебраического деления.
Этот способ пригоден для разложения в ряд алгебраических дробей.
3) разложения функции в ряд при помощи интегрирования.


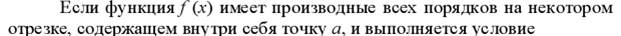

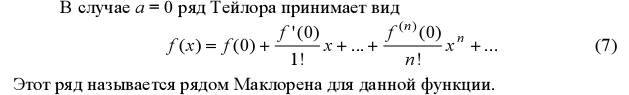

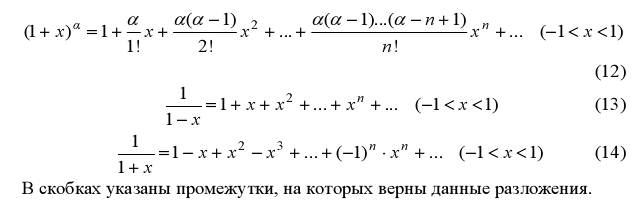

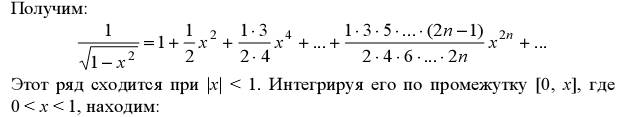
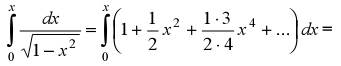
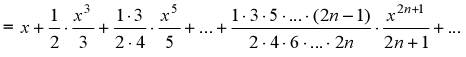
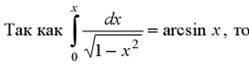
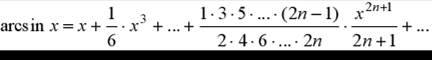

Пример 2. Разложить в ряд функцию 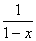 .
.
Решение. Применим к функции формулу Маклорена:
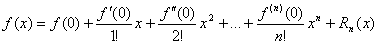 ,
,
получаем: 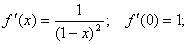
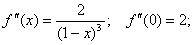
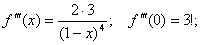
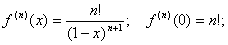 Итого, получаем:
Итого, получаем: 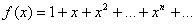
С помощью интегрирования можно разлагать в ряд такую функцию, для которой известно или может быть легко найдено разложение в ряд ее производной.
Находим дифференциал функции  и интегрируем его в пределах от 0 до х.
и интегрируем его в пределах от 0 до х.
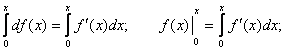
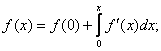
Пример 3. Разложить в ряд функцию 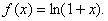
Решение. Решим эту задачу при помощи интегрирования.
При 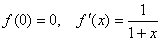 получаем по приведенной выше формуле:
получаем по приведенной выше формуле: 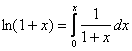
Разложение в ряд функции 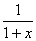 имеет вид:
имеет вид: 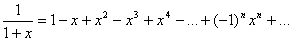
Тогда получаем: 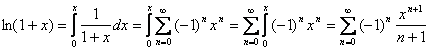
Окончательно получим: 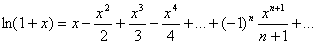
Пример 4. Разложить в степенной ряд функцию  .
.
Решение. Применим разложение в ряд с помощью интегрирования.
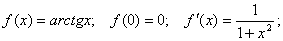

Подынтегральная функция может быть разложена в ряд методом алгебраического деления:
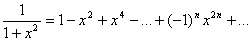
Тогда 
Окончательно получаем: 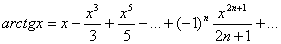
Замечание: В простейших разложениях вроде 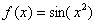 ,
,  или
или  в нужные табличные разложения вместо α необходимо подставить
в нужные табличные разложения вместо α необходимо подставить 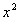 ,
,  ,
, 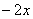 и упростить полученные ряды.
и упростить полученные ряды.
Пример 5. Разложить функцию 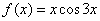 в ряд Маклорена. Найти область сходимости полученного ряда.
в ряд Маклорена. Найти область сходимости полученного ряда.
|
|
|
Решение. Используем элементарное разложение: 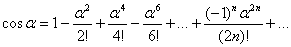 .
.
Область сходимости ряда: 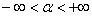
В данном случае  . Тогда
. Тогда 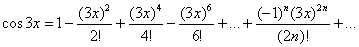
В числителях раскрываем скобки: 
Теперь умножаем обе части на х: 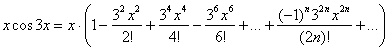
В итоге искомое разложение функции в ряд: 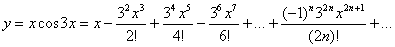
Область сходимости: Разложение косинуса сходится при ЛЮБОМ значении α: 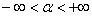 , а значит и при
, а значит и при  . Домножение
. Домножение  на х не играет никакой роли в плане сходимости. Поэтому область сходимости полученного ряда:
на х не играет никакой роли в плане сходимости. Поэтому область сходимости полученного ряда: 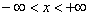
Пример 6. Разложить функцию 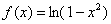 в ряд по степеням
в ряд по степеням 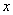 . Найти область сходимости ряда.
. Найти область сходимости ряда.
Решение. В таблице находим похожее разложение: 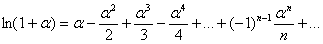
Область сходимости ряда: 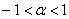 , концы интервала нужно исследовать дополнительно.
, концы интервала нужно исследовать дополнительно.
Перепишем функцию немного по-другому: 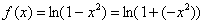
Таким образом, 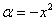 и:
и: 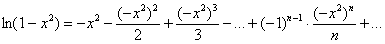
Окончательно: 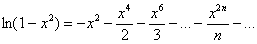
Теперь нужно определить область сходимости. Смотрим на табличное неравенство 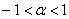 . В нашем случае функция разложилась в ряд
. В нашем случае функция разложилась в ряд 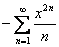 . Используя признак Даламбера, легко найти интервал сходимости ряда:
. Используя признак Даламбера, легко найти интервал сходимости ряда: 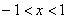 .
.
Исследуем на концах интервала: Если подставить значения 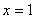 ,
, 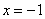 , то в обоих случаях получится расходящийся гармонический ряд
, то в обоих случаях получится расходящийся гармонический ряд 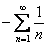 (знак перед рядом не влияет на сходимость).
(знак перед рядом не влияет на сходимость).
Таким образом, область сходимости полученного ряда: 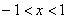
Пример 7. Разложить функцию 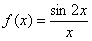 в ряд по степеням
в ряд по степеням 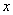 . Найти область сходимости ряда.
. Найти область сходимости ряда.
Решение. Используем разложение: 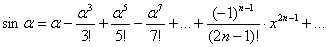 .
.
|
|
|
Данный ряд сходится при любом значении 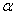 . В условии задачи
. В условии задачи 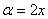
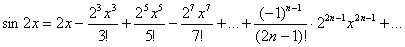
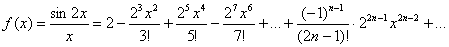
Область сходимости ряда: 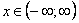 .
.
Пример 8. Разложить функцию 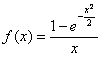 в ряд по степеням
в ряд по степеням 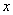 . Найти область сходимости ряда.
. Найти область сходимости ряда.
Решение.
Используем разложение:  . Область сходимости ряда:
. Область сходимости ряда: 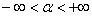 .
.
В данном случае 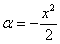
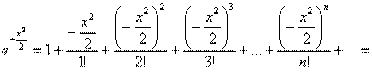
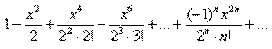
Конструируем функцию дальше:
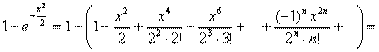
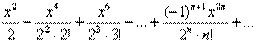
Окончательно:
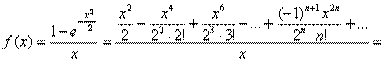
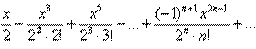
Поскольку разложение сходится при любом α, то область сходимости ряда: 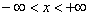
Пример 9. Разложить функцию 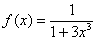 в ряд по степеням
в ряд по степеням 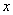 . Найти область сходимости ряда.
. Найти область сходимости ряда.
Решение. Используем частный случай биномиального разложения:
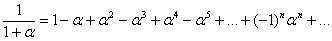
В данном случае 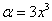 Таким образом:
Таким образом:
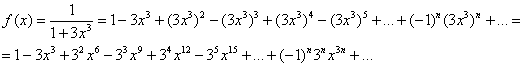
из таблицы находим: «Область сходимости ряда: 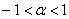 . Сходимость ряда в точках
. Сходимость ряда в точках 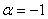 ,
, 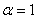 исследуется отдельно». В данном случае
исследуется отдельно». В данном случае 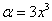 , то есть, ряд точно сходится при:
, то есть, ряд точно сходится при: 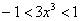 . Делим все части на 3:
. Делим все части на 3: 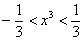 и извлекаем из всех частей кубический корень:
и извлекаем из всех частей кубический корень: 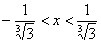 .
.
Подставляем концы интервала в полученный ряд 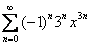 .
.
Если 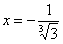 , то:
, то:
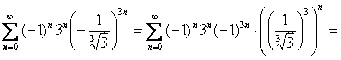
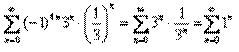
Если 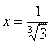 , то
, то 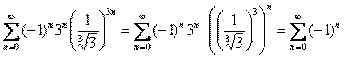
Оба числовых ряда расходятся, так как не выполнен необходимый признак сходимости ряда.
Окончательно. Область сходимости полученного ряда: 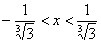
Замечание: Не редкость, когда перед разложением функции в ряд её необходимо предварительно преобразовать. Канонический случай – это разложение функции 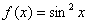 . Перед тем как ее раскладывать в ряд, необходимо понизить степень с помощью известной тригонометрической формулы:
. Перед тем как ее раскладывать в ряд, необходимо понизить степень с помощью известной тригонометрической формулы:  .
.
|
|
|
Пример 10. Разложить функцию 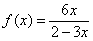 в ряд по степеням
в ряд по степеням 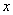 . Найти область сходимости ряда.
. Найти область сходимости ряда.
Решение. Смотрим в таблицу и находим наиболее похожее разложение:
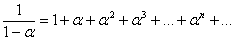
Вверху нужно получить единицу, поэтому представляем функцию в виде оизведения: 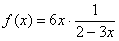
Теперь нам нужно в знаменателе устроить 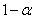 , для этого выносим двойку за скобки:
, для этого выносим двойку за скобки:
 И сокращаем на два:
И сокращаем на два: 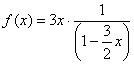
В данном случае 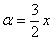 , таким образом:
, таким образом:
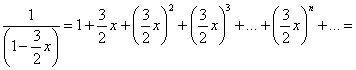
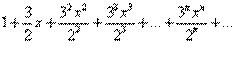
В итоге искомое разложение:
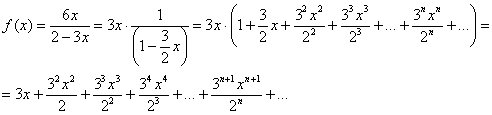
Определим область сходимости ряда. Из таблицы известно, что биномиальный ряд сходится при 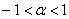 . В данном случае
. В данном случае 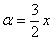 , поэтому:
, поэтому: 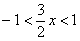
Умножаем все части неравенства на 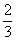 :
: 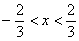 – интервал сходимости полученного ряда.
– интервал сходимости полученного ряда.
Что происходит с рядом 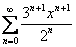 на концах интервала?
на концах интервала?
При 
При 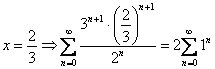
Оба числовых ряда расходятся, так как не выполнен необходимый признак сходимости ряда.
Таким образом, область сходимости полученного ряда: 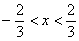
Пример 11. Разложить функцию  в ряд по степеням
в ряд по степеням 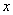 . Найти область сходимости.
. Найти область сходимости.
Решение. Преобразуем функцию: 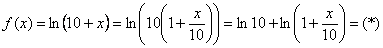
Используем разложение: 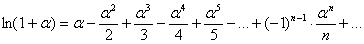
В данном случае 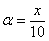
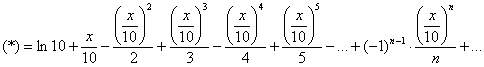
Таким образом:
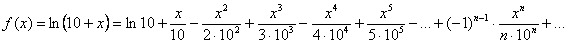
Или короче, в свёрнутом виде: 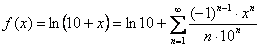
Найдем область сходимости полученного степенного ряда. По таблице находим, что использованное разложение сходится при 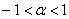 . В данном случае
. В данном случае 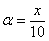 , поэтому:
, поэтому: 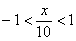
 – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
При 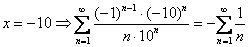 – расходится
– расходится
При 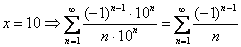 – сходится условно.
– сходится условно.
Таким образом, область сходимости полученного степенного ряда: 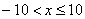
|
|
|
Примеры разложения функций в ряд Тейлора по степеням 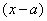
Общая формула Тейлора, о которой уже упоминалось:
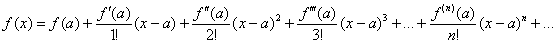
Вместо буквы «а» на практике часто можно встретить букву  .
.
В чём сложность разложения функции по степеням 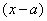 ? Сложность состоит в том, что нам не удастся воспользоваться табличными разложениями, и придётся самостоятельно находить производные.
? Сложность состоит в том, что нам не удастся воспользоваться табличными разложениями, и придётся самостоятельно находить производные.
Пример 12. Разложить функцию 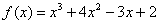 в ряд Тейлора по степеням
в ряд Тейлора по степеням 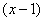
Решение. В данном случае 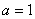 , по формуле Тейлора:
, по формуле Тейлора:

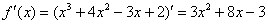
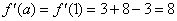
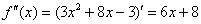
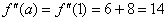
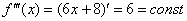
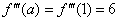
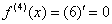 , все производные, начиная с четвёртой производной, будут нулевыми.
, все производные, начиная с четвёртой производной, будут нулевыми.
Теперь подставляем всё в формулу Тейлора:
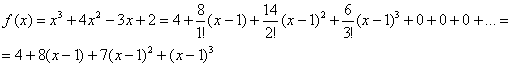
Для проверки можно раскрыть скобки:
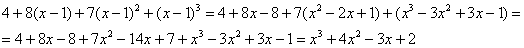
Пример 13. Разложить функцию 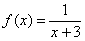 в ряд Тейлора по степеням
в ряд Тейлора по степеням 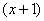 . Найти область сходимости полученного ряда.
. Найти область сходимости полученного ряда.
Решение. Используем разложение функции в ряд Тейлора по степеням 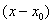
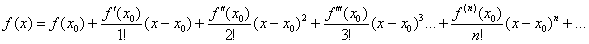
В данном случае: 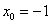
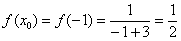

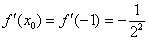
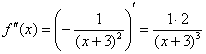
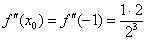
Замечаем, что с такими раскладами производные можно находить до бесконечности. Поэтому необходимо уловить некоторую закономерность. Найдем ещё третью производную:
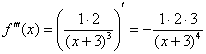
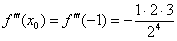
А теперь проанализируем найденные производные:
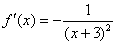 ,
,  ,
, 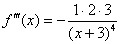 . Закономерность прослеживается: знаки чередуются, в числителе накручивается факториал, а в знаменателе растёт степень.
. Закономерность прослеживается: знаки чередуются, в числителе накручивается факториал, а в знаменателе растёт степень.
Теперь, исходя из выявленной закономерности, нужно составить производную n-порядка. В данном случае она выглядит так: 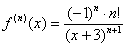
Как проверить, правильно ли составлена энная производная? Подставьте в неё значения 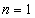 ,
, 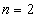 ,
, 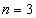 и вас должны получиться в точности первая, вторая и третья производные. После того, как мы убедились в том, что энная производная составлена правильно, подставляем в неё наше значение:
и вас должны получиться в точности первая, вторая и третья производные. После того, как мы убедились в том, что энная производная составлена правильно, подставляем в неё наше значение:
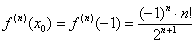
Теперь осталось подставить в формулу Тейлора и аккуратно провести упрощения:
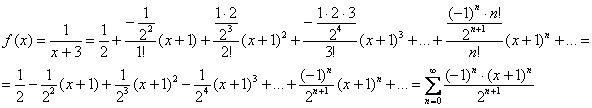
Далее необходимо найти область сходимости полученного степенного ряда 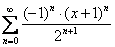 .
.
Область сходимости полученного степенного ряда: 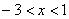
Пример 13. Разложить функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням 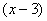 . Найти область сходимости полученного ряда.
. Найти область сходимости полученного ряда.
Решение. Используем разложение функции в ряд Тейлора по степеням 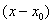 :
:
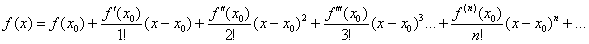
В данном случае:
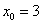
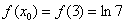
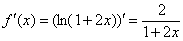
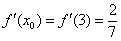
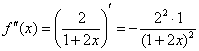
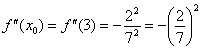
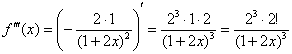

…
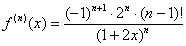
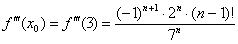
…
Таким образом:
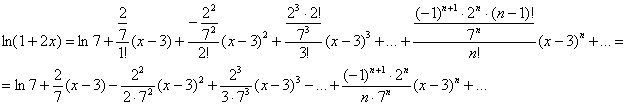
ряд сходится при 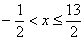 .
.


Дата добавления: 2015-12-21; просмотров: 14; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
