Постановка задачи линейного программирования, геометрический смысл, способы решения производственных задач средствами Microsoft Excel и MathCAD.
Задача линейного программирования (ЛП), состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях. Ограничения накладываются на переменные. Все переменные в любом допустимом решении задачи должны принимать неотрицательные значения.
Геометрический смысл – ограничения представляют собой полуплоскости. Пресеченная полуплоскость даёт область допустимого решения задачи. Оптимальное решение будет находиться на границе области.
Решение в MathCad: given…minimize(..,..),given…maximize(..,..).Этот способ считается приближенным, а поиск решения в Excel основан на симплекс-методе.
Постановка задачи: Предприятие выпускает два вида продукции. Суммарный объем выпуска 40 ед. Выпуск каждого типа должен быть не менее 15 ед. Единица продукции 1-го типа стоит 10, а второго 15. Найти оптимальный выпуск продукции, чтобы был максимальный доход.
Математическая модель: Целевая функция, которую необходимо минимизировать равна 10*х1+15*х2→max. Максимум целевой функции находится при ограничениях: х1+х2=40; х1≥15; х2≥15; х1≥0; х2≥0.
Многошаговые задачи принятия решений. Формулировка задачи динамического программирования. Метод динамического программирования. Принцип оптимальности Беллмана. Решение динамических задач методом динамического программирования.
Пусть рассматривается задача распадающегося на m этапов. Показатель эффективности задачи в целом обозначается через W, а показатель эф-ти на шагах через φi и изменяется 1,m. Соответствующие данные можно связать.
|
|
|
Эф-ть всей задачи будет состоять из суммы эффективности на каждом шаге: W=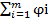 
(1).
Динамическое программирование – это метод оптимизации многошаговых процессов критерий эффективности который обладает св-ом (1).
В задачах ДП критерий эффективности называется выигрышем. Переменная xi от которой зависти выигрыш на i-ом шаге называется шаговым управлением. Управлением процесса в целом X наз-ся последовательностью шаговых управлений: (x1 , x2 ,..., xk ,..., xn ), число которых и определяет количество шагов задачи. Задача оптимизации формулируется как конечный многошаговый процесс управления; целевая функция (выигрыш) является аддитивной и равна сумме целевых функций каждого шага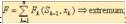 
выбор управления xk на каждом шаге зависит только от состояния системы k этому шагу Sk-1, и не влияет на предшествующие шаги (нет обратной связи); состояние системы Sk после каждого шага управления зависит только от предшествующего состояния системы Sk-1 и этого управляющего воздействия xh (отсутствие последействия) и может быть записано в виде уравнения состояния: Sk = fk(Sk-1 , xk), k = 1, n; на каждом шаге управление xk зависит от конечного числа управляющих переменных, а состояние системы зависит Sk – от конечного числа параметров;
|
|
|
Дата добавления: 2015-12-17; просмотров: 15; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!